Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение заданий 6. ЕГЭ 2017. Математика, И.В. Ященко. 36 вариантов
Содержание
- 1. Решение заданий 6. ЕГЭ 2017. Математика, И.В. Ященко. 36 вариантов
- 2. Вариант 1. В четырёхугольник ABCD вписана
- 3. Вариант 1. В четырёхугольник ABCD вписана
- 4. Вариант 2. Задание 6. В четырёхугольник
- 5. Вариант 2. Задание 6. В четырёхугольник
- 6. Вариант 3. Задание 6. В
- 7. Вариант 3. Задание 6. В
- 8. Вариант 4.
- 9. Вариант 4.
- 10. Вариант 5.
- 11. Вариант 5.
- 12. Вариант 6.
- 13. Вариант 6.
- 14. Вариант 7.
- 15. Вариант 7. Задание 6. Угол АСО
- 16. Вариант 8. Задание 6. Через концы
- 17. Вариант 8. Задание 6. Через концы
- 18. Вариант 9. Задание 6.
- 19. Вариант 9. Задание 6.
- 20. Вариант 10. Задание 6.
- 21. Вариант 10. Задание 6.
- 22. Скачать презентанцию
Слайды и текст этой презентации
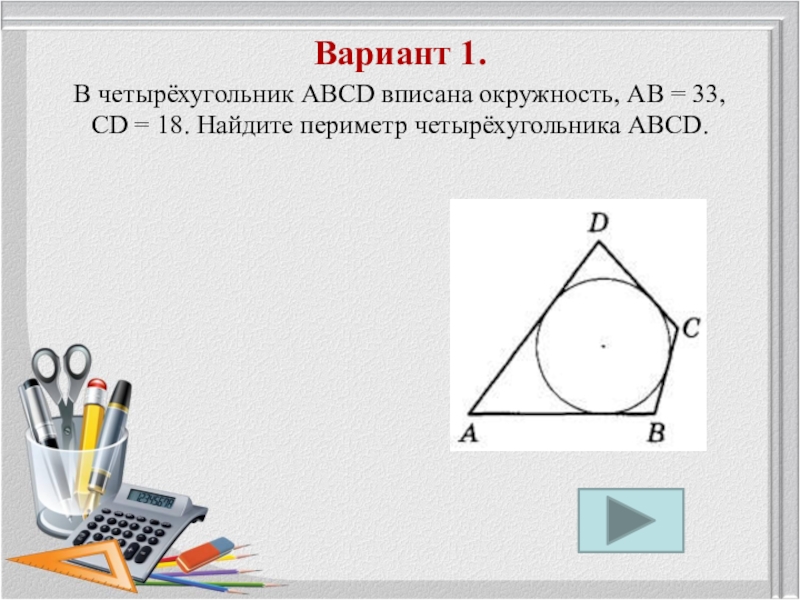
Слайд 2Вариант 1. В четырёхугольник ABCD вписана окружность, АВ = 33,
CD = 18. Найдите периметр четырёхугольника ABCD.
Слайд 3Вариант 1. В четырёхугольник ABCD вписана окружность, АВ = 33,
CD = 18. Найдите периметр четырёхугольника ABCD.
Решение.
В любом описанном четырёхугольнике
суммы противоположных сторон равны.AD+BC=AB+CD.
По условию задачи нам даны длины сторон AB=33 и CD=18, следовательно,
AD+BC=33+18=51
Периметр четырехугольника – это сумма длин всех его сторон, то есть
P=AD+BC+AB+CD,
и, подставляя известные числовые значения, имеем:
P=51+51=102.
Ответ: 102.
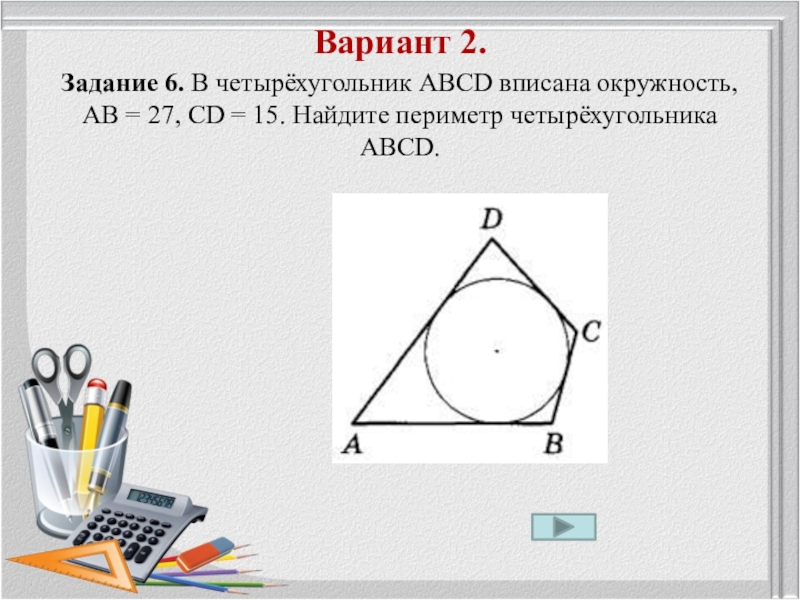
Слайд 4 Вариант 2. Задание 6. В четырёхугольник ABCD вписана окружность, АВ =
27, CD = 15. Найдите периметр четырёхугольника ABCD.
Слайд 5 Вариант 2. Задание 6. В четырёхугольник ABCD вписана окружность, АВ =
27, CD = 15. Найдите периметр четырёхугольника ABCD.
Решение.
В любом описанном
четырёхугольнике суммы противоположных сторон равны.AD+BC=AB+CD.
По условию задачи нам даны длины сторон AB=27 и CD=15, следовательно,
AD+BC=27+15=42
Периметр четырехугольника – это сумма длин всех его сторон, то есть
P=AD+BC+AB+CD,
и, подставляя известные числовые значения, имеем:
P=42+42=84.
Ответ: 84.
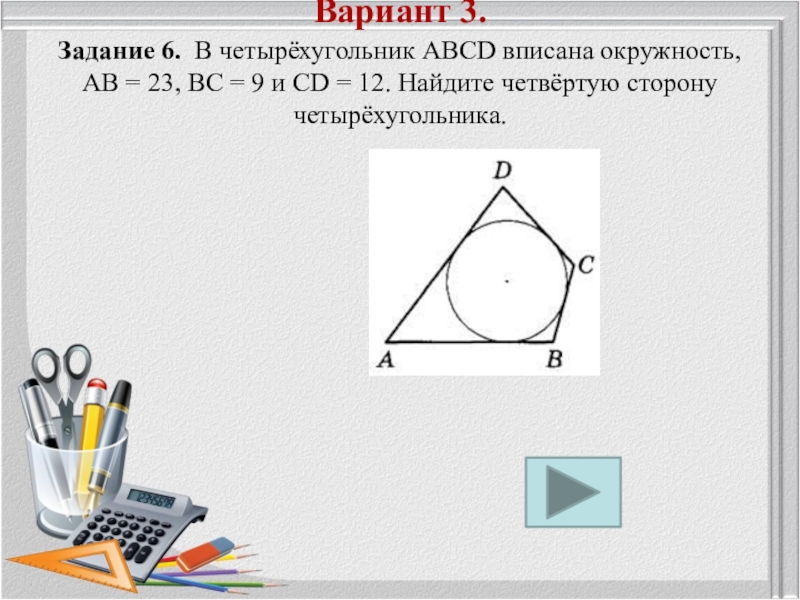
Слайд 6 Вариант 3. Задание 6. В четырёхугольник ABCD вписана окружность, АВ
= 23, ВС = 9 и СD = 12. Найдите
четвёртую сторону четырёхугольника.Слайд 7 Вариант 3. Задание 6. В четырёхугольник ABCD вписана окружность, АВ
= 23, ВС = 9 и СD = 12. Найдите
четвёртую сторону четырёхугольника.Решение.
В любом описанном четырёхугольнике суммы противоположных сторон равны.
AD+BC=AB+CD.
По условию задачи нам даны длины сторон AB=23 и CD=12, следовательно,
AD+BC=23+12=35
AD=35-9=26
Ответ: 26.
Слайд 8 Вариант 4. Задание 6. В четырёхугольник ABCD вписана окружность, АВ
= 18, ВС = 12 и CD = 13. Найдите
четвёртую сторону четырёхугольника.Слайд 9 Вариант 4. Задание 6. В четырёхугольник ABCD вписана окружность, АВ
= 18, ВС = 12 и CD = 13. Найдите
четвёртую сторону четырёхугольника.Решение.
В любом описанном четырёхугольнике суммы противоположных сторон равны.
AD+BC=AB+CD.
По условию задачи нам даны длины сторон AB=18 и CD=13, следовательно,
AD+BC=18+13=31
AD=31-12=19
Ответ: 19.
Слайд 10 Вариант 5. Задание 6. Отрезки АС и BD — диаметры
окружности с центром О. Угол АСВ равен 44°. Найдите угол
AOD. Ответ дайте в градусах.Слайд 11 Вариант 5. Задание 6. Отрезки АС и BD — диаметры
окружности с центром О. Угол АСВ равен 44°. Найдите угол
AOD. Ответ дайте в градусах.
Слайд 12 Вариант 6. Задание 6. Отрезки АС и BD — диаметры
окружности с центром О. Угол ACB равен 50°. Найдите угол
AOD. Ответ дайте в градусах.Слайд 13 Вариант 6. Задание 6. Отрезки АС и BD — диаметры
окружности с центром О. Угол ACB равен 50°. Найдите угол
AOD. Ответ дайте в градусах.
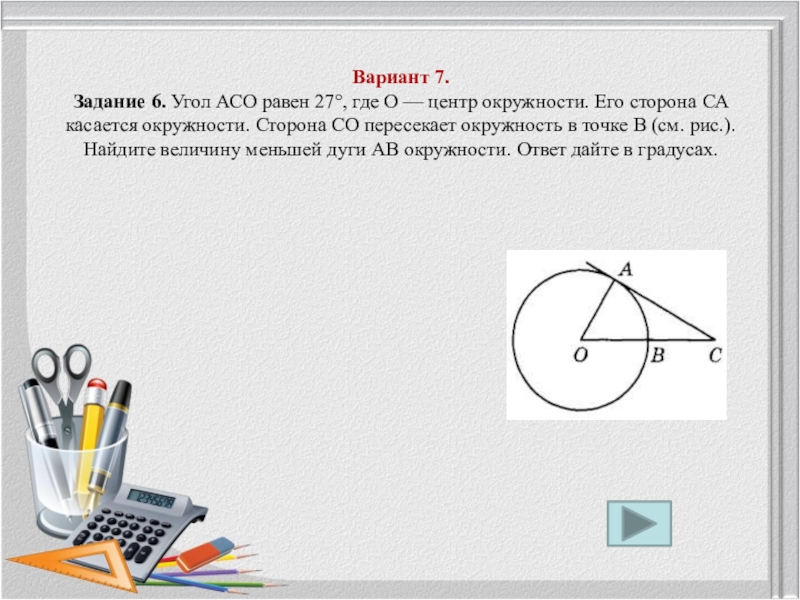
Слайд 14 Вариант 7. Задание 6. Угол АСО равен 27°, где О
— центр окружности. Его сторона СА касается окружности. Сторона СО
пересекает окружность в точке В (см. рис.). Найдите величину меньшей дуги АВ окружности. Ответ дайте в градусах.Слайд 15Вариант 7. Задание 6. Угол АСО равен 27°, где О
— центр окружности. Его сторона СА касается окружности. Сторона СО
пересекает окружность в точке В (см. рис.). Найдите величину меньшей дуги АВ окружности. Ответ дайте в градусах.Решение.
Градусная мера меньшей дуги AB будет равна центральному углу AOB. Найдем этот угол. Так как отрезок AC является касательной к окружности, а отрезок AO – радиус окружности, то угол OAC – прямой и равен 90°. Учитывая, что сумма углов в треугольнике 180°, найдем угол AOB:
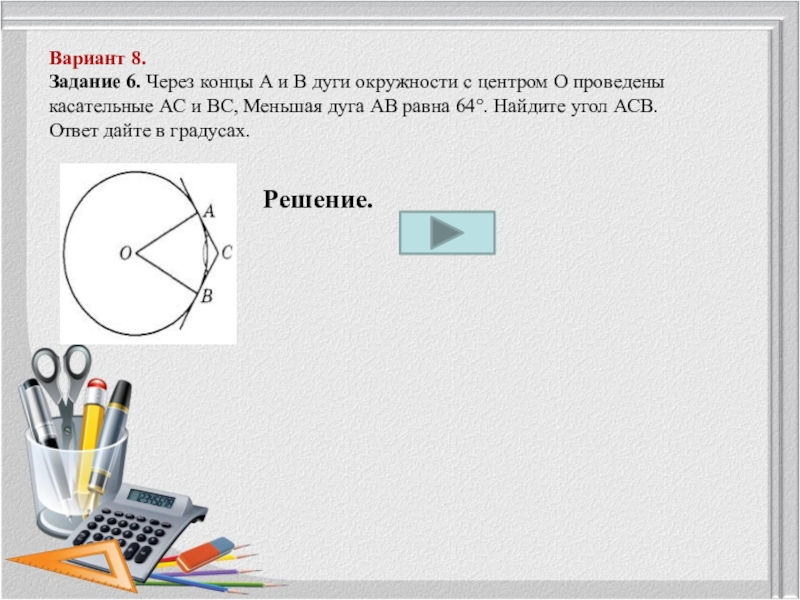
Слайд 16Вариант 8. Задание 6. Через концы А и В дуги
окружности с центром О проведены касательные АС и ВС, Меньшая
дуга АВ равна 64°. Найдите угол АСВ. Ответ дайте в градусах.Решение.
Слайд 17Вариант 8. Задание 6. Через концы А и В дуги
окружности с центром О проведены касательные АС и ВС, Меньшая
дуга АВ равна 64°. Найдите угол АСВ. Ответ дайте в градусах.Решение.
Так как AC и BC – касательные, а OA и OB – радиусы окружности, то углы OAB и OBC – прямые и равны 90°. На меньшую дугу AB опирается центральный угол AOB, следовательно, градусная мера угла AOB равна градусной мере дуги AB в 64°. Имеем четырехугольник OABC, в котором известны три угла, а сумма всех углов в четырёхугольнике равна 360°. Отсюда вычисляем последний неизвестный угол ACB:
Слайд 18Вариант 9.
Задание 6.
Решение.
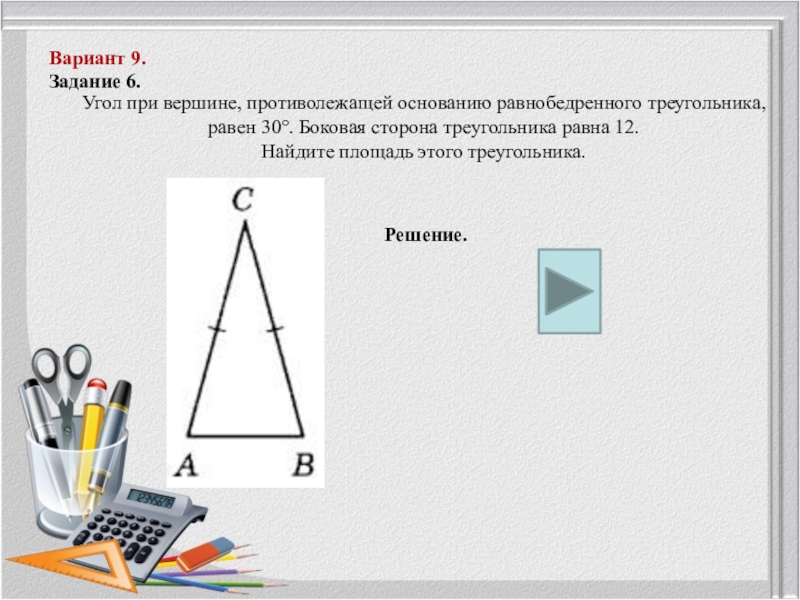
Угол при вершине, противолежащей основанию
равнобедренного треугольника,
равен 30°. Боковая сторона треугольника равна 12.
Найдите
площадь этого треугольника.Слайд 19Вариант 9.
Задание 6.
Решение.
Теорема.
Площадь треугольника равна
Половине
произведения двух его сторон на
синус угла между ними.
Вычислим площадь треугольника
через две стороны и угол между ними:S=0,5*AC*CB*sin
.
Ответ: 36.
Угол при вершине, противолежащей основанию равнобедренного треугольника,
равен 30°. Боковая сторона треугольника равна 12.
Найдите площадь этого треугольника.
Слайд 20Вариант 10.
Задание 6.
Решение.
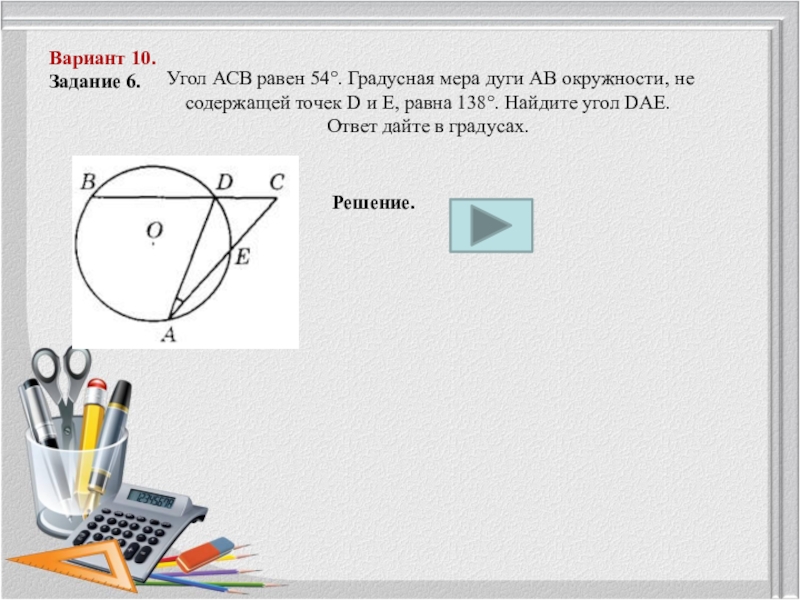
Угол АСВ равен 54°. Градусная
мера дуги АВ окружности, не
содержащей точек D и Е,
равна 138°. Найдите угол DAE. Ответ дайте в градусах.
Слайд 21Вариант 10.
Задание 6.
Решение.
Вычислим < BDA, < BDA
- вписанный в окружность и опирается на дугу AB. Так
как вписанный вписанный угол измеряется половиной дуги АВ, то его градусная мера будет в 2 раза меньше градусной меры дуги AB. < BDA = 138/2 = 69°. Рассмотрим теперь < ADC, который является смежным к углу BDA, следовательноИз рисунка видно, что углы DAC и DAE равны между собой, получаем < DAE =180° - 111° - 54°= 15°.
Ответ: 15
Угол АСВ равен 54°. Градусная мера дуги АВ окружности, не
содержащей точек D и Е, равна 138°. Найдите угол DAE.
Ответ дайте в градусах.