Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Российский государственный университет им. И. Канта Математический
Содержание
- 1. Российский государственный университет им. И. Канта Математический
- 2. Предыстория исследования операций 1) Работы Ланчестера по
- 3. История развития методов и средств исследования операцийЗарождение
- 4. История развития методов и средств исследования операцийВ
- 5. История развития методов и средств исследования операцийВ
- 6. История развития методов и средств исследования операцийВ
- 7. История развития методов и средств исследования операцийНаучная
- 8. История развития методов и средств исследования операцийНаучная
- 9. История развития методов и средств исследования операцийНаучная
- 10. История развития методов и средств исследования операцийНаучная
- 11. История развития методов и средств исследования операцийНаучная
- 12. История развития методов и средств исследования операцийНаучная
- 13. История развития методов и средств исследования операцийНаучная
- 14. История развития методов и средств исследования операцийНаучная
- 15. Предмет и задачи исследования операцийПод исследованием операций
- 16. Предмет и задачи исследования операцийПредмет исследования операций -
- 17. Принципы исследования операций1. Системный подход к анализу
- 18. Ситуация 1Ситуация 2Ситуация 3Лицо, принимающее решенияМорской рыбный
- 19. Если состояние порта таково, что он простаивает
- 20. Впервые ЛПР задумается над ситуацией 3. Число
- 21. Оптимизационные задачи в науке и технике и
- 22. Цель - желаемое состояние объекта в будущем.Целеполагание -
- 23. Элементы решения - параметры, совокупность которых образует
- 24. Ограничения (дисциплинирующие условия) – пределы в которых
- 25. 1. План снабжения предприятий. Задача операции -
- 26. Принятие решенийПринятие решений – особый вид целенаправленной
- 27. Модель процесса принятия решений О.С. Виханского и
- 28. Модель коллективного принятия решений М.В. Самсоновой и
- 29. Индивидуальные решения
- 30. Автор графика – Михай Чиксентмихайи, профессор психологии
- 31. Первую просили принимать решение немедленно, не думая.
- 32. Закон Йеркса - Додсона (Yerkes-Dodson)- психологический закон,
- 33. Коллективные решенияСистемы поддержки принятия решенийСитуационные комнаты Ситуационные центры
- 34. Формальная модель задачи принятия решенийЗадача принятия решений
- 35. Линейное программирование Задачи линейного программированияПостановка задачи линейного
- 36. Линейное программированиеГеометрический смысл задачи линейного программированияЗадача (модель)
- 37. Шаг 2. Построение целевой функции.Логично предположить, что
- 38. Шаг 3. Определение ограничений.Ограничения должны учитывать возможности
- 39. Поскольку ежедневный расход сырья М1 и М2
- 40. Окончательно задача будет записана следующим образом:При выполнении
- 41. Поиск оптимального решенияКак найти оптимальное допустимое решение,
- 42. 112345623456AFEDCB154236Область допустимых решений123456Область допустимых решений
- 43. Графический способ решения задач линейного программированияСлучай максимизации
- 44. Оптимум:Максимизироватьz = 10z = 15z = 2112Графический
- 45. Графический способ решения задач линейного программированияСлучай максимизации
- 46. Графический способ решения задач линейного программированияСлучай максимизации
- 47. Линейное программирование Задачи линейного программированияНахождение минимума целевой
- 48. Задачи линейного программированияНахождение минимума целевой функцииОпределяем переменные.
- 49. Задачи линейного программированияНахождение минимума целевой функцииВведем ограничения.
- 50. Нахождение минимума целевой функцииПри выполнении ограничений:Окончательно модель примет следующий вид:
- 51. Область допустимых решений
- 52. Графический анализ чувствительностиМодель ЛП – «моментальный снимок»
- 53. Графический анализ чувствительностиИзменение коэффициентов переменных в целевой функции
- 54. Графический анализ чувствительностиИзменение коэффициентов переменных в целевой функцииОбщий вид целевой функции задачи ЛП с двумя переменными:
- 55. Слайд 55
- 56. Графический анализ чувствительностиИзменение коэффициентов переменных в целевой функции
- 57. Слайд 57
- 58. Слайд 58
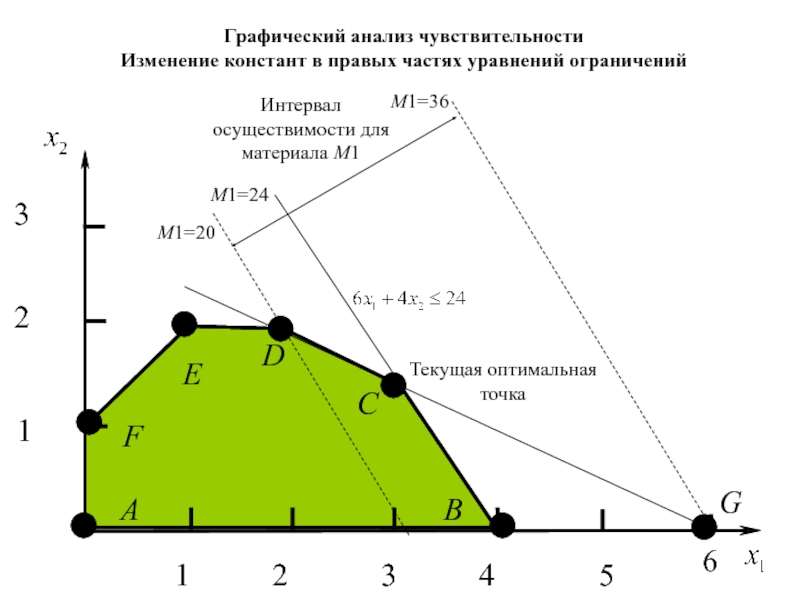
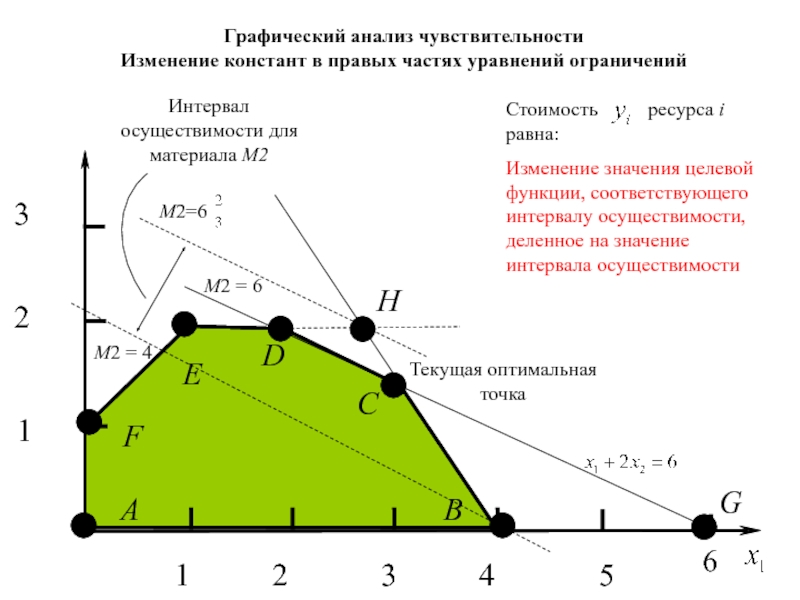
- 59. Графический анализ чувствительностиИзменение значений констант в правых
- 60. Стоимость ресурса i
- 61. Слайд 61
- 62. Симплекс-метод решения задач линейного программированияГрафический способ решения
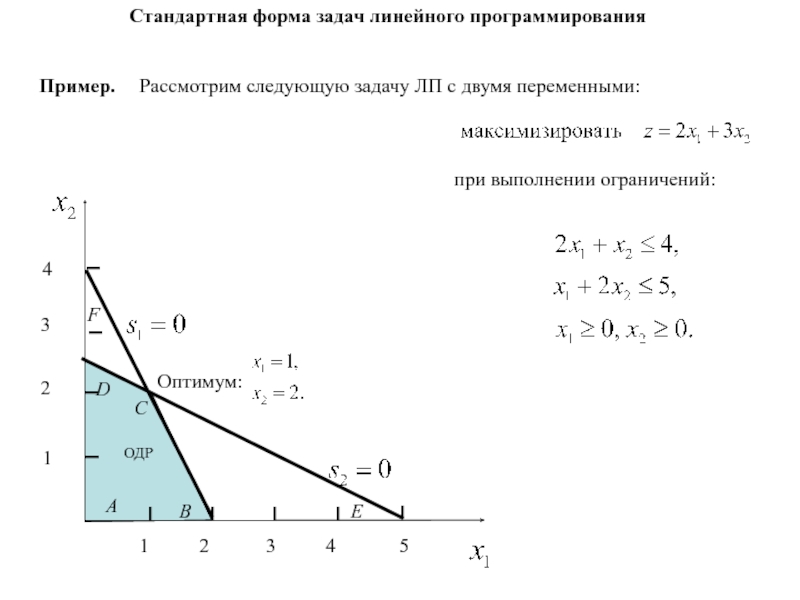
- 63. Стандартная форма задач линейного программированияЧтобы перейти к
- 64. Преобразование неравенств в равенства
- 65. Преобразование неравенств в равенстваПреобразование правой части к
- 66. Пример.Рассмотрим следующую задачу ЛП с двумя переменными:112342345AFEDCBОДРОптимум:Стандартная форма задач линейного программирования
- 67. Преобразуем задачу ЛП к стандартной форме:Стандартная форма задач линейного программированияПример
- 68. Как определить: какие n - m переменные
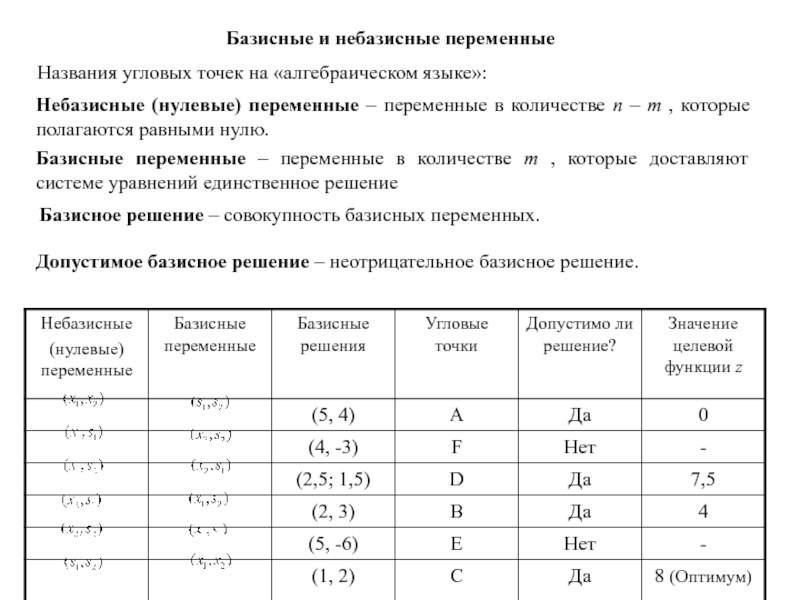
- 69. Базисные и небазисные переменныеНазвания угловых точек на
- 70. Размерность задач ЛППри возрастании размера задачи (при
- 71. Слайд 71
- 72. Алгоритм симплекс-методаОба пути A→ B → C
- 73. Перевод небазисных переменных в базисные и наоборот
- 74. При выполнении ограничений:Алгоритм симплекс-методаРассмотрим алгоритм симплекс-метода на
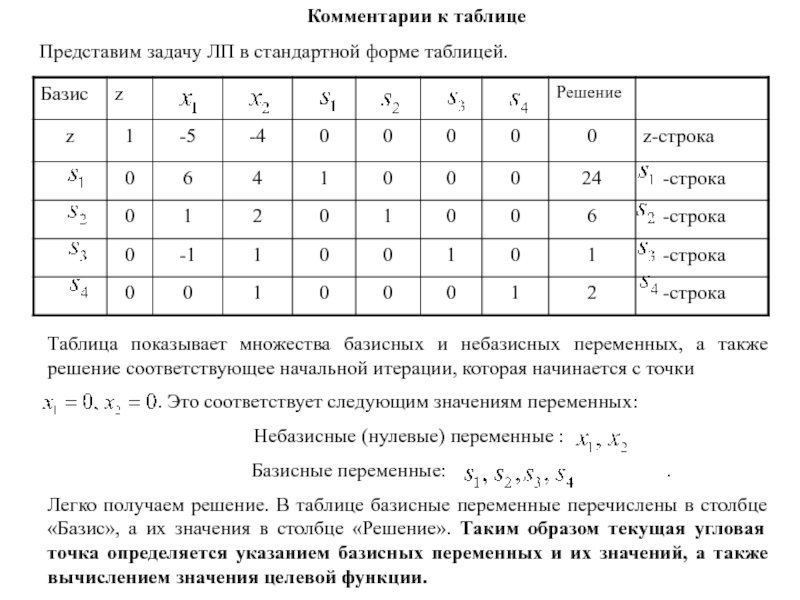
- 75. Комментарии к таблицеПредставим задачу ЛП в стандартной форме таблицей.
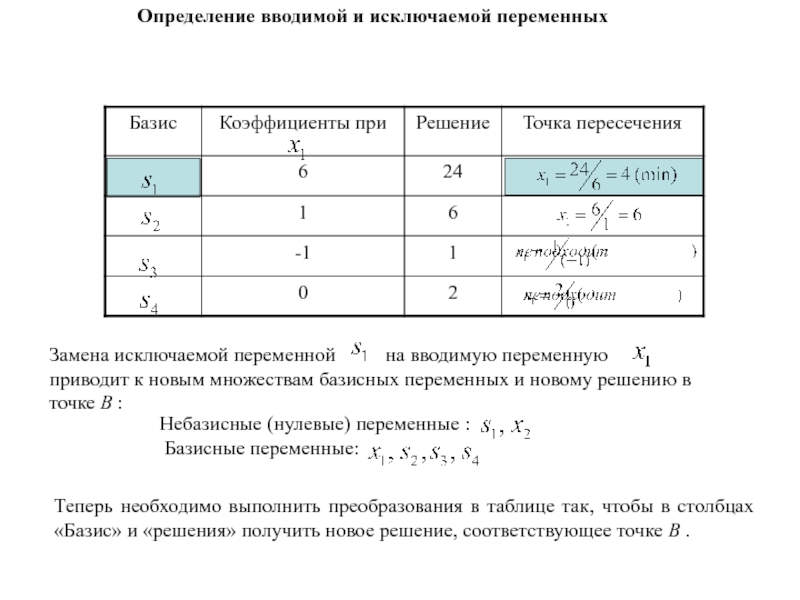
- 76. Определение вводимой и исключаемой переменныхОпределение вводимой переменной.
- 77. Определение вводимой и исключаемой переменных
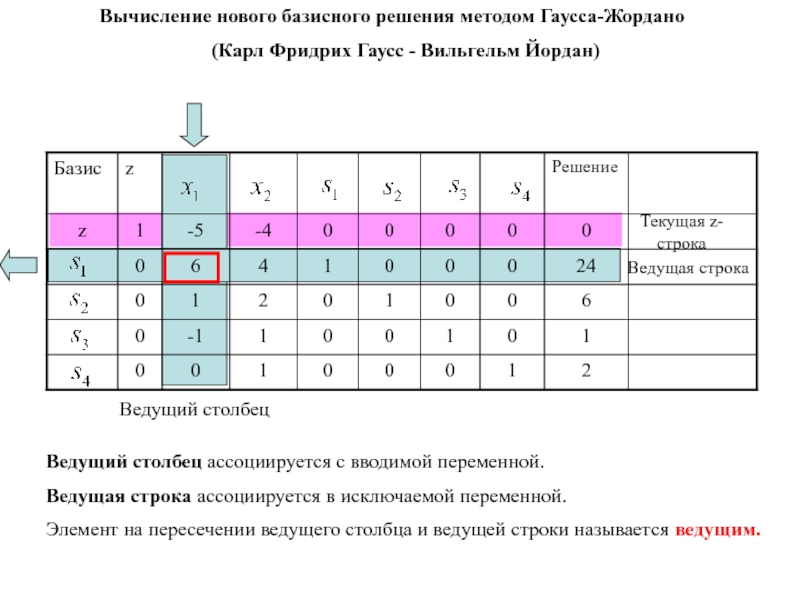
- 78. Вычисление нового базисного решения методом Гаусса-Жордано(Карл Фридрих
- 79. Вычисление нового базисного решения методом Гаусса-ЖорданоПроцесс вычисления
- 80. Ведущий столбецВедущая строкаВедущий столбецВедущая строкаТекущая z- строкаНовая ведущая строкаНовая z- строка
- 81. Процесс вычисления базисного решения состоит из двух
- 82. Теперь необходимо выполнить преобразования в таблице так,
- 83. Вычисление нового базисного решения методом Гаусса-ЖорданоПоскольку z-строка
- 84. Явления вычислительного процесса симплекс-методаВырожденность. Проверка условия допустимости
- 85. Явления вычислительного процесса симплекс-метода ВырожденностьИнформация, что некоторые
- 86. Явления вычислительного процесса симплекс-метода Альтернативные оптимальные решенияАльтернативные
- 87. Явления вычислительного процесса симплекс-метода Неограниченная целевая функцияНеограниченная
- 88. Явления вычислительного процесса симплекс-метода Отсутствие допустимых решенийОтсутствие
- 89. Двойственность задач линейного программированияИсходную задачу ЛП будем
- 90. Правила преобразования прямой в двойственную задачуПеременные и
- 91. j – ое ограничения 2-задачиКоэффициенты целевой функции 2-задачиПреобразование прямой в двойственную задачу
- 92. Правила определения типа оптимизации и типа ограниченийПрямая задачаДвойственная задачаmaxminminmax
- 93. Прямая задачаМаксимизироватьПри ограниченияхПрямая задача в стандартной формеМаксимизироватьПри ограниченияхДвойственные переменныеДвойственная задачаПри ограниченияхМинимизироватьПример прямой и двойственной задачи(избыточное условие)
- 94. Соотношения между прямой и двойственной задачами ЛПДвойственной
- 95. Экономическая интерпретация двойственностиДля любой пары допустимых решений
- 96. Экономическая интерпретация двойственности
- 97. Нелинейное программирование
- 98. Методы решения задач нелинейного программированияГеометрический методМетод множителей ЛагранжаМетод штрафных функцийГенетические алгоритмы
- 99. Решение задач нелинейного программирования
- 100. Найти максимальное значение функции:при условиях:Пример задачи НЛП
- 101. 241232468101214681012DBGCОДР123A44
- 102. Слайд 102
- 103. Метод множителей Лагранжа
- 104. Рассмотрим задачу: f (X) max ,
- 105. Идею решения задачи Лагранжа можно представить следующим
- 106. Метод множителей Лагранжа
- 107. Решив систему уравнений, получим все точки
- 108. Метод множителей ЛагранжаПример
- 109. Метод множителей ЛагранжаПример геометрического решения
- 110. Слайд 110
- 111. Метод множителей ЛагранжаПример решения метод множителей Лагранжа
- 112. Метод штрафных функций
- 113. Штрафная функция обычно имеет вид:гдеа
- 114. Используя штрафную функцию, последовательно переходят от одной
- 115. Геометрически направление градиента функции совпадает с направлением
- 116. Найдем градиент функции
- 117. Последовательность выполнения этапов метода штрафных функций:Определяют исходное
- 118. Пример Найти максимальное значение функции:При условиях:Построим ОДР
- 119. Метод штрафных функцийПример Область допустимых решений и
- 120. Пример Метод штрафных функций
- 121. Пример Метод штрафных функций
- 122. Метод штрафных функций
- 123. Пример Метод штрафных функций
- 124. Пример Метод штрафных функций
- 125. Пример Метод штрафных функций
- 126. Сравнивая значения целевой функции, найденные в точках
- 127. Динамическое программированиеСловосочетание динамическое программирование впервые было использовано
- 128. Динамическое программированиеДинамическое программирование (ДП) определяет оптимальное решение
- 129. Динамическое программированиеПонятия декомпозиции и редукцииДекомпозиция — научный метод,
- 130. Динамическое программированиеЗадача о кратчайшем путиНеобходимо выбрать кратчайший
- 131. Динамическое программированиеЗадача о кратчайшем путиДля решения задачи
- 132. Динамическое программированиеЗадача о кратчайшем путиОбщая задача состоит
- 133. Динамическое программированиеЗадача о кратчайшем путиЭтап 2. Итоговые
- 134. Определим города, через которые проходит кратчайший маршрут.
- 135. Динамическое программированиеЗадача о кратчайшем пути
- 136. Динамическое программированиеВ действительности состояние системы на этапе
- 137. Рассмотренный выше пример, когда вычисления выполнялись последовательно,
- 138. Этап 3. Поскольку узел 7
- 139. Этап 2. Так как маршрута (2,6) не
- 140. Этап 1. Из вершины 1 начинаются три
- 141. Безусловная оптимизацияПоиск экстремумов функций в условиях отсутствия
- 142. abОсновные понятия экстремальных задач без ограничений
- 143. Методы оптимизацииМетоды одномерной оптимизацииМетоды безусловной оптимизацииМетоды условной оптимизацииМетоды моделирования эволюцииМетоды оптимизацииМетоды имитирующие интеллект роя
- 144. Методы одномерной оптимизацииМетод дихотомического поискаМетод золотого сеченияМетод чисел Фибоначчи Метод полиномиальной аппроксимации
- 145. Методы безусловной оптимизацииМетод наискорейшего спускаМетод РозенблокаМетод конфигурацийМетод
- 146. Методы моделирования эволюцииКлассические генетические алгоритмыГенетические микроалгоритмыГенетические алгоритмы со взаимной эволюциейПараллельные эволюционные алгоритмыГенетические алгоритмы для многокритериальной оптимизации
- 147. Методы имитирующие интеллект роя1. Муравьиный алгоритм (англ. Ant
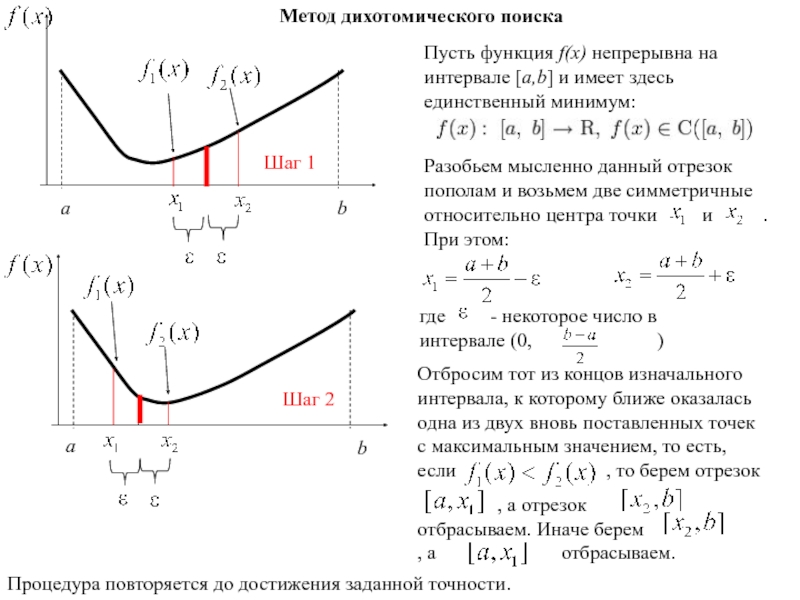
- 148. Метод дихотомического поискаПроцедура повторяется до достижения заданной точности.
- 149. Слайд 149
- 150. Пример наискорейшего спускаМетод наискорейшего спуска может иметь
- 151. Классические генетические алгоритмыГенетические алгоритмы (ГА) своим существованием
- 152. Ученых заинтересовали признаки естественной эволюции, а точнее
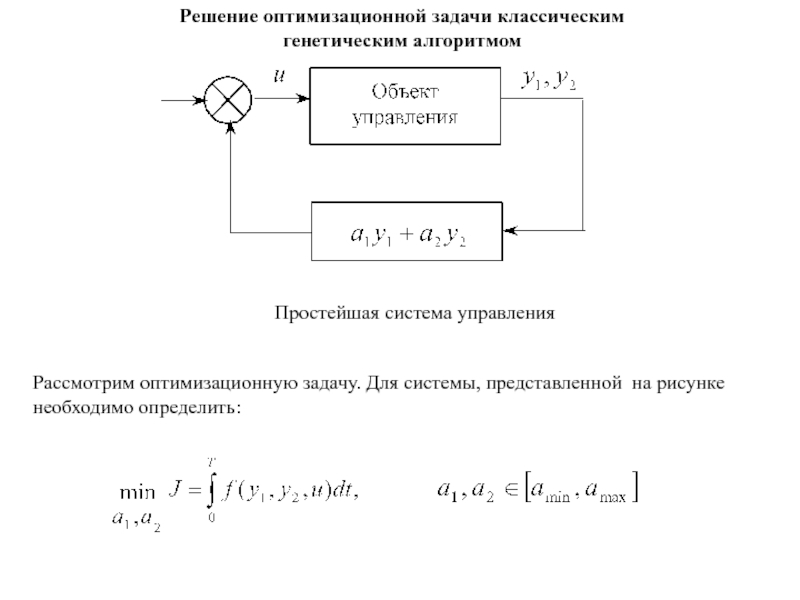
- 153. Рассмотрим оптимизационную задачу. Для системы, представленной на
- 154. Параметры этой задачи -
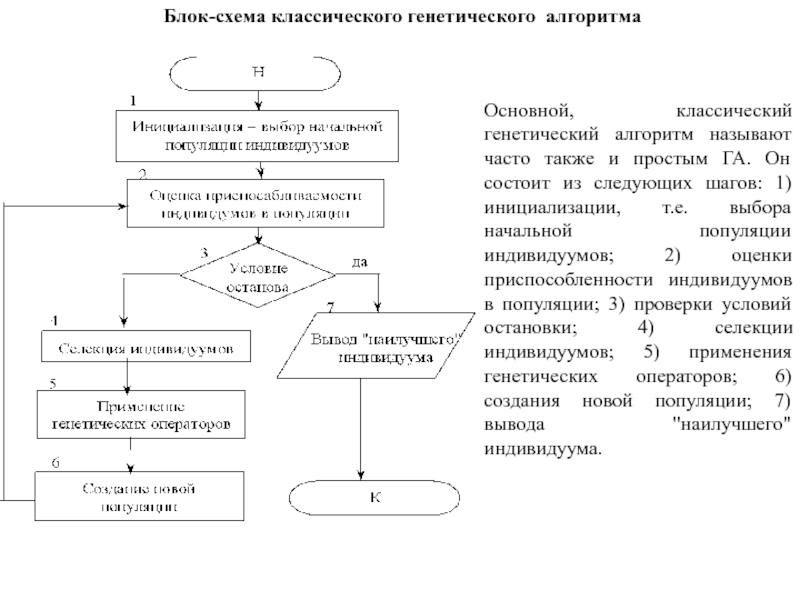
- 155. Основной, классический генетический алгоритм называют часто также
- 156. Инициализация - создание начальной популяции. Основано на
- 157. Селекция индивидуумов. Основана на выборе, по значениям
- 158. Выбор индивидуума - следствие оборота колеса рулетки.
- 159. Применение генетических операторов. Применение генетических операторов к
- 160. Оператор скрещивания. Первый этап скрещивания - выбор
- 161. Оператор мутации. В соответствии с вероятностью мутации,
- 162. Возьмем упрощенный и немного искусственный пример, нахождения
- 163. Оценка приспосабливаемости индивидуумов в популяции. Значения функции
- 164. Селекция. Выполним селекцию методом рулетки. Для каждой
- 165. Применение генетических операторов. Предположим, что множество индивидуумов,
- 166. Создание новой популяции. После скрещивания имеем следующую
- 167. Работа генетического алгоритма над задачей безусловной оптимизации
- 168. Основы теории массового обслуживанияБольшинство систем, с которыми
- 169. Пример 1. Телефонная связь времен Эрланга представляла из
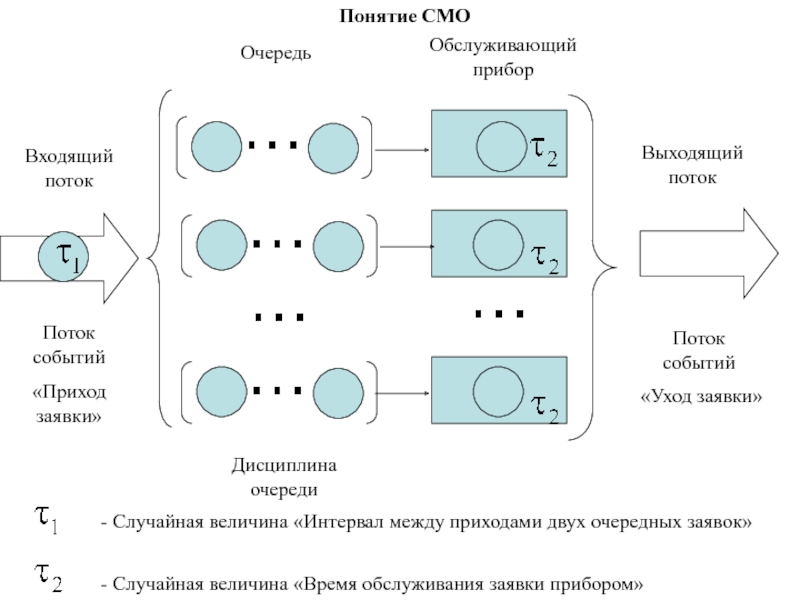
- 170. - Случайная величина «Интервал между приходами двух очередных заявок»- Случайная величина «Время обслуживания заявки прибором»Понятие СМО
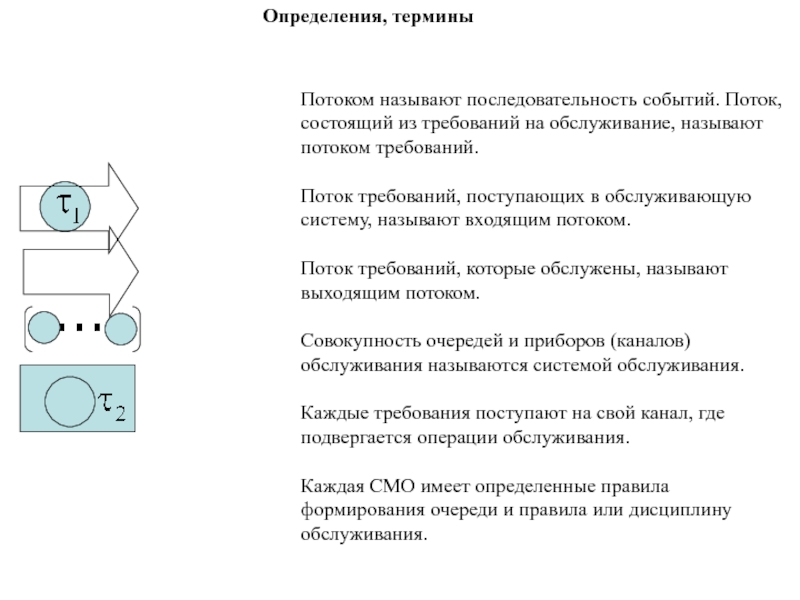
- 171. Потоком называют последовательность событий. Поток, состоящий из
- 172. СМО различают:По дисциплине обслуживания:обслуживание в порядке поступления;обслуживание
- 173. Основная задача ТМО - установление зависимости между
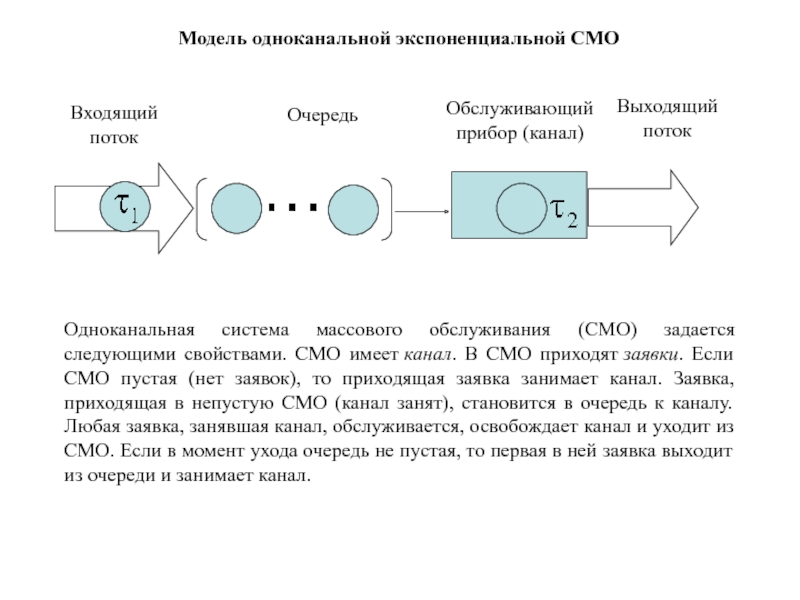
- 174. Входящий потокВыходящий потокОчередьОбслуживающий прибор (канал)Модель одноканальной экспоненциальной
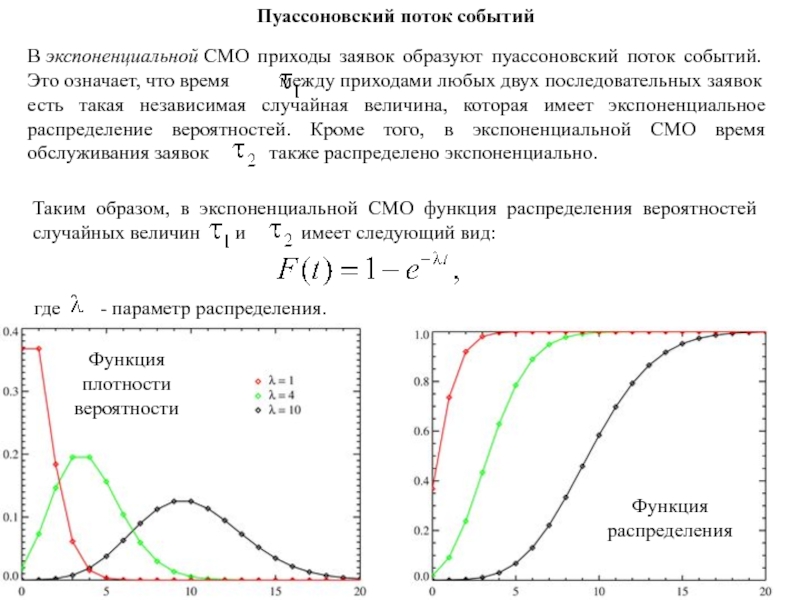
- 175. Функция плотности вероятностиФункция распределенияПуассоновский поток событий
- 176. Цель анализа СМО заключается в расчете ее
- 177. Коэффициент загрузки рассчитывается по формуле: Если выполняется условие ρ
- 178. В стационарном режиме среднее число M заявок в СМО постоянно. Поэтому
- 179. Коэффициент загрузки ρ в стационарном режиме можно интерпретировать следующими
- 180. Формула Литтла
- 181. Применяя формулу Литтла к очереди в СМО,
- 182. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Российский государственный университет им. И. Канта Математический факультет
Кафедра компьютерного
моделирования и информационных систем
2010Слайд 2Предыстория исследования операций
1) Работы Ланчестера по моделированию боевых операций
(1916 г.).
2) Работы по теории массового обслуживания Эрланга,
нашедшие практическую реализацию в начале двадцатого столетия в Копенгагене. 3) Исследования Левинсона в области розничной торговли в начале 20-х годов.
Слайд 3История развития методов и средств исследования операций
Зарождение исследования операций связано
концепцией индустриального общества и с разработкой английскими военно-воздушными силами систем
управления (1936 – 1937 гг.): 1) системы обнаружения и слежения за одиночным атакующим самолетом противника («Бодси») и 2) системы сопровождения и наведения взаимодействующих истребителей военно-воздушных сил обороны («Биггин Хилл»).Цель проектов - обеспечить согласованные действий участников боевых операций: людей и технических средств.
Выработка оценок эффективности разрабатываемых операций получила название «операционное исследование».
В 1942 г. работы по исследованию военных операций начались в США.
Слайд 4История развития методов и средств исследования операций
В 1945 – 1950
гг. работы по исследованию операций в военной области в Англии,
США и Канаде были продолжены еще в более широком масштабе. Центр исследований сместился в авиационную промышленность.В 1965 – 1975 гг. наблюдалось расширение сферы применения исследования операций в новых направлениях: охране общественного порядка, транспорте, управлении ростом и развитием городов, жилищном строительстве, здравоохранении, образовании и социальных услугах.
Слайд 5История развития методов и средств исследования операций
В 1965 г. американский
социолог и политолог Д. Белл выдвинул концепцию постиндустриального общества. Он
обосновал переход общественных отношений от индустриального общества (рационального использования ресурсов) к постиндустриальному (рационального использования информации и знаний). К 1975 г. стали актуальны профессиональные знания и опыт специалистов, решающих широкий круг практических, творческих, интеллектуальных задач.В 1955 г. появился термин «Искусственный интеллект». В 1969 г. появилась первая экспертная система (система, использующая профессиональные знания специалиста для рассуждений над решением задачи). С 1980 г. методы искусственного интеллекта превратились в индустрию.
Слайд 6История развития методов и средств исследования операций
В эпоху разработки компьютерной техники
возник системный анализ (А.А. Богданов, Л. Берталанфи, Н.Винер, Н.Н. Моисеев,
Э. Эшби и др.).Системный анализ — это совокупность методов, основанных на использовании ЭВМ и ориентированных на исследование сложных систем. Результат системных исследований - выбор альтернативы: плана развития региона, параметров конструкции и т.д.
К 1979 г. сложилась область исследований, вовлекающая понятия и методы математики, статистики, экономики, управления и психологии – теория принятия решений.
Начиная с 1980 г. и до настоящего времени исследование операций, системный анализ, искусственный интеллект и теория принятия решений – это научные дисциплины «взявшие на себя ответственность» за исследования того, как человек и коллективы людей вырабатывают и принимают решения.
Слайд 7История развития методов и средств исследования операций
Научная сущность исследования операций
История
ИСО неразрывно связана с разработкой математических методов и моделей.
Совокупность
математических методов исследования операций можно разбить на две группы: 1) детерминированные модели: линейное программирование, целочисленное программирование, теория графов, потоки в сетях, геометрическое программирование, нелинейное программирование, теория оптимального управления.
2) стохастические модели: теория массового обслуживания, теория полезности, теория игр, теория поиска, имитационное моделирование и динамическое программирование.
Слайд 8История развития методов и средств исследования операций
Научная сущность исследования операций
В
1939 г. «родилось» линейное программирование. Была напечатана брошюра Леонида Витальевича
Канторовича «Математические методы организации и планирования производства». Однако методы, изложенные Л.В.Канторовичем, были мало пригодны для ручного счета, ЭВМ еще не было и эта работа осталась почти не замеченной.Л.В. Канторович, академик АН СССР, математик, экономист, лауреат Нобелевской премии по экономике в 1975 г.
В 1931 г. венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу, названную «проблема выбора», а метод решения получил название «венгерского метода».
Слайд 9История развития методов и средств исследования операций
Научная сущность исследования операций
Концепции
Л.В. Канторовича после второй мировой войны были переоткрыты на западе.
Американский экономист Т. Купманс привлекал внимание математиков к задачам нахождения экстремумов линейных функций на многогранниках, задаваемых линейными неравенствами и предложил этот раздел математики назвать «Линейное программирование».Американский математик А. Данциг в 1947 году разработал эффективный метод численного решения задач линейного программирования. Он получил название симплекс метода.
Второе рождение линейное программирование получило в начале пятидесятых годов с появлением ЭВМ. В 1975 году академик Л.В.Канторович и профессор Т.Купманс получили Нобелевскую премию по экономическим наукам за «вклад в разработку теории и оптимального использования ресурсов в экономике».
Тьяллинг Чарльз Купманс, доктор наук, профессор, американский экономист и математик, лауреат Нобелевской премии по экономике в 1975 г.
Слайд 10История развития методов и средств исследования операций
Научная сущность исследования операций
С
развитием линейного программирования большое внимание уделялось задачам нелинейного программирования, в которых либо целевая функция,
либо ограничения, либо то и другое нелинейны.В 1951 г была опубликована работа Гарольда Уильяма Куна (американский математик, специалист по теории игр) и Уильяма Альберта Таккера (американский математик), в которой приведены необходимые и достаточные условия оптимальности для решения задач нелинейного программирования.
Слайд 11История развития методов и средств исследования операций
Научная сущность исследования операций
Термин
динамическое программирование впервые был использован в 1940-х годах Ричардом Эрнстом Беллманом (американский
математик, специалист в области вычислительной техники, профессор) для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен рекуррентно только после решения задачи, «предшествующей» ей.Первые задачи теории массового обслуживания были рассмотрены сотрудником Копенгагенской телефонной компании, ученым Аргеном Эрлангом, в период между 1908 и 1922 годами. Стояла задача упорядочить работу телефонной станции и заранее рассчитать качество обслуживания потребителей в зависимости от числа используемых устройств.
Ричард Беллман
Американский математик, один из ведущих специалистов в области математики и вычислительной техники, профессор
Слайд 12История развития методов и средств исследования операций
Научная сущность исследования операций
Метод
Монте-Карло — общее название группы численных методов, основанных на получении большого
числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, математики, экономики, оптимизации, теории управления и др.Станислав Мартин Улам, польско-американский математик, автор метода Монте-Карло, основной разработчик водородной бомбы
Идея метода развита С. Уламом. Он предложил поставить «эксперимент» большое число раз и, таким образом, подсчитав число удачных исходов, оценить их вероятность. Он же предложил использовать компьютеры для расчётов методом Монте-Карло.
Годом рождения метода - 1949 г., когда вышла статья Метрополиса и Улама «Метод Монте-Карло». Название метода происходит от названия города в княжестве Монако, широко известного своими казино с рулеткой - самым известным генератором случайных чисел. В 1950-х годах метод использовался для расчётов при разработке водородной бомбы.
Слайд 13История развития методов и средств исследования операций
Научная сущность исследования операций
Наиболее
важные модели, разработанные с применением методов исследования операций:
Задачи учета,
прогнозирования и планирования производства; Модели финансовой деятельности, управления экономикой, экономического анализа инвестиций, сбыта и рекламы;
Модели управления трудовыми ресурсами;
Модели вычислительных и информационных систем;
Модели выбора, планирования и управления разработкой проекта;
Модели управления запасами;
Модели составления календарных планов производства и последовательности работ;
Модели замены, ремонта и анализа надежности оборудования;
Модели размещения и загрузки производственных мощностей;
Слайд 14История развития методов и средств исследования операций
Научная сущность исследования операций
Применение
методов исследования операций:
военные проблемы,
работа государственных органов,
городские системы,
здравоохранение,
системы образования,
транспорт,
коммунальное обслуживание,
промышленное производство,
технологические процессы.
Слайд 15Предмет и задачи исследования операций
Под исследованием операций понимается применение математических
количественных методов для обоснования решений во всех областях целенаправленной человеческой
деятельности (Е.С. Вентцель, профессор, математик, крупный советский специалист в теории вероятностей, исследовании операций).Исследование операций представляет собой искусство давать плохие ответы на практические вопросы, на которые даются еще худшие ответы другими методами (Т.Л. Саати, США, математик, крупный специалист в исследовании операций и принятии решений)
Исследование операций – 1) применение научного метода, 2) комплексными научными коллективами, 3) для решения задач, связанных с управлением организационными (человеко-машинными) системами с целью получения решений, которые наилучшим образом отвечаю целям всей организации (Р. Акоф, профессор, США, крупный специалист в исследовании операций и управлении, М. Сасиени, Англия, специалистка по управлению и исследованию операций).
Исследование операций – англ. management science, decision science, operations analysis, quantitative analysis, mathematical programming.
Слайд 16Предмет и задачи исследования операций
Предмет исследования операций - системы организационного управления
или организации, которые состоят из большого числа взаимодействующих между собой
подразделений не всегда согласующихся между собой и могут быть противоположны.Цель исследования операций - количественное обоснование принимаемых решений по управлению.
Задачи исследования операций – 1) постановка задачи, 2) построение модели, 3) отыскание решения, 4) проверка модели и оценка решения, 5) внедрение решения и контроль его правильности.
Слайд 17Принципы исследования операций
1. Системный подход к анализу поставленной проблемы.
Системный анализ
является основным методологическим принципом исследования операций, который состоит в том,
что любая задача, какой бы частной она не казалась, рассматривается с точки зрения ее влияния на критерий функционирования всей системы.2. Для исследования операций характерно, что при решении каждой проблемы возникают все новые и новые задачи. Если сначала ставится узкие цели, применение операционных методов неэффективно. Наибольший эффект может быть достигнут только при непрерывном исследовании, обеспечивающем преемственность в переходе от одной задачи к другой.
3. Стремление найти оптимальное решение поставленной задачи. Однако, часто такое решение оказывается недостижимым из-за ограничений, накладываемых имеющимися в наличии ресурсами или уровнем современной науки. Тогда приходится ограничиваться поиском достаточно хорошего или субоптимального решения.
4. Операционные исследования проводятся комплексно, по многим направлениям. Для проведения такого исследования создается операционная группа. В ее состав входят специалисты различных областей: инженеры, математики, экономисты, социологи, психологи.
Слайд 18Ситуация 1
Ситуация 2
Ситуация 3
Лицо, принимающее решения
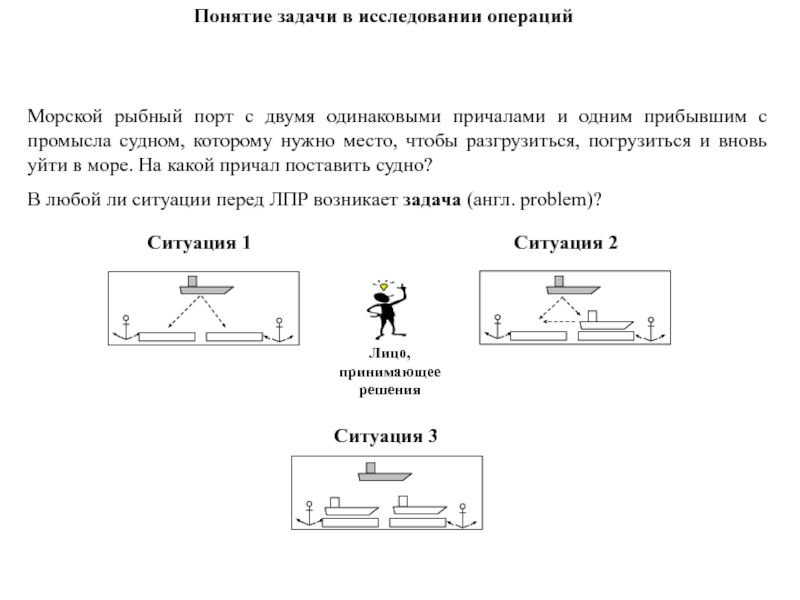
Морской рыбный порт с двумя
одинаковыми причалами и одним прибывшим с промысла судном, которому нужно
место, чтобы разгрузиться, погрузиться и вновь уйти в море. На какой причал поставить судно?В любой ли ситуации перед ЛПР возникает задача (англ. problem)?
Понятие задачи в исследовании операций
Слайд 19Если состояние порта таково, что он простаивает (ситуация 1), т.е.
в распоряжении ЛПР имеются практически неограниченные ресурсы, то первое, что
приходит ему на ум – дать судну любой из двух причалов. При этом ЛПР имело две альтернативы: "поставить судно на левый причал" и "поставить судна на правый причал".В ситуации 2 не так все очевидно, как может показаться на первый взгляд. Число альтернатив не изменилось. Их по–прежнему две : "предоставить судну свободный причал", а также "перешвартовать стоящее у причала судно на другой причал и предоставить освободившееся место пришедшему с промысла". Конечно, в этом случае ЛПР должно отдавать себе отчет в том, чего оно хочет, т.е. какова его цель? Если цель – быстрее начать выгрузку грузов с промысла, то состояние-результат, которого можно достичь при реализации первой альтернативы более предпочтительно, т.е. в этом случае цель будет достигнута вероятнее, чем при реализации второй альтернативы (хотя, если ввести тип судна, расстояние от судна, двигающегося в порт, количество груза на его борту и то, что судно у причала простаивает, то можно склониться и ко второму варианту).
Анализ ситуаций
Слайд 20Впервые ЛПР задумается над ситуацией 3. Число возможных альтернатив увеличилось:
"не прерывать обработку ни одного из двух судов, а поставить
вновь пришедшее вторым бортом к левому судну", "не прерывать обработку ни одного из двух судов, а поставить вновь пришедшее вторым бортом к правому судну", "прервать обработку левого судна, поставить его вторым бортом к правому, поставить вновь прибывшее на освободившийся причал" и т.п.Если учесть целеполагание и оценки достижения цели, то можно сказать, что возникла задача.
Принято считать [Акоф, Сасиени, 1971], что задача существует тогда, когда: 1) существует субъект, перед которым возникает задача; 2) в распоряжении субъекта имеется минимум две альтернативы, т.е. есть выбор; 3) существует цель, которую он стремится достичь; 4) существуют оценки, по которым можно сравнить альтернативы и судить о достижении цели.
Однако для ЛПР существующая задача становится предметом решения только тогда, когда оно не знает , какая альтернатива наилучшая и именно это ему и требуется определить.
Анализ ситуаций
Слайд 21Оптимизационные задачи в науке и технике и принятие решений
Две
задачи исследования операций
1. План снабжения предприятий. Есть предприятия, потребляющих известное
сырье, и сырьевые базы, которые могут поставлять это сырье предприятиям. Базы связаны с предприятиями путями сообщения: ж/д, водными, автомобильными, воздушными со своими тарифами. Требуется разработать такой план снабжения предприятий сырьем (с какой базы, в каком количестве и какое сырье доставляется), чтобы потребности в сырье были обеспечены при минимальных расходах на перевозки.2. Постройка участка магистрали. Сооружается участок ж/д магистрали. В распоряжении ЛПР — определенное количество средств: людей, строительных машин, ремонтных мастерских, грузовых автомобилей и т. д. Требуется спланировать строительство (назначить очередность работ, распределить машины и людей по участкам пути, обеспечить ремонтные работы) так, чтобы оно было завершено в минимально возможный срок.
Слайд 22Цель - желаемое состояние объекта в будущем.
Целеполагание - осмысление своей деятельности ЛПР с
точки зрения формирования (постановки) целей и их реализации (достижения) наиболее
экономичными (рентабельными) средствами.Альтернатива (решение) - определенный выбор параметров зависящих от ЛПР. Решения могут быть удачными и неудачными, разумными и неразумными.
Критерий (гр. kriterion - признак для суждения) — количественный признак, основание, мерило оценки альтернатив (решений).
Оптимальные решения - имеющие, наивысшую – максимальную (max) или наинизшую – минимальную (min) оценку по критерию.
Рациональные решения - решения, по тем или другим признакам (чаще всего качественным, не выраженным количественно) предпочтительные перед другими.
Операция - мероприятие (система действий), объединенное единым замыслом и направленное к достижению цели. Операция всегда управляемое мероприятие, т.е. от ЛПР зависит, каким способом выбрать некоторые параметры, характеризующие ее организацию.
Основные понятия исследования операций
Слайд 23
Элементы решения - параметры, совокупность которых образует решение. В качестве
элементов решения могут фигурировать числа, векторы, функции.
Например, если составляется
план перевозок однородных грузов из пунктов отправления в пункты назначения , то элементами решения будут числа , показывающие, какое количество груза будет отправлено из i-го пункта отправления в j-й пункт назначения . Совокупность чисел и образует решение.В простейших задачах исследования операций количество элементов решения может быть сравнительно невелико. Но в большинстве задач, имеющих практическое значение, число элементов решения очень велико.
Основные понятия исследования операций
Слайд 24Ограничения (дисциплинирующие условия) – пределы в которых ЛПР может распоряжаться
элементами решения. Пределы зафиксированы с самого начала и нарушены быть
не могут (например, грузоподъемность машины; размер планового задания; весовые характеристики оборудования и т. п.). В частности, к таким условиям относятся средства (материальные, технические, людские), которыми ЛПР вправе распоряжаться, и иные ограничения, налагаемые на решение.Область допустимых решений - множество возможных с точки зрения ограничений элементов решения.
Целевая функция – отображение элементов решения на количественные оценки показателя эффективности (критерия), показывающее наилучшее поведение (переход из состояния в состояние) объекта при достижении цели. Выбирая решение, ЛПР,
предпочтет такое, которое обращает показатель эффективности в максимум (или же в минимум).
Целевая функция студента?
Сколько экзаменов сдает студент за четыре года обучения? Ответ: 4 экзамена в сессию, две сессии в год – итого 32 экзамена.
Обозначим - экзаменационную оценку. Тогда целевая функция студента имеет вид:
-
Основные понятия исследования операций
Слайд 251. План снабжения предприятий. Задача операции - обеспечить снабжение сырьем
при минимальных расходах на перевозки. Показатель эффективности R — суммарные
расходы на перевозки сырья за единицу времени, например,месяц:
2. Постройка участка магистрали. Требуется так спланировать строительство, чтобы закончить его как можно скорее. Естественным показателем эффективности было бы время завершения стройки, если бы оно не было связано со случайными факторами (отказы техники, задержки в выполнении отдельных работ).Поэтому в качестве показателя эффективности можно выбрать среднее ожидаемое время Т окончания стройки:
Две задачи исследования операций Целевые функции
Слайд 26Принятие решений
Принятие решений – особый вид целенаправленной деятельности, заключающийся в
выборе одной из имеющихся альтернатив.
Элементы процесса принятия решений:
Задача (проблема), подлежащая
разрешению;Принимающий решение ()решающий) элемент – человек или коллективный орган, который (при помощи технических средств) решает задачу;
Одна или несколько целей в соответствии с которыми осуществляется выбор;
Несколько (множество) альтернатив, среди которых производится выбор.
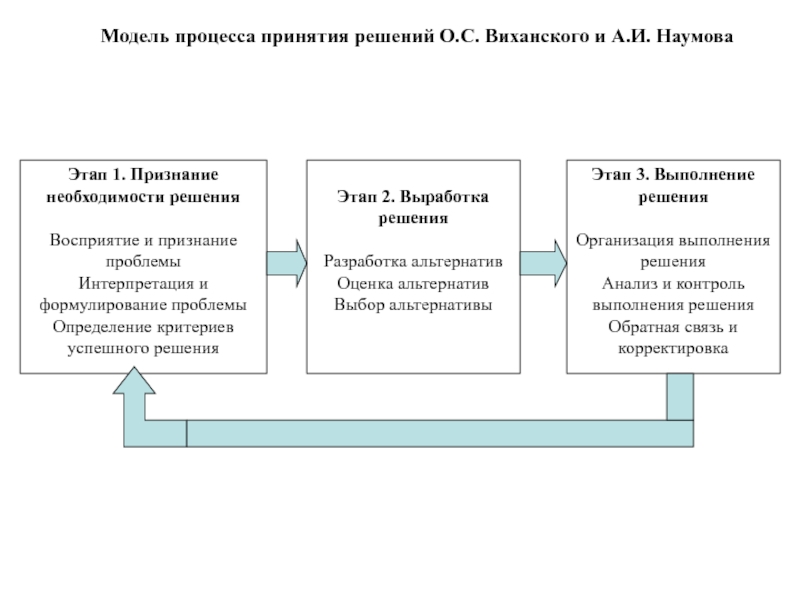
Слайд 27Модель процесса принятия решений О.С. Виханского и А.И. Наумова
Этап 1.
Признание необходимости решения
Восприятие и признание проблемы
Интерпретация и формулирование проблемы
Определение критериев
успешного решения
Этап 2. Выработка решения
Разработка альтернатив
Оценка альтернатив
Выбор альтернативы
Этап 3. Выполнение решения
Организация выполнения решения
Анализ и контроль выполнения решения
Обратная связь и корректировка
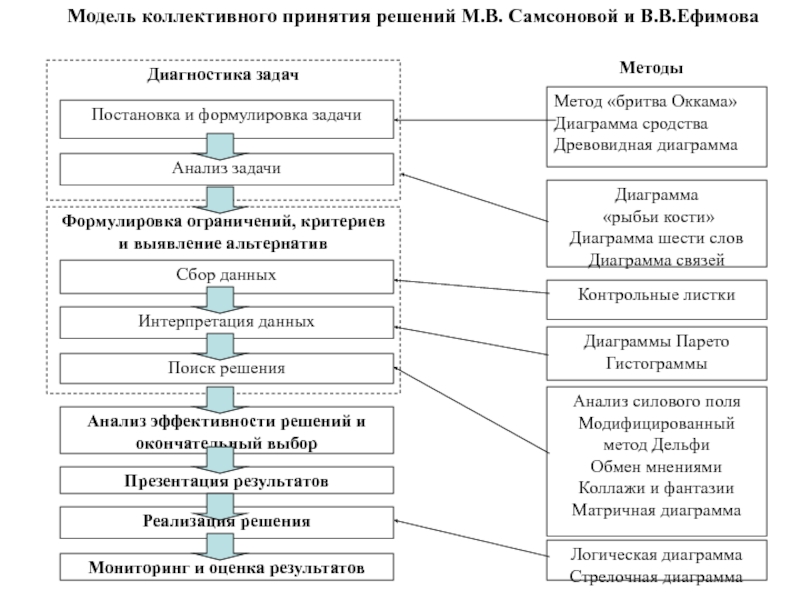
Слайд 28Модель коллективного принятия решений М.В. Самсоновой и В.В.Ефимова
Методы
Диагностика задач
Постановка и формулировка задачи
Анализ задачи
Метод «бритва Оккама» Диаграмма сродства
Древовидная диаграмма
Диаграмма
«рыбьи кости»Диаграмма шести слов
Диаграмма связей
Формулировка ограничений, критериев и выявление альтернатив
Сбор данных
Интерпретация данных
Поиск решения
Контрольные листки
Диаграммы Парето Гистограммы
Анализ силового поля
Модифицированный метод Дельфи
Обмен мнениями
Коллажи и фантазии
Матричная диаграмма
Анализ эффективности решений и окончательный выбор
Презентация результатов
Реализация решения
Мониторинг и оценка результатов
Логическая диаграмма
Стрелочная диаграмма
Слайд 30Автор графика – Михай Чиксентмихайи, профессор психологии Чикагского университета. Люди
часто используют метафору потока, чтобы описать ощущение легкости при выполнении
какого-то дела (например, принимают решения). Основное условие для попадания в это состояние – баланс сложности и навыков в конкретной задаче. Если вызов, который предъявляет вам ситуация, слишком велик – ЛПР начинает нервничать. Если он слишком мал – ЛПР не интересно. Лучшие решения принимаются “в потоке”, когда не скучно, и не страшно.Психология принятия решений
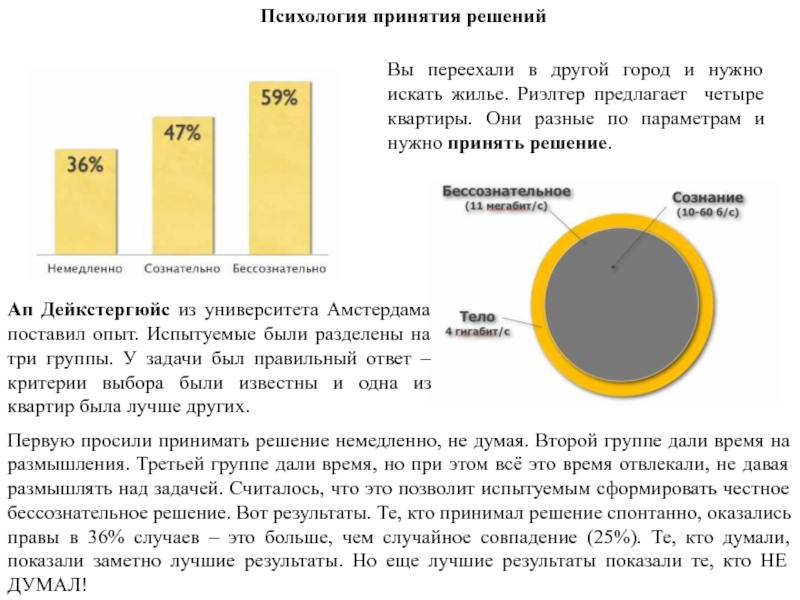
Слайд 31Первую просили принимать решение немедленно, не думая. Второй группе дали
время на размышления. Третьей группе дали время, но при этом
всё это время отвлекали, не давая размышлять над задачей. Считалось, что это позволит испытуемым сформировать честное бессознательное решение. Вот результаты. Те, кто принимал решение спонтанно, оказались правы в 36% случаев – это больше, чем случайное совпадение (25%). Те, кто думали, показали заметно лучшие результаты. Но еще лучшие результаты показали те, кто НЕ ДУМАЛ!Вы переехали в другой город и нужно искать жилье. Риэлтер предлагает четыре квартиры. Они разные по параметрам и нужно принять решение.
Ап Дейкстергюйс из университета Амстердама поставил опыт. Испытуемые были разделены на три группы. У задачи был правильный ответ – критерии выбора были известны и одна из квартир была лучше других.
Психология принятия решений
Слайд 32Закон Йеркса - Додсона (Yerkes-Dodson)- психологический закон, сформулирован 1908 году,
который показывает успешность в зависимости от уровня мотивации на задачах
различной сложности. Он был многократно проверен: на животных и людях. Результаты всегда одни и те же: для каждой задачи существует оптимум мотивации и превышение этого оптимума МЕШАЕТ, а не помогает. Лишняя мотивация мешает. Причем не только отрицательная (наказание), но и положительная!Притча о наказании наградой: “Каждый день одного пожилого человека оскорбляла ватага десятилетних мальчишек, которые проходили мимо его дома по дороге в школу. Однажды он вышел к ним и сказал: “Завтра за каждое ругательство в мой адрес я дам вам доллар!”. Мальчишки пришли назавтра и он выполнил свое обещание. Расплатившись, он сказал: “Приходите завтра еще, я буду давать вам по 25 центов”. Завтра повторилась та же история. На следующий день он пообещал им по центу. “По центу?” – возмутились мальчишки. “Мы не будем заниматься этим за цент!” Больше они никогда не приходили. Лишняя мотивация мешает.
Психология принятия решений
Слайд 33Коллективные решения
Системы поддержки принятия решений
Ситуационные комнаты Ситуационные центры
Слайд 34Формальная модель задачи принятия решений
Задача принятия решений может быть представлена
семеркой:
где t - постановка задачи (например, выбрать одну наилучшую в
некотором смысле альтернативу или упорядочить все множество альтернатив); X - множество допустимых альтернатив (решений, вариантов, действий); R - множество критериев оценки степени достижимости поставленных целей; A – множество шкал измерения по критериям (шкалы наименований, порядковые, интервальные, отношений); F – отображение множества допустимых альтернатив в множество критериальных оценок их последствий (исходов); G – система предпочтений решающего элемента; D – решающее правило, отражающее систему предпочтений.Слайд 35Линейное программирование
Задачи линейного программирования
Постановка задачи линейного программирования
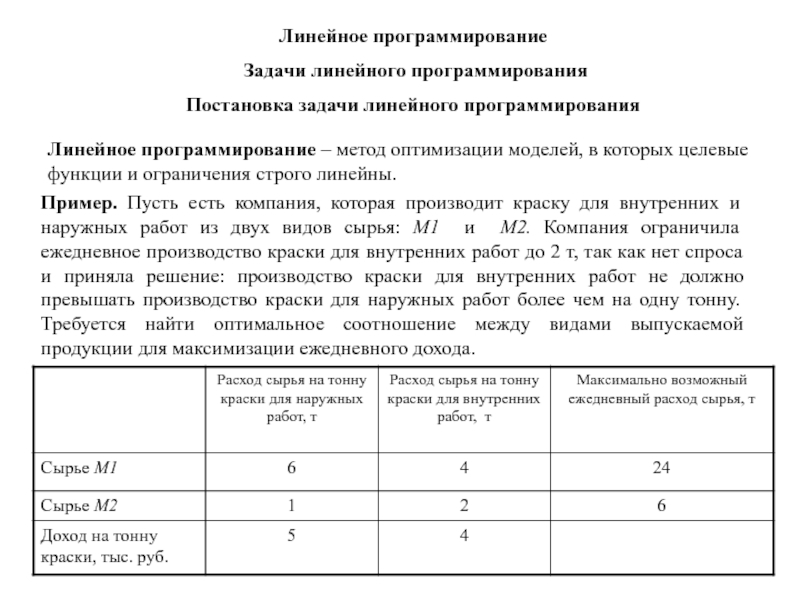
Линейное программирование –
метод оптимизации моделей, в которых целевые функции и ограничения строго
линейны.Пример. Пусть есть компания, которая производит краску для внутренних и наружных работ из двух видов сырья: M1 и M2. Компания ограничила ежедневное производство краски для внутренних работ до 2 т, так как нет спроса и приняла решение: производство краски для внутренних работ не должно превышать производство краски для наружных работ более чем на одну тонну. Требуется найти оптимальное соотношение между видами выпускаемой продукции для максимизации ежедневного дохода.
Слайд 36Линейное программирование
Геометрический смысл задачи линейного программирования
Задача (модель) ЛП, как и
любая задача ИСО, включает три основных элемента.
Переменные, которые следует определить.
Целевая
функция, подлежащая оптимизации.Ограничения, которым должны удовлетворять переменные.
Шаг 1. Определение переменных.
В нашем примере необходимо определить ежедневные объемы производства краски для внутренних и наружных работ. Обозначим эти объемы как переменные модели:
-ежедневный объем производства краски для наружных работ, т;
-ежедневный объем производства краски для внутренних работ, т;
Слайд 37Шаг 2. Построение целевой функции.
Логично предположить, что целевая функция, как
суммарный ежедневный доход, должна возрастать при увеличении ежедневных объемов производства
красок.В соответствии с целями компании получаем задачу:
Линейное программирование
Геометрический смысл задачи линейного программирования
Слайд 38Шаг 3. Определение ограничений.
Ограничения должны учитывать возможности ежедневного потребления сырья
и ограниченность спроса на готовую продукцию. Ограничения можно записать в
виде:Из таблицы имеем:
Линейное программирование
Геометрический смысл задачи линейного программирования
Слайд 39Поскольку ежедневный расход сырья М1 и М2 ограничен соответственно 24
и 6 тоннами, получим следующие ограничения:
Есть еще два ограничения по
спросу на продукцию. Первое: ежедневный объем производства краски для внутренних работ не должен превышать ежедневный объем производства краски для наружных работ: Второе ограничение: максимальный ежедневный обюъем производства краски для внутренних работ не должен превышать 2 т :
Еще одно ограничение: переменные и должны быть неотрицательными (условие неотрицательности переменных):
Линейное программирование
Геометрический смысл задачи линейного программирования
Слайд 40Окончательно задача будет записана следующим образом:
При выполнении ограничений:
Любое решение, удовлетворяющее
ограничениям модели называется допустимым. Например, решение
и будет допустимым, так как не нарушает ни одного ограничения. Значение целевой функции при этом решении будет равно z = 5 х 3 + 4 х 1 = 19 (тыс. руб.)Линейное программирование
Геометрический смысл задачи линейного программирования
Слайд 41Поиск оптимального решения
Как найти оптимальное допустимое решение, доставляющее максимум целевой
функции?
Выводы:
Задача имеем много (бесконечно много) допустимых решений.
Нельзя применять простой перебор,
как метод поиска оптимальных допустимых решений.Необходима эффективная поисковая процедура
Графический способ решения задач линейного программирования
Графический способ состоит из двух этапов:
Построение области допустимых решений, удовлетворяющих всем ограничениям.
Поиск оптимального решения среди всех точек области допустимых решений.
Слайд 43Графический способ решения задач линейного программирования
Случай максимизации целевой функции
Построение области
допустимых решений
Шаг 1. Проведем оси: на оси абсцисс будем указывать
значения , а на оси ординат Шаг 2. Отобразим графически ограничения Эти два ограничения показывают, что область допустимых решений (ОДР) будет лежать в первом квадранте.
Шаг 3. Отобразим графически остальные ограничения. Для этого заменим неравенства равенствами, получим уравнения прямых и построим по этим уравнениям прямые.
Шаг 4. Рассматриваем как графически интерпретируются неравенства. Каждое из них делит плоскость ( ) на две полуплоскости, которые располагаются по обе стороны от прямой. Точки, расположенные по одну сторону от прямой – удовлетворяют неравенству, а по другую сторону – нет.
Шаг 6. Проверка на тестовой точке. Тестовой точкой для проверки того, точки какой полуплоскости удовлетворяют неравенству, а какой нет является точка (0,0). Подстановка координат этой точки в неравенство и проверка удовлетворяет или нет эта точка неравенству однозначно идентифицирует полуплоскость. Графически полуплоскости обозначаются стрелочками, привязанными к окружностям. Если прямая проходит через точку (0,0), то в качестве тестовой можно взять и другую точку.
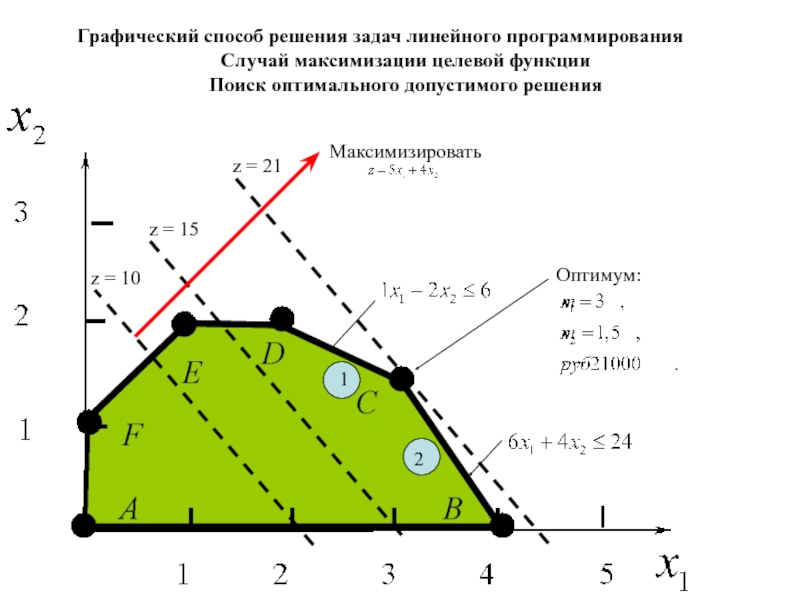
Слайд 44Оптимум:
Максимизировать
z = 10
z = 15
z = 21
1
2
Графический способ решения задач
линейного программирования
Случай максимизации целевой функции
Поиск оптимального допустимого решения
Слайд 45Графический способ решения задач линейного программирования
Случай максимизации целевой функции
Поиск оптимального
допустимого решения
Шаг 1. Определение направления возрастания целевой функции. Для этого
приравняем z к нескольким возрастающим значениям, например, 10 и 15. Подставляем эти значения вместо z ы выражение целевой функции, получаем два уравнения прямых и строим по этим уравнениям графики (пунктир). Проводим стрелку (красный цвет) указывающую направление возрастания значений целевой функции.Шаг 2. Перемещение прямой, соответствующей целевой функции, перпендикулярно направлению возрастания значений целевой функции в сторону стрелки. Перемещение проводится до тех пор, пока график целевой функции будет пересекать ОДР.
Шаг 3. Определение оптимума. Точка пересечения ОДР и прямой, соответствующей максимально возможному значению целевой функции, и будет точкой оптимума.
Слайд 46Графический способ решения задач линейного программирования
Случай максимизации целевой функции
Поиск оптимального
допустимого решения
Оптимальное решение соответствует точке С. Эта точка – место
пересечения прямых (1) и (2), поэтому ее координаты находятся как решение системы уравнений, задающих эти прямые:Решением этой системы будет . При этом значение целевой функции равно
Полученное решение означает, что для компании оптимальным выбором будет ежедневное производство 23 т краски для наружных работ и 1,5 т – для внутренних работ с ежедневным доходом в 21000 руб.
Слайд 47Линейное программирование
Задачи линейного программирования
Нахождение минимума целевой функции
Пример. Компания ежедневно
производит 800 кг добавки – смеси кукурузной и соевой муки.
Состав добавки дан в таблице. Диетологи требуют, чтобы в добавке было не менее 30% белка и не более 5% клетчатки. Компания хочет определить рецептуру смеси минимально стоимости с учетом требований диетологов.Слайд 48Задачи линейного программирования
Нахождение минимума целевой функции
Определяем переменные. Поскольку пищевая добавка
состоит только из кукурузной муки, определим следующие переменные:
- количество кукурузной
муки, используемой в дневном производстве добавки, кг.; - количество соевой муки, используемой в дневном производстве добавки, кг.;
Определяем целевую функцию. Целевая функция равна общей стоимости пищевой добавки, производимой за один день, и должна быть минимальной:
Слайд 49Задачи линейного программирования
Нахождение минимума целевой функции
Введем ограничения. Рассмотрим количество белка
в пищевой добавке. Общее количество белка в смеси, состоящей из
кг. кукурузной муки и соевой муки, равно (кг.) Это количество должно составлять не менее 30% от общего объема смеси . Отсюда получаем следующее неравенство:Аналогично строится ограничение для клетчатки:
Далее нужно переменные из правых частей неравенств перенести в левые части.
Слайд 50Нахождение минимума целевой функции
При выполнении ограничений:
Окончательно модель примет следующий вид:
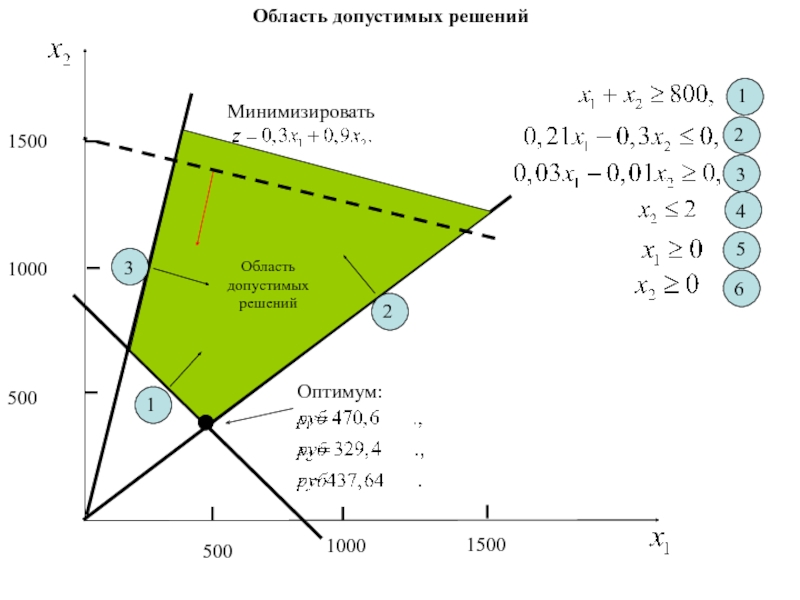
Слайд 52Графический анализ чувствительности
Модель ЛП – «моментальный снимок» реальной ситуации. При
этом параметры модели: коэффициенты целевой функции и неравенств ограничений предполагаются
неизменными.Изучение влияния изменения параметров модели на получение оптимального решения называется анализом чувствительности.
Рассмотрим два случая:
Изменение коэффициентов переменных в целевой функции;
Изменение значений констант в правых частях уравнений ограничений.
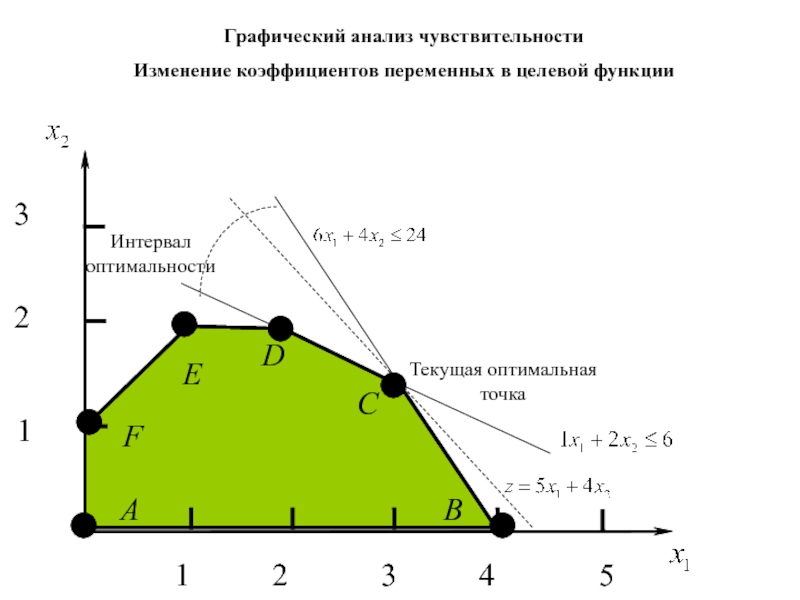
Слайд 54Графический анализ чувствительности
Изменение коэффициентов переменных в целевой функции
Общий вид целевой
функции задачи ЛП с двумя переменными:
Слайд 59Графический анализ чувствительности
Изменение значений констант в правых частях уравнений ограничений
Это
означает, что текущий уровень ресурса М1может быть уменьшен не более
чем на 4 т. и увеличен не более чем на 12 т. В этом случае гарантируется, что оптимальное решение будет достигаться в точке С.Слайд 60Стоимость ресурса i равна:
Изменение значения целевой
функции, соответствующего интервалу осуществимости, деленное на значение интервала осуществимости
Слайд 62Симплекс-метод решения задач линейного программирования
Графический способ решения задач ЛП показал,
что оптимальное решение всегда находится в угловой точке ОДР .
В математике она называется крайней точкой множества.Это явление – ключевая идея алгебраического симплекс-метода для решения задач ЛП. Этот метод ориентирован на компьютерную обработку информации.
Применение СМ требует преобразования зада ЛП к стандартной форме.
Слайд 63Стандартная форма задач линейного программирования
Чтобы перейти к стандартной форме задач
ЛП необходимо выполнить следующие преобразования:
Все ограничения, включая ограничения неотрицательности
переменных преобразовать в равенства с неотрицательной правой частью.Все переменные сделать неотрицательными.
Преобразование неравенств в равенства
Неравенства любого типа (со знаками ) можно преобразовать в равенства добавлением в левую часть дополнительных переменных. Те переменные которые добавляются в неравенства называются остаточными, а в неравенства - избыточными.
Слайд 65Преобразование неравенств в равенства
Преобразование правой части к неотрицательному виду
Эквивалентно равенству:
Умножим
обе части это равенства на -1 , получим равенство с
неотрицательной правой частью:Слайд 66Пример.
Рассмотрим следующую задачу ЛП с двумя переменными:
1
1
2
3
4
2
3
4
5
A
F
E
D
C
B
ОДР
Оптимум:
Стандартная форма задач линейного
программирования
Слайд 67Преобразуем задачу ЛП к стандартной форме:
Стандартная форма задач линейного программирования
Пример
Слайд 68Как определить: какие n - m переменные положить равными нулю,
чтобы получить конкретную угловую точку. Во-первых, это можно сказать только
по графическому представлению ОДР. Во-вторых, это можно только для двух и трех переменных.Однако можно перечислить все угловые точки ОДР. Для этого рассмотрим все комбинации n – m переменных, приравняем их нулю и затем найдем решение полученной системы уравнению. Оптимальное решение будет среди допустимых угловых точек.
Имеем:
угловых точек.
На рисунке видны только четыре точки: А, В,С и D. Есть и точки E и F. Но это недопустимые угловые точки. Они не рассматриваются при поиск оптимума.
Стандартная форма задач линейного программирования
Пример
Комбинаторное число сочетаний из n по m .
Слайд 69Базисные и небазисные переменные
Названия угловых точек на «алгебраическом языке»:
Небазисные (нулевые)
переменные – переменные в количестве n – m , которые
полагаются равными нулю.Базисные переменные – переменные в количестве m , которые доставляют системе уравнений единственное решение
Базисное решение – совокупность базисных переменных.
Допустимое базисное решение – неотрицательное базисное решение.
Слайд 70Размерность задач ЛП
При возрастании размера задачи (при увеличении n и
m) процесс перечисления всех угловых точек становится отдельной сложной задачей.
Например,
при n = 20 и m = 10 необходимо решитьсистем уравнений порядка 10 х 10.
Задачи ЛП размерности 10 х 20 считаются небольшими. Реальные задачи имеют сотни и тысячи переменных. Симплекс-метод частично снимает эту проблему, т.к. рассматривает не все базисные решения (угловые точки ОДР), а только часть допустимых базисных решений.
Слайд 72Алгоритм симплекс-метода
Оба пути A→ B → C и A→
D → C идут вдоль границ ОДР. Причина: симплекс-метод не
может «перескочить» из точки A в точку C сразу.Эмпирическое правило определения факта: какую небазисную переменную сделать положительной в некоторой угловой точке:
«На очередной шаге задачи максимизации выбрать такую небазисную переменную которая имеет наибольший положительный коэффициент в уравнении целевой функции. Если таких переменных несколько, то выбор произвольный».
Применение правила ведет к наименьшему числу итераций алгоритма.
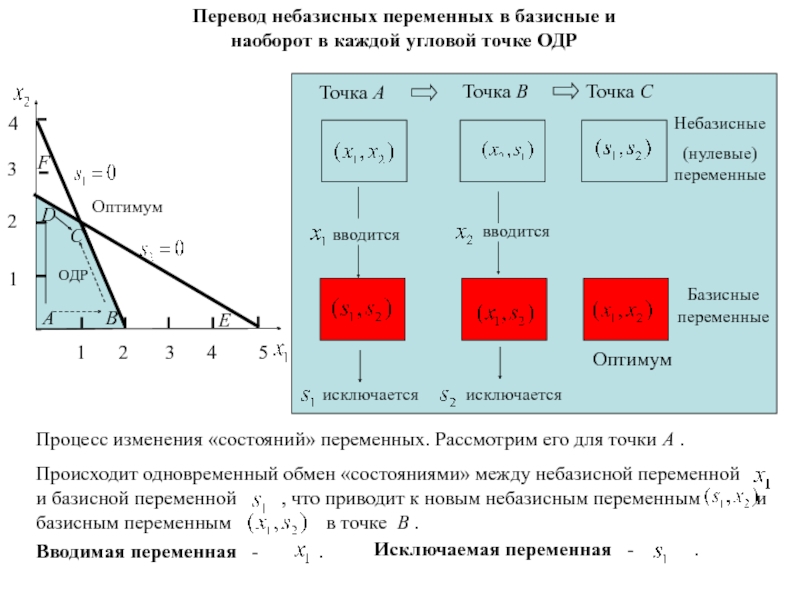
Слайд 73Перевод небазисных переменных в базисные и наоборот в каждой угловой
точке ОДР
Исключаемая переменная -
.Слайд 74При выполнении ограничений:
Алгоритм симплекс-метода
Рассмотрим алгоритм симплекс-метода на примере производства красок.
Запишем
задачу ЛП в стандартной форме:
Представим целевую функцию в виде:
Слайд 78Вычисление нового базисного решения методом Гаусса-Жордано
(Карл Фридрих Гаусс - Вильгельм
Йордан)
Ведущий столбец
Ведущая строка
Ведущий столбец ассоциируется с вводимой переменной.
Ведущая строка ассоциируется
в исключаемой переменной.Элемент на пересечении ведущего столбца и ведущей строки называется ведущим.
Текущая z- строка
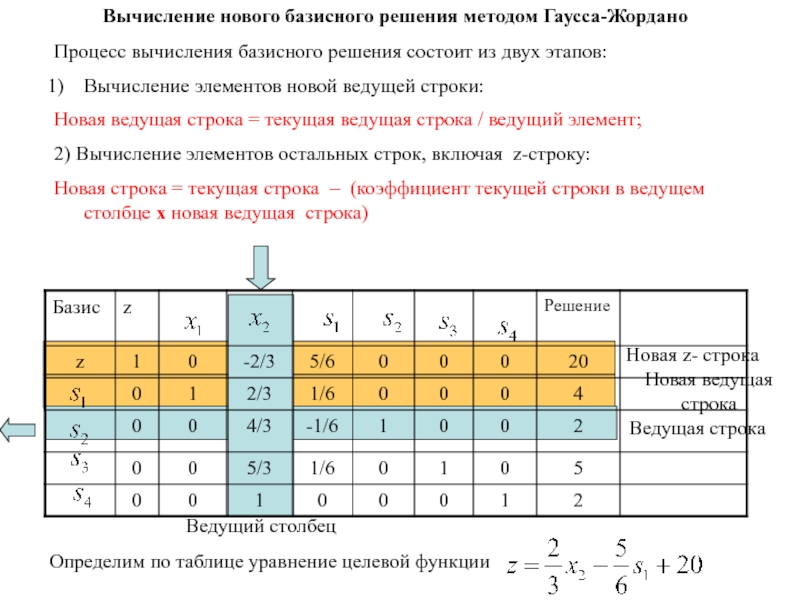
Слайд 79Вычисление нового базисного решения методом Гаусса-Жордано
Процесс вычисления базисного решения состоит
из двух этапов:
Вычисление элементов новой ведущей строки:
Новая ведущая строка
= текущая ведущая строка / ведущий элемент;2) Вычисление элементов остальных строк, включая z-строку:
Новая строка = текущая строка – (коэффициент текущей строки в ведущем столбце х новая ведущая строка)
Определим по таблице уравнение целевой функции
Ведущий столбец
Ведущая строка
Новая ведущая строка
Новая z- строка
Слайд 80Ведущий столбец
Ведущая строка
Ведущий столбец
Ведущая строка
Текущая z- строка
Новая ведущая строка
Новая z-
строка
Слайд 81Процесс вычисления базисного решения состоит из двух этапов:
Вычисление элементов новой
ведущей строки:
Новая ведущая - строка =
текущая ведущая -строка / 6;2) Вычисление элементов остальных строк, включая z-строку:
Новая z-строка = текущая z-строка – (- 5 х новая ведущая строка);
Новая -строка = текущая z-строка – (1 х новая ведущая строка);
Новая -строка = текущая z-строка – (- 1 х новая ведущая строка);
Новая -строка = текущая z-строка – (0 х новая ведущая строка);
Расчеты для одного шага вычислений нового базисного решения методом Гаусса-Жордано
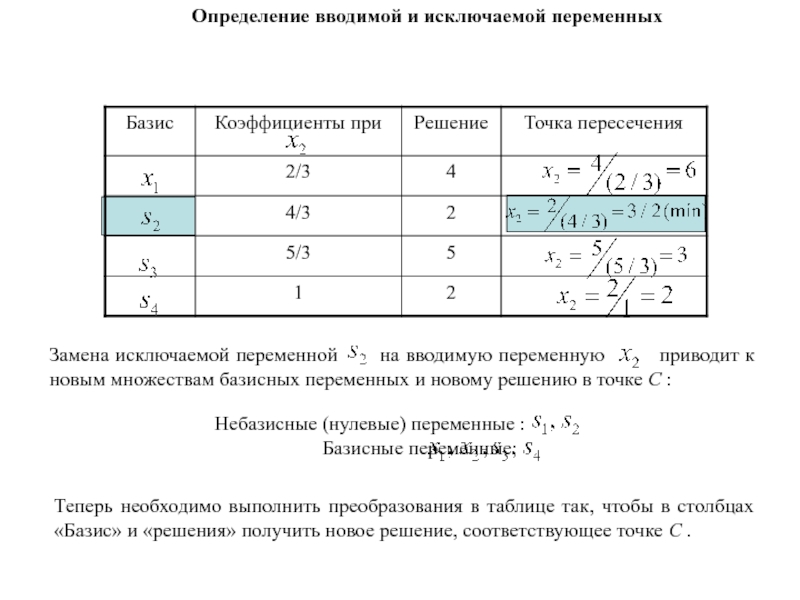
Слайд 82Теперь необходимо выполнить преобразования в таблице так, чтобы в столбцах
«Базис» и «решения» получить новое решение, соответствующее точке С .
Определение
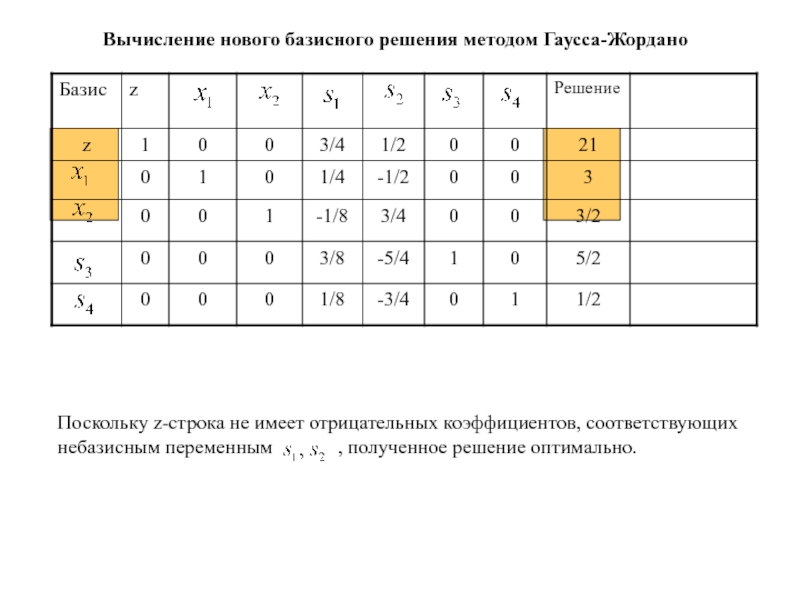
вводимой и исключаемой переменныхСлайд 83Вычисление нового базисного решения методом Гаусса-Жордано
Поскольку z-строка не имеет отрицательных
коэффициентов, соответствующих небазисным переменным
, полученное решение оптимально.Слайд 84Явления вычислительного процесса симплекс-метода
Вырожденность. Проверка условия допустимости может привести к
многозначности в выборе исключаемой переменной. В этом случае на следующей
итерации одна или несколько базисных переменных примут нулевое значение. Тогда новое решение будет вырожденным.С практической точки зрения вырожденность объясняется тем, что в постановке задачи ЛАП есть как min одно избыточное ограничение.
Слайд 85Явления вычислительного процесса симплекс-метода Вырожденность
Информация, что некоторые ресурсы недефицитны, может
быть полезна при интерпретации результатов решения задачи. Эти сведения также
могут помочь выявить неточности и ошибки в постановке задачи. Нет способов определить избыточное ограничение по симплекс-таблицам.С вычислительной точки зрения вырожденность может привести к зацикливанию. С теоретической точки зрения вероятность зацикливания в задачах ЛП, решаемых симплекс-методом очень мала.
Слайд 86Явления вычислительного процесса симплекс-метода Альтернативные оптимальные решения
Альтернативные оптимальные решения. Это
явление возникает когда (для двухмерного случая) прямая, представляющая целевую функцию,
параллельна прямой, соответствующей связывающему неравенству (которое в точке пересечения выполняется как точное равенство). Тогда целевая функция примет одно и то же оптимальное решение на некотором множестве точек границы ОДР. Эти решения называются альтернативными оптимальными решениями.Симплекс-метод может определить только две угловые точки. На практике альтернативные оптимальные решения предоставляют возможность сделать выбор.
Математически можно найти все точки отрезка ВС как взвешенное среднее.
Слайд 87Явления вычислительного процесса симплекс-метода Неограниченная целевая функция
Неограниченная целевая функция. Это
явление возникает, когда в задаче ЛП имеет место не ограниченная
ОДР.В некоторых задачах ЛП значения переменных могут неограниченно возрастать без нарушения ограничений. В результате – целевая функция может возрастать ( при максимизации) или убывать (при минимизации) неограниченно. Неограниченность решения показывает одно – модель разработана не корректно.
Слайд 88Явления вычислительного процесса симплекс-метода Отсутствие допустимых решений
Отсутствие допустимых решений. Явление
возникает, если ограничения задачи ЛП несовместимы, т.е. не могут выполняться
одновременно. Такая ситуация не возникнет, если все неравенства-ограничения имеют тип . На практике возникновение такого явления означает, что задача плохо сформулирована.Псевдооптимальное решение
Слайд 89Двойственность задач линейного программирования
Исходную задачу ЛП будем называть прямой. Двойственная
задача - это задача, формулируемая с помощью определенных правил непосредственно
из прямой.Задача ЛП в стандартной форме записывается так:
Максимизировать или минимизировать целевую функцию
При ограничениях:
В состав n переменных входят и дополнительные переменные.
Стандартная форма задач ЛП приводит к стандартной таблице симплекс-метода.
Слайд 90Правила преобразования прямой в двойственную задачу
Переменные и ограничения двойственной задачи
формируются путем симметричных структурных преобразований прямой задачи по следующим правилам.
Каждому
из m ограничений прямой задачи соответствует переменная двойственной задачи.Каждой из n переменных прямой задачи соответствует ограничение двойственной задачи.
Коэффициенты при какой-либо переменной в ограничениях прямой задачи становятся коэффициентами ограничения двойственной задачи, соответствующего этой переменной. Правая часть формируемого ограничения равна коэффициенту при этой переменной в выражении целевой функции.
Коэффициенты целевой функции двойственной задачи равны правым частям ограничений прямой задачи.
Слайд 91j – ое ограничения
2-задачи
Коэффициенты целевой функции 2-задачи
Преобразование прямой в
двойственную задачу
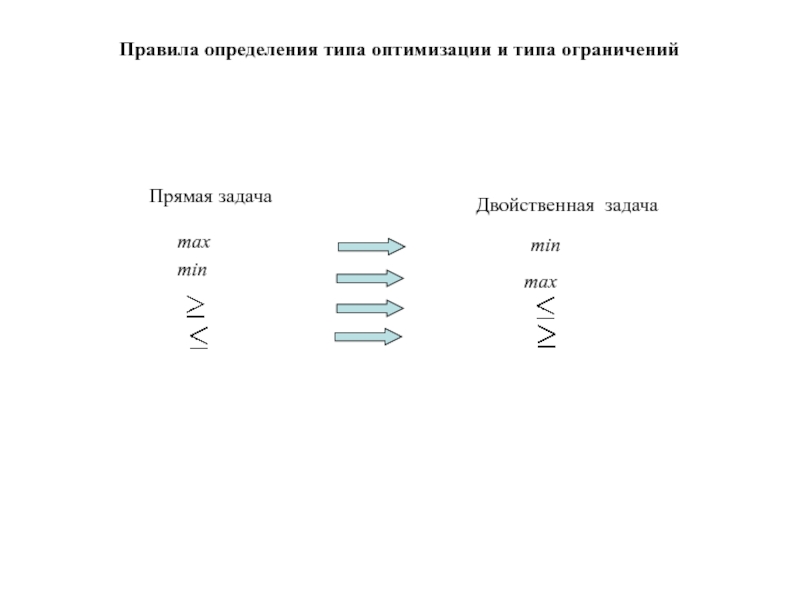
Слайд 92Правила определения типа оптимизации и типа ограничений
Прямая задача
Двойственная задача
max
min
min
max
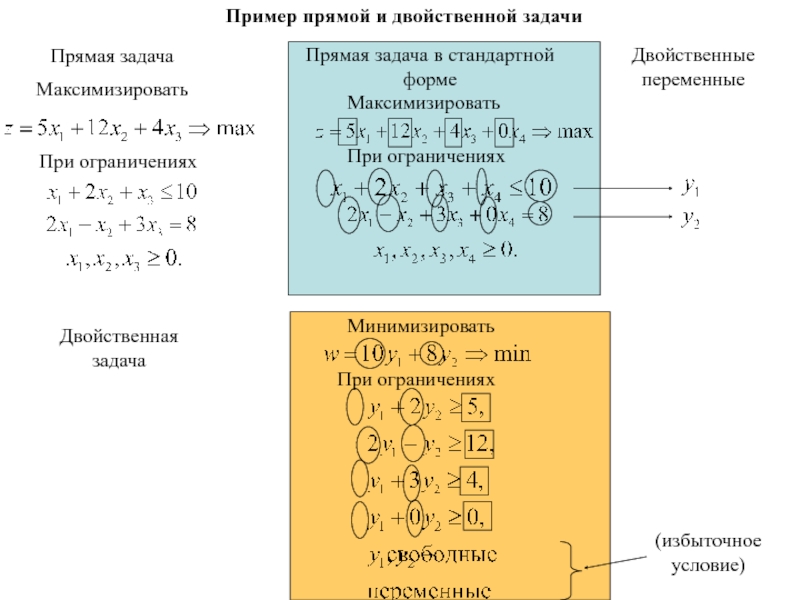
Слайд 93Прямая задача
Максимизировать
При ограничениях
Прямая задача в стандартной форме
Максимизировать
При ограничениях
Двойственные переменные
Двойственная задача
При
ограничениях
Минимизировать
Пример прямой и двойственной задачи
(избыточное условие)
Слайд 94Соотношения между прямой и двойственной задачами ЛП
Двойственной к двойственной задаче
ЛП будет прямая задача.
Поэтому симплекс-метод симметричен относительно прямой и двойственной
задач. Его можно использовать для определения оптимального решения одной задачи непосредственно из симплекс-таблицы, содержащей оптимальное решение другой. Отсюда вычисления можно проводить для той задачи (прямой или двойственной), которая требует меньших вычислительных ресурсов: меньший объем вычислений имеет задача с меньшим количеством ограничений.
Слайд 95Экономическая интерпретация двойственности
Для любой пары допустимых решений прямой и двойственной
задачи значения (конечные) их целевых функций удовлетворяют неравенству
Иными словами –
для всех допустимых решений прямой и 2-задач значения целевой функции задачи минимизации всегда будут верхним пределом значений целевой функции задачи максимизации.Слайд 98Методы решения задач нелинейного программирования
Геометрический метод
Метод множителей Лагранжа
Метод штрафных функций
Генетические
алгоритмы
Слайд 104Рассмотрим задачу: f (X) max , при условии g
(X) = 0.
По склону горы идет дорога, требуется найти на
ней самую высокую точку. На рисунке представлена карта местности с нанесенными на нее линиями равных высот.Толстая линия – это дорога. Точка М, в которой дорога касается одной линий уровня, - это и есть наивысшая точка дороги. Если – точка плотности, и – её координаты, то задаче можно придать следующую форму. Пусть f (Х) — высота точки Х над уровнем моря, а уравнение g ( X) = 0 описывает дорогу. Тогда наивысшая точка дороги - решение задачи.
Если бы дорога проходила через вершину горы, то ее высшая точка была бы самой высокой точкой местности, и ограничение можно было бы не принимать во внимание.
Если же дорога не проходит через вершину, то, немного отклонившись от дороги, можно было бы подняться выше, чем двигаясь строго по дороге. Отклонение от дороги соответствует попаданию в такие точки, где g (X) 0; при малых отклонениях достижимую при этом высоту можно приближенно считать пропорциональной отклонению.
Метод множителей Лагранжа
Простой пример
Слайд 105Идею решения задачи Лагранжа можно представить следующим образом: можно попытаться
“исправить” рельеф местности так, чтобы отклонение от дороги не давало
преимуществ в достижении высоты. Для этого нужно заменить высоту f (Х) функцией.L (X) = f (X) - g (Х),
где множитель подбирается таким образом, чтобы участок склона в окрестности точки М стал горизонтальным (слишком малое не устранит преимуществ отклонений от дороги, а слишком большое – придаст преимущество отклонениям в противоположную сторону).
Теперь, поскольку рельеф L (X) делает площадку в окрестности точки оптимума горизонтальной, эта точка удовлетворяет равенствам
а так как точка лежит на дороге, то – и ограничению g ( X) = 0.
Метод множителей Лагранжа
Простой пример
Разрез горы по АВ
Слайд 107Решив систему уравнений, получим все точки
, в которых функция может имеет экстремумы. Дальше эти точки должны быть дополнительно исследованы.
Слайд 114Используя штрафную функцию, последовательно переходят от одной точки к другой
до тех пор, пока не получат приемлемое решение.
Координаты последующей точки
находят по формуле:Из формулы следует, что если предыдущая точка находится в ОДР, то второе слагаемое в квадратных скобках равно нулю и переход к последующей точке определяется только градиентом целевой функции. Если же указанная точка не принадлежит ОДР, то за счет данного слагаемого на последующих итерациях достигается возвращение в ОДР.
При этом, чем меньше , тем быстрее находится приемлемое решение. Однако точность его определения снижается. Поэтому итерационный процесс начинают при малых значениях и, продолжая его, эти значения постепенно увеличивают.
где - шаг вычислений , вычисляется или выбирается так, чтобы
значение функции , зависящее от ,в точке было максимальным.
Метод штрафных функций
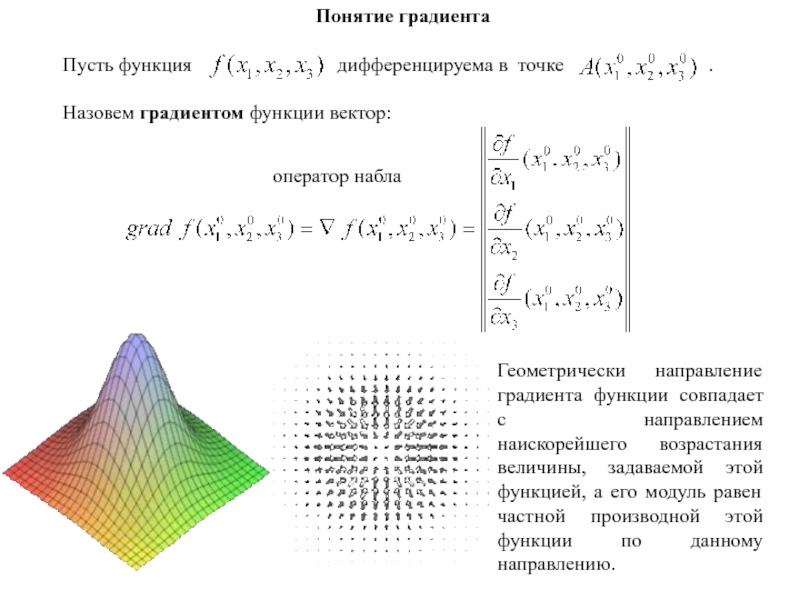
Слайд 115Геометрически направление градиента функции совпадает с направлением наискорейшего возрастания величины,
задаваемой этой функцией, а его модуль равен частной производной этой
функции по данному направлению.Понятие градиента
оператор набла
Слайд 116Найдем градиент функции
в точке A (2, 1 ,1).
1. Находим частные производные функции F :
2. Вычисляем частные производные в точке A (2, 1 ,1):
3. Вычисляем градиент функции F в точке А (2, 1, 1) :
Понятие градиента
Слайд 117Последовательность выполнения этапов метода штрафных функций:
Определяют исходное допустимое решение.
Выбирают шаг
вычислений.
Находят по всем переменным частные производные от целевой функции и
функций, определяющих ОДР.Находят по формуле для координаты точки, определяющей возможное новое решение задачи.
Проверяют, удовлетворяют ли координаты найденной точки системе ограничений задачи. Если нет, то переходят к следующему этапу. Если координаты найденной точки определяют допустимое решение задачи, то исследуют необходимость перехода к последующему решению. В случае такой необходимости переходят к этапу 2, в противном случае найдено приемлемое решение исходной задачи.
Устанавливают значения весовых коэффициентов и переходят к этапу 4.
Метод штрафных функций
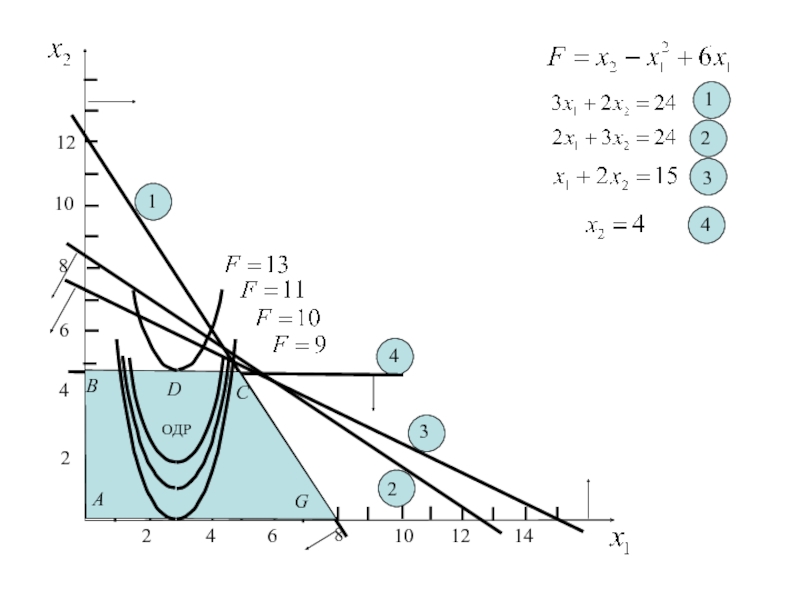
Слайд 118Пример
Найти максимальное значение функции:
При условиях:
Построим ОДР задачи и линии
уровня для целевой функции. Этими линиями служат окружности в центром
в точке (0; 0). Точка касания одной из этих окружностей с ОДР и является искомой точкой максимального значения целевой функции.Метод штрафных функций
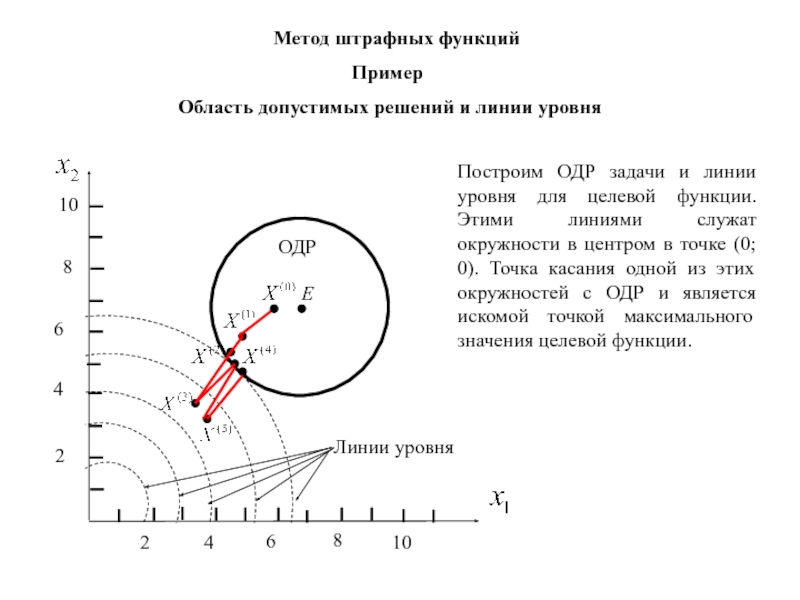
Слайд 119Метод штрафных функций
Пример
Область допустимых решений и линии уровня
Построим ОДР
задачи и линии уровня для целевой функции. Этими линиями служат
окружности в центром в точке (0; 0). Точка касания одной из этих окружностей с ОДР и является искомой точкой максимального значения целевой функции.Слайд 126Сравнивая значения целевой функции, найденные в точках после 10 и
12 итераций, видим, что они с точностью до 0,1 совпадают.
Это говорит о близости точки, найденной на последней итерации, к точке максимального значения целевой функции.Пример
Метод штрафных функций
Слайд 127Динамическое программирование
Словосочетание динамическое программирование впервые было использовано в 1940 -х годах
Ричардом Беллманом для описания процесса нахождения решения задачи, где ответ
на одну задачу может быть получен только после решения задачи, «предшествующей» ей.Слово «программирование» в словосочетании «динамическое программирование» происходит от словосочетания математиче6ское программирование - синонима слова «оптимизация». Слово «программа» в данном контексте означает оптимальную последовательность действий для получения решения задачи.
Ричард Беллман
Американский математик, один из ведущих специалистов в области математики и вычислительной техники, профессор
Слайд 128Динамическое программирование
Динамическое программирование (ДП) определяет оптимальное решение n – мерной
задачи путем ее декомпозиции на n этапов, каждый из которых
есть подзадача относительно одной переменной.Вычислительное преимущество ДП – решаются одномерные оптимизационные задачи вместо большой n-мерной задачи. ДП не использует «собственных» вычислительных алгоритмов непосредственно для каждого этапа. Эти алгоритмы проектируются и реализуются по отдельности. Например, это могут быть алгоритмы ЛП.
Рекуррентная природа вычислений в динамическом программировании
Вычисления в ДП рекуррентные в том смысле, что оптимальное решение одной подзадачи – исходные данные для следующей. Решение последней задачи – оптимальное решение исходной задачи.
Слайд 129Динамическое программирование
Понятия декомпозиции и редукции
Декомпозиция — научный метод, использующий структуру задачи
и позволяющий заменить решение одной большой задачи решением серии меньших
задач.Расчлените каждую изучаемую Вами задачу на несколько частей, на сколько сможете и на сколько это потребуется Вам, чтобы их было легко решить.
Р. Декарт.
Редукция (лат. reductio — возвращение, приведение обратно) восстановление прежнего состояния, сведение сложного к более простому. Редуцирование —наименование процессов, ведущих к уменьшению размеров какого-либо объекта, упрощению его структуры или к ослаблению напряжения, силы, иногда к полному исчезновению чего-либо.
Редукция - методологический приём, играющий, важнейшую роль в логике, математике и др. дедуктивных науках. Редукция состоит в преобразовании данных (задач, предложений и т. п.) в наиболее удобный с какой-либо точки зрения вид, например в выражении их в форме логически более простой и легче поддающейся анализу.
Слайд 130Динамическое программирование
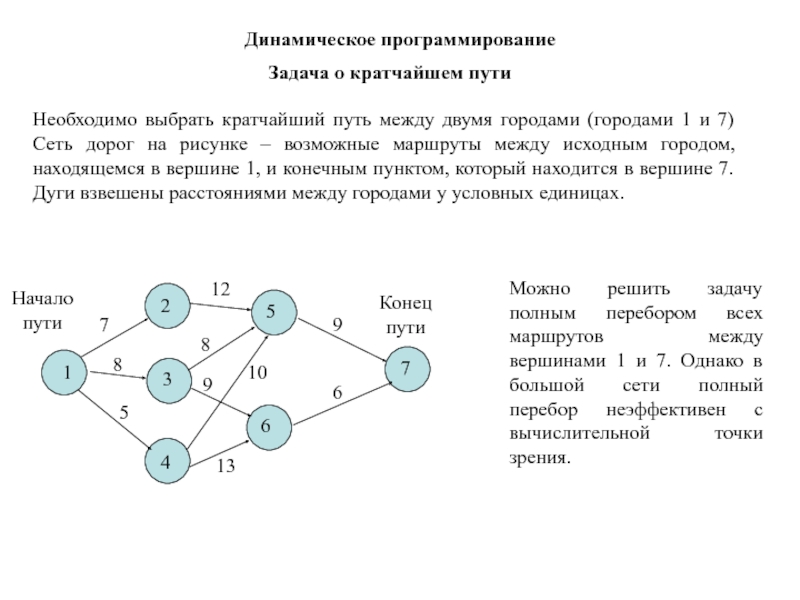
Задача о кратчайшем пути
Необходимо выбрать кратчайший путь между двумя
городами (городами 1 и 7) Сеть дорог на рисунке –
возможные маршруты между исходным городом, находящемся в вершине 1, и конечным пунктом, который находится в вершине 7. Дуги взвешены расстояниями между городами у условных единицах.1
2
3
4
5
6
7
7
8
5
12
8
9
10
13
9
6
Начало пути
Конец пути
Можно решить задачу полным перебором всех маршрутов между вершинами 1 и 7. Однако в большой сети полный перебор неэффективен с вычислительной точки зрения.
Слайд 131Динамическое программирование
Задача о кратчайшем пути
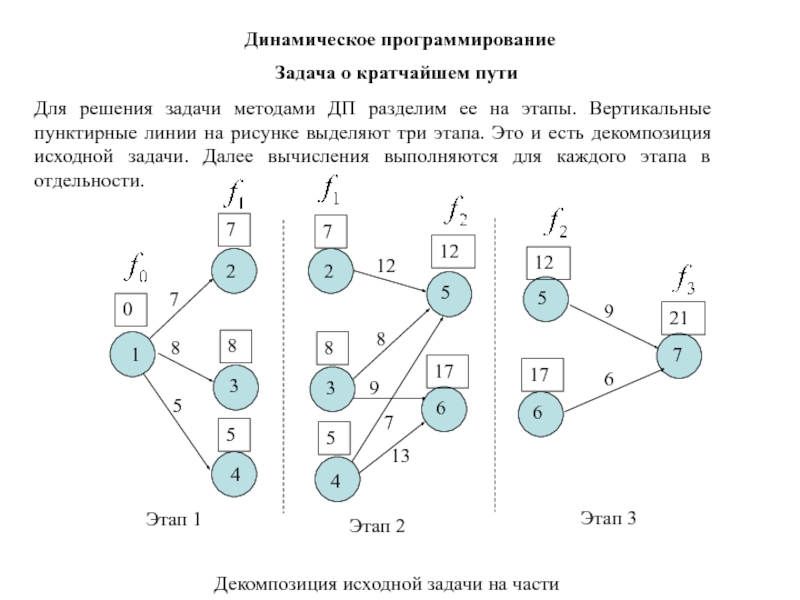
Для решения задачи методами ДП разделим
ее на этапы. Вертикальные пунктирные линии на рисунке выделяют три
этапа. Это и есть декомпозиция исходной задачи. Далее вычисления выполняются для каждого этапа в отдельности.Декомпозиция исходной задачи на части
Слайд 132Динамическое программирование
Задача о кратчайшем пути
Общая задача состоит в вычислении кратчайших,
постепенно накапливаемых расстояний ко всем вершинам этапа с последующим использованием
этих расстояний в качестве исходных данных для следующего этапа.Для первого этапа имеем следующие вычисления:
Этап 1. Итоговые результаты:
Кратчайший путь из вершины 1 в вершину 2 – 7 км; 1 →3 – 8 км; 1 → 4 – 5 км.
Переходим к этапу 2 вычисления кратчайших (накопленных) расстояний к вершинам 5 и 6. Рассматриваем вершину 5 первой. Есть 3 маршрута для достижения вершины 5: (2,5), (3,5) и (4,5). Эта информация вместе с кратчайшими расстояниями к узлам 2, 3 и 4 определяет кратчайшее (накопленное) расстояние к вершине 5 следующим образом:
Слайд 133Динамическое программирование
Задача о кратчайшем пути
Этап 2. Итоговые результаты:
Кратчайший путь из
вершины 4 в вершину 5 – 12 км;
3 →6 – 17 км;Последний шаг – третий этап. Конечную вершину 7 можно достичь из вершин 5 и 6. Используя итоговые результаты этапа 2 и расстояния от вершин 5 и6 к вершине 7, получим
Этап 3. Итоговые результаты:
Кратчайший путь к вершине 7 равен 21 км (из вершины 5);
Кратчайшее расстояние между вершинами 1 и 7 равно 21 км.
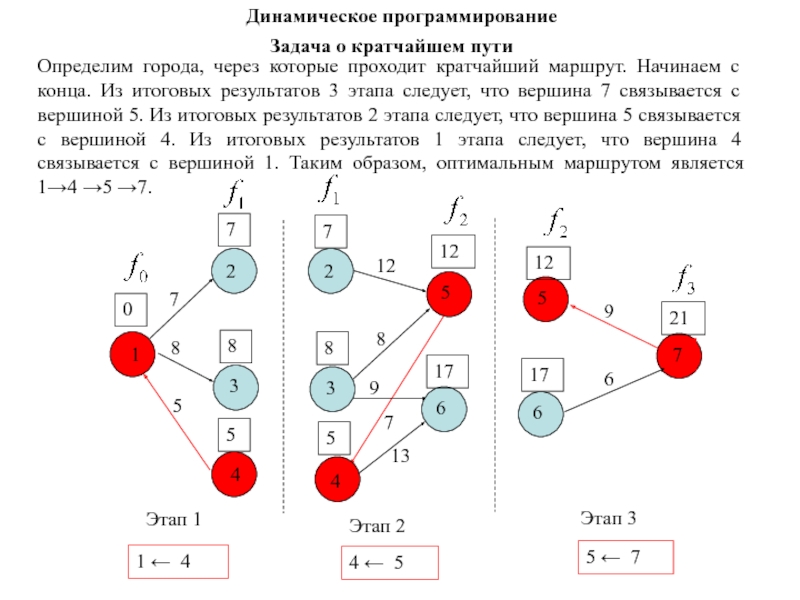
Слайд 134Определим города, через которые проходит кратчайший маршрут. Начинаем с конца.
Из итоговых результатов 3 этапа следует, что вершина 7 связывается
с вершиной 5. Из итоговых результатов 2 этапа следует, что вершина 5 связывается с вершиной 4. Из итоговых результатов 1 этапа следует, что вершина 4 связывается с вершиной 1. Таким образом, оптимальным маршрутом является 1→4 →5 →7.1
2
3
4
5
6
7
8
5
12
8
9
7
13
2
3
4
5
6
7
9
6
0
7
8
5
7
8
5
12
17
12
17
21
Этап 1
Этап 2
Этап 3
1 ← 4
4 ← 5
5 ← 7
Динамическое программирование
Задача о кратчайшем пути
Слайд 136Динамическое программирование
В действительности состояние системы на этапе i - это
информация, связывающая этапы между собой. При этом оптимальные решения для
оставшихся этапов могут приниматься без повторной проверки того, как были получены решения на предыдущих этапах.Такое определение состояния системы позволяет рассматривать каждый этап отдельно и гарантирует, что решение является допустимым на каждом этапе. Определение состояния системы приводит к следующему унифицированному положению.
Принцип оптимальности. На каждом этапе оптимальная стратегия определяется независимо от стратегий, использованных на предыдущих этапах.
Слайд 137Рассмотренный выше пример, когда вычисления выполнялись последовательно, от первого этапа
до третьего раскрывает суть алгоритма прямой прогонки. Известен и алгоритм
обратной прогонки, вычисления в соответствии с которым выполняются от третьего этапа до первого.Оба алгоритма приводят к одному и тому же результату. Покажем использование алгоритма обратной прогонки, применив табличную форму.
где для . Последовательность вычислений .
Алгоритм обратной прогонки
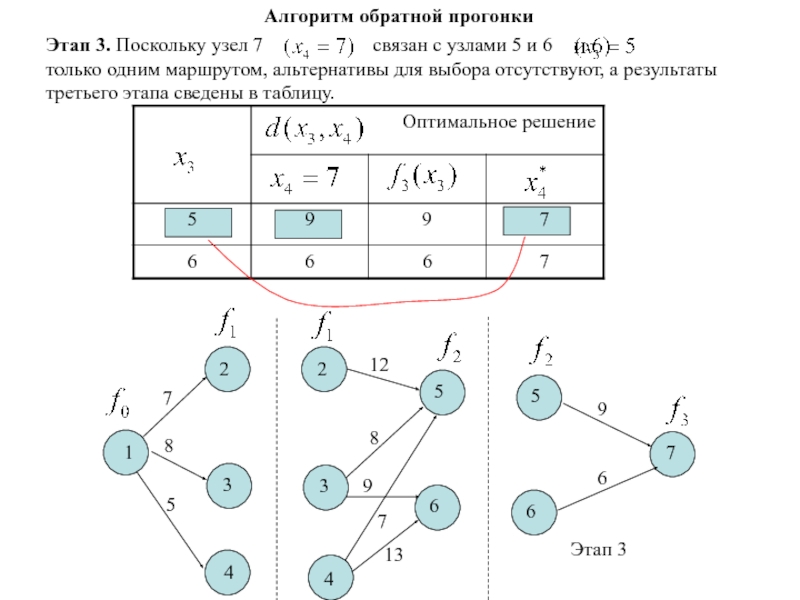
Слайд 138Этап 3. Поскольку узел 7
связан с узлами 5 и
6 только одним маршрутом, альтернативы для выбора отсутствуют, а результаты третьего этапа сведены в таблицу.1
2
3
4
5
6
7
8
5
12
8
9
7
13
2
3
4
5
6
7
9
6
Этап 3
Алгоритм обратной прогонки
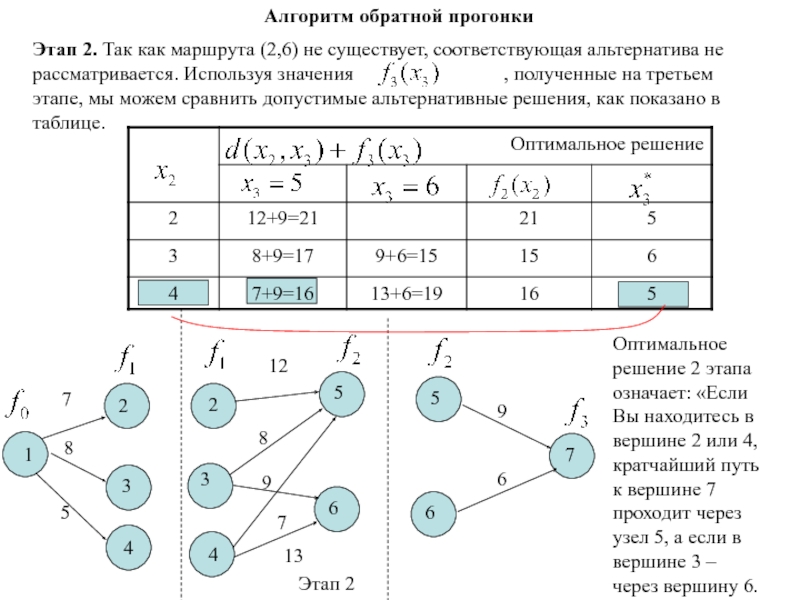
Слайд 139Этап 2. Так как маршрута (2,6) не существует, соответствующая альтернатива
не рассматривается. Используя значения
, полученные на третьем этапе, мы можем сравнить допустимые альтернативные решения, как показано в таблице.1
2
3
4
5
6
7
8
5
12
8
9
7
13
2
3
4
5
6
7
9
6
Этап 2
Оптимальное решение 2 этапа означает: «Если Вы находитесь в вершине 2 или 4, кратчайший путь к вершине 7 проходит через узел 5, а если в вершине 3 – через вершину 6.
Алгоритм обратной прогонки
Слайд 140Этап 1. Из вершины 1 начинаются три альтернативных маршрута: (1,2),
(1,3) и (1,4). Используя значения
, полученные на втором этапе, вычисляем данные следующей таблицы.Оптимальное решение на первом этапе показывает, что кратчайший путь проходит через вершину1. Далее из оптимального решения на этапе 2 следует, что из города 4 нужно двигаться в город 5. Из оптимального решения на этапе 3 следует, что вершина 5 связана с вершиной 7. Следовательно, полным маршрутом с кратчайшей длиной, является 1→4 →5 →7 и его длина – 21 км.
Алгоритм обратной прогонки
Слайд 141Безусловная оптимизация
Поиск экстремумов функций в условиях отсутствия ограничений на значения
переменных называется безусловной оптимизацией. Иными словами подобные задачи называют экстремальными
задачами без ограничений.Основные понятия экстремальных задач без ограничений
Экстремальная точка функции определяет либо ее максимальное, либо минимальное значение. С математической точки зрения точка
является точкой максимума функции , если неравенство
выполняется для всех , таких, что
достаточно малы при всех других j . Другими словами, точка является точкой максимума, если значения функции в окрестности точки не превышают
. Аналогично точка является точкой минимума функции , если для определенного выше вектора h имеет место неравенство
Слайд 143Методы оптимизации
Методы одномерной оптимизации
Методы безусловной оптимизации
Методы условной оптимизации
Методы моделирования эволюции
Методы
оптимизации
Методы имитирующие интеллект роя
Слайд 144Методы одномерной оптимизации
Метод дихотомического поиска
Метод золотого сечения
Метод чисел Фибоначчи
Метод
полиномиальной аппроксимации
Слайд 145Методы безусловной оптимизации
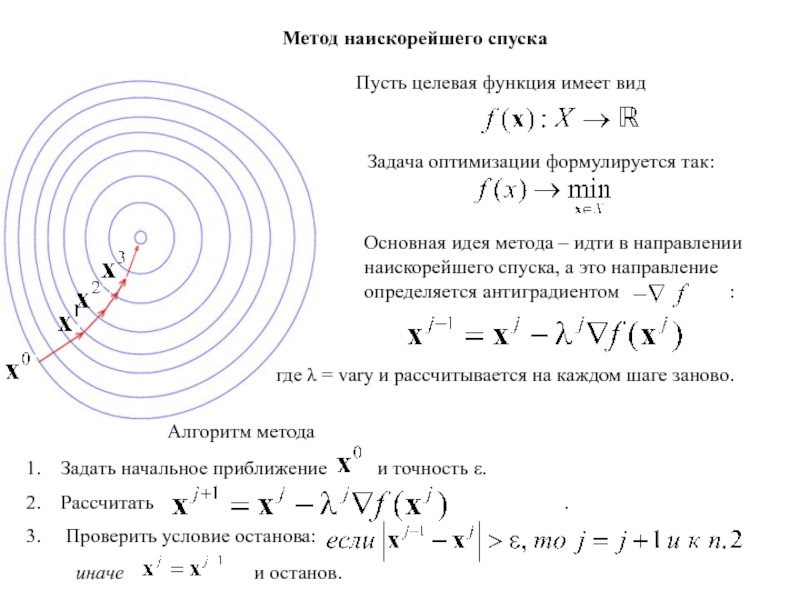
Метод наискорейшего спуска
Метод Розенблока
Метод конфигураций
Метод Хука-Дживса
Метод деформируемого многогранника
Метод
Нелдера-Мида
Метод случайного поиска
Метод сопряженных градиентов
Метод Флетчера-Ривса
Метод Ньютона
Метод переменной метрики
Метод Девидсона-Флетчера-Пауэла
Слайд 146Методы моделирования эволюции
Классические генетические алгоритмы
Генетические микроалгоритмы
Генетические алгоритмы со взаимной эволюцией
Параллельные
эволюционные алгоритмы
Генетические алгоритмы для многокритериальной оптимизации
Слайд 147Методы имитирующие интеллект роя
1. Муравьиный алгоритм (англ. Ant colony optimization).
2. Метод
роя частиц (англ. Particle swarm optimization).
3. Пчелиный алгоритм (англ. Bees algorithm).
4.
Оптимизация передвижением бактерий (англ. Bacterial foraging optimization).5. Стохастический диффузионный поиск (англ. Stochastic diffusion search).
6. Алгоритм гравитационного поиска (англ. Gravitational search algorithm).
7. Алгоритм капель воды (англ. Intelligent Water Drops algorithm).
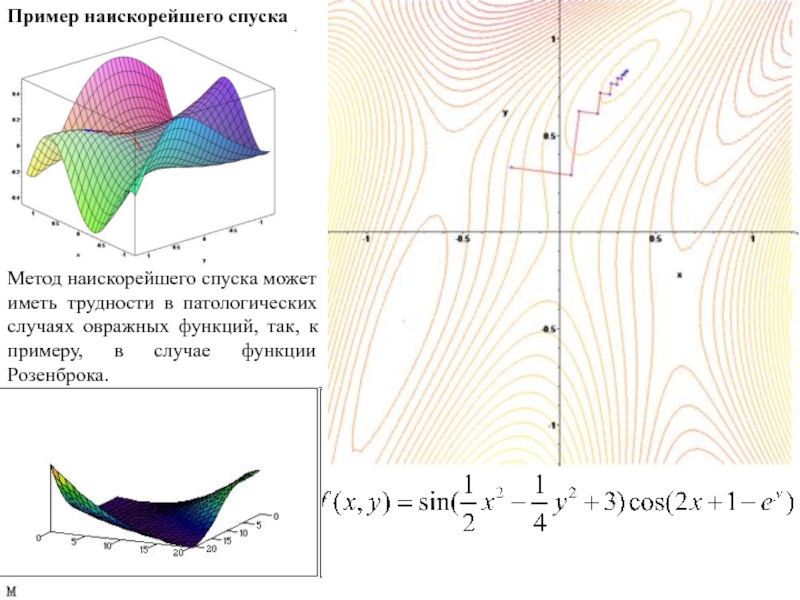
Слайд 150Пример наискорейшего спуска
Метод наискорейшего спуска может иметь трудности в патологических
случаях овражных функций, так, к примеру, в случае функции Розенброка.
Слайд 151Классические генетические алгоритмы
Генетические алгоритмы (ГА) своим существованием обязаны наблюдениям и
испытаниям естественных процессов наследования, происходящих в мире живых организмов, а
именно эволюции и связанной с ней естественной селекции. Идею генетических алгоритмов предложил Джон Генри Холланд на рубеже шестидесятых и семидесятых годов. В 1975 году им была опубликована книга "Adaptation in Natural and Artificial Systems" [Holland, 1975]. Описание ранней истории ГА дано в книге Д. Голдберга "Genetic Algorithms in Search, Optimization and Machine Learning" [Goldberg, 1989].Джон Генри Холланд,
американский ученый, отец генетических алгоритмов
Слайд 152Ученых заинтересовали признаки естественной эволюции, а точнее тот факт, что
эволюция происходит на хромосомах, а не на живых существах. Holland
верил, что введенный в компьютер соответствующий алгоритм, может дать технологию решения трудных проблем по аналогии с природой – через эволюцию. Он работал над алгоритмами, оперирующими с рядами бинарных цифр: нулей и единиц, которые назвал хромосомами. Эти алгоритмы производили имитацию эволюции на популяции хромосом и использовали механизмы селекции или репродукции аналогичные процессам присущим естественной эволюции. Такие же как в природе, эти алгоритмы решали проблемы нахождения "хороших" хромосом, ничего не зная о характере проблемы, которую решали. Единственная имевшаяся в распоряжении компьютера информация, это оценка каждой хромосомы, отражающая ее приспособление.Классические генетические алгоритмы
Слайд 153Рассмотрим оптимизационную задачу. Для системы, представленной на рисунке необходимо определить:
Решение оптимизационной задачи классическим генетическим алгоритмом
Простейшая система управления
Слайд 154Параметры этой задачи - и
. Пространство поиска будет содержать конечное множество точек,
которые можно закодировать индивидуумами. Параметры и - дискретизированы и расположены в пределах отдо в виде соответствующих бинарных кодовых рядов. При этом
соответствует кодовый ряд, состоящий только из нулей, а - кодовый ряд, включающий одни единицы. Длина этих кодовых рядов зависит от значений и , а также от частоты дискретизации интервала
. Предположим, что = -25, а =25 и для параметров , применены 10-ти битовые кодовые ряды. Тогда популяция для данного примера состоит из семи индивидуумов и представлена в табл. 5.14.
Первые десять генов каждого индивидуума соответствуют параметру , а остальные десять - параметру . Длина индивидуума, таким образом, равна 20.
Популяция, хромосомы, гены, генотип, фенотип
Слайд 155Основной, классический генетический алгоритм называют часто также и простым ГА.
Он состоит из следующих шагов: 1) инициализации, т.е. выбора начальной
популяции индивидуумов; 2) оценки приспособленности индивидуумов в популяции; 3) проверки условий остановки; 4) селекции индивидуумов; 5) применения генетических операторов; 6) создания новой популяции; 7) вывода "наилучшего" индивидуума.Блок-схема классического генетического алгоритма
Слайд 156Инициализация - создание начальной популяции. Основано на выборе разыгрыванием заданного
числа хромосом (индивидуумов), представленных бинарными кодами определенной длины.
Оценка приспособленности индивидуумов
в популяции основана на вычислении значения функции оценки для каждого индивидуума их этой популяции. Чем больше значение функции, тем лучше качество индивидуума. Проверка условий останова. Останов ГА может наступать, если дальнейшая его работа уже не изменяет значения искомого экстремума. Алгоритм может останавливаться, по истечении некоторого времени работы или после завершения определенного количества выполненных итераций. Если условие останова выполнено, то наступает переход к последнему шагу, т.е. вывод "наилучшего" индивидуума. Если нет, то следующим шаг - селекция.
Описание блок-схемы классического ГА
Слайд 157Селекция индивидуумов. Основана на выборе, по значениям функции оценки, тех
индивидуумов-родителей, которые будут принимать участие в создании потомков следующего поколения.
Этот выбор проходит по принципу естественной селекции, т.е. наибольший шанс на участие в создании новых индивидуумов имеют индивидуумы с наибольшими значениями функции оценки. Существует много методов селекции. Наиболее популярный из них – метод рулетки. Суть его состоит в том, что каждому индивидууму ставится в соответствие сектор колеса рулетки со значением пропорциональным значению функции оценки данного индивидуума. Чем больше это значение, тем больше размер сектора на колесе рулетки. Все колесо рулетки соответствует сумме значений функции оценки всех индивидуумов из популяции для решения данной задачи. Каждому индивидууму, обозначенному , где N - численность популяции, соответствует сектор , представляющий собой часть всего колеса, выраженную в процентах:При этом обозначает значение функции оценки индивидуума , а - вероятность выбора индивидуума .
Описание блок-схемы классического ГА
Слайд 158Выбор индивидуума - следствие оборота колеса рулетки. В результате "выигрывает"
индивидуум, лежащий в разыгранном этим способами секторе колеса рулетки. Очевидно
этот сектор тем больше, чем больше значение функции оценки. Если вся окружность колеса рулетки будет трактоваться как интервал чисел [0,100], то разыгрывание индивидуума можно трактовать как разыгрывание числа из интервала [a, b], где a и b обозначают, соответственно, начало и конец фрагмента круга соответствующего этому сектору колеса. Очевидно, что . Тогда разыгрывание с помощью колеса рулетки сводится к разыгрыванию числа из интервала [0,100], которое соответствует конкретной точке на окружности колеса рулетки.В результате селекции создается родительская популяция из индивидуумов, называемая родительской пулой. Она и становится текущей популяцией на очередном шаге работы алгоритма.
Описание блок-схемы классического ГА
Слайд 159Применение генетических операторов. Применение генетических операторов к индивидуумам, отобранным методом
селекции, используется для создания новой популяции потомков. В классическом ГА
применяются два основных генетических оператора: скрещивания (англ. crossover) и мутации (англ. mutation). Последний играет второплановую роль по сравнению с оператором скрещивания. Это означает, что в классическом ГА скрещивание происходит почти всегда, в то время как мутация - достаточно редкое явление. Вероятность скрещивания принимается обычно достаточно большой ( ), а вероятность мутации маленькой ( ). Это соответствует эволюции в живой природе, где мутация чрезвычайно редкое явление.Описание блок-схемы классического ГА
Слайд 160Оператор скрещивания. Первый этап скрещивания - выбор пар из родительской
пулы. На этом этапе индивидуумы из родительской популяции сочетаются
в пары. Выбор пары происходит случайно, в соответствии с вероятностью скрещивания . Далее, для каждой пары выбранных этим способом родителей, разыгрывается позиция гена, определяющая так называемую точку скрещивания. Если индивидуумы-родители состоят из L генов, то, очевидно, точку скрещиванияможно разыграть как значение случайного числа равномерно распределенного на интервале [1, L -1]. В результате скрещивания пары родителей получается пара потомков по следующему правилу: 1) один потомок складывается из генов на позициях от 1 до , взятых от первого родителя и остальных генов, от позиции
+1 до L , взятых от второго родителя; 2) второй потомок складывается из генов на позициях от 1 до , взятых от второго родителя и остальных генов, от позиции +1 до L, взятых от первого родителя.
Описание блок-схемы классического ГА
Слайд 161Оператор мутации. В соответствии с вероятностью мутации, значение гена индивидуума
изменяется на противоположное (0 → 1 или 1 → 0).
Например, если в индивидууме [100110101010] мутации подвергся ген на позиции 7, то получим следующую хромосому [100110001010]. Вероятность мутации очень мала и возникает в соответствии с задаваемой пользователем вероятностью мутации. Тогда для каждого гена разыгрывается случайное число из интервала [0,1] и, если СЧ , то ген мутирует.
Создание новой популяции. Индивидуумы получаемые генетическими операторами из индивидуумов родительской популяции формируют текущую популяцию для новой итерации ГА. В классическом ГА вся предыдущая популяции индивидуумов заменяется на новую популяцию потомков той же самой численности.
Вывод "наилучшего" индивидуума. Если выполнено условие останова алгоритма, необходимо вывести результат. Наилучшее решение задачи - индивидуум с наибольшим значением функции оценки в популяции.
Описание блок-схемы классического ГА
Слайд 162Возьмем упрощенный и немного искусственный пример, нахождения индивидуума с возможно
большим числом единиц. Предположим, что индивидуум состоит из 12 генов,
а популяция содержит 8 индивидуумов. Известно, что наилучшим будет индивидуум из 12 единиц. Рассмотрим поэтапно решение этой тривиальной задачи с помощью ГА.Инициализация. Генерируем восемь бинарных кодов с длиной равной 12 и тем самым получаем начальную популяцию:
= [111001100101],
=[010001100100],
= [001100111010],
=[010011000101],
=[011101110011],
=[101011011011],
= [001000101000],
= [000010111100].
Пример работы классического ГА
Слайд 163Оценка приспосабливаемости индивидуумов в популяции. Значения функции оценки равны числу
единиц в индивидууме. Обозначим функцию оценки через
. Тогда ее значения для хромосом в начальной популяции даны ниже:Индивидуумы характеризуются наибольшими значениями функции оценки. В этой популяции они наилучшие кандидаты на то, что быть решениями задачи. Поскольку условие останова не выполнено, то следующий шаг - селекция индивидуумов в текущей популяции.
Пример работы классического ГА
Слайд 164Селекция. Выполним селекцию методом рулетки. Для каждой из восьми хромосом
текущей популяции (N = 8) имеем сектора колеса рулетки, выраженные
в процентах:= 15,2 ,
= 13,0 ,
= 17,4 ,
= 6,5 ,
= 8,7 ,
= 10,9 ,
= 17,4 ,
= 10,9 .
Далее пусть было разыграно восемь чисел: 79, 44, 9, 74, 44, 86, 48, 23. Это означает выбор для репродукции индивидуумов:
Индивидуум был выбран три раза, а два раза. Все выбранные индивидуумы входят в родительскую пулу.
Пример работы классического ГА
Слайд 165Применение генетических операторов. Предположим, что множество индивидуумов, разыгранных с помощью
оператора селекции, не мутируют, а подлежат скрещиванию. Это означает, что
вероятность скрещивания , а вероятность мутации . Предположим, что среди индивидуумов , , , , , , , разыгрыванием выбраны следующие пары родителей:(и) , (и) , (и) , (и) , а для пар разыграны точки скрещивания , , , , соответственно. Тогда скрещивание будет выполнено в соответствии с рисунком и в результате имеем четыре пары потомков.
Пример работы классического ГА
Слайд 166Создание новой популяции. После скрещивания имеем следующую текущую популяцию потомков:
= [011101110010],
= [101000111010],
= [001000101001],
= [111011011011],
= [011101011011],
= [101001100101],
= [101011110011].
Чтобы отличить индивидуумов предыдущей популяции от индивидуумов новой популяции, последние обозначены звездочками.
Далее, в соответствии с блок-схемой ГА, выполняется шаг 2, т.е. оценка приспосабливаемости членов новой популяции, которая становится текущей. Значения функции оценки для этой популяции следующие: = 8, = 6,
= 9, = 6, = 7, = 4, = 8, = 8.
Как видно, популяция потомков теперь характеризуется много большим средним значением функции оценки, чем популяция родителей. Предположим, что в результате скрещивания найден индивидуум с наибольшим значением функции оценки, которого не имел ни один из родителей. Чтобы не продолжать итерации, пусть и станет решением задачи.
Пример работы классического ГА
Слайд 168Основы теории массового обслуживания
Большинство систем, с которыми человек имеет дело
- стохастические. Попытка их математического описания с помощью детерминистических моделей
приводит к огрублению истинного положения вещей. При решении задач анализа и проектирования таких систем приходится считаться с тем, что случайность является определяющей для процессов, протекающих в системах. При этом пренебрежение случайностью, попытка “втиснуть” решение перечисленных задач в детерминистические рамки приводит к искажению, к ошибкам в выводах и практических рекомендациях.Первые задачи теории систем массового обслуживания (ТМО) были рассмотрены сотрудником Копенгагенской телефонной компании, датским ученым А.К. Эрлангом в период между 1908 и 1922гг. Эти задачи были вызваны к жизни стремлением упорядочить работу телефонной сети и разработать методы, позволяющие заранее повысить качество обслуживания потребителей в зависимости от числа используемых устройств. Оказалось, что ситуации, на телефонных станциях – типичные и для аэродромов, морских и речных портов, магазинов, терминальных классов, электронных вычислительных комплексов, радиолокационных станций и т.д. могут быть описаны в рамках ТМО.
Примерно 80 % всех систем – это системы массового обслуживания.
Слайд 169Пример 1. Телефонная связь времен Эрланга представляла из себя телефонную станцию,
связанную с большим числом абонентов. Телефонистки станции по мере поступления
вызовов соединяли телефонные номера между собой.Задача: Какое количество телефонисток (при условии их полной занятости) должно работать на станции для того, чтобы потери требований были минимальными.
Пример 2. Система скорой помощи некоего городского района представляет собой пункт (который принимает требования на выполнение), некоторое количество автомашин скорой помощи и несколько врачебных бригад.
Задача: Определить количество врачей, вспомогательного персонала, автомашин, для того чтобы время ожидания вызова было для больных оптимальным при условии минимизации затрат на эксплуатацию системы и максимизации качества обслуживания.
Пример 3. Важной задачей является организация морских и речных перевозок грузов. При этом особое значение имеют оптимальное использование судов и портовых сооружений.
Задача: Обеспечить определенный объем перевозок при минимальных расходах. При этом сократить простои судов при погрузочно-разгрузочных работах.
Основы теории массового обслуживания
Слайд 170- Случайная величина «Интервал между приходами двух очередных заявок»
- Случайная
величина «Время обслуживания заявки прибором»
Понятие СМО
Слайд 171
Потоком называют последовательность событий. Поток, состоящий из требований на обслуживание,
называют потоком требований.
Поток требований, поступающих в обслуживающую систему, называют входящим
потоком.Поток требований, которые обслужены, называют выходящим потоком.
Совокупность очередей и приборов (каналов) обслуживания называются системой обслуживания.
Каждые требования поступают на свой канал, где подвергается операции обслуживания.
Каждая СМО имеет определенные правила формирования очереди и правила или дисциплину обслуживания.
Определения, термины
Слайд 172СМО различают:
По дисциплине обслуживания:
обслуживание в порядке поступления;
обслуживание в случайном порядке
(в соответствии с заданным законом распределения);
обслуживание с приоритетом.
По характеру организации:
с
отказами;с ожиданиями в очереди;
По количеству обслуживающих приборов:
одноканальные;
многоканальные.
Классификация СМО
Слайд 173Основная задача ТМО - установление зависимости между характером потока заявок
на входе СМО, производительностью одного канала, числом каналов и эффективностью
обслуживания.В качестве критерия эффективности могут быть использованы различные функции и величины:
среднее время простоя системы;
среднее время ожидания в очереди;
закон распределения длительности ожидания требования в очереди;
средний % заявок, получивших отказ; и т.д.
Современная ТМО является совокупностью аналитических методов исследования перечисленных разновидностей СМО.
Основная задача теории массового обслуживания
Слайд 174Входящий поток
Выходящий поток
Очередь
Обслуживающий прибор (канал)
Модель одноканальной экспоненциальной СМО
Одноканальная система массового
обслуживания (СМО) задается следующими свойствами. СМО имеет канал. В СМО приходят заявки.
Если СМО пустая (нет заявок), то приходящая заявка занимает канал. Заявка, приходящая в непустую СМО (канал занят), становится в очередь к каналу. Любая заявка, занявшая канал, обслуживается, освобождает канал и уходит из СМО. Если в момент ухода очередь не пустая, то первая в ней заявка выходит из очереди и занимает канал.Слайд 176Цель анализа СМО заключается в расчете ее характеристик, важнейшие из
которых следующие:
- коэффициент загрузки ρ;
- средняя длина очереди L ;
-
среднее число заявок в СМО M ;- среднее время ожидания обслуживания W;
- среднее время пребывания заявки в СМО U.
Пуассоновский поток событий
Цель анализа СМО
Слайд 177Коэффициент загрузки рассчитывается по формуле:
Если выполняется условие ρ ≤ 1 («физический смысл»
этого требования состоит в том, чтобы «скорость поступления работы» в
систему не превышала «скорости ее выполнения» системой), то существует стационарный режим функционирования СМО. В стационарном режиме такие вероятностные характеристики происходящих в СМО процессов, как L, М, W, U не зависят от времени, т.е. являются постоянными величинами. Сами происходящие в СМО процессы остаются при этом случайными.Расчет коэффициента загрузки СМО
Слайд 178В стационарном режиме среднее число M заявок в СМО постоянно. Поэтому среднее число заявок,
поступающих в СМО в единицу времени, равно среднему числу заявок,
в единицу времени из СМО уходящих.Следовательно, в стационарном режиме интенсивность потока уходящих заявок равна λ. Эта величина меньше, чем интенсивность обслуживания μ, т.к. канал в стационарном режиме определенную долю времени простаивает. Эта доля времени равна (1-ρ) - коэффициенту простоя СМО.
Интенсивность выходного потока заявок равна интенсивности обслуживания, когда канал занят, и равна нулю, когда канал свободен. В среднем же она равна интенсивности поступления заявок. Поэтому среднее число заявок в СМО в стационарном режиме со временем не изменяется, остается постоянным.
Расчет коэффициента загрузки СМО
Слайд 179Коэффициент загрузки ρ в стационарном режиме можно интерпретировать следующими способами:
а) как среднее
значение той части единицы времени, в течение которой канал занят;
б)
как вероятность застать канал занятым при обращении к нему в случайный момент времени;в) как среднее число заявок в канале.
В экспоненциальной СМО, коэффициент загрузки равен также вероятности того, что приходящая в СМО заявка застанет канал занятым.
Далее рассматриваем только стационарные значения характеристик.
Средняя длина очереди L (среднее число заявок в очереди) в одноканальной экспоненциальной СМО рассчитывается по формуле:
График зависимости L(ρ) приведен на рисунке. Среднее число M заявок в СМО равно сумме среднего числа L заявок в очереди и среднего числа r заявок в канале:
где r - среднее число заявок в канале.
Средняя длина очереди
Слайд 181Применяя формулу Литтла к очереди в СМО, находим среднее время
ожидания обслуживания через среднюю длину очереди:
Аналогично вычисляется среднее время
пребывания заявки во всей СМО:Если учесть, что время прохождения заявки через СМО складывается из времени ее прохождения через очередь и времени обслуживания в канале, то величину U можно вычислить и как сумму соответствующих средних времен:
Применение формулы Литтла