Слайд 1Самарский Энергетический Колледж
Логарифмы.
Руководитель:к.п.н.,доцент
Т.Н.Андрюхина
Студент:11 Т
Козлов.С.А
Самара 2016
Слайд 2Содержание
1.Что такое логарифм?
2.Виды логарифм.
3.Практические применения
3.1:Физика, астрономия, химия.
3.2:Музыка, сейсмология,
магнитуда землетрясения.
3.3:Логарифмическая спираль.
4.История логарифм.
4.1: Возникновение логарифм.
4.2:Логарифмы
с основанием.
4.3: Джон Непер.
Слайд 3Определение логарифма
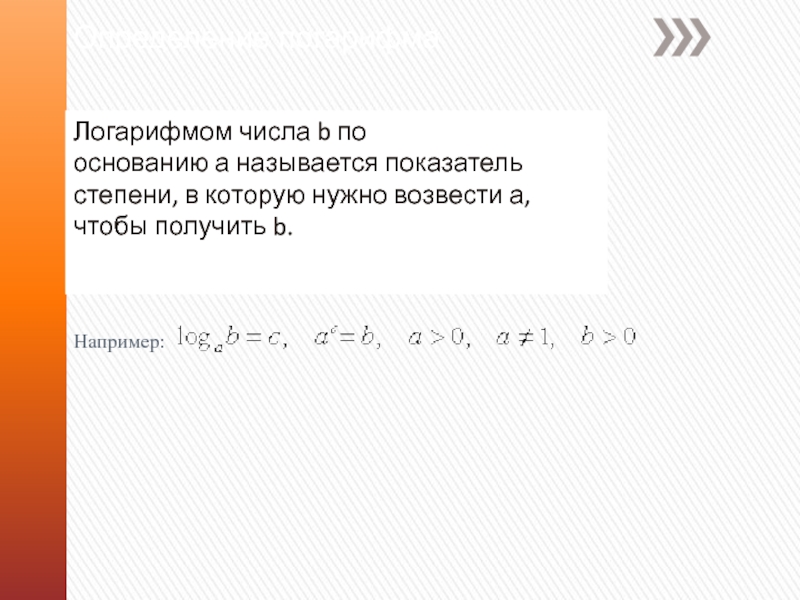
Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести а,
чтобы получить b.
Например:
Слайд 4Виды логарифм
loga b - логарифм числа b по основанию a (a > 0, a ≠ 1, b > 0)
lg b - десятичный логарифм (логарифм по
основанию 10, a = 10).
ln b - натуральный логарифм (логарифм по основанию e, a = e).
Слайд 5Практическое применение
Физика — интенсивность звука (децибелы), оценивается также уровнем интенсивности по
шкале децибел;
число децибел N=10lg(I/I0), где I — интенсивность данного звука.
Астрономия
Если
известна видимая звёздная величина и расстояние до объекта, можно вычислить абсолютную звёздную величину по формуле:
Химия
Водородный показатель, "pH ", — это мера активности ионов водорода в растворе, количественно выражающая его кислотность, вычисляется как отрицательный десятичный логарифм концентрации водородных ионов, выраженной в молях на литр:
mbox{pH} = -lg left [ mbox{H}+ ight]
Слайд 6Практическое применение
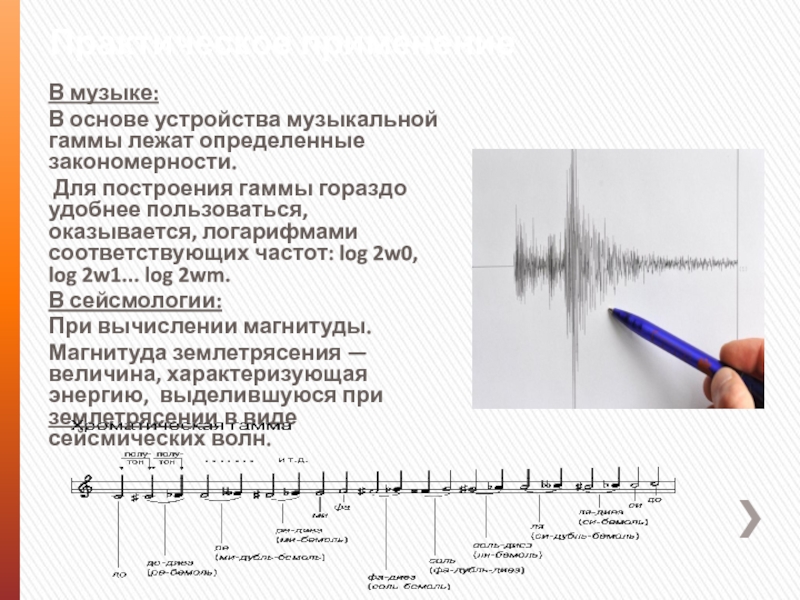
В музыке:
В основе устройства музыкальной гаммы лежат определенные закономерности.
Для построения гаммы гораздо удобнее пользоваться, оказывается, логарифмами соответствующих частот:
log 2w0, log 2w1... log 2wm.
В сейсмологии:
При вычислении магнитуды.
Магнитуда землетрясения — величина, характеризующая энергию, выделившуюся при землетрясении в виде сейсмических волн.
Слайд 7Практическое применение
Логарифмическая спираль.
Логарифмическая спираль является траекторией точки, которая движется вдоль
равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному
расстоянию. Точнее, в логарифмической спирали углу поворота пропорционален логарифм этого расстояния.
Слайд 8История возникновения логарифм
Логарифмы возникли в 16 веке в связи с необходимостью
проведения большого объема приближенных вычислений в ходе решения практических задач,
и в первую очередь задач астрономии.
В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной.
Слайд 9Логарифмы с основанием
Логарифмы с основанием ввел учитель математики Спейдел. Слово основание
заимствовано из теории о степенях и перенесено в теорию логарифмов
Эйлером. Глагол “логарифмировать” появился в 19 веке у Коппе. Коши первый предложил ввести различные знаки для десятичных и натуральных логарифмов. Обозначения, близкие к современным ввел немецкий математик Прингсхейм в 1893 году. Именно он обозначал логарифм натурального числа через ln. Определение логарифма как показателя степени данного основания можно найти у Валлиса (1665 год), Бернулли (1694 год).
Слайд 10Джон Непер
В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение
под названием «Описание удивительной таблицы логарифмов» (лат. Mirifici Logarithmorum Canonis Descriptio). В нём
было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1’. Термин логарифм, предложенный Непером, утвердился в науке.
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
Слайд 11Леонард Эйлер
Близкое к современному понимание логарифмирования — как операции, обратной возведению
в степень — впервые появилось у Валлиса и Иоганна Бернулли,
а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Слайд 12Заключение
Логарифмы- это то, что окружает нас и даёт понятие в
разных областях жизни , науки и техники.
В большей своей части
они нужны инженерам , техникам, учёным чтобы сократить вычисления до минимума и дать более полную картину какого либо явления.
Слайд 13Используемые источники:
http://tatynavlasova.tumblr.com
История логарифмов
http://www.webmath.ru
Математические формулы
https://ru.wikipedia.org
Раздел:логарифмы