Сечения многогранников

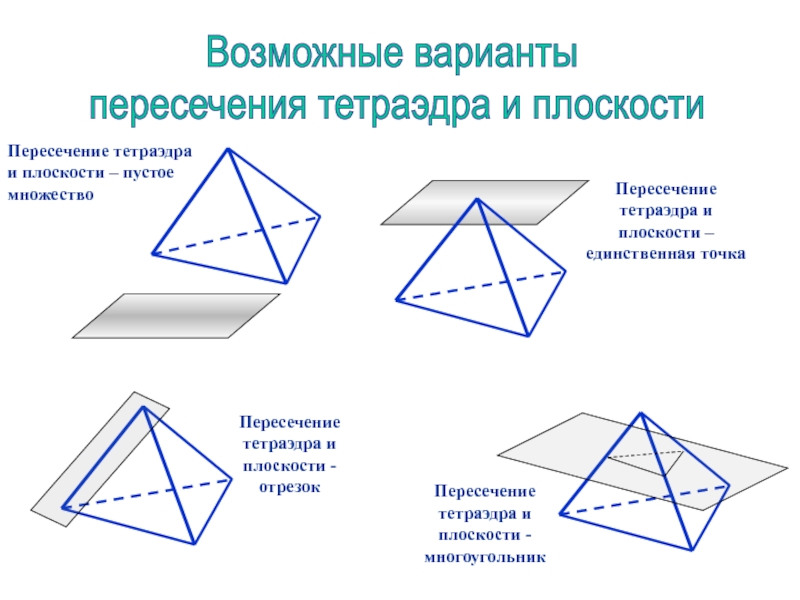
пустое множество
Пересечение тетраэдра и плоскости – единственная точка
Пересечение тетраэдра и

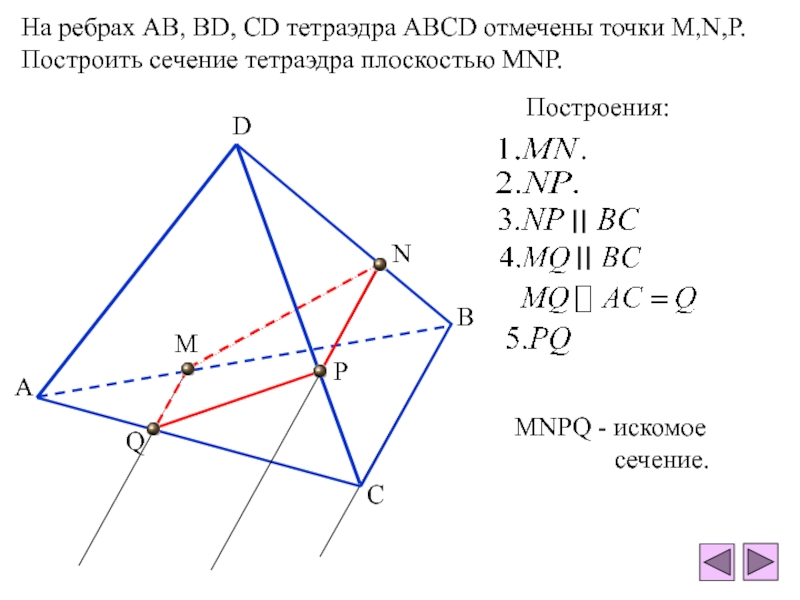
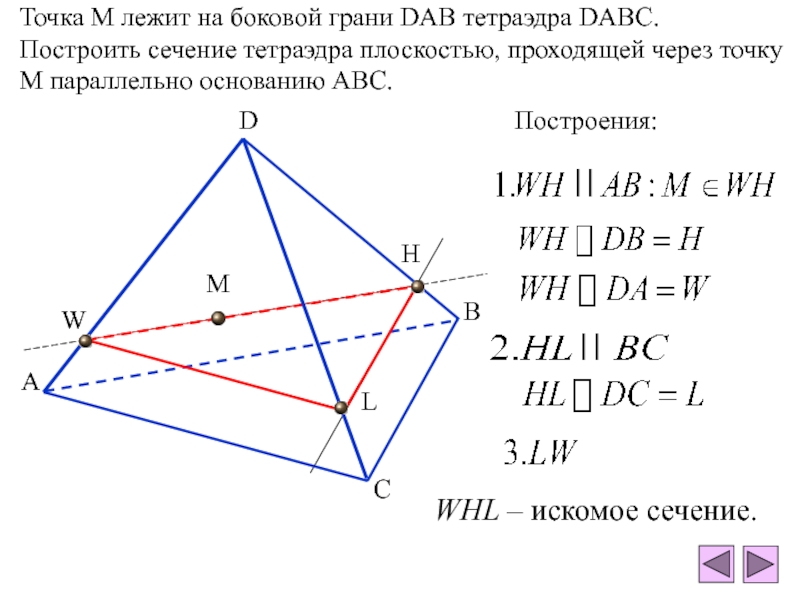
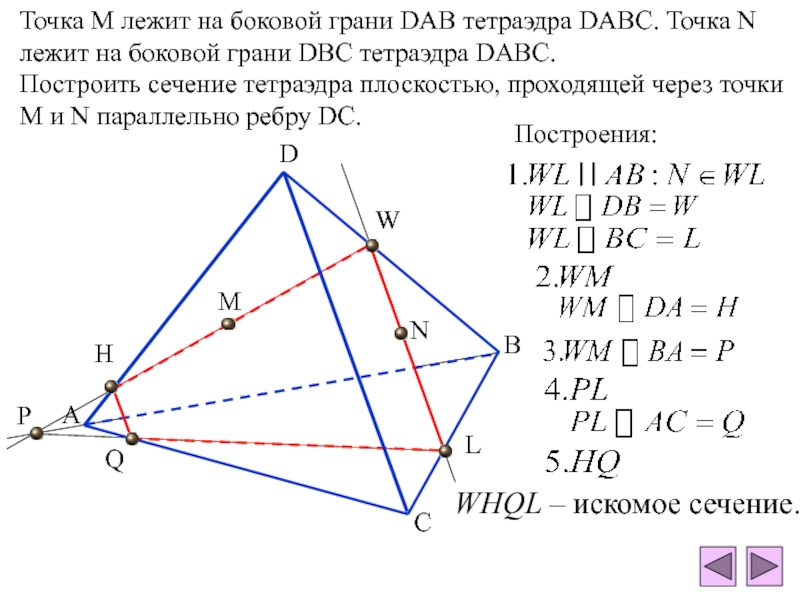
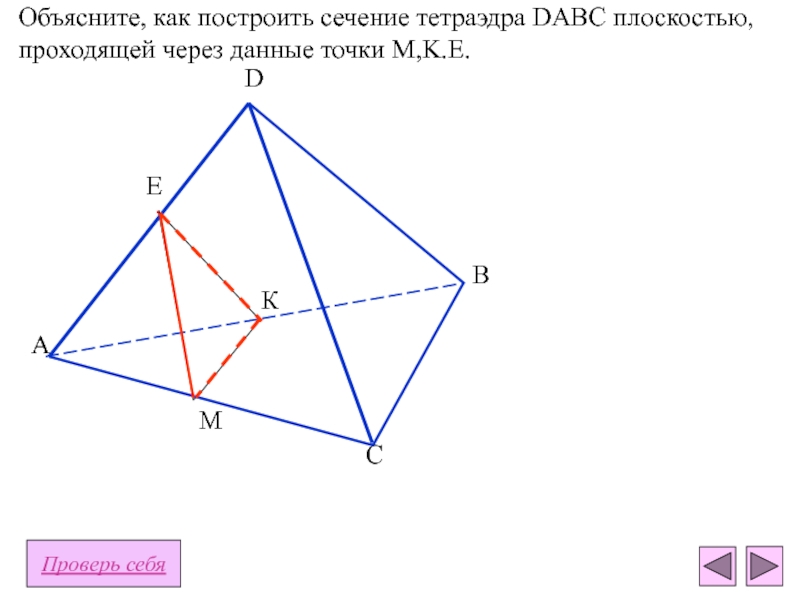
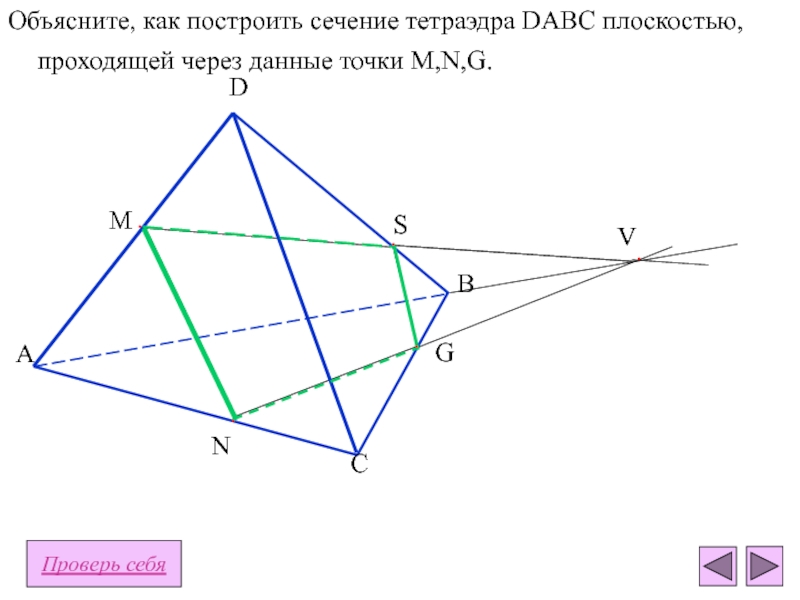
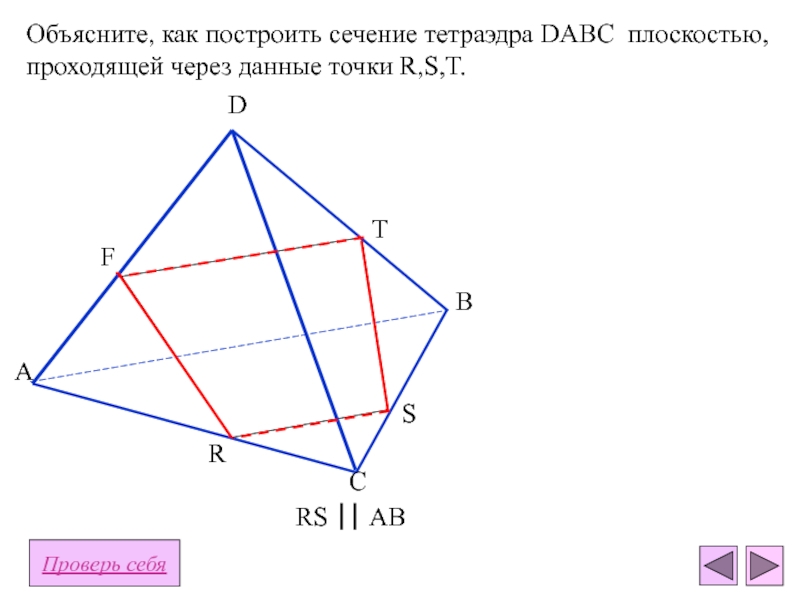
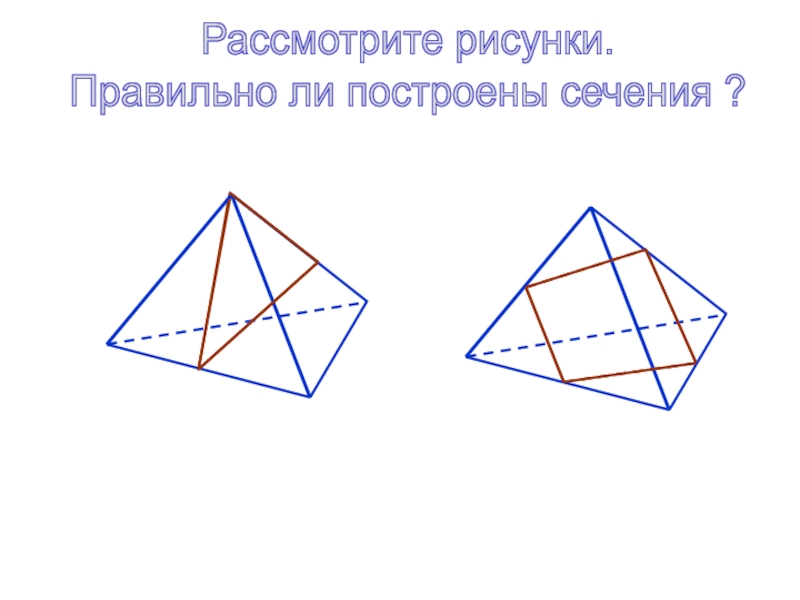
Пересечение тетраэдра и плоскости - многоугольник

от которой имеются точки данного тетраэдра.
R
S
T
Сечением тетраэдра

Сечение тетраэдра- выпуклый
многоугольник , вершинами которого являются точки
пересечения секущей плос-
кости с ребрами тетраэдра, а сторонами - линии пересече-ния секущей плоскости с его гранями.

граней тетраэдра.
Найти две точки этой прямой, принадлежащие одной грани.
Воспользоваться

2.Точка пересечения прямой с плоскостью отыскивается как точка пересечения известной прямой, лежащей в одной плоскости, с прямой, которая является общей для двух рассматриваемых плоскостей.

3.Воспользоваться утверждением №1 из свойств параллельности прямой и плоскости

прямой, лежащей в одной плоскости, с прямой, которая является общей

прямой, лежащей в одной плоскости, с прямой, которая является общей

прямой, лежащей в одной плоскости, с прямой, которая является общей

многогранника, и провести через них прямую.
Выделить отрезок, принадлежащий сечению.
Выбрать

План построения сечений.

сечение тетраэдра плоскостью MNP.

Построения:
1. NP (т.к. N и P

2. NM (т.к. N и M лежат в одной грани )

3. PM (т.к. P и M лежат в одной грани )

сечение тетраэдра плоскостью MNP.
Построения:
MNPQ - искомое

сечение.
На ребрах AB, BD, CD тетраэдра ABCD отмечены

тетраэдра плоскостью, проходящей через точку
М параллельно основанию ABC.
Построения:
WHL – искомое

N лежит на боковой грани DBC тетраэдра DABC.
Построить сечение тетраэдра

Построения:

WHQL – искомое сечение.

точки M,K.E.
А
D
B
C
Е
М
К



Проверь себя

данные точки R,S,T.
RS
AB

Проверь себя