Слайд 1Shrnutí minulé přednášky
Regresní analýza (průběh) – lineární regresní funkce
Korelační analýza
(těsnost závislosti)
x …..nezávisle proměnná
y …..závisle proměnná
, ..neznámé parametry v
ZS
a, b ..neznámé parametry v VS
Bodové odhady a, b parametrů ,
se z pozorovaných dat nejčastěji získávají
metodou nejmenších čtverců.
Populační korelační koeficient ρ
Výběrový korelační koeficient r
Слайд 2Testování
regresních a korelačních charakteristik
Слайд 3Testování hypotéz
Podstatné testy významnosti v korelační a regresní analýze
● test významnosti korelačního koeficientu
● test významnosti
jednotlivých regresních
parametrů
● test významnosti regresního modelu jako celku
Слайд 4Testování Pearsonova korelačního koeficientu
Hypotéza předpokládá, že korelace neexistuje,
tzn. veličiny
X a Y jsou nezávislé.
H0: = 0
Alternativní hypotéza
je postavena na existenci
korelace.
H1: 0
Слайд 5Testování Pearsonova korelačního koeficientu
Test hypotézy se provádí pomocí testového
kritéria
V případě, že vypočtená hodnota testového kritéria
padne do kritického oboru,
zamítá se nulová
hypotéza a existence lineární korelační závislosti
se považuje za prokázanou.
se zamítá na
Слайд 6Testování Spearmanova koeficientu pořadové korelace
H0: s = 0
H1: s
0
Testování se provádí pomocí tabulek (tab. 22)
> r0,05(9)
= 0,602
< r0,01(9) = 0,735
Spearmanův korelační koeficient je statisticky významný na 5% hladině významnosti.
Слайд 7Testování regresního koeficientu
Test významnosti nulové hypotézy
vychází ze skutečnosti, že regresní koeficient je roven 0
(přímka nemá směrnici, je statisticky nevýznamná).
H0: = 0
H1: 0
Слайд 8Testování regresního koeficientu
Test hypotézy se provádí pomocí testového kritéria
se zamítá na
V případě, že se zamítá H0, je existence lineární
závislosti prokázána.
Слайд 9Test regresního modelu
Test významnosti celé regresní přímky (modelu)
se provádí
pomocí upravené jednoduché ANOVY.
V případě lineární regresní funkce je závěr
testů
významnosti celého regresního modelu shodný
(ekvivalentní) s testem regresního koeficientu!!!
Pro rovnici s jedním prediktorem F = t2
Слайд 10Test regresního modelu
Testujeme nulovou hypotézu o nulovosti všech
regresních koeficientů.
H0: všechna b = 0
H1: non H0
Jestliže F > F zamítáme H0 na
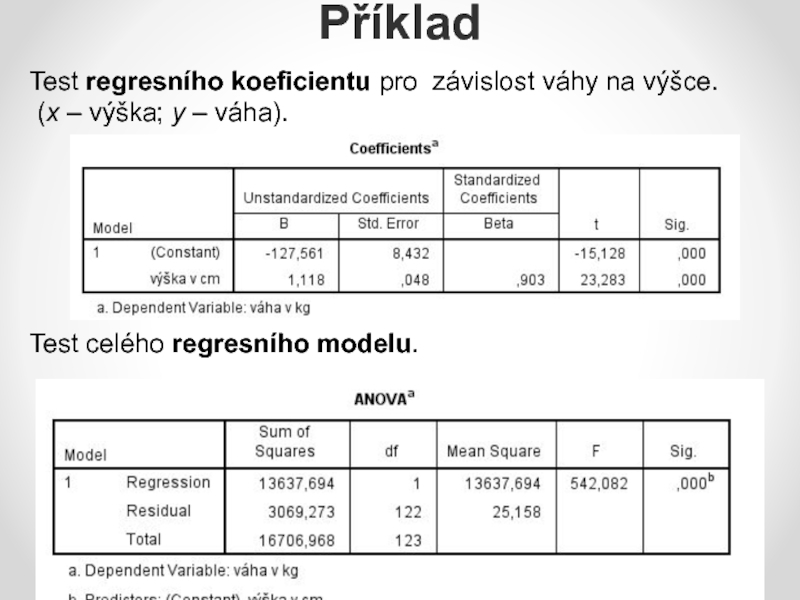
Слайд 11Příklad
Test regresního koeficientu pro závislost váhy na výšce.
(x –
výška; y – váha).
Test celého regresního modelu.
Слайд 12Odhad
regresních a korelačních charakteristik
Слайд 13Korelační charakteristiky
Bodový odhad populačního korelačního koeficientu
Intervalový odhad populačního
korelačního koeficientu
Postup výpočtu záleží na rozsahu výběrového souboru
Слайд 14Korelační charakteristiky
Intervalový odhad korelačního koeficientu
V případě, že výběrový
soubor má dostatečně velký rozsah (n > 100), lze rozdělení
výběrového korelačního koeficientu aproximovat normálním rozdělením.
Oboustranný interval spolehlivosti
Слайд 15Korelační charakteristiky
Intervalový odhad korelačního koeficientu
V případě, že výběrový
soubor má rozsah n < 100, provádíme Fisherovu Z- transformaci.
r Z a zpětně inverzní transformaci Z r
Oboustranný interval spolehlivosti pro Z
Převody hodnot provádíme pomocí tabulek.
Слайд 16Příklad
Intervalový odhad populačního korelačního koeficientu ρ
n = 15, r =
0,9322
Z – transformace (tab. 16.1) r = 0,9322 → Z
= 1,6584
P ( 1,0925 Z 2,2243) = 0,95
Zpětná (inverzní) transformace (tab. 16.2)
Z = 1,0925 → r = 0,7969
Z = 2,2243 → r = 0,9767
P ( 0,7969 ρ 0,9767) = 0,95
Слайд 17Regresní charakteristiky
Bodový odhad regresního koeficientu získáváme
pomocí metody nejmenších čtverců tzn.
Oboustranný
interval spolehlivosti pro regresní
koeficient je vymezen následujícím vztahem
Слайд 18Příklad
Oboustranný interval spolehlivosti regresního
koeficientu pro závislost váhy na výšce
Слайд 19Regresní přímka
Výběrovou regresní přímku můžeme využít:
1) Pro odhad podmíněné střední
hodnoty závislé veličiny y odpovídající určité konkrétní hodnotě nezávislé veličiny
xi.
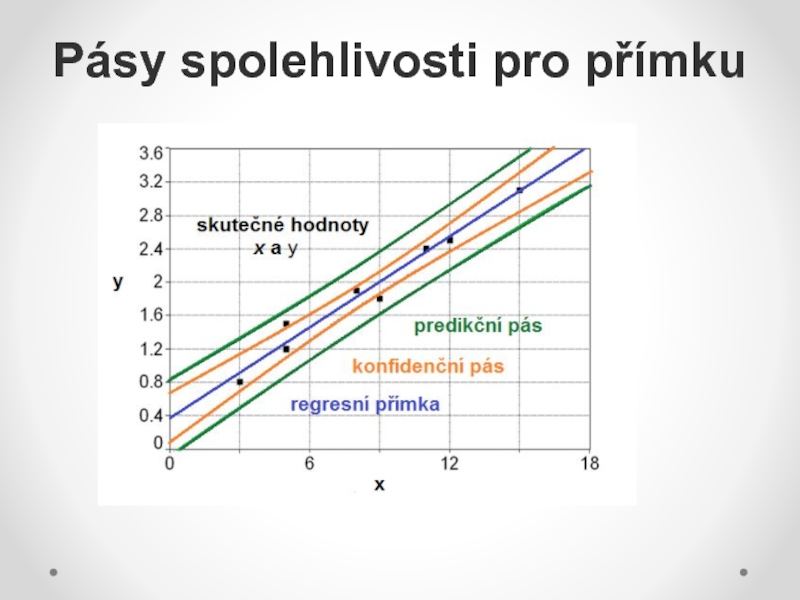
Konfidenční pás pro přímku
2) Pro předpověď individuální hodnoty veličiny y´ odpovídající určité hodnotě nezávislé veličiny xi.
Predikční pás pro jednotlivá pozorování
Слайд 21Shrnutí přednášky
Podstatou řešení regresní analýzy je:
stanovit nejvhodnější tvar regresního modelu
(tedy určit příslušnou rovnici, která bude popisovat závislost y na
x),
stanovit jeho parametry (tj. stanovit konkrétní hodnoty parametrů ),
stanovit statistickou významnost parametru a celého modelu (tj. zda model podstatným způsobem přispěje ke zpřesnění odhadu závisle proměnné),
výsledky dané modelem interpretovat z hlediska zadání.