Слайд 1Система одновременных уравнений
Слайд 2Системы уравнений в эконометрике
Для изучения комплексных экономических явлений средствами эконометрики,
как правило, применяют не отдельные уравнения регрессии, а системы уравнений.
Это объясняется следующим.
Описывая явление с помощью взаимосвязанных переменных, приходится учитывать, что изменение одной переменной влечет за собой изменение других. При рассмотрении же отдельного регрессионного уравнения часто предполагают, что объясняющие переменные можно изменять независимо одну от другой.
Слайд 3Взаимодействие переменных нередко затрудняет однозначную их классификацию при построении модели:
одну и ту же переменную можно определить как объясняющую (фактор)
и как объясняемую (результат).
Слайд 5Система независимых уравнений
Каждый результативный признак (объясняемая переменная) yj, где j=1…n,
является функцией одной и той же совокупности факторов (объясняющих переменных)
xi, i=1..m.
Набор факторов в каждом уравнении системы может варьироваться в зависимости от изучаемого явления.
Слайд 7Система рекурсивных уравнений
Результативный признак yj, где j=1…n, одного уравнения системы
в каждом последующем уравнении является фактором наряду с одной и
той же совокупностью факторов xi, i=1..m.
Слайд 9Система одновременных уравнений
Результативный признак yj, где j=1…n, одного уравнения системы
входит во все другие уравнения системы в качестве фактора наряду
с одной и той же совокупностью факторов xi, i=1..m.
Слайд 11Систему независимых или рекурсивных уравнений решают с помощью МНК.
Для решения
системы одновременных уравнений требуются другие, отличные от МНК методы.
Их
применение обусловлено тем, что результативный признак одного уравнения системы в другом уравнении этой системы используется в качестве фактора и будет коррелировать с соответствующей ошибкой.
Слайд 12Модели системы одновременных уравнений и их составляющие
Слайд 13Основными составляющими обеих форм записи являются эндогенные и экзогенные переменные.
Предполагается,
что экзогенные переменные не коррелируют с ошибкой в соответствующем уравнении.
Структурная
форма
модели
Структурная форма модели
Слайд 14Содержание параметров структурной формы модели
i (i =1..n) - случайная составляющая
(ошибка) i–го уравнения структурной формы модели.
Слайд 15 Если в структурной форме модели переменные yi и xi
(i =1..n, j=1…m) являются отклонениями от среднего уровня y и
x соответственно, то в каждом уравнении системы свободный член не записывается.
Структурная форма модели отражает реальный экономический объект или явление и показывает, как изменение любой экзогенной переменной определяет значения эндогенной переменной.
Наряду с регрессионными уравнениями в модели могут быть записаны и тождества. Таким образом, структурные уравнения модели разделятся на два класса.
Слайд 16Классы структурных уравнений модели
Слайд 17Применение систем одновременных уравнений
Исследование спроса и предложения
Макроэкономическое моделирование механизмов функционирования
экономики на примере конкретной страны
Анализ функций издержек и производственных функций
Слайд 18Модель 1. Предложение и спрос на рынке
Где y1t – спрос
на товар в момент времени t;
y2t
– предложение количества товара в момент t;
y3t – цена, по которой заключаются сделки в моменте t.
Эндогенные переменные
Слайд 19Модель 2. Предложение и спрос кейнсианского типа
Где y1t – спрос
на товар в момент времени t;
y2t
– предложение товара в момент t;
y3t – цена товара в момент t;
y3,t-1 – цена товара в момент (t-1);
x1t – доход в момент t;
t – текущий период;
(t – 1) – предыдущий период;
Эндогенные переменные
Предопределенные переменные
Слайд 20Приведенная форма модели
Приведенная
форма модели
Структурная форма модели может быть преобразована в
приведенную форму.
Слайд 21Содержание параметров приведенной формы модели
i (i =1..n) - случайная составляющая
(ошибка) i–го уравнения приведенной формы модели.
Слайд 22Причины, по которым наряду со структурной формой модели строят ее
приведенную форму
Оценки параметров структурной формы модели, найденные с помощью МНК,
являются смещенными и несостоятельными (нарушаются предпосылки МНК) в силу того, что эндогенные переменные, как правило, коррелируют со случайным отклонением.
Независимость уравнений в приведенной форме модели позволяет определять состоятельные оценки ее параметров с помощью МНК.
Параметры (коэффициенты) приведенной формы модели связаны с параметрами ее структурной формы.
Слайд 23Решение проблемы идентификации
Идентификация
установление соответствия между приведенной и структурной формами модели
Слайд 25Установление неидентифицируемости (сверхидентифицируемости) модели
В идентифицируемой модели количество структурных и приведенных
коэффициентов одинаково.
Если структурных коэффициентов больше (меньше), чем приведенных, то модель
соответственно неидентифицируема (сверхидентифицируема).
Проверка структурной модели на идентифицируемость позволяет установить степень возможности оценивания коэффициентов структурных уравнений по коэффициентам приведенных уравнений.
Слайд 26Необходимое и достаточное условие идентифицируемости уравнения системы
Необходимое условие: n=p+1. Уравнение
модели идентифицируемо, если количество (n) эндогенных переменных этого уравнения на
единицу больше количества (p) предопределенных переменных системы, не входящих в данное уравнение.
Достаточное условие: *0, rang А* = n-1. Если определитель (*) матрицы коэффициентов (А*) при переменных системы, не входящих в данное уравнение, не равен нулю и количество эндогенных переменных системы без единицы равно рангу этой матрицы, то уравнение модели идентифицируемо.
Слайд 27Если выполнимо условие:
n < p+1, то уравнение сверхидентифицируемо;
n > p+1,
то уравнение неидентифицируемо.
Проверка структурной модели на идентифицируемость позволяет установить степень
возможности оценки коэффициентов структурных уравнений по коэффициентам приведенных уравнений.
Слайд 28Пример: проверить идентифицированы ли уравнения (1) и (2) модели 2
предложения и спроса кейнсианского типа
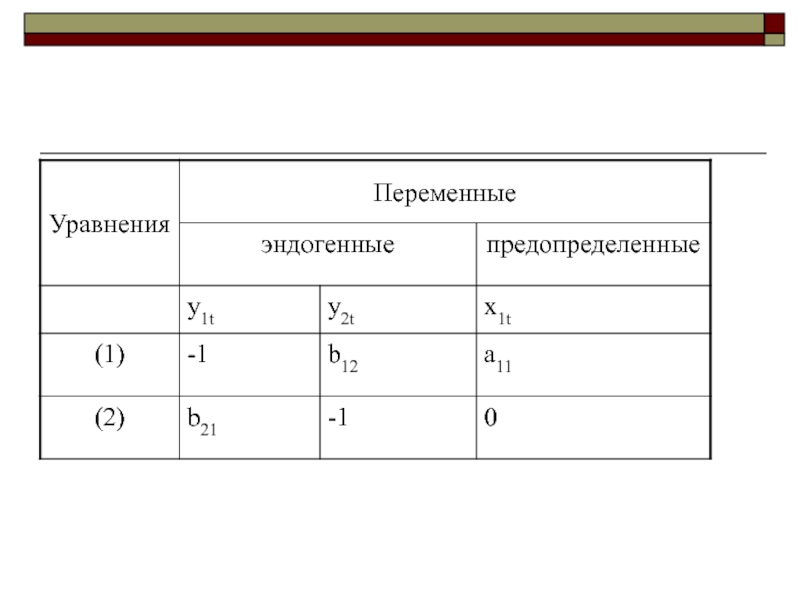
Слайд 29Уравнение (1):
n=2, p=1. Выполняется необходимое условие идентификации: 2=1+1.
A* - матрица
коэффициентов при переменных системы, не входящих в уравнение.
Rang =
2 (ранг равен количеству эндогенных переменных модели минус один).
|A*|= – a23 ≠ 0 . Достаточное условие идентифицируемости также выполняется.
Уравнение (1) идентифицируемое.
Слайд 30Уравнение (2):
n=2, p=1. Выполняется необходимое условие идентификации: 2=1+1.
A* - матрица
коэффициентов при переменных системы, не входящих в уравнение.
Rang =
2 (ранг равен количеству эндогенных переменных модели минус один).
|A*|= – a11 ≠ 0 . Достаточное условие идентифицируемости также выполняется.
Уравнение (2) идентифицируемое.
Слайд 31Т.о., система одновременных уравнений идентифицируемая в силу идентифицируемости уравнений (1)
и (2).
Для оценки параметров системы можно применять как косвенный МНК,
так и двухшаговый МНК.
Слайд 32Приведенная форма модели имеет вид:
Применив соответствующие статистические данные, можно с
помощью косвенного МНК найти несмещенные и состоятельные оценки структурной формы,
тем самым смоделировав реальную экономическую ситуацию изучения спроса-предложения с учетом дохода в текущий период и цены товара в предыдущий период.
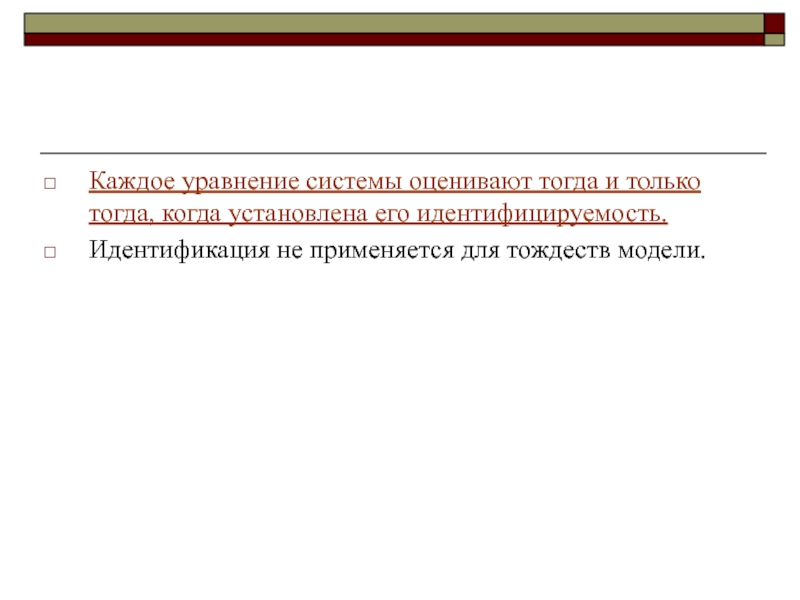
Слайд 33Каждое уравнение системы оценивают тогда и только тогда, когда установлена
его идентифицируемость.
Идентификация не применяется для тождеств модели.
Слайд 34Модель 3. Предложение денег и спрос на деньги
Слайд 36Уравнение (2):
n=2, p=0, n > p+1.
Уравнение неидентифицируемое, следовательно, не
идентифицируема
вся система.
В этом случае изменяют модель так, чтобы она,
с
одной стороны, содержала основные эндогенные и экзогенные переменные, которые определяют спрос и предложение на деньги,
с другой – была эконометрически разрешима.
Слайд 37Методы решения систем одновременных уравнений
Косвенный метод наименьших квадратов (КМНК)
Двухшаговый метод
наименьших квадратов (ДМНК)
Трехшаговый метод наименьших квадратов (ТМНК)
Метод максимального правдоподобия с
полной информацией (ММПf)
Метод максимального правдоподобия при ограниченной информации (ММПs)
Слайд 38Косвенный метод наименьших квадратов
Косвенный МНК основан на получении состоятельных и
несмещенных оценок параметров структурной формы модели по оценкам параметров приведенной
формы.
Последние являются состоятельными и несмещенными в силу применения к каждому уравнению приведенной формы МНК.
Слайд 39Алгоритм применения косвенного метода наименьших квадратов
Оценить параметры системы одновременных уравнений,
которая задана структурной формой модели.
Структурная форма модели преобразуется в приведенную
форму.
С помощью МНК оцениваются параметры приведенной формы.
Приведенная форма преобразуется в структурную форму.
Несмещенные и состоятельные оценки параметров структурной формы получены.
Слайд 40Пример: Оценить параметры идентифицируемой системы одновременных уравнений, которая задана структурной
формой модели.
Слайд 41Область применения косвенного МНК ограничивается идентифицируемыми системами одновременных уравнения.
Важно
Слайд 42Двухшаговый метод наименьших квадратов
Двухшаговый МНК применяется как для идентифицируемых, так
и сверхидентифицируемых систем одновременных уравнений.
В этом смысле метод является общим
по отношению к косвенному МНК.
Слайд 43Алгоритм применения двухшагового метода наименьших квадратов
Оценить параметры сверхидентифицируемой системы одновременных
уравнений, которая задана структурной формой модели.
Структурная форма модели преобразуется в
приведенную форму.
С помощью МНК оцениваются параметры приведенной формы.
В правой части сверхидентифицируемого уравнения структурной модели выбираются эндогенные переменные и рассчитываются их теоретические значения по соответствующим приведенным уравнениям.
С помощью МНК на основе фактических значений предопределенных и теоретических значений эндогенных переменных оцениваются параметры сверхидентифицируемого уравнения структурной модели.
Несмещенные и состоятельные оценки параметров структурной формы получены.
Слайд 44Пример: Оценить параметры сверхидентифицируемой системы одновременных уравнений, которая задана структурной
формой модели.
Слайд 45Двухшаговый МНК обладает свойствами, благодаря которым его практическая эффективность остается
достаточно высокой.
Для двухшагового МНК достаточно оперировать экзогенными и предопределенными переменными
модели.
Эффективность двухшагового МНК определяется высоким коэффициентом детерминации R2 приведенных уравнений модели. В том случае, когда R2 низкий, расчетные значения эндогенной переменной слабо аппроксимируют ее фактические значения.