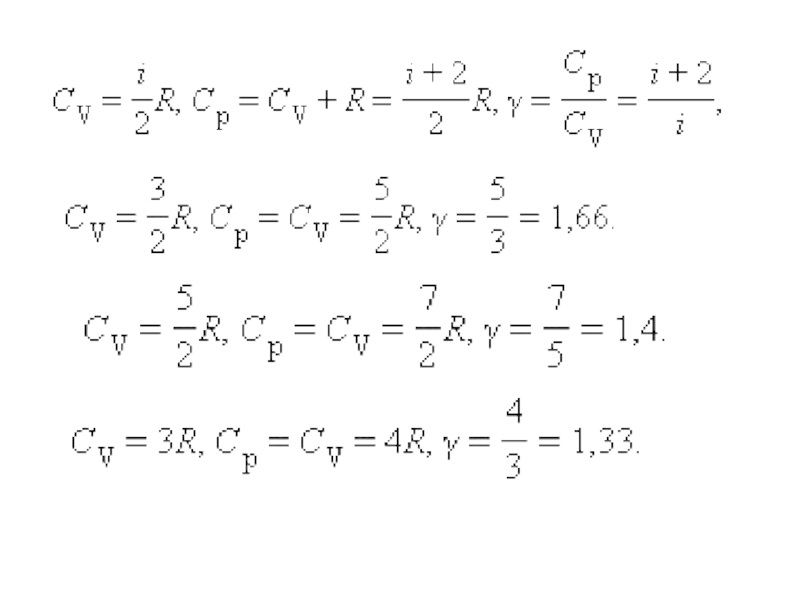Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
слайды к лекционному материалу ФИЗИКА 1 часть
Содержание
- 1. слайды к лекционному материалу ФИЗИКА 1 часть
- 2. ОСНОВНЫЕ РАЗДЕЛЫ ОБЩЕЙ ФИЗИКИмеханика термодинамика и молекулярная физикаэлектричество и магнетизмоптикаатомная физикаквантовая физикаядерная физика
- 3. МЕХАНИКА раздел физики, изучающий простейшую форму движения
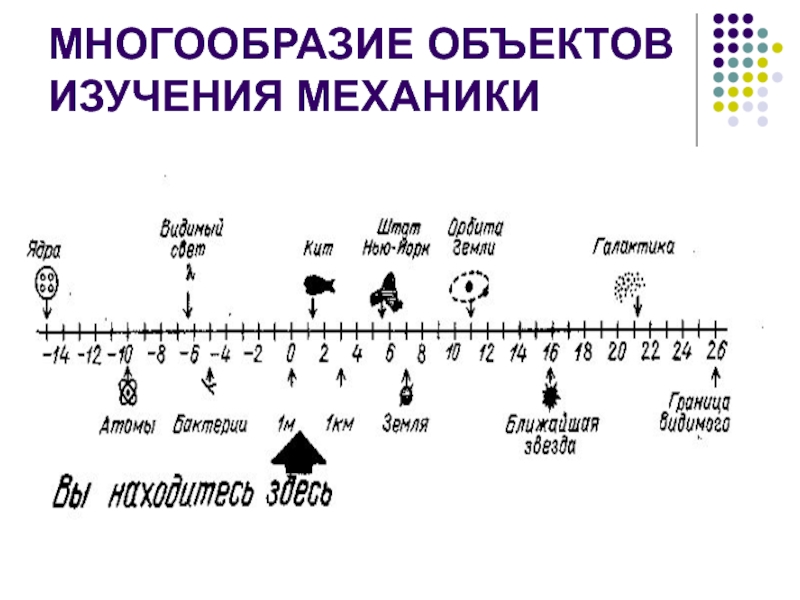
- 4. МНОГООБРАЗИЕ ОБЪЕКТОВ ИЗУЧЕНИЯ МЕХАНИКИ
- 5. ДЕЛЕНИЯ МЕХАНИКИклассическая (ньютонова) механика- квантовая механика- релятивистская механика
- 6. РАЗДЕЛЫ КЛАССИЧЕСКОЙ МЕХАНИКИСТАТИКА (изучает условия равновесия тел)
- 7. ОСНОВНЫЕ ЗАДАЧИ КЛАССИЧЕСКОЙ (НЬЮТОНОВОЙ) МЕХАНИКИизучение всевозможных движений
- 8. ОСНОВНЫЕ МОДЕЛИ МЕХАНИКИматериальная точка (тело, форма и
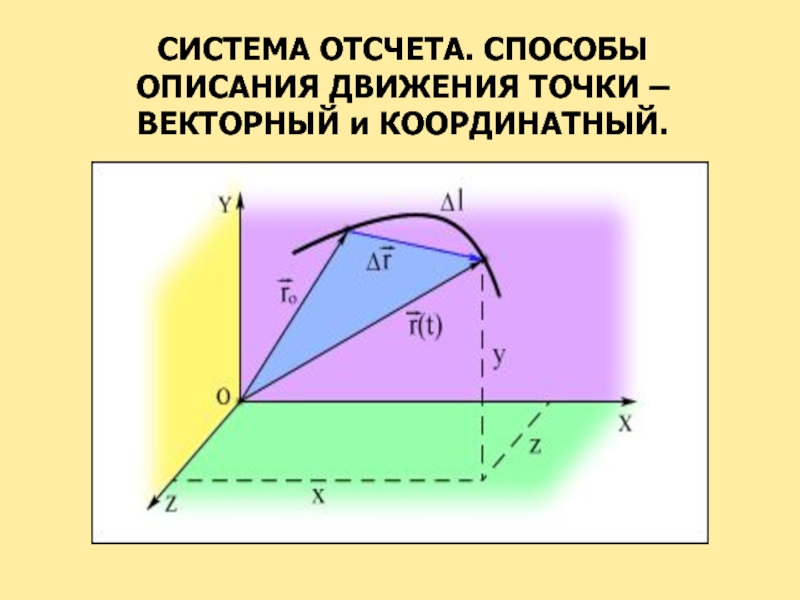
- 9. СИСТЕМА ОТСЧЕТА. СПОСОБЫ ОПИСАНИЯ ДВИЖЕНИЯ ТОЧКИ – ВЕКТОРНЫЙ и КООРДИНАТНЫЙ.
- 10. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ ВЕЛИЧИНЫперемещениемгновенная скоростьмгновенное ускорение
- 11. СКАЛЯРЫ И ВЕКТОРЫ. КООРДИНАТНОЕ РАЗЛОЖЕНИЕ КИНЕМАТИЧЕСКИХ ВЕЛИЧИНкоординатаскорость
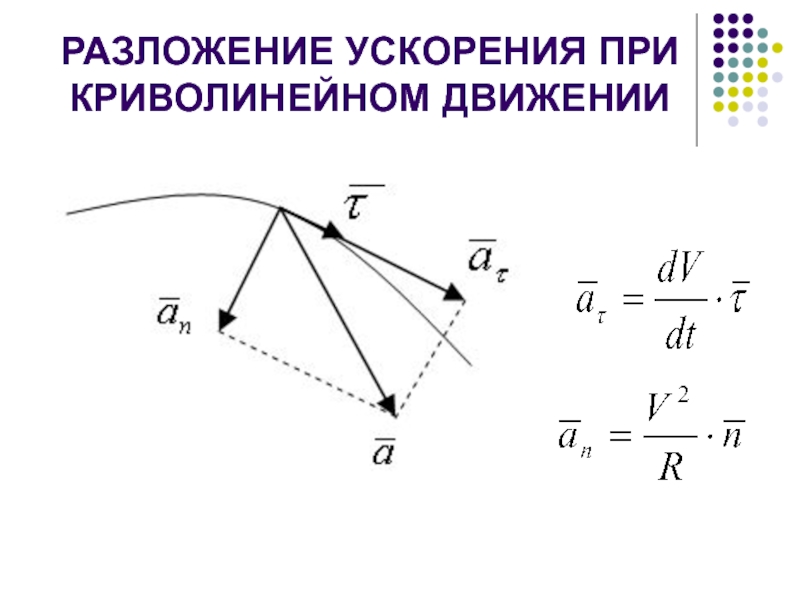
- 12. РАЗЛОЖЕНИЕ УСКОРЕНИЯ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
- 13. ХАРАКТЕРИСТИКА ПРОСТЕЙШИХ ВИДОВ ДВИЖЕНИЯПрямолинейное равномерноеПрямолинейное равноускоренноеПрямолинейное равнозамедленноеРавномерное движение по окружности
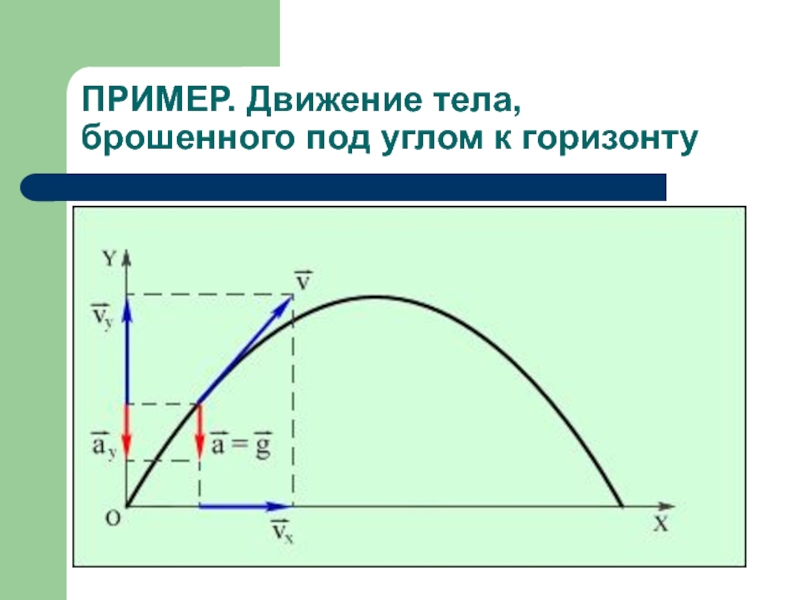
- 14. ПРИМЕР. Движение тела, брошенного под углом к горизонту
- 15. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ Движение тел можно описывать
- 16. ПРИНЦИПЫ КИНЕМАТИКИ ТВЕРДОГО ТЕЛАПоступательное движение твердого тела
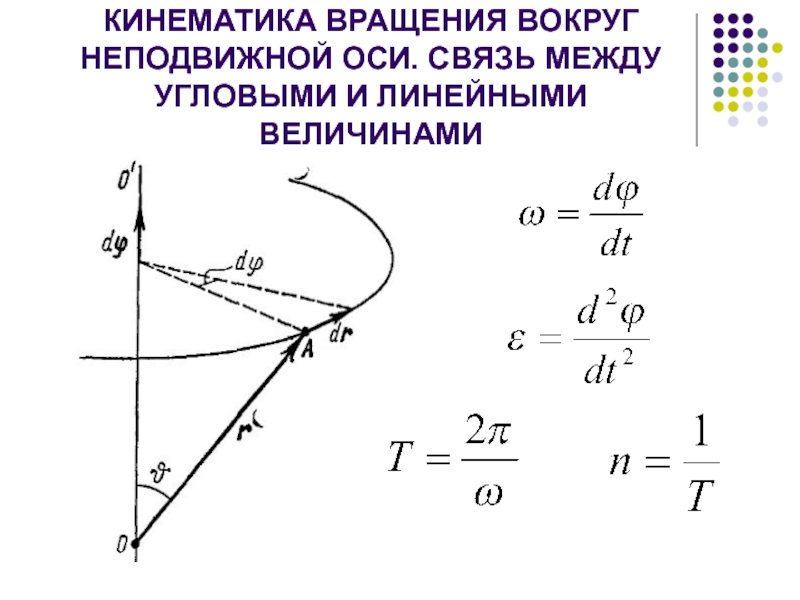
- 17. КИНЕМАТИКА ВРАЩЕНИЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ. СВЯЗЬ МЕЖДУ УГЛОВЫМИ И ЛИНЕЙНЫМИ ВЕЛИЧИНАМИ
- 18. ОСНОВНЫЕ ПОНЯТИЯ ДИНАМИКИМАССА материальной точки – положительная
- 19. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ И ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯВсе механические явления протекают одинаково во всех инерциальных системах отсчетаx = x' + υt, y = y', z = z', t = t'
- 20. НЬЮТОН, ИСААК (Newton, Isaac) (1642–1727), английский математик
- 21. КЛАССИЧЕСКАЯ МЕХАНИКА НЬЮТОНА I ЗАКОН –
- 22. КЛАССИЧЕСКАЯ МЕХАНИКА НЬЮТОНА II ЗАКОН –
- 23. КЛАССИЧЕСКАЯ МЕХАНИКА НЬЮТОНА III ЗАКОН –
- 24. ПРИНЦИП ДЕТЕРМИНИЗМА П.ЛАПЛАСАДЕТЕРМИНИЗМ (от англ. determine -
- 25. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСАИмпульс
- 26. Иллюстрация закона сохранения импульса
- 27. РАБОТА И МЕХАНИЧЕСКАЯ ЭНЕРГИЯ Энергией называется скалярная
- 28. ВИДЫ (ФОРМЫ) ЭНЕРГИИ– механическая;– внутренняя;– электромагнитная;– ядерная и т.д.
- 29. КИНЕТИЧЕСКАЯ ЭНЕРГИЯФизическая величина, равная половине произведения массы
- 30. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯэто часть энергии механической системы, зависящая
- 31. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ
- 32. МЕХАНИЧЕСКАЯ РАБОТАРаботой силы F на бесконечно малом перемещении ds называется скалярная величинав случае конечного перемещения:
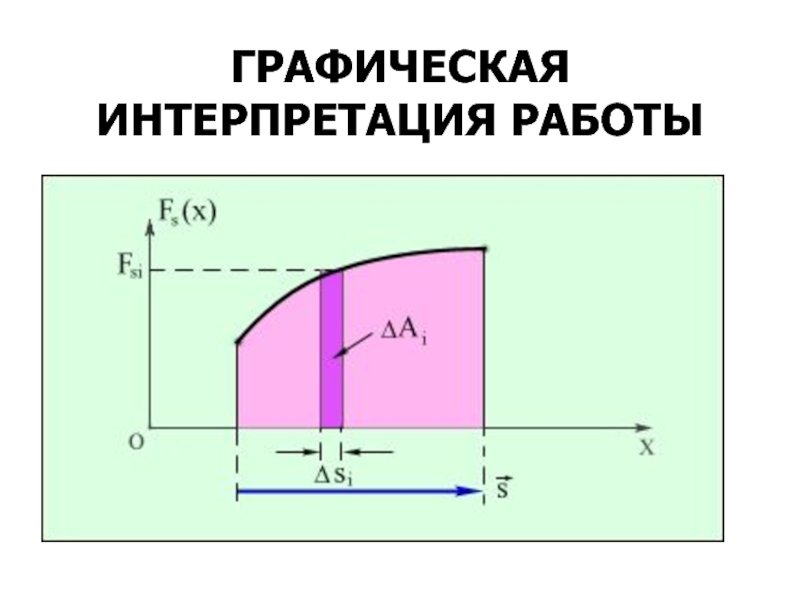
- 33. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ РАБОТЫ
- 34. ОСОБЕННОСТИ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯМомент силы относительно неподвижной точки Главный момент системы сил
- 35. ОСОБЕННОСТИ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯМомент импульса материальной точки относительно неподвижной точки Момент импульса системы точек
- 36. ОСОБЕННОСТИ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯМомент инерции материальной точки относительно неподвижной оси Момент импульса системы материальных точек
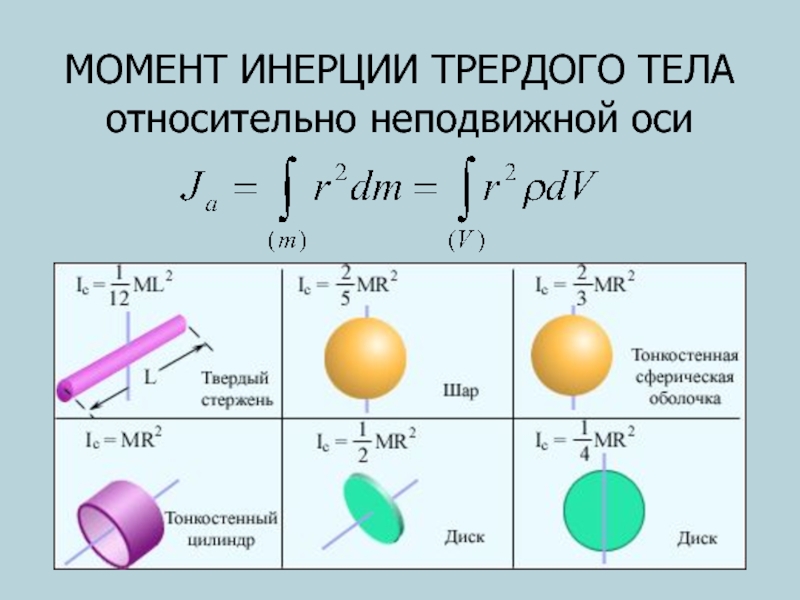
- 37. МОМЕНТ ИНЕРЦИИ ТРЕРДОГО ТЕЛА относительно неподвижной оси
- 38. ТЕОРЕМА ГЮЙГЕНСА-ШТЕЙНЕРАМомент инерции тела относительно какой либо
- 39. СООТНОШЕНИЕ ДИНАМИЧЕСКИХ ВЕЛИЧИН
- 40. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСАдля точки (системы точек) для абсолютно твердого тела
- 41. Иллюстрация закона сохранения момента импульса
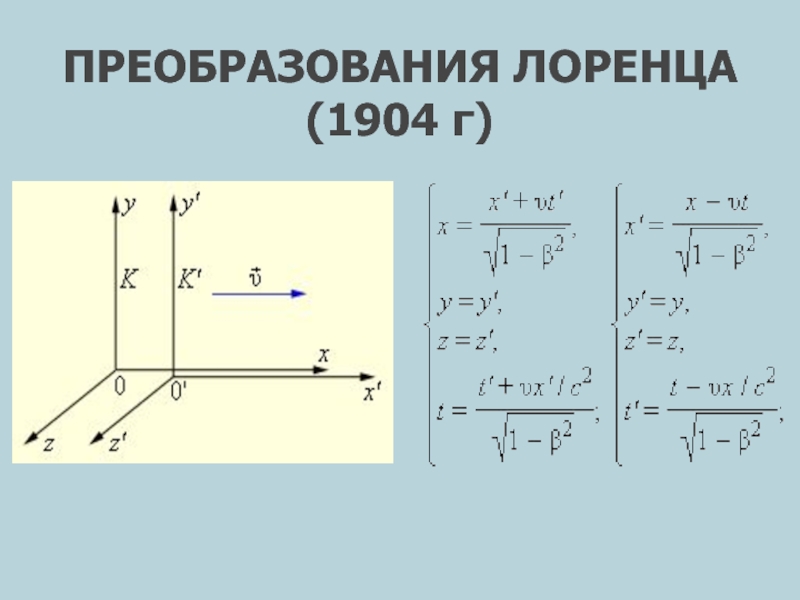
- 42. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА (1904 г)
- 43. СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА- РЕЛЯТИВИСТСКОЕ ЗАМЕДЛЕНИЕ ВРЕМЕНИ- РЕЛЯТИВИСТСКОЕ СОКРАЩЕНИЕ ДЛИНЫ
- 44. Слайд 44
- 45. ЗАКОН ВЗАИМОСВЯЗИ МАССЫ И ЭНЕРГИИМАССА тела характеризует
- 46. ТЕРМОДИНАМИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА
- 47. ДВА ПОДХОДА К ИССЛЕДОВАНИЮ ТЕПЛОВЫХ ЯВЛЕНИЙ
- 48. ДВА ПОДХОДА К ИССЛЕДОВАНИЮ ТЕПЛОВЫХ ЯВЛЕНИЙ
- 49. ОПИСАНИЕ ТЕРМОДИНАМИЧЕСКИХ СИСТЕМтермодинамические системы – макроскопические объекты
- 50. РАВНОВЕСИЕ и ПРОЦЕССТермодинамическое равновесие характеризуется постоянством всех
- 51. ИДЕАЛЬНЫЙ ГАЗидеальный газ – это газ, взаимодействие
- 52. ИЗОПРОЦЕССЫ- это процессы, при протекании которых сохраняется
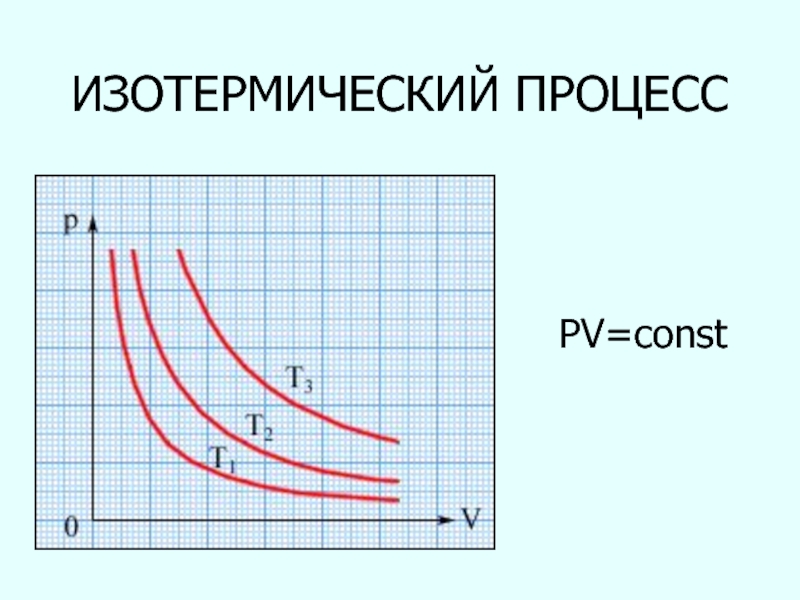
- 53. ИЗОТЕРМИЧЕСКИЙ ПРОЦЕССPV=const
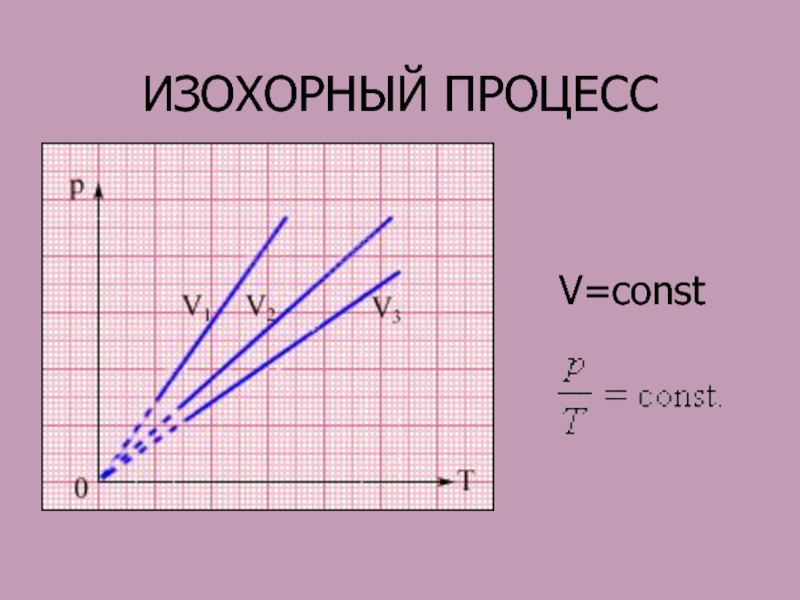
- 54. ИЗОХОРНЫЙ ПРОЦЕССV=const
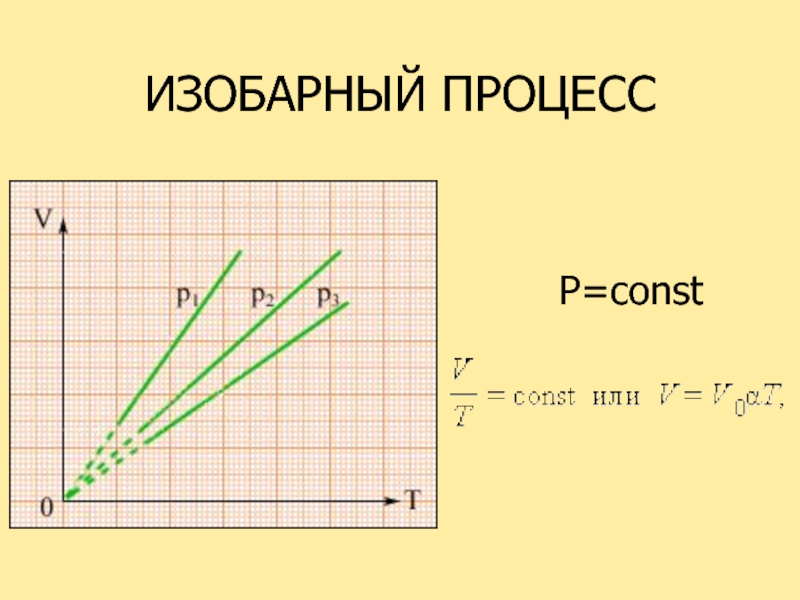
- 55. ИЗОБАРНЫЙ ПРОЦЕССP=const
- 56. БРОУНОВСКОЕ ДВИЖЕНИЕ (1827)
- 57. БАЗОВЫЕ ПОЛОЖЕНИЯ МКТВсе вещества – жидкие, твердые
- 58. ВНУТРЕННЯЯ ЭНЕРГИЯвсе макроскопические тела обладают энергией, заключенной
- 59. ВНУТРЕННЯЯ ЭНЕРГИЯявляется однозначной функций состояния термодинамической системыU
- 60. КОЛИЧЕСТВО ТЕПЛОТЫ И РАБОТАКоличеством теплоты Q, полученной
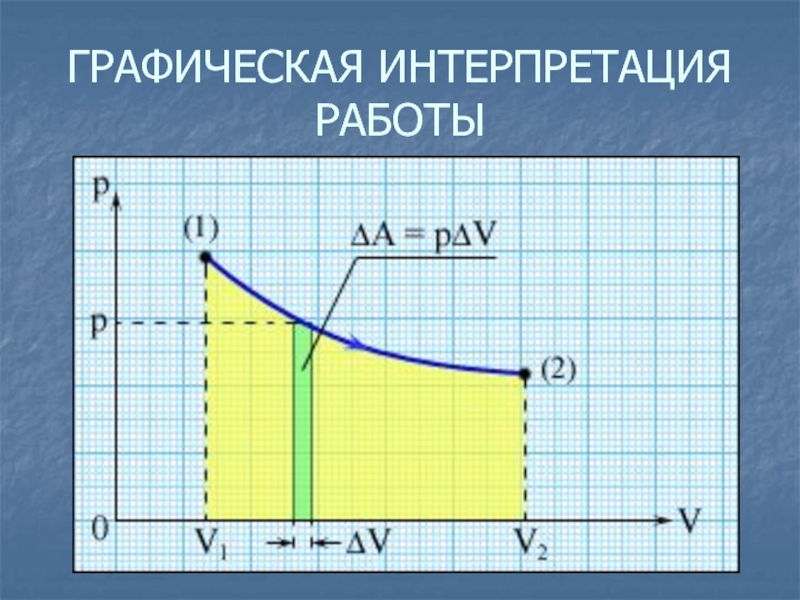
- 61. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ РАБОТЫ
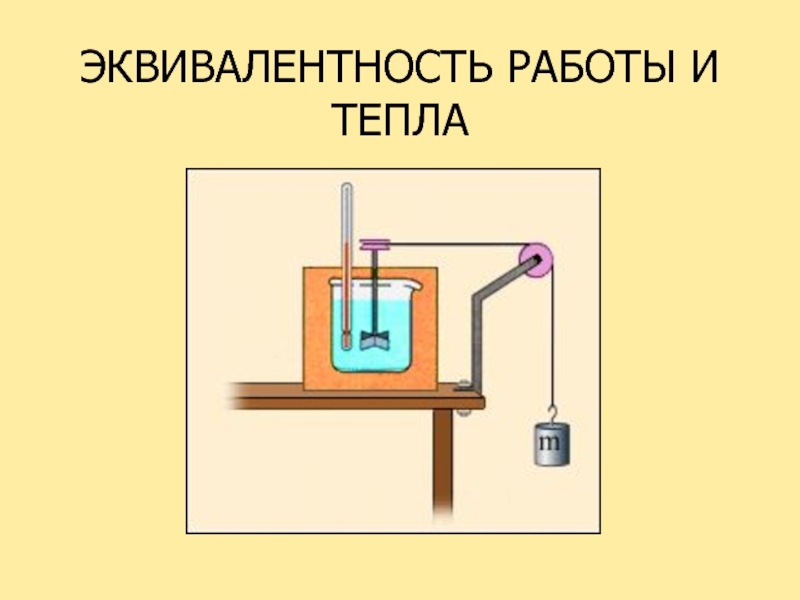
- 62. ЭКВИВАЛЕНТНОСТЬ РАБОТЫ И ТЕПЛА
- 63. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ Количество теплоты, полученное системой, идет
- 64. ТЕПЛОЕМКОСТЬЕсли в результате теплообмена телу передается некоторое
- 65. ВИДЫ ТЕПЛОЕМКОСТИУдельная теплоемкость относится к массе вещества
- 66. КЛАССИЧЕСКАЯ ТЕОРИЯ ТЕПЛОЕМКОСТИ (Л. Больцман)Теорема о равномерном
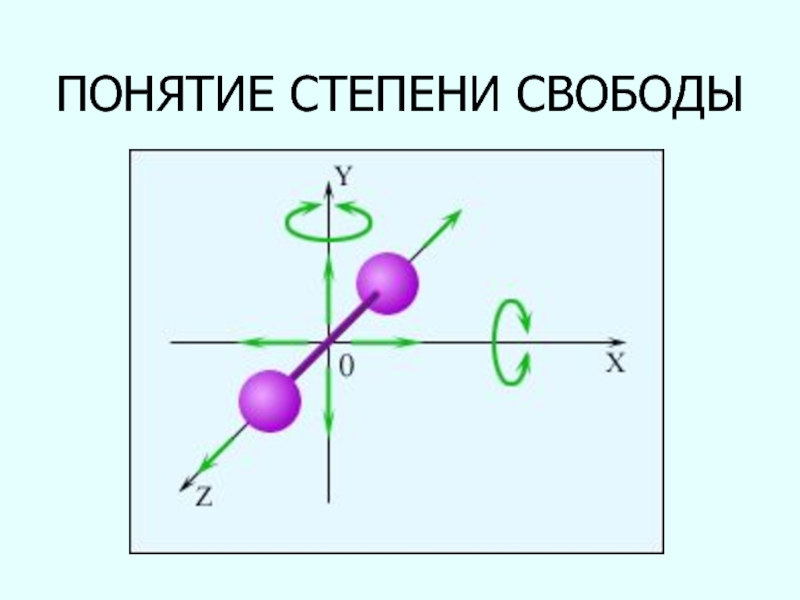
- 67. ПОНЯТИЕ СТЕПЕНИ СВОБОДЫ
- 68. Слайд 68
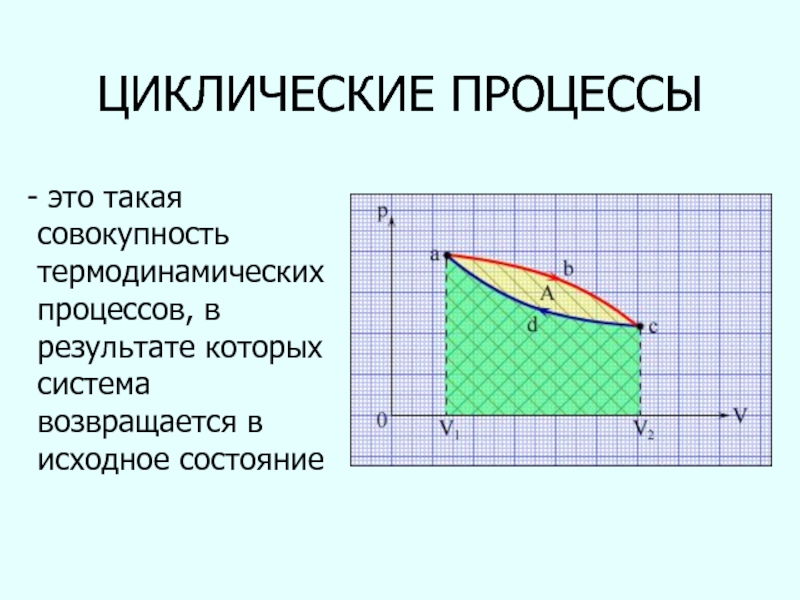
- 69. ЦИКЛИЧЕСКИЕ ПРОЦЕССЫ - это такая совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние
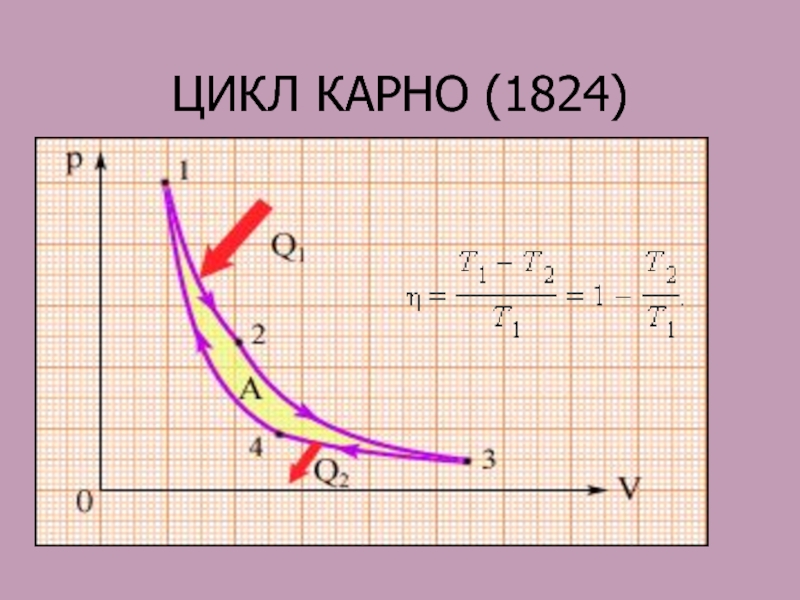
- 70. ЦИКЛ КАРНО (1824)
- 71. ОБРАТИМЫЕ ПРОЦЕССЫОбратимыми процессами называют процессы перехода системы
- 72. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИНевозможен процесс, единственным результатом которого
- 73. ЭНТРОПИЯэто функция состояния термодинамической системы, изменение которой
- 74. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ (закон неубывания энтропии)При любых
- 75. ЭЛЕКТРОДИНАМИКАЭлектрический заряд – это физическая величина, характеризующая
- 76. Слайд 76
- 77. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДАв изолированной системе алгебраическая сумма зарядов всех тел остается постоянной
- 78. ЗАКОН КУЛОНАСилы взаимодействия неподвижных зарядов прямо пропорциональны
- 79. ЭЛЕКТРИЧЕСКОЕ ПОЛЕкаждое заряженное тело создает в окружающем
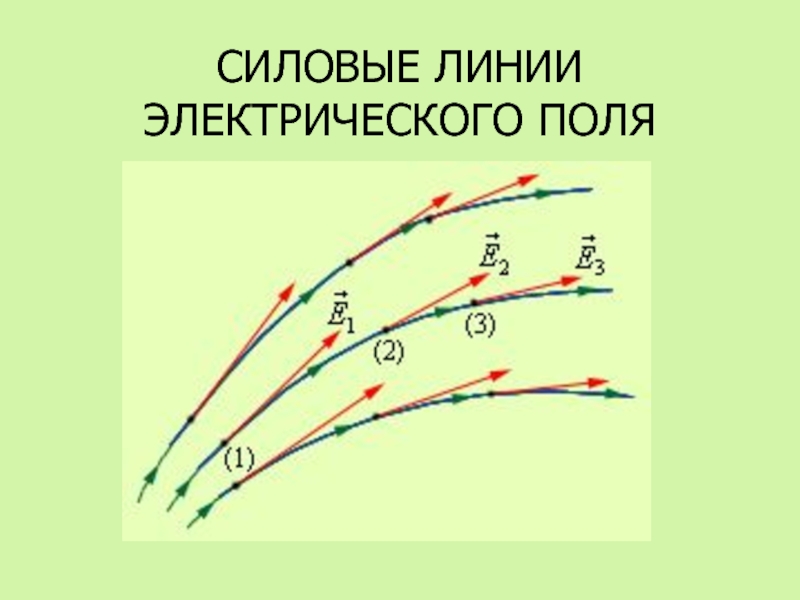
- 80. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
- 81. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ
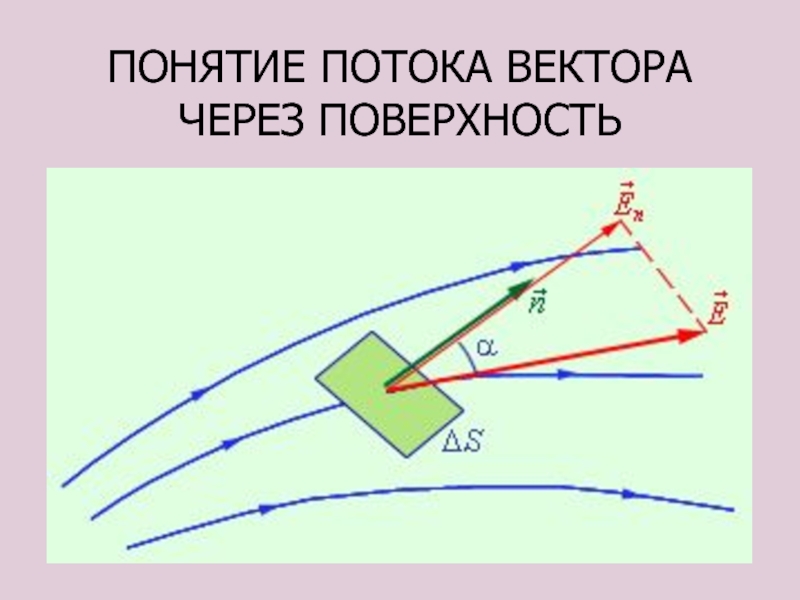
- 82. ПОНЯТИЕ ПОТОКА ВЕКТОРА ЧЕРЕЗ ПОВЕРХНОСТЬ
- 83. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССАПоток вектора напряженности электростатического поля
- 84. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯравен работе, которую совершают электрические
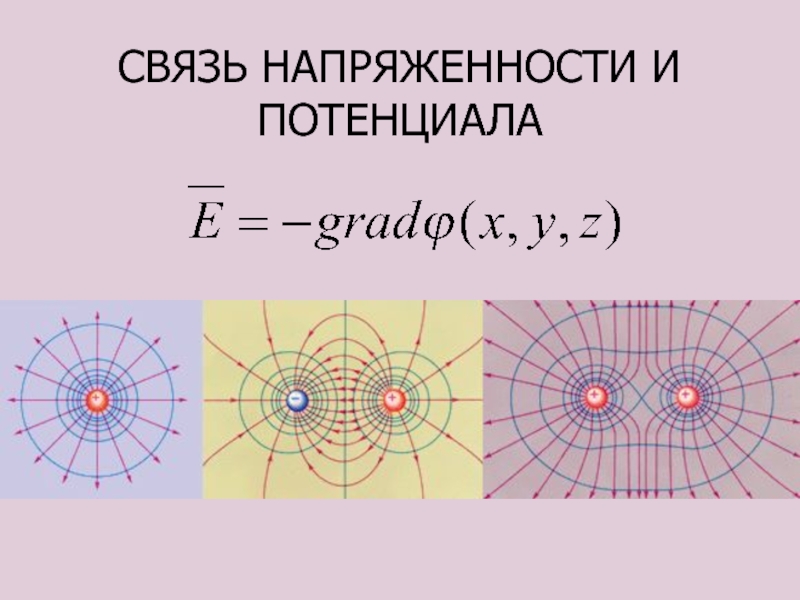
- 85. СВЯЗЬ НАПРЯЖЕННОСТИ И ПОТЕНЦИАЛА
- 86. ПОТЕНЦИАЛПотенциал точечного зарядаПринцип суперпозиции потенциалов
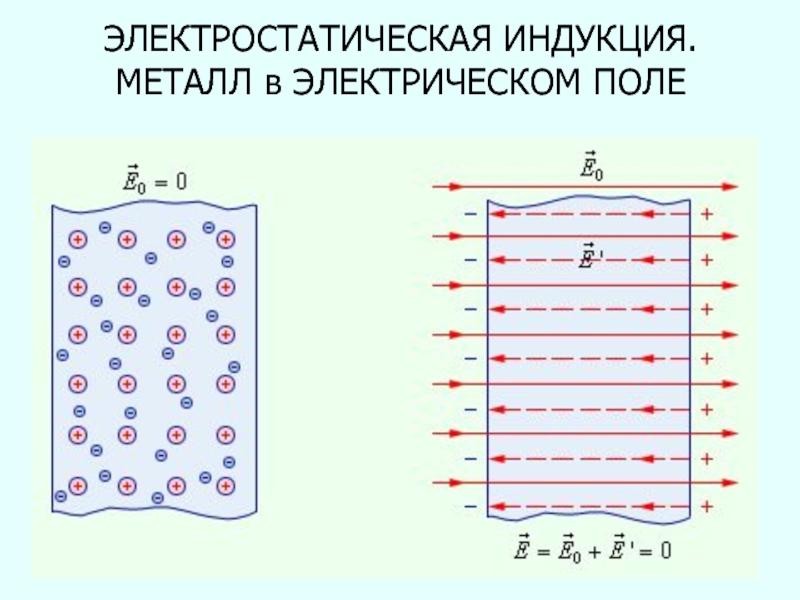
- 87. ЭЛЕКТРОСТАТИЧЕСКАЯ ИНДУКЦИЯ. МЕТАЛЛ в ЭЛЕКТРИЧЕСКОМ ПОЛЕ
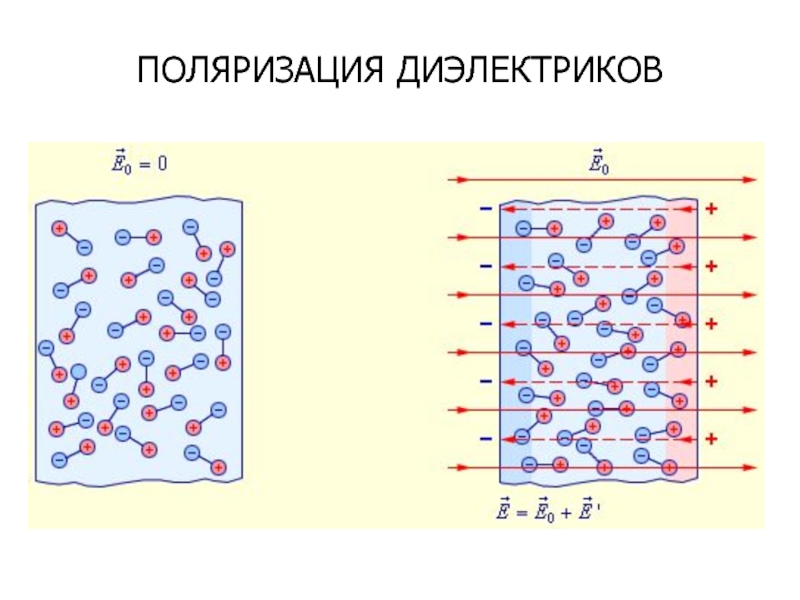
- 88. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
- 89. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ физическая величина, равная отношению
- 90. НАПРЯЖЕННОСТЬ И ПОТЕНЦИАЛ ТОЧЕЧНОГО ЗАРЯДА В ДИЭЛЕКТРИКЕ
- 91. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ Электроемкостью системы из двух
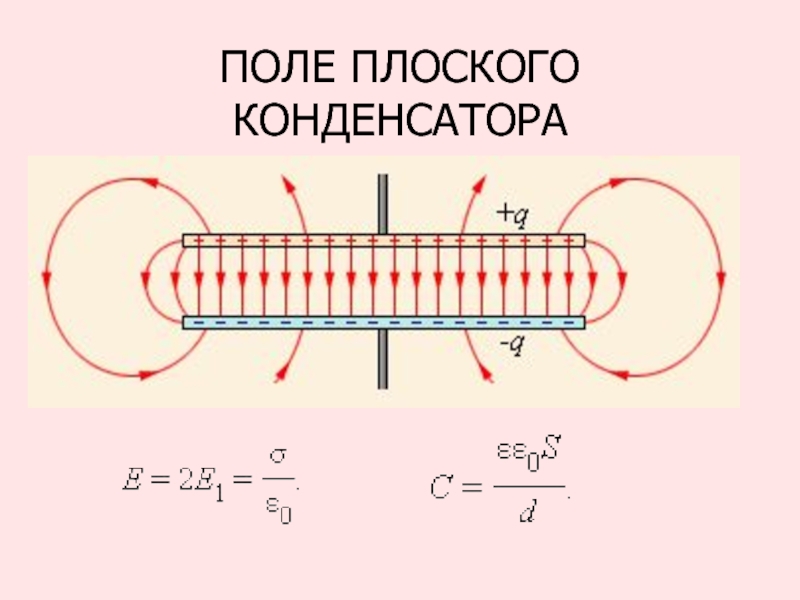
- 92. ПОЛЕ ПЛОСКОГО КОНДЕНСАТОРА
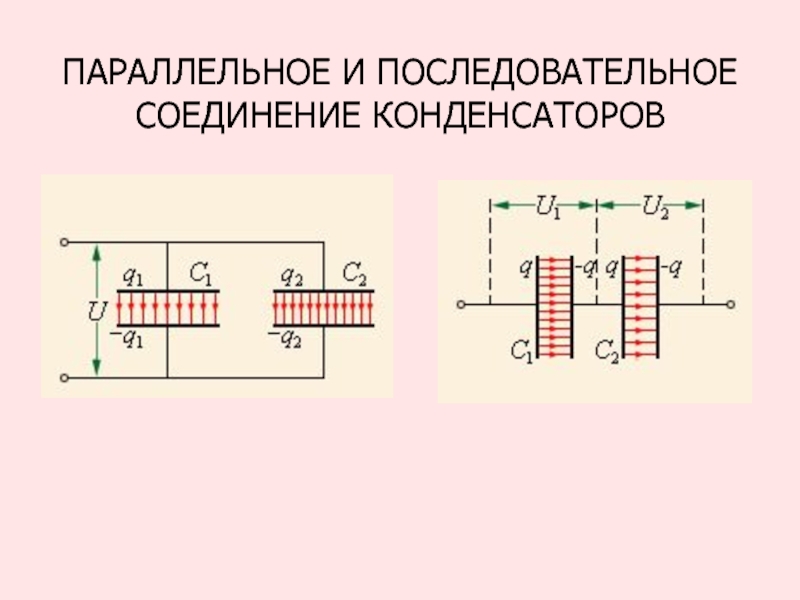
- 93. ПАРАЛЛЕЛЬНОЕ И ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ КОНДЕНСАТОРОВ
- 94. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯэнергия поля конденсатораэнергия электрического поляобъемная плотность энергии поля
- 95. ЭЛЕКТРИЧЕСКИЙ ТОК упорядоченное движение электронов в металлическом проводнике и ток
- 96. ЗАКОН ОМА (для участка цепи) сила
- 97. ЭЛЕКТРОДВИЖУЩАЯ СИЛА физическая величина, равная отношению
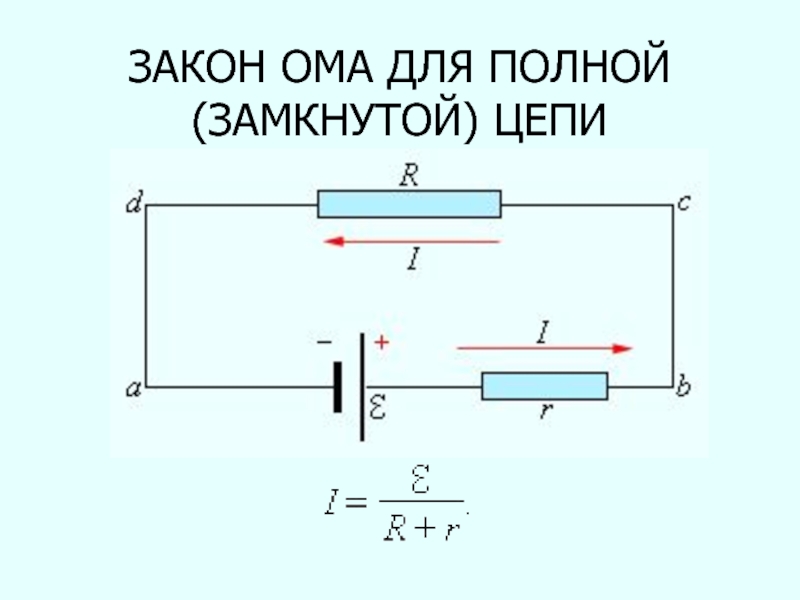
- 98. ЗАКОН ОМА ДЛЯ ПОЛНОЙ (ЗАМКНУТОЙ) ЦЕПИ
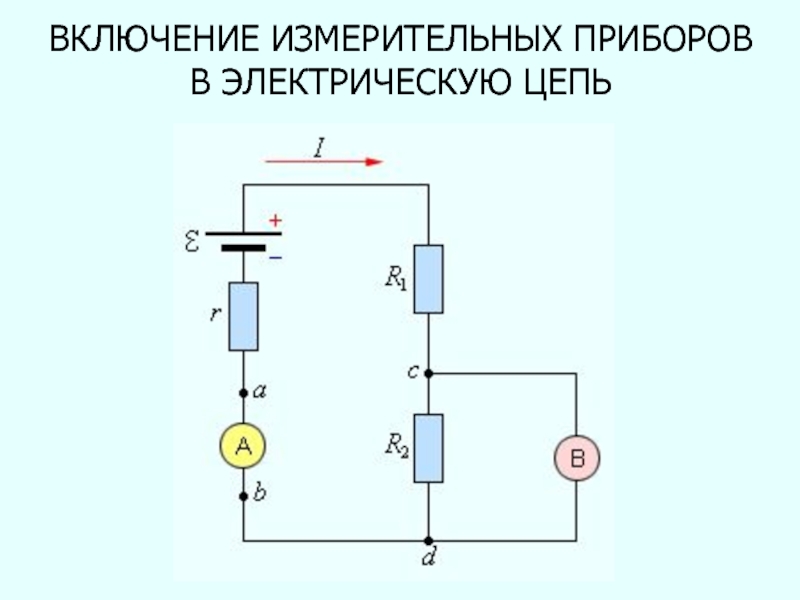
- 99. ВКЛЮЧЕНИЕ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ В ЭЛЕКТРИЧЕСКУЮ ЦЕПЬ
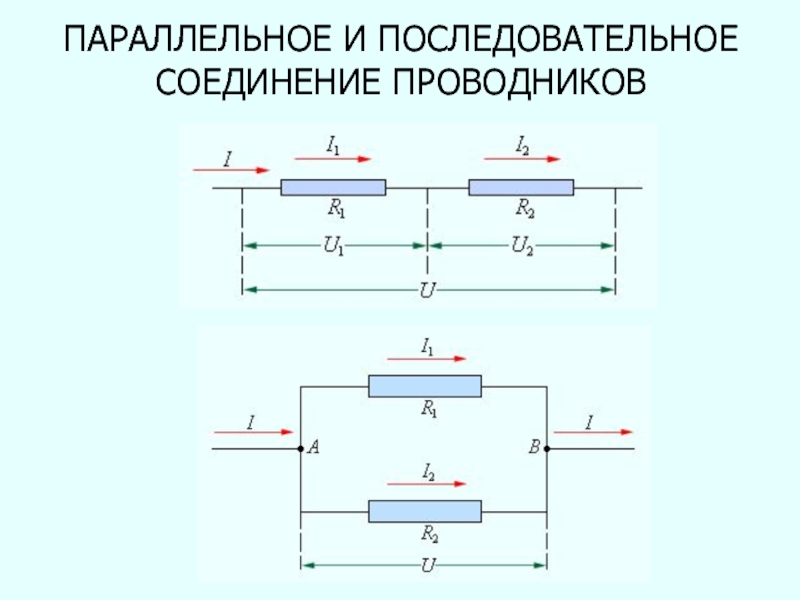
- 100. ПАРАЛЛЕЛЬНОЕ И ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ
- 101. ПРАВИЛА КИРХГОФА1 правило: алгебраическая сумма сил токов
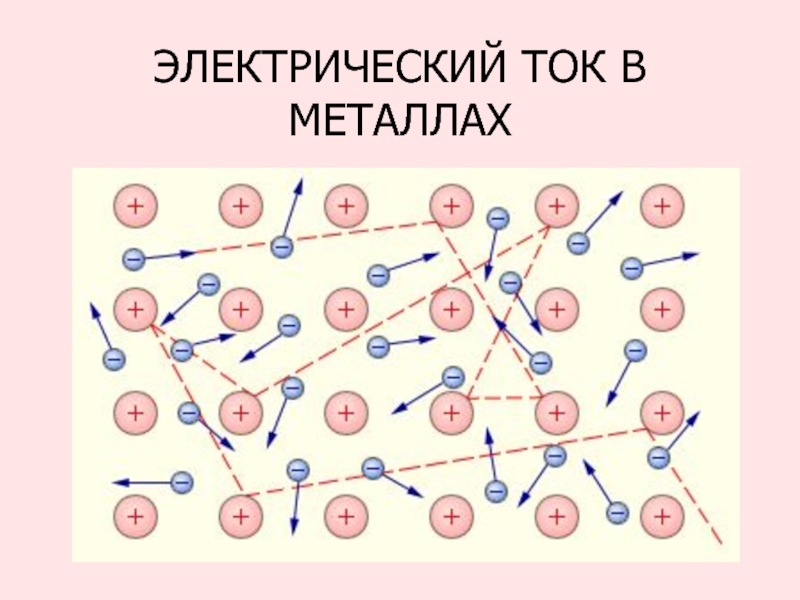
- 102. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ
- 103. Скачать презентанцию
ОСНОВНЫЕ РАЗДЕЛЫ ОБЩЕЙ ФИЗИКИмеханика термодинамика и молекулярная физикаэлектричество и магнетизмоптикаатомная физикаквантовая физикаядерная физика
Слайды и текст этой презентации
Слайд 2ОСНОВНЫЕ РАЗДЕЛЫ ОБЩЕЙ ФИЗИКИ
механика
термодинамика и молекулярная физика
электричество и магнетизм
оптика
атомная
физика
Слайд 3МЕХАНИКА
раздел физики, изучающий простейшую форму движения – механическое движение,
связанное с перемещением тела в пространстве и времени
Слайд 5ДЕЛЕНИЯ МЕХАНИКИ
классическая (ньютонова) механика
- квантовая механика
- релятивистская механика
Слайд 6РАЗДЕЛЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
СТАТИКА (изучает условия равновесия тел)
КИНЕМАТИКА (изучает способы
описания движений независимо от причин возникновения движений)
ДИНАМИКА (изучает движение тел
в связи с причинами возникновения движений)
Слайд 7ОСНОВНЫЕ ЗАДАЧИ КЛАССИЧЕСКОЙ (НЬЮТОНОВОЙ) МЕХАНИКИ
изучение всевозможных движений и обобщение полученных
результатов в виде законов
отыскание общих свойств, присущих любой системе
независимо от рода взаимодействий в системе
Слайд 8ОСНОВНЫЕ МОДЕЛИ МЕХАНИКИ
материальная точка (тело, форма и размер которого несущественны
в условиях данной задачи
абсолютно твердое тело (протяженное тело, расстояние между
двумя любыми точками которого всегда постоянно)
Слайд 13ХАРАКТЕРИСТИКА ПРОСТЕЙШИХ ВИДОВ ДВИЖЕНИЯ
Прямолинейное равномерное
Прямолинейное равноускоренное
Прямолинейное равнозамедленное
Равномерное движение по окружности
Слайд 15ПРИНЦИП ОТНОСИТЕЛЬНОСТИ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ
Движение тел можно описывать в различных системах
отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако
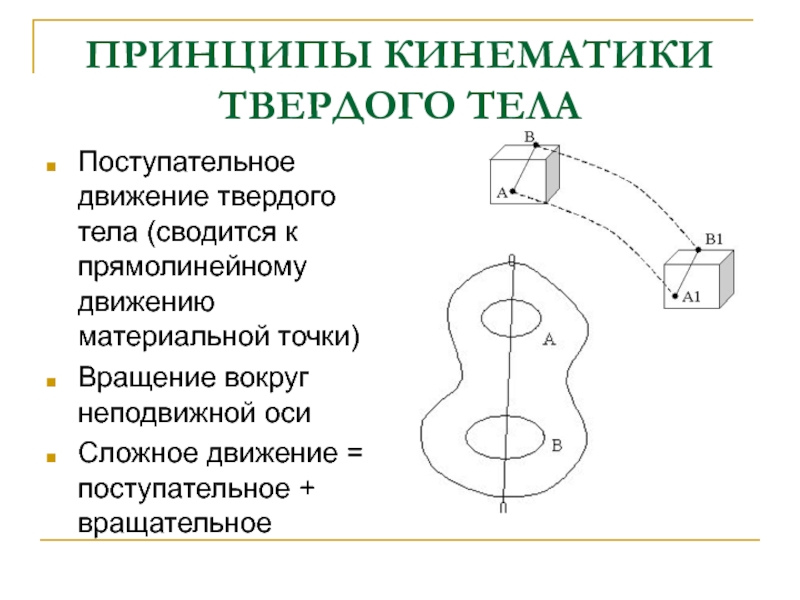
кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными.
Слайд 16ПРИНЦИПЫ КИНЕМАТИКИ ТВЕРДОГО ТЕЛА
Поступательное движение твердого тела (сводится к прямолинейному
движению материальной точки)
Вращение вокруг неподвижной оси
Сложное движение = поступательное +
вращательное
Слайд 18ОСНОВНЫЕ ПОНЯТИЯ ДИНАМИКИ
МАССА материальной точки – положительная скалярная величина, являющаяся
мерой инертности точки
СИЛА – причина механического движения, мера действия на
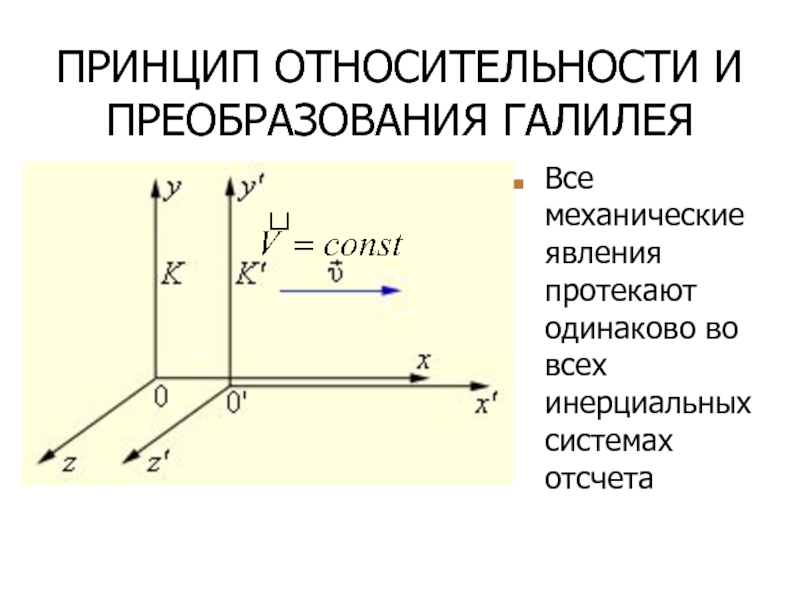
рассматриваемое тело со стороны других тел
Слайд 19ПРИНЦИП ОТНОСИТЕЛЬНОСТИ И ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯ
Все механические явления протекают одинаково во
всех инерциальных системах отсчета
x = x' + υt, y = y', z = z', t = t'
Слайд 20НЬЮТОН, ИСААК (Newton, Isaac) (1642–1727), английский математик и естествоиспытатель, механик,
астроном и физик, основатель классической физики
Слайд 21КЛАССИЧЕСКАЯ МЕХАНИКА НЬЮТОНА
I ЗАКОН – ЗАКОН ИНЕРЦИИ
Существуют такие системы
отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость
неизменной по модулю и направлению.Инерция - свойство тела сохранять свою скорость при отсутствии действия на него других тел
Слайд 22КЛАССИЧЕСКАЯ МЕХАНИКА НЬЮТОНА
II ЗАКОН – ОСНОВНОЙ ЗАКОН ДИНАМИКИ
где
- ускорение материальной точки
-
величина постоянной силы, действующей на точку
- масса материальной точки
Слайд 23КЛАССИЧЕСКАЯ МЕХАНИКА НЬЮТОНА
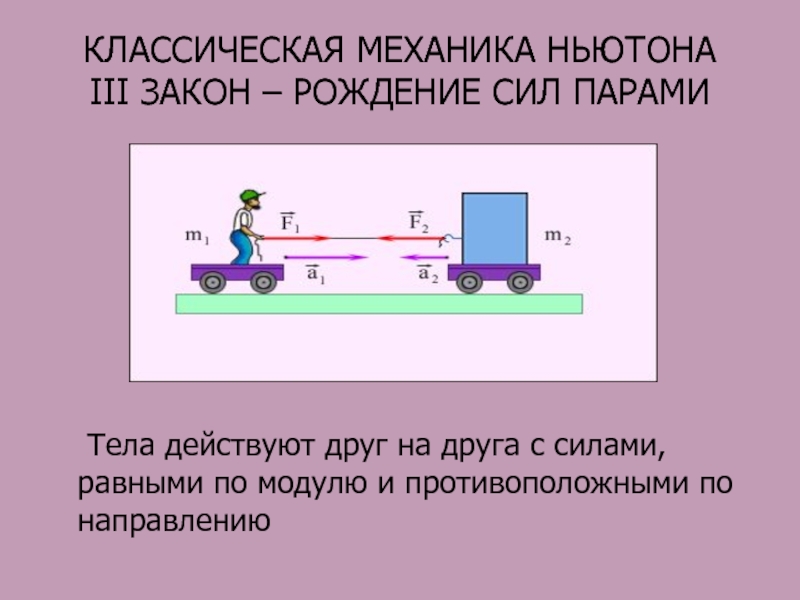
III ЗАКОН – РОЖДЕНИЕ СИЛ ПАРАМИ
Тела действуют
друг на друга с силами, равными по модулю и противоположными
по направлению
Слайд 24ПРИНЦИП ДЕТЕРМИНИЗМА П.ЛАПЛАСА
ДЕТЕРМИНИЗМ (от англ. determine - определять) – учение
о всеобщей причинной обусловленности и закономерности явлений
Случайность полностью исключена. Все
в мире предопределено предшествующими состояниями
Слайд 25ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Импульс мат. точки –
это векторная величина:
Система материальных точек имеет импульс:
Импульс замкнутой системы
материальных точек не изменяется во времени
Слайд 27РАБОТА И МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Энергией называется скалярная физическая величина, являющейся
общей мерой различных форм движения материи. Энергия системы количественно характеризует
последнюю в отношении возможных в ней превращений движения.
Слайд 29КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Физическая величина, равная половине произведения массы тела на квадрат
его скорости, называется кинетической энергией тела:
Свойство. Аддитивность кинетической энергии
Слайд 30ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
это часть энергии механической системы, зависящая только от ее
конфигурации и от их положения во внешнем потенциальном поле.
Пример 1:
потенциальная энергия тела в поле тяготения:Пример 2: потенциальная энергия упругой деформации пружины:
Слайд 31ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Механическая энергия системы
это сумма кинетической и потенциальной энергии:
Консервативная система: все действующие на
нее непотенциальные силы работы не совершают, а все внешние потенциальные силы стационарны ПРИ ДВИЖЕНИИ КОНСЕРВАТИВНОЙ СИСТЕМЫ ЕЕ МЕХАНИЧЕСКАЯ ЭНЕРГИЯ НЕ ИЗМЕНЯЕТСЯ
Слайд 32МЕХАНИЧЕСКАЯ РАБОТА
Работой силы F на бесконечно малом перемещении ds называется
скалярная величина
в случае конечного перемещения:
Слайд 34ОСОБЕННОСТИ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Момент силы относительно неподвижной точки
Главный момент
системы сил
Слайд 35ОСОБЕННОСТИ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Момент импульса материальной точки относительно неподвижной точки
Момент импульса системы точек
Слайд 36ОСОБЕННОСТИ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Момент инерции материальной точки относительно неподвижной оси
Момент импульса системы материальных точек
Слайд 38ТЕОРЕМА ГЮЙГЕНСА-ШТЕЙНЕРА
Момент инерции тела относительно какой либо оси равен моменту
инерции его относительно параллельной оси, проходящей через центр масс, сложенному
с величинойгде а – расстояние между осями
Слайд 43СЛЕДСТВИЯ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- РЕЛЯТИВИСТСКОЕ ЗАМЕДЛЕНИЕ ВРЕМЕНИ
- РЕЛЯТИВИСТСКОЕ СОКРАЩЕНИЕ ДЛИНЫ
Слайд 45ЗАКОН ВЗАИМОСВЯЗИ МАССЫ И ЭНЕРГИИ
МАССА тела характеризует его инертность и
способность к гравитационному взаимодействию
ЭНЕРГИЯ способна превращаться из одной формы в
другуюВыражение внутренней сущности материи:
E = mc2
Слайд 47ДВА ПОДХОДА К ИССЛЕДОВАНИЮ ТЕПЛОВЫХ ЯВЛЕНИЙ
Термодинамика – это
наука о тепловых явлениях. Термодинамика исходит из наиболее общих закономерностей
тепловых процессов и свойств макроскопических систем. Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества.
Слайд 48ДВА ПОДХОДА К ИССЛЕДОВАНИЮ ТЕПЛОВЫХ ЯВЛЕНИЙ
Молекулярно-кинетической теорией называют
учение о строении и свойствах вещества на основе представления о
существовании атомов и молекул как наименьших частиц химического вещества
Слайд 49ОПИСАНИЕ ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
термодинамические системы – макроскопические объекты (тела и поля),
которые могут обмениваться энергией как друг с другом, так и
с внешней средойосновные макроскопические параметры ТС:
P – давление
V – объем
T - температура
Слайд 50РАВНОВЕСИЕ и ПРОЦЕСС
Термодинамическое равновесие характеризуется постоянством всех макроскопических параметров системы
При
изменении одного или нескольких параметров система переходит в новое состояние
равновесияТермодинамическое уравнение состояния:P = f (V, T)
Слайд 51ИДЕАЛЬНЫЙ ГАЗ
идеальный газ – это газ, взаимодействие между молекулами которого
пренебрежимо мало. Многие газы при нормальных условиях хорошо описываются такой
модельюуравнение состояния идеального газа:
Слайд 52ИЗОПРОЦЕССЫ
- это процессы, при протекании которых сохраняется хотя бы один
из макроскопических параметров
изотермическим процессом называют квазистатический процесс, протекающий при постоянной
температуре T. 
Слайд 57БАЗОВЫЕ ПОЛОЖЕНИЯ МКТ
Все вещества – жидкие, твердые и газообразные –
образованы из мельчайших частиц – молекул, которые сами состоят из
атомов («элементарных молекул»).Атомы и молекулы находятся в непрерывном хаотическом движении.
Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.
Слайд 58ВНУТРЕННЯЯ ЭНЕРГИЯ
все макроскопические тела обладают энергией, заключенной внутри самих этих
тел
внутренняя энергия вещества складывается из кинетической энергии всех атомов
и молекул и потенциальной энергии их взаимодействия друг с другом 
Слайд 59ВНУТРЕННЯЯ ЭНЕРГИЯ
является однозначной функций состояния термодинамической системы
U = f (V,
T)
внутренняя энергия идеального газа зависит только от температуры
Внутренняя
энергия одноатомного идеального газа:
Слайд 60КОЛИЧЕСТВО ТЕПЛОТЫ И РАБОТА
Количеством теплоты Q, полученной телом, называют изменение
внутренней энергии тела в результате теплообмена.
работа газа определяется выражением
Слайд 63ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Количество теплоты, полученное системой, идет на изменение ее
внутренней энергии и совершение работы над внешними телами.
Слайд 64ТЕПЛОЕМКОСТЬ
Если в результате теплообмена телу передается некоторое количество теплоты, то
внутренняя энергия тела и его температура изменяются.
Отношение количества теплоты
dQ, переданной телу к вызванному этим приращению температуры dT называют теплоемкостью вещества C 
Слайд 65ВИДЫ ТЕПЛОЕМКОСТИ
Удельная теплоемкость относится к массе вещества (Дж/кг)
Молярная теплоемкость относится
к количеству вещества (Дж/моль)
По отношению к процессу:
Сp –
теплоемкость при постоянном давленииСv - теплоемкость при постоянном объеме
Слайд 66КЛАССИЧЕСКАЯ ТЕОРИЯ ТЕПЛОЕМКОСТИ (Л. Больцман)
Теорема о равномерном распределении энергии по
степеням свободы
Если система молекул находится в тепловом равновесии
при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна kT/2
Слайд 69ЦИКЛИЧЕСКИЕ ПРОЦЕССЫ
- это такая совокупность термодинамических процессов, в результате
которых система возвращается в исходное состояние
Слайд 71ОБРАТИМЫЕ ПРОЦЕССЫ
Обратимыми процессами называют процессы перехода системы из одного равновесного
состояния в другое, которые можно провести в обратном направлении через
ту же последовательность промежуточных равновесных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию
Слайд 72ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Невозможен процесс, единственным результатом которого была бы передача
энергии путем теплообмена от тела с низкой температурой к телу
с более высокой температурой (Клаузиус)коэффициент полезного действия машины, работающей по циклу Карно, максимален
Слайд 73ЭНТРОПИЯ
это функция состояния термодинамической системы, изменение которой в обратимом процессе
при переходе из одного равновесного состояния в другой равно
Слайд 74ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ (закон неубывания энтропии)
При любых процессах, протекающих в
термодинамических изолированных системах, энтропия либо остается неизменной, либо увеличивается.
Вероятностная трактовка
2-го начала термодинамики:S = k* lnw
Слайд 75ЭЛЕКТРОДИНАМИКА
Электрический заряд – это физическая величина, характеризующая свойство частиц или
тел вступать в электромагнитные силовые взаимодействия
Существует два рода электрических
зарядов, условно названных положительными и отрицательными 
Слайд 77ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
в изолированной системе алгебраическая сумма зарядов всех
тел остается постоянной
Слайд 78ЗАКОН КУЛОНА
Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов
и обратно пропорциональны квадрату расстояния между ними:
Слайд 79ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
каждое заряженное тело создает в окружающем пространстве электрическое поле.
напряженность электрического поля – векторная физическая величина равная
Слайд 83ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА
Поток вектора напряженности электростатического поля через произвольную замкнутую
поверхность определяется алгебраической суммой зарядов, расположенных внутри этой поверхности:
Слайд 84ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
равен работе, которую совершают электрические силы при удалении
единичного положительного заряда из данной точки в бесконечность
Слайд 89ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
физическая величина, равная отношению модуля напряженности
внешнего электрического поля в вакууме к модулю напряженности полного
поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества.
Слайд 91ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ
Электроемкостью системы из двух проводников называется физическая
величина, определяемая как отношение заряда q одного из проводников к
разности потенциалов Δφ между ними
Слайд 94ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
энергия поля конденсатора
энергия электрического поля
объемная плотность энергии поля
Слайд 96ЗАКОН ОМА (для участка цепи)
сила тока I, текущего
по однородному металлическому проводнику (т. е. проводнику, в котором не действуют
сторонние силы), пропорциональна напряжению U на концах проводника:
Слайд 97ЭЛЕКТРОДВИЖУЩАЯ СИЛА
физическая величина, равная отношению работы сторонних сил
при перемещении заряда q от отрицательного полюса источника тока к
положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
Слайд 101ПРАВИЛА КИРХГОФА
1 правило: алгебраическая сумма сил токов для каждого узла
в разветвленной цепи равна нулю (следствие закона сохранения заряда)
2 правило:
алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура. 
