Слайд 1Теория вероятностей и математическая статистика
Случайные величины
Слайд 2Одномерные случайные величины
Пусть есть случайный эксперимент, Ω ─
пространство элементарных событий.
Определение
Случайной величиной ξ называется функция, отображающая Ω
в R.
ξ: Ω → R
(То есть ξ = ξ(ω)).
Смысл: случайная величина – это числовая функция, принимающая значения случайным образом.
Слайд 3Дискретные распределения
Определение
Случайная величина ξ имеет дискретное распределение, если она принимает
не более чем счетное число значений.
Значения: a1, a2,…,
Вероятности значений: pi = P(ξ = ai) > 0
Слайд 4Определение
Если случайная величина ξ имеет дискретное распределение, то рядом распределения
называется соответствие ai ↔pi, которое имеет вид :
Слайд 5Пример
Подбрасываем 1 раз кубик. Пусть Ω={1,2,3,4,5,6}, и две функции
из Ω в R заданы так: ξ(ω) = ω и
η(ω) = ω2. Построить ряды распределения.
Решение
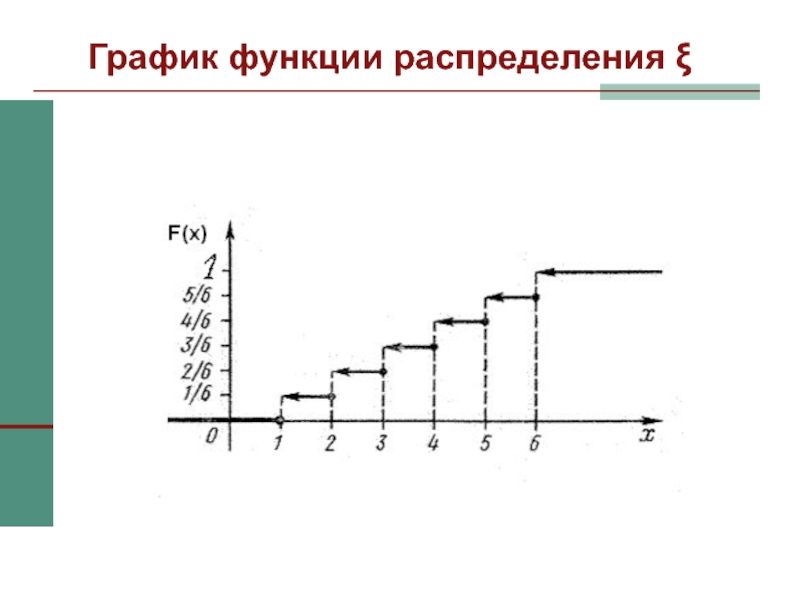
Слайд 6Графическое задание ряда распределения ξ
Слайд 7Примеры дискретных распределений
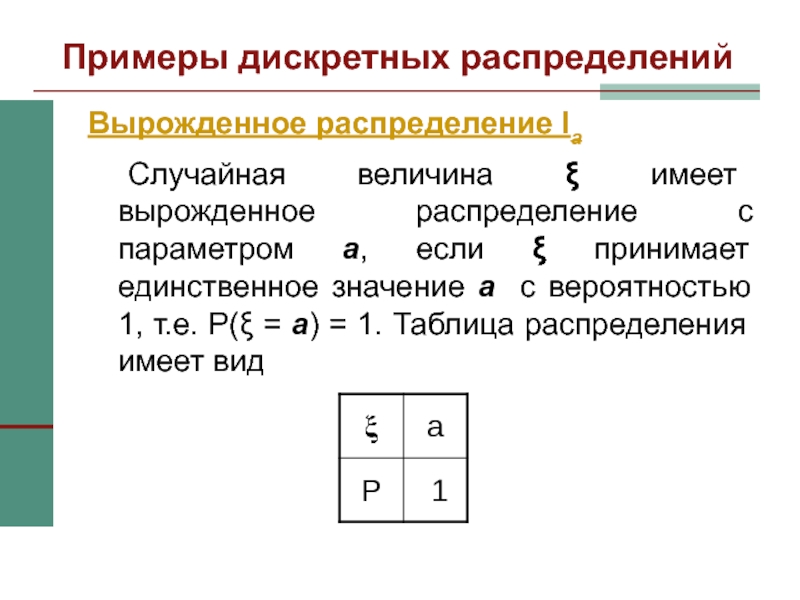
Вырожденное распределение Ia
Случайная величина ξ имеет вырожденное распределение
с параметром a, если ξ принимает единственное значение a с
вероятностью 1, т.е. P(ξ = a) = 1. Таблица распределения имеет вид
Слайд 8Дискретное равномерное распределение
Случайная величина ξ имеет дискретное равномерное распределение, если
ξ принимает n значений х1, х2,..., xn с вероятностями рi
= 1/n.
Слайд 9Распределение Бернулли Bp
Случайная величина ξ имеет распределение Бернулли с параметром
p, если ξ принимает значения 1 и 0 с вероятностями
p и q = 1 – p, соответственно.
Случайная величина ξ с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха p (0 успехов или 1 успех).
Слайд 10Биномиальное распределение B(n,p)
Случайная величина ξ имеет биномиальное распределение с параметрами
n и p, где 0 ≤ p ≤ 1, если
ξ принимает значения 0, 1, 2, …n с вероятностями P{ξ = k} = Cnk pk q n –k.
Случайная величина с таким распределением имеет смысл числа успехов в n испытаниях схемы Бернулли с вероятностью успеха p.
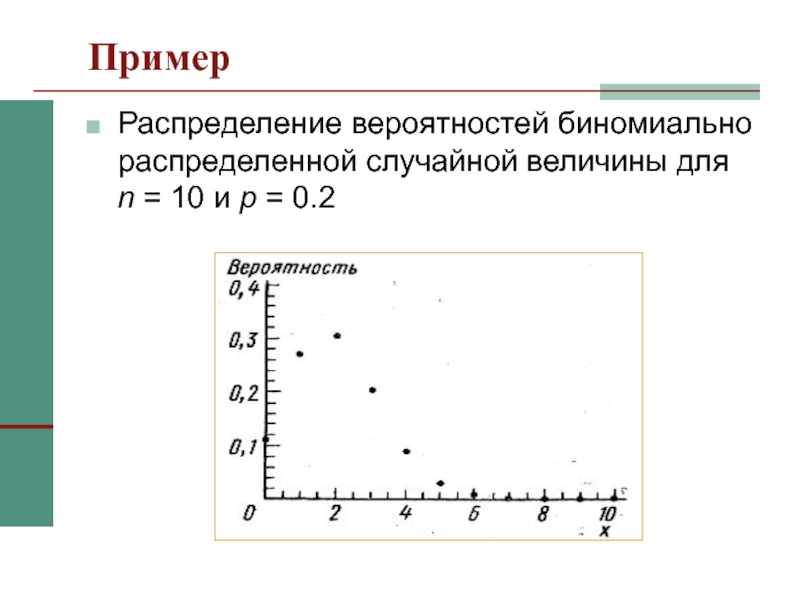
Слайд 11Пример
Распределение вероятностей биномиально распределенной случайной величины для n = 10
и p = 0.2
Слайд 12Геометрическое распределение Gp,
Сл.в. ξ имеет геометрическое распределение с параметром
p, где 0≤p≤1, если ξ принимает значения 1, 2, 3,…
с вероятностями P{ξ = k} = pqk –1.
Случайная величина ξ с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха p.
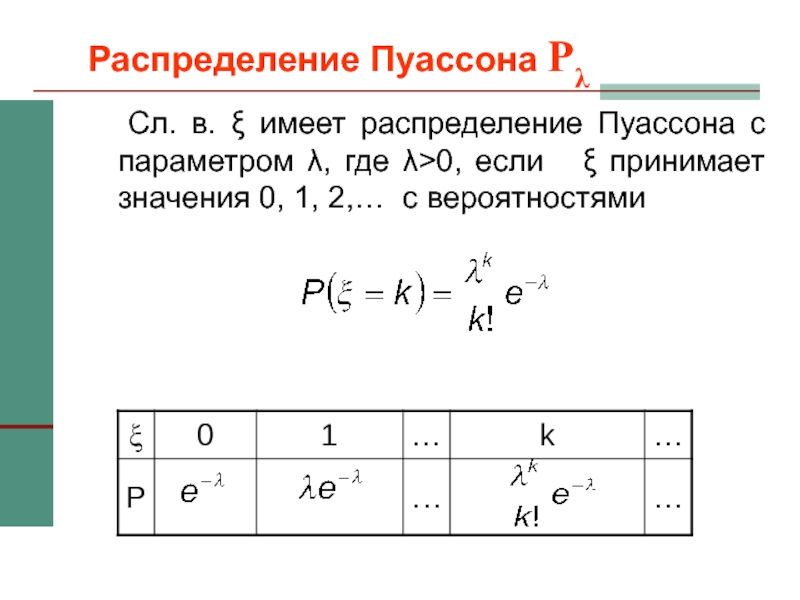
Слайд 13Распределение Пуассона Pλ
Сл. в. ξ имеет распределение Пуассона с
параметром λ, где λ>0, если ξ принимает значения 0,
1, 2,… с вероятностями
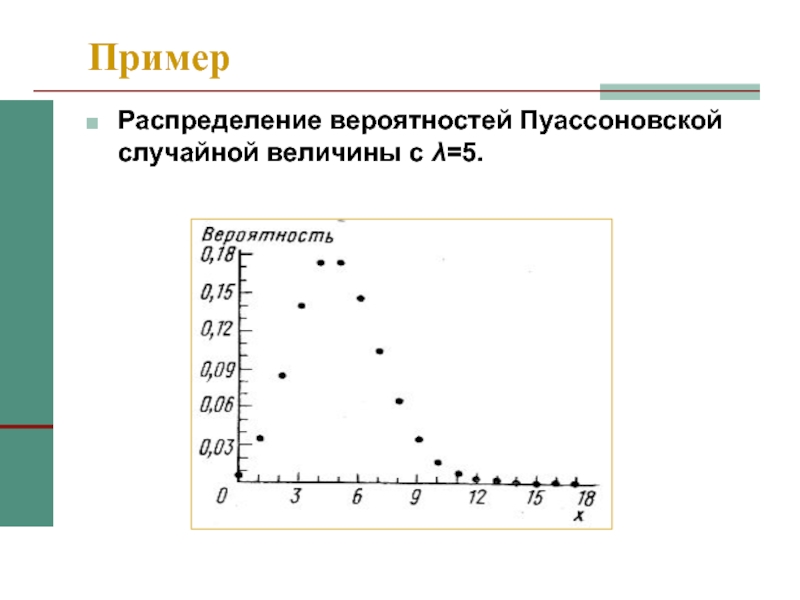
Слайд 14Пример
Распределение вероятностей Пуассоновской случайной величины с λ=5.
Слайд 15Распределение Пуассона
Это одно из важнейших дискретных вероятностных распределений впервые было
исследовано в 1837 г. С.Пуассоном (французский математик, механик и физик,
1781 – 1840 гг.)
Пуассоновская модель обычно описывает схему редких событий: при некоторых предположениях о характере процесса появления случайных событий число событий, происшедших за фиксированный промежуток времени или в фиксированной области пространства, часто подчиняется пуассоновскому распределению.
Слайд 16Распределение Пуассона
Примерами могут служить число частиц радиоактивного распада, зарегистрированных счетчиком
в течении некоторого времени t, число вызовов, поступивших на телефонную
станцию за время t, число дефектов в куске ткани или в ленте фиксированной длины, число изюминок в кексе и т.д. Наконец, распределение Пуассона дает хорошую аппроксимацию биномиального распределения для больших значений n и малых значений р.
Слайд 17Гипергеометрическое распределение
Сл.в. ξ имеет гипергеометрическое распределение с параметрами n, N
и K, где n ≤ N, K ≤ N, если
ξ принимает целые значения k с вероятностями
Случайная величина ξ с таким распределением имеет смысл числа белых шаров среди n шаров, выбранных наудачу без возвращения из урны, содержащей K белых шаров и N –K не белых.
Слайд 18Функция распределения
Определение
Функцией распределения случайной величины ξ называется функция Fξ(x),
при каждом
x∈R равная
Fξ(x) = P{ξ < x}.
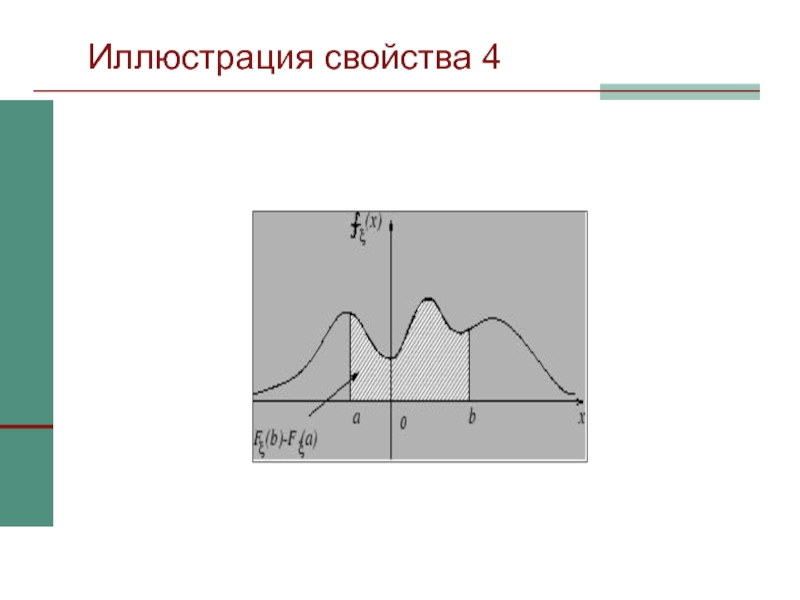
Слайд 22Свойства функции распределения
1) Функция распределения Fξ(x) не убывает: если x1
то Fξ(x1) ≤ Fξ(x2);
2) Существуют пределы
3) Функция распределения
непрерывна слева:
Слайд 23Непрерывные распределения
Определение
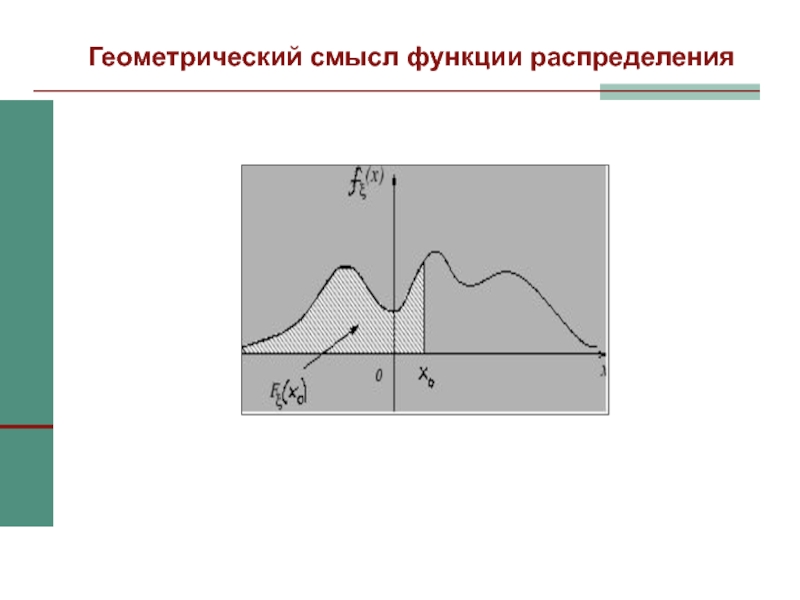
Случайная величина ξ имеет абсолютно непрерывное распределение, если
существует неотрицательная функция fξ(x) такая, что для любого x0∈R функция
распределения представима в виде
При этом функция fξ(x) называется плотностью распределения случайной величины ξ.
Слайд 24Геометрический смысл функции распределения
Слайд 26Замечание
Термин для «почти всех» означает «для всех, кроме (возможно)
x из некоторого множества нулевой меры (длины)». Заметьте, что стоящую
под интегралом функцию можно изменить в одной точке (или на множестве нулевой длины), и интеграл от этого не изменится.
Слайд 28Примеры непрерывных распределений
Равномерное распределение R [a, b]
Слайд 29График плотности распределения R[a,b]
Слайд 30График функции распределения R[a,b]
Слайд 31
С помощью линейного преобразования
приводится к равномерному распределению на отрезке [0,1].
Равномерное распределение является непрерывным аналогом распределений классической теории вероятностей, описывающих
случайные эксперименты с равновероятными исходами.
Погрешность, происходящая от округления числа, удовлетворительно описывается равномерным распределением на отрезке [ –1/2, 1/2].
Слайд 32Нормальное распределение N (a,σ)
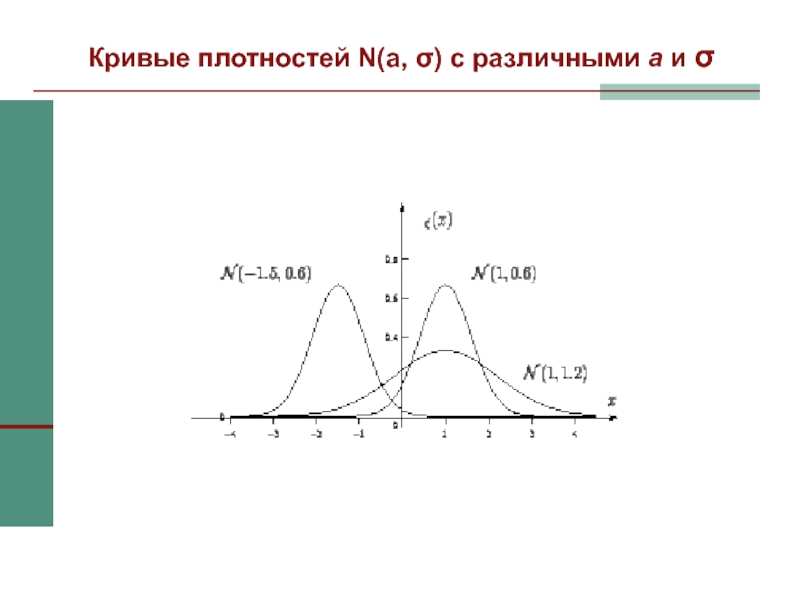
Слайд 33Кривые плотностей N(a, σ) с различными а и σ
Слайд 34Нормальное распределение N (a,σ)
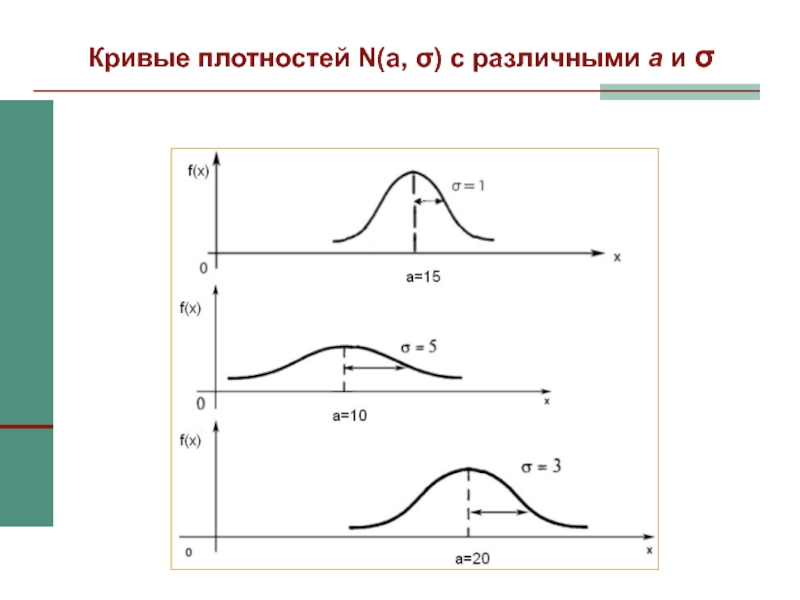
Графики нормальных плотностей имеют симметричную, колоколообразную форму.
а – это величина, которая характеризует положение кривой плотности на
оси абсцисс.
Изменение σ приводит к изменению формы кривой плотности, с увеличением σ кривая делается менее островершинной и более растянутой вдоль оси абсцисс.
Слайд 35Кривые плотностей N(a, σ) с различными а и σ
Слайд 36Интерпретация
С помощью модели нормального распределения можно описать множество явлений, например
распределение высоты деревьев, площадей садовых участков, массы тела людей, дневной
температуры и т. д. Нормальное распределение используется и для решения многих проблем в экономической жизни. Например, распределение числа дневных продаж в магазине, числа посетителей универмага в неделю, числа работников в некоторой отрасли, объемов выпуска продукции на предприятии и т. д.
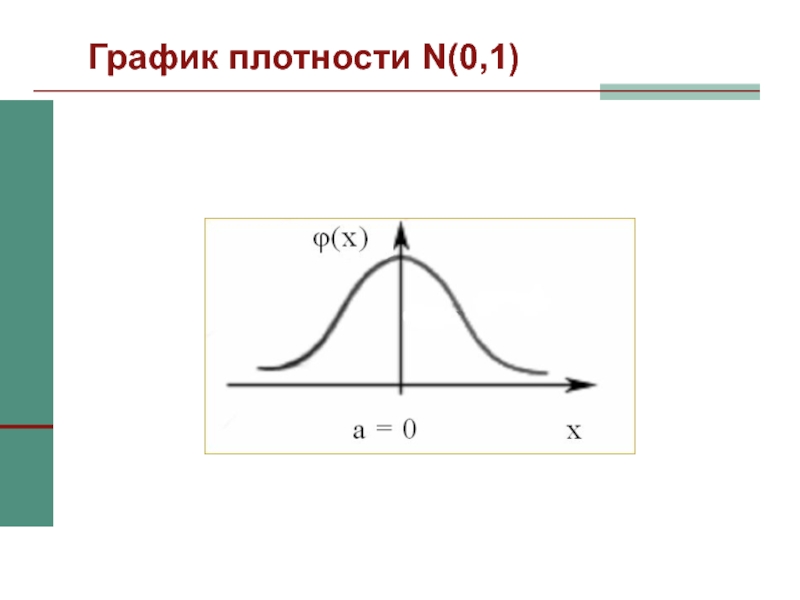
Слайд 37N(0,1)
При а = 0 и σ = 1 нормальное распределение
называют стандартным нормальным распределением
Слайд 39Плотность и функция распределения N(0,1)
Слайд 40Нормальное распределение N (a, σ)
Фундаментальная роль, которую играет нормальное распределение,
объясняется тем, что при широких предположениях суммы случайных величин с
ростом числа слагаемых ведут себя асимптотически нормально.
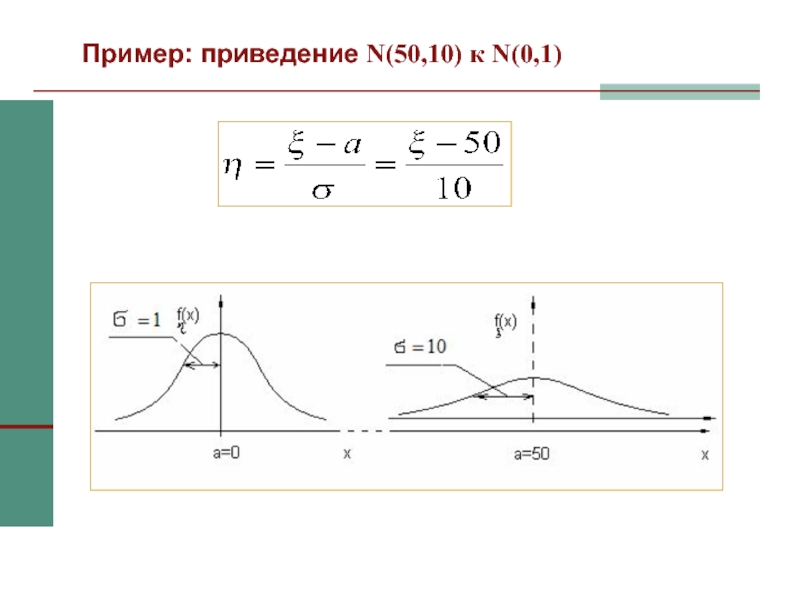
С помощью линейного преобразования
нормальное распределение с произвольными параметрами (a, σ) приводится к нормальному распределению с параметрами (0, 1).
Слайд 41Пример: приведение N(50,10) к N(0,1)
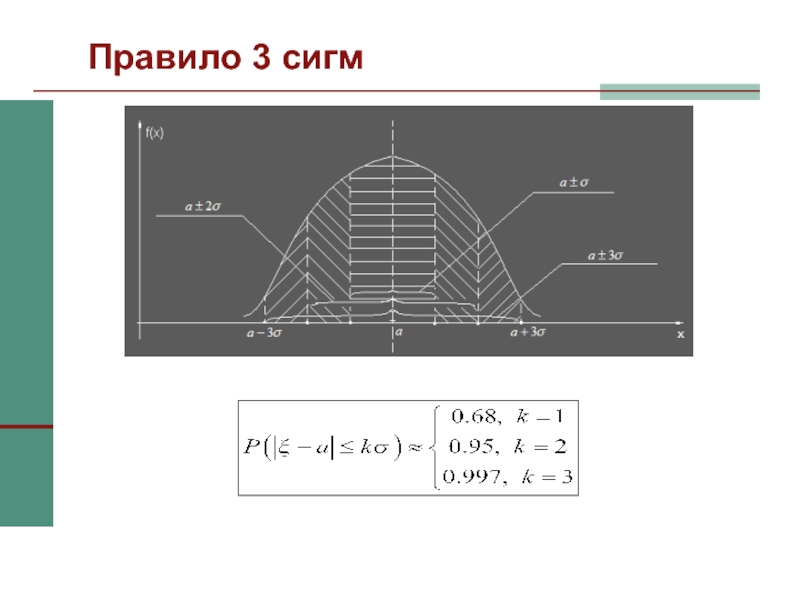
Слайд 42Правило 3 сигм
Нормально распределенная случайная величина с большой вероятностью принимает
значения, близкие к своему математическому ожиданию, что выражается правилом сигм:
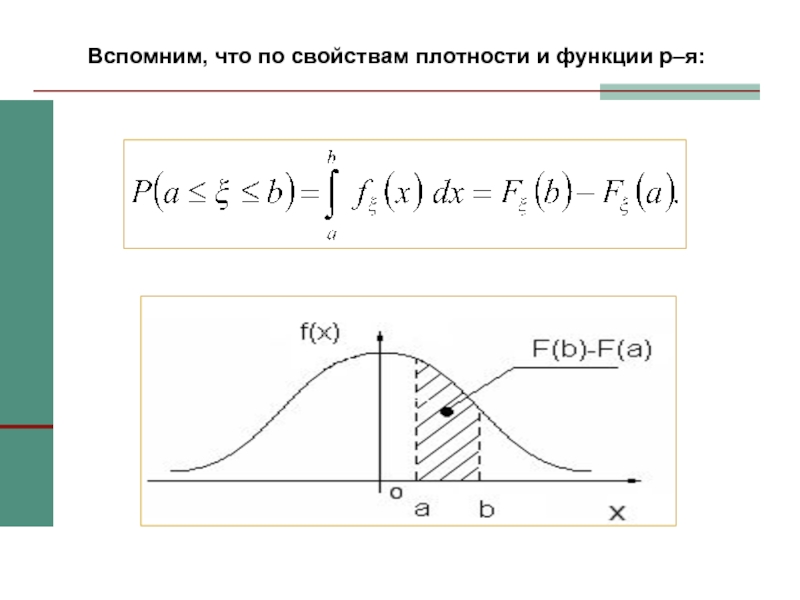
Слайд 43Вспомним, что по свойствам плотности и функции р–я:
Слайд 45Показательное (экспоненциальное) распределение Eλ
Плотность и функция распределения Eλ
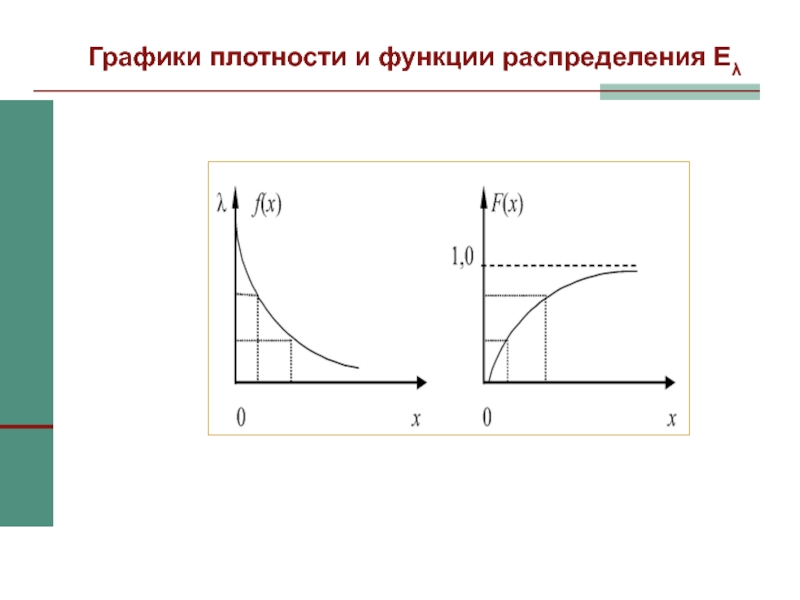
Слайд 46Графики плотности и функции распределения Eλ
Слайд 47Графики плотности и функции распределения E2
Слайд 48Свойства распределения Eλ
Это распределение является непрерывным аналогом геометрического распределения.
Обладает
свойством отсутствия последействия
в связи с чем является основным в теории
скачкообразных марковских процессов.
Слайд 49Плотность распределения Коши
Распределение Коши
Слайд 50Плотность Гамма –распределения
Г –распределение
Слайд 51Гамма –распределение
Г–распределение является непрерывным аналогом отрицательного биномиального распределения.
При α =
1 совпадает с показательным.
При α = n/2, λ = 1/2
совпадает с X2 –распределением с n числом степеней свободы.
При λ = nμ, α = n называется эрланговским распределением с параметрами (n,μ) и описывает распределение длительности интервала времени до появления n событий процесса Пуассона с параметром μ, используемым в теории массового обслуживания и теории надежности.
Слайд 52Плотность распределения Лапласа
Распределение Лапласа (двойное экспоненциальное распределение)
Слайд 53Многомерные СВ
Определение
n – мерной случайной величиной ξ называется вектор
ξ(ω)=(ξ1(ω),
ξ2(ω), … , ξn(ω)),
компонентами которого являются одномерные случайные величины.
Слайд 54Определение
Функцией распределения n–мерной случайной величины ξ называется функция
Fξ1,ξ2,…,ξn(x1, x2,
…, xn)=
=P(ξ1 < x1, ξ2 < x2,…, ξn
xn)
Слайд 55Свойства функции распределения
1) 0 ≤ Fξ1,ξ2,…,ξn(x1,x2,…,xn) ≤ 1,
2) Существуют пределы
3) Функция
распределения Fξ(x) непрерывна слева.
Слайд 56Определение
Случайная величина ξ имеет непрерывное n –мерное распределение, если существует
неотрицательная функция fξ1,ξ2,…,ξn(x1,x2,…,xn) такая, что для любого x ∈
Rn функция распределения представима в виде
![Примеры непрерывных распределенийРавномерное распределение R [a, b]](/img/thumbs/d3f412ab76021b9cb9b832aeea97ef5f-800x.jpg "Случайные велечины Примеры непрерывных распределенийРавномерное распределение R [a, b]")
![График плотности распределения R[a,b]](/img/tmb/2/140744/0986b1f76059d68cbfb0ac2808907e66-800x.jpg "Случайные велечины График плотности распределения R[a,b]")
![График функции распределения R[a,b]](/img/thumbs/59f7f4b7db1865b0296284abb0e89a8c-800x.jpg "Случайные велечины График функции распределения R[a,b]")
![С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное распределение является непрерывным аналогом распределений классической](/img/thumbs/cc96f16953c6b544911d3e1aa4578d10-800x.jpg "Случайные велечины С помощью линейного преобразования приводится к равномерному распределению на отрезке [0,1]. Равномерное")
