Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Смежные углы
Содержание
- 1. Смежные углы
- 2. Дорогу осилит идущий, геометрию – думающий.Девиз урока:
- 3. Цель урока:1. Изучить новый вид углов;2. Научить
- 4. Оборудование урока: Урок презентация на тему:
- 5. С каким настроением вы пришли сегодня на урок?
- 6. "Ты - мне, я - тебе, я - вам, вы - мне!"! ! !? ? ?
- 7. Повторение изученного материала:Какие виды углов вы знаете?
- 8. АксиомыАксиома – утверждение, не требующее доказательствСамо слово
- 9. Теорема.Утверждение, которое требуется доказать, называется теоремой.Теорема состоит
- 10. «Открытие» нового знания. Ввести понятие смежного угла;Научить
- 11. Смежные углы Сумма смежных углов равна
- 12. Теорема. Сумма смежных углов равна 180..1) Так
- 13. Если два угла равны, то смежные
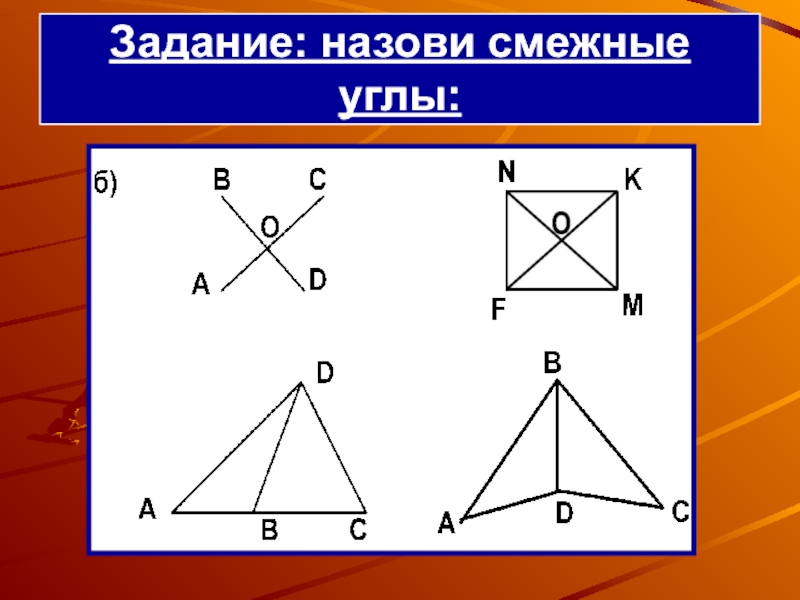
- 14. Задание: назови смежные углы:
- 15. Как записать решение ? Дано:
- 16. Алгебраический метод решения геометрических задач.Найдите смежные
- 17. Пусть x – коэффициент пропорциональности, тогда, BOC
- 18. Работа по учебникуСтраница -26, задача к п.14, №1(у.), №4 (1,) (п).
- 19. Тест по теме: «Смежные углы»1. Если один
- 20. Проверь себя!1) Б; 2) А; 3) В;4)* В.
- 21. Итог урока:1. Заполните пропуски так, чтобы верными
- 22. Проверь себя!А – общая… полупрямыми.Б -
- 23. Рефлексия деятельности Что нового вы узнали на
- 24. Какое сейчас у вас настроение?
- 25. Домашнее задание: §2, п14, теорема2.1(у) задачи: №2
- 26. «Если бы мне пришлось начать вновь своё
- 27. СПАСИБО ЗА УЧАСТИЕ,ЦАРИЦА "МАТЕМАТИКА" ВАС ЖДЕТ В ГОСТИСпасибо за урок! До свидания!
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 «Смежные углы»
Автор – учитель математики
МОУ СОШ№5
Цуканова Зоя Ивановна.
нельзя есть за границей?Слайд 3Цель урока:
1. Изучить новый вид углов;
2. Научить учащихся правильно рассуждать
– доказывать теорему;
3. Знать следствия из доказанной теоремы;
4. Выработать навыки
применения теоремы и следствий в ходе решения задач.Прививать любовь к геометрии.
Слайд 4 Оборудование урока:
Урок презентация на тему: «Смежные углы»;
Компьютер и
мультимедийный проектор
Таблица смежных углов;
Тетради и учебные принадлежности;
Оценочные листы.
Слайд 7Повторение изученного материала:
Какие виды углов вы знаете?
Какой угол называется
развёрнутым?
Какое высказывание древних математиков вы связываете с определением теоремы?
В каких единицах измеряются углы?Чем измеряются углы?
Что написал ученикам великий Платон над своей дверью?
Слайд 8Аксиомы
Аксиома – утверждение, не требующее доказательств
Само слово « аксиома »
происходит от греческого «аксиос», что означает «ценный, достойный». Древнегреческий ученый
Евклид первым придумал аксиомы, которые были изложены в его знаменитом сочинении «Начала».Слайд 9Теорема.
Утверждение, которое требуется доказать, называется теоремой.
Теорема состоит из трёх частей:
1.Условие (дано), 2.Заключение (что требуется доказать), 3.Доказательство.
Слайд 10«Открытие» нового знания.
Ввести понятие смежного угла;
Научить строить угол, смежный
с данным;
Научить находить на чертеже смежные углы;
Правильно сформулировать и
доказать теорему о смежных углах;Разобрать следствия из этой теоремы;
Ввести понятие алгебраического метода решения геометрических задач.
Слайд 11Смежные углы
Сумма смежных углов
равна 180˚
Два угла
называются смежными, если у них одна сторона общая, а другие
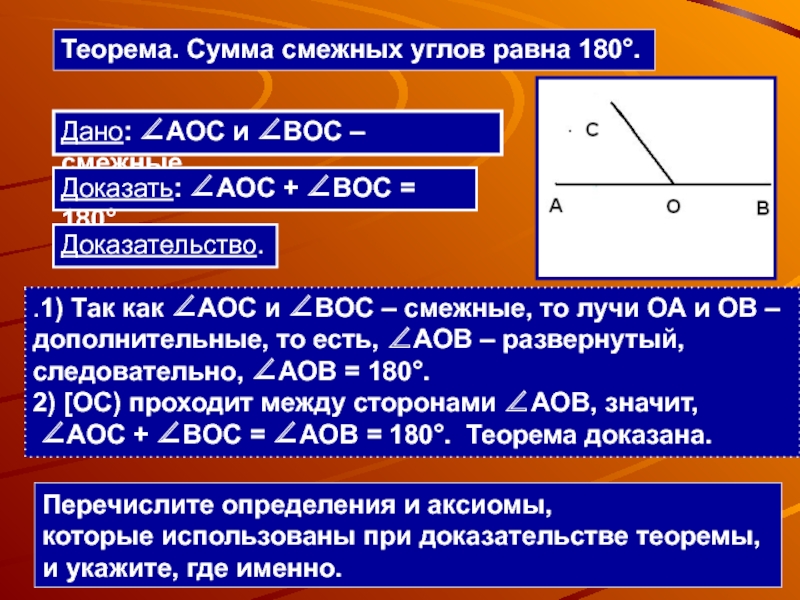
стороны этих углов являются дополнительными полупрямыми.Слайд 12Теорема. Сумма смежных углов равна 180.
.1) Так как AOC и
BOC – смежные, то лучи ОА и ОВ – дополнительные,
то есть, AOB – развернутый, следовательно, AOB = 180.2) [OC) проходит между сторонами AOB, значит,
AOC + BOC = AOB = 180. Теорема доказана.
Дано: AOC и BOC – смежные.
Доказать: AOC + BOC = 180
Доказательство.
Перечислите определения и аксиомы,
которые использованы при доказательстве теоремы,
и укажите, где именно.
Слайд 13 Если два угла равны, то смежные с ними углы
равны.
2) Угол, смежный прямому углу – прямой.
3) Угол смежный острому
углу – тупой,смежный тупому углу – острый.
4) Если угол не развёрнутый, то его градусная мера меньше 180˚
Следствия из теоремы
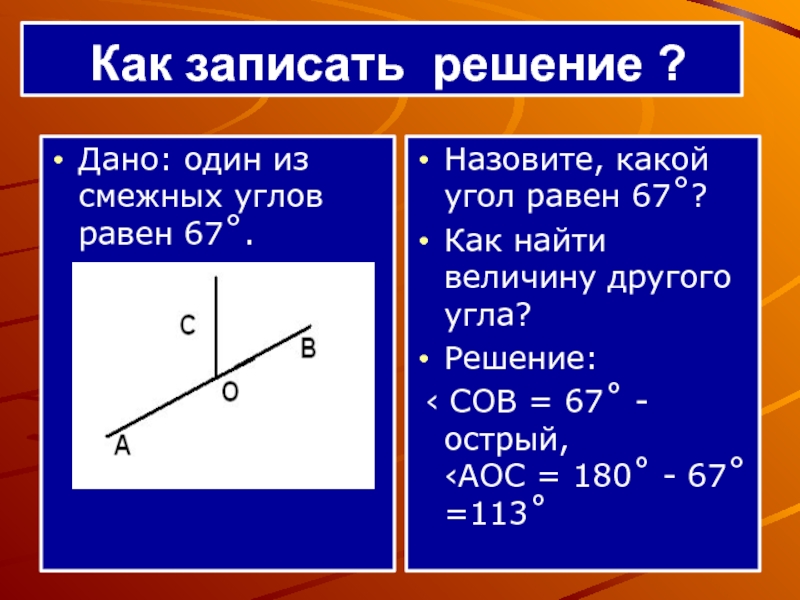
Слайд 15 Как записать решение ?
Дано: один из смежных
углов равен 67˚.
Назовите, какой угол равен 67˚?
Как найти величину другого
угла? Решение:
‹ СОВ = 67˚ - острый, ‹АОС = 180˚ - 67˚ =113˚
Слайд 16 Алгебраический метод решения геометрических задач.
Найдите смежные углы, если один
из них в 3 раза больше другого.
Решение:
Х + 3Х =
180, 4Х = 180, Х = 45.Меньший угол, <АОС = 45˚, больший угол, < СОВ = 3∙45=135˚
Слайд 17
Пусть x – коэффициент пропорциональности,
тогда, BOC = 25x; AOВ
= 11x.
Так как AOВ + BOC = 180,
то
11x + 25x = 180; 36x = 180;
x = 5.
Следовательно, BOC = 125; AOВ= 55.
Дано: AOВ и BOC – смежные;
BOC : AOВ = 25:11
Найти: AOВ; BOC.
Решение.
Слайд 19Тест по теме: «Смежные углы»
1. Если один из смежных углов
острый, то другой тоже острый.
А) да-острый; Б) нет - тупой;
В) нет- прямой.2. Сумма смежных углов равна 180˚.
А) да - 180˚; Б) нет - 90˚, В) нет - 360˚.
3)Если каждый из двух углов прямой, то они смежные.
А) нет - тупые; Б) нет – развёрнутые;
В) да – смежные.
4)* Один из смежных углов в 8 раз больше другого. Найдите больший из этих углов.
А) 120˚; Б) 140˚ ; В) 160.˚
Слайд 21Итог урока:
1. Заполните пропуски так, чтобы верными были формулировки:
А) Два
угла называются смежными, если у них одна сторона _______, а
две другие являются дополнительными __________.Б) Угол, равный 90˚, называется ___________.
В) Сумма смежных углов равна _____________.
Г)* Если один из смежных углов равен 130˚, то другой _______.
Д)* Если на часах 6 часов, то часовая и минутная стрелка образуют ____________________ угол.
Е) *Угол смежный с тупым углом, есть ____________ угол.
Слайд 22Проверь себя!
А – общая… полупрямыми.
Б - прямым.
В - 180˚.
Г*
- 50˚.
Д* - развёрнутый угол.
Е* - острый.
Слайд 23Рефлексия деятельности
Что нового вы узнали на уроке?
Что повторили?
Каким
методом мы можем решать геометрические задачи?
Чью активную работу вы
можете сегодня отметить?Как оцениваете свою работу?
Какое у вас сейчас настроение?
Слайд 25Домашнее задание: §2, п14, теорема2.1(у)
задачи: №2 (у), №3(п),
№4( 4)*(п)
Придумать несколько примеров , где вы наблюдаете в жизни
применение смежных углов.Геометрия