Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Спецкурс Математическое моделирование в гуманитарных науках Лекция 2
Содержание
- 1. Спецкурс Математическое моделирование в гуманитарных науках Лекция 2
- 2. Методологический постулат о нестационарной компоненте социальных процессовПроцессы
- 3. Зависимость класса математической модели от типа объекта
- 4. Базовая математическая модель социального процессаДискретная динамическая система
- 5. Слайд 5
- 6. Тезис А.Ляпунова о корректности формулирования моделиМатематическими объектами
- 7. Условие корректности задания моделиОна должна быть «грубой»
- 8. Определение блуждающих и не блуждающих точекРассматриваем систему
- 9. Центральные движенияМножество M1 может рассматриваться как фазовое
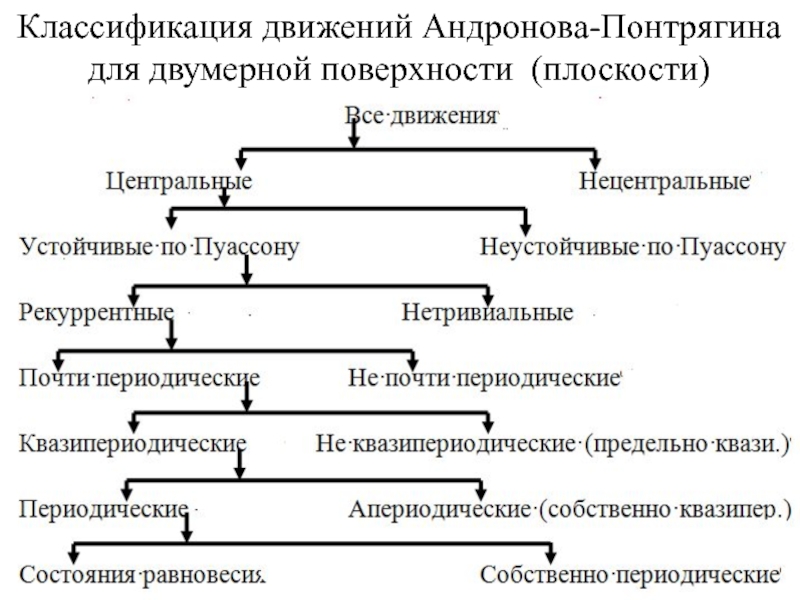
- 10. Классификация движений Андронова-Понтрягина для двумерной поверхности (плоскости)
- 11. Определение. Точка x0 называется устойчивой по Пуассону
- 12. Теорема Пуанкаре о возвращении как следствие существования инвариантной меры у эндоморфизма Т
- 13. Ступени стохастичностиСуществование у преобразования Т инвариантной мерыСуществование
- 14. Инвариантная мера как проявление стационарности (пример существования)
- 15. Доказательство существования инвариантной меры для Т - преобразования
- 16. Слайд 16
- 17. Слайд 17
- 18. Эргодичность как следствие перемешивания
- 19. Выполнение центральной предельной теоремы –Ц.П.Т.
- 20. Экспоненциальное убывание корреляций (эук) Существует q, 0
- 21. Теорема 7.1 (Андронов–Понтрягин). Система X является грубой
- 22. социальные
- 23. Слайд 23
- 24. Слайд 24
- 25. Постановка задачи и вывод системы ОДУ базовой
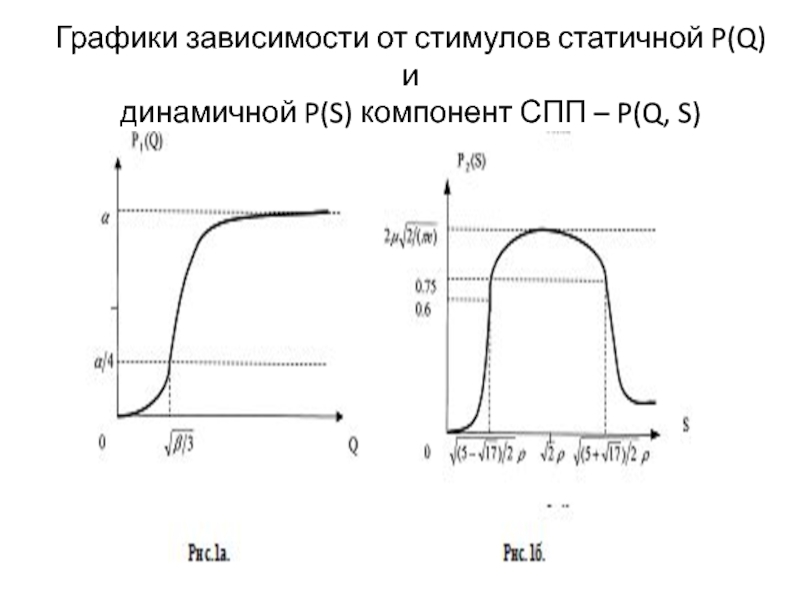
- 26. Графики зависимости от стимулов статичной P(Q) и динамичной P(S) компонент СПП – P(Q, S)
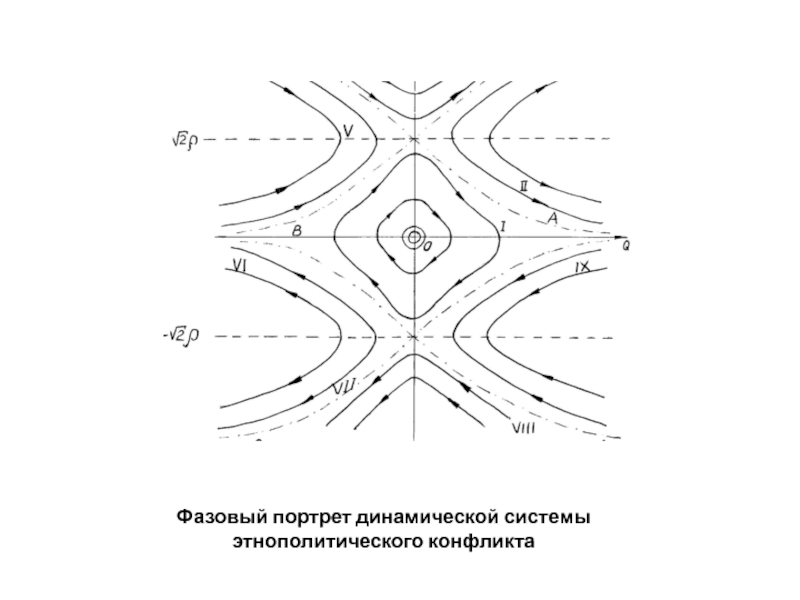
- 27. Фазовый портрет динамической системы этнополитического конфликта
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Модель К.Левина жизненного пространства личности (ЖПЛ) L
- 38. Построение символьной г.д.с. Шаг 1Обозначим каждый регион
- 39. Построение символьной г.д.с. Шаг 2Пусть на фазовом
- 40. Построение символьной г.д.с. Шаг 3Отождествим ЖПЛ с
- 41. Построение символьной г.д.с. Шаг 4Пусть ω0 –
- 42. Построение символьной г.д.с. Шаг 5 Применение теста Колмогорова
- 43. Библиография1. П.Биллингслей. Эргодическая теория и информация. –
- 44. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Методологический постулат о нестационарной компоненте социальных процессов
Процессы в естественных науках
породили представления об устойчивых стационарных моделях как основе описания явлений
мира:Существующее устойчиво
Исследования сложных систем в науках о живой материи (биологии, физиологии, психологии и т.д.) и неравновесных процессов в физике, физи- ческой химии обосновали заглавный постулат:
Предсказуемость существующего
Слайд 3Зависимость класса математической модели от типа объекта первичной идеализации (ОПИ)
и цели решаемой задачи
Любой конкретный социальный процесс имеет конечные
временные рамки: сроки возникновения и завершения.Внутри этого интервала времени может быть выбран такой срок, в пределах которого структура отношений между факторами неизменна, а т.е. возможны такие постановки задач, для которых имеет содержательный смысл стационарная модель (см).
В случае, когда в рамках некоторого подинтервала времени проис-
ходят перестройки структуры социального процесса, то логично определиться с нестационарной моделью (нм).
Нестационарная модель может оказаться устойчивой, частично устойчивой и неустойчивой в соответствии с типом процесса.
Все эти классы моделей приемлемы в сфере задач прогнозирования, если число обусловленности матрицы оператора модели < 500
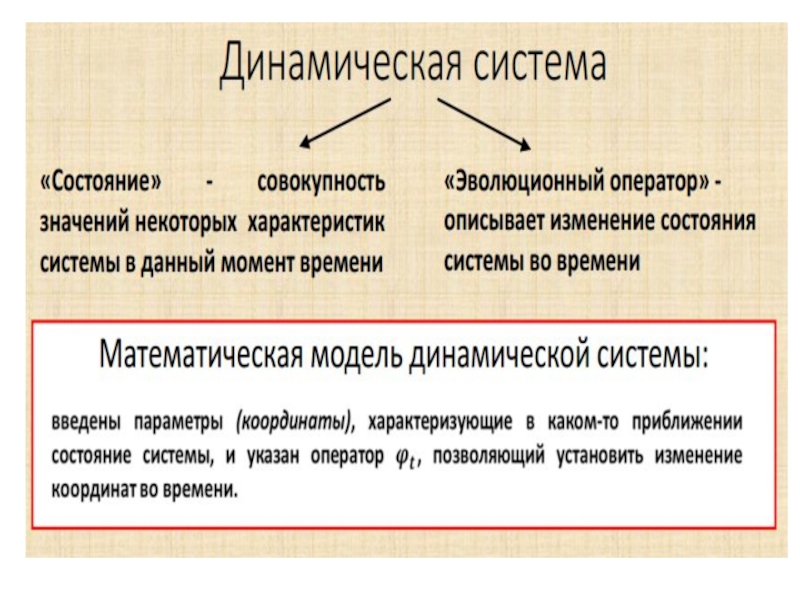
Слайд 4Базовая математическая модель социального процесса
Дискретная динамическая система - Д.Д.С.:
Xn+1 =
A(Xn, Xn-1,…, Xn-m), где Xn – вектор в k –
мерном признаковом пространстве с метрикой не хуже, чем в интервальных шкалах, n – дискретное время, т.е. это СРС – система рекуррентных соотношений с m – лагом.Условием перехода СРС в конечно-разностные уравнения (КРУ) являются требования (на примере 2-х слойной схемы; рассматриваются также модели процессов с числом слоев ≤ 3):
Xn+1 = Xn + τ*F(tn, Xn), где tn = n*τ
Условием перехода КРУ в ОДУ – обыкновенные дифференциальные уравнения является существование конечного предела:
lim (Xn+1 - Xn )/(tn+1 - tn ) при (tn+1 - tn) 0
Слайд 6Тезис А.Ляпунова о корректности формулирования модели
Математическими объектами нелинейной динамики являются
модели — явно заданные динамические системы, зависящие от конечного числа
параметров. Важнейшим требованием к модели является то, что она должна правильно, по крайней мере качественно, описывать природу соответствующего физического или социально-экономического явления.В связи с этим вспомним следующее замечание, сделанное Ляпуновым: «. . . нельзя использовать сомнительные аргументы при решении конкретной проблемы, не важно механики или физики, если она задана корректно с математической точки зрения. С того момента, как система определена, она становится предметом чистого анализа и ее нужно трактовать только таким образом».
Дом. задание: привести пример некорректной модели
Слайд 7Условие корректности задания модели
Она должна быть «грубой» или структурно устойчивой,
т.е. не менять свой топологический тип фазовой диаграммы при «малом
шевелении» векторного поля д.с.Дано множество двумерных систем на плоскости,
заданных уравнением x˙ = X(x), где X(x1, x2) — Сr -гладкая (r ≥1) функция, определенная в замкнутой ограниченной области G ⊂ R2.
Определение 7.1. Динамическая система X называется грубой в области G, если для любого ε > 0 существует такое δ > 0, что
все системы в δ-окрестности X топологически эквивалентны X;
гомеоморфизм, который устанавливает эту эквивалентность, является ε-близким к тождественному (то есть расстояние между двумя соответствующими точками меньше, чем ε)
При этом δ-окрестность системы X как множество всех систем X1, удовлетворяющих
условию ||X1 − X ||C1 < δ, где
На множестве введена следующая норма : || X || C1 = sup ( ||X || +|| ∂X/ ∂x|| ) .
x∈G
Л.П.Шильников, А.Л.Шильников, Д.В.Тураев, Л.Чуа. Методы качественной теории в нелинейной динамике, часть 2, Москва-Ижевск, 2009
Слайд 8Определение блуждающих и не блуждающих точек
Рассматриваем систему x˙ = X(x),
где X ∈ C1 в ограниченной и замкнутой области G
⊂ Rn, границы которой состоят из гладких (n − 1)-мерных поверхностей без контакта с векторным полем, ориентированным внутрь, G.Следовательно, для любой точки x0 ∈ G положительная полутраектория x(t, x0) определена при любой начальной точке x0.
Определение 7.3. Точка x0 называется блуждающей, если у нее существует такая окрестность U(х), что при некотором T > 0 и всех t >T U(х) ∩ x(t, U) = ∅.
Здесь, как и ранее: x(t, U) = U x(t, ξ).
ξ∈U
Из определения следует, что каждая точка ξ ∈ U также является блуждающей. Поэтому множество всех блуждающих точек открыто. Кроме того, легко видеть, что если точка x0 — блуждающая, то точка x(t, x0) также блуждающая для любого t.
Из открытости множества блуждающих точек вытекает, что его дополнение – множество неблуждающих точек М1 замкнуто.
Слайд 9Центральные движения
Множество M1 может рассматриваться как фазовое пространство динамической системы,
и поэтому можно повторить процедуру и построить множество M2, состоящее
из неблуждающих точек для системы, ограниченной на M1.Очевидно, что M2 ⊆ M1. Подобно M1, множество M2 также является компактным инвариантным множеством.
Если M2 = M1, то говорят, что M1 — центр или множество центральных движений. Ситуация в точности такова, когда мы рассматриваем грубые двумерные системы.
В общем случае имеем M1 ⊃ M2 ⊃ ... ⊃ Mk ⊃ ... Если Mk = Mk+1, начиная с некоторого k, тогда Mk также называется центром, а k называется порядковым числом центральных движений.
Слайд 11 Определение. Точка x0 называется устойчивой по Пуассону в положительном направлении
(P +-устойчивой), если существует такая последовательность tn, где tn →
+∞ при n → +∞, что lim n→+∞ x(tn, x0) = x0. Другими словами, точка x0 является ω-предельной*) точкой своей положительной полутраектории.Определение точки, устойчивой по Пуассону в отрицательном направлении, аналогично вышеприведенному за исключением того, что tn → −∞. В случае когда точка одновременно P +-устойчива и P −-устойчива, говорят, что она устойчива по Пуассону.
Устойчивые по Пуассону траектории могут быть, в свою очередь, разделены на два типа в зависимости от того, ограничена или нет последовательность {τk(ε)} времен возвращения Пуанкаре P-траектории в ее ε-окрестность. Биркгоф называл траектории первого типа рекуррентными траекториями.
*) Точку х* называют ω – предельной точкой траектории L, если для некоторой
Последовательности {t k}, где t k→∞, lim (t k) = х* при k→∞
Устойчивость по Пуассону
Слайд 12Теорема Пуанкаре о возвращении как следствие существования инвариантной меры у
эндоморфизма Т
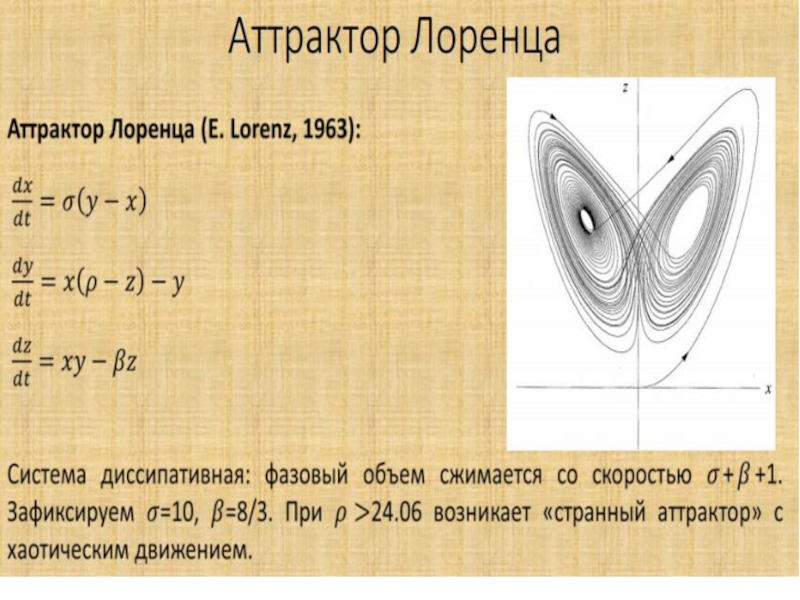
Слайд 13Ступени стохастичности
Существование у преобразования Т инвариантной меры
Существование у преобразования Т
средней по траектории (т. Биркгофа-Хинчина)
Равенство средней по траектории для Т
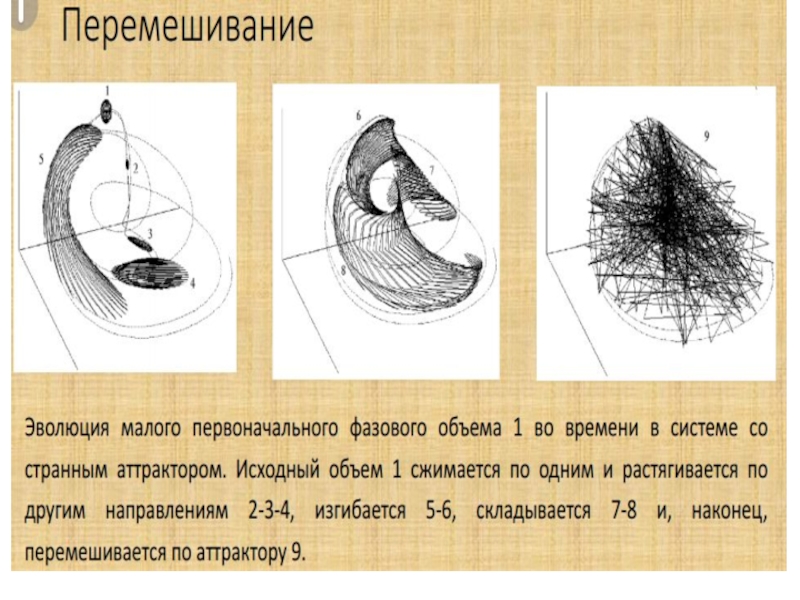
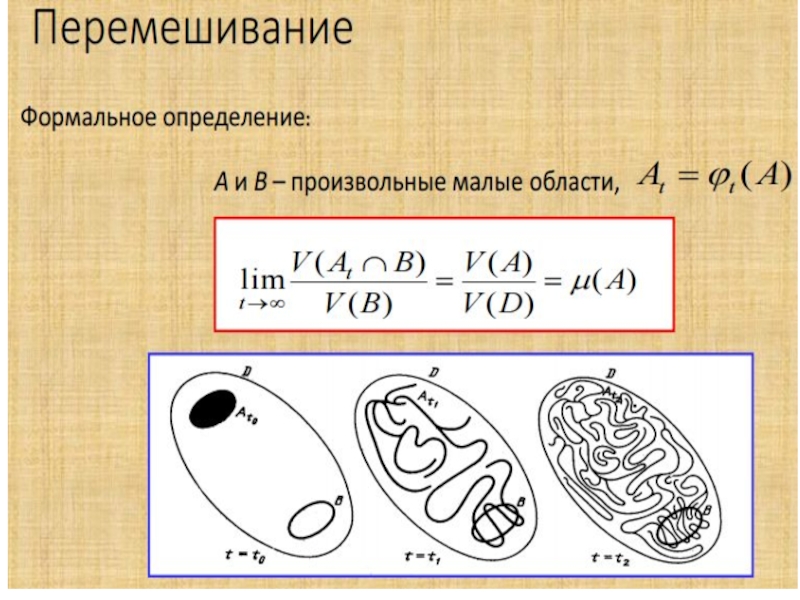
среднему по (М, М, μ)Существование слабого перемешивания – сходимости по Чезаро, т.е. в квадратичной степени
Существование сильного перемешивания
Выполнение ЦПТ –центральной предельной теоремы
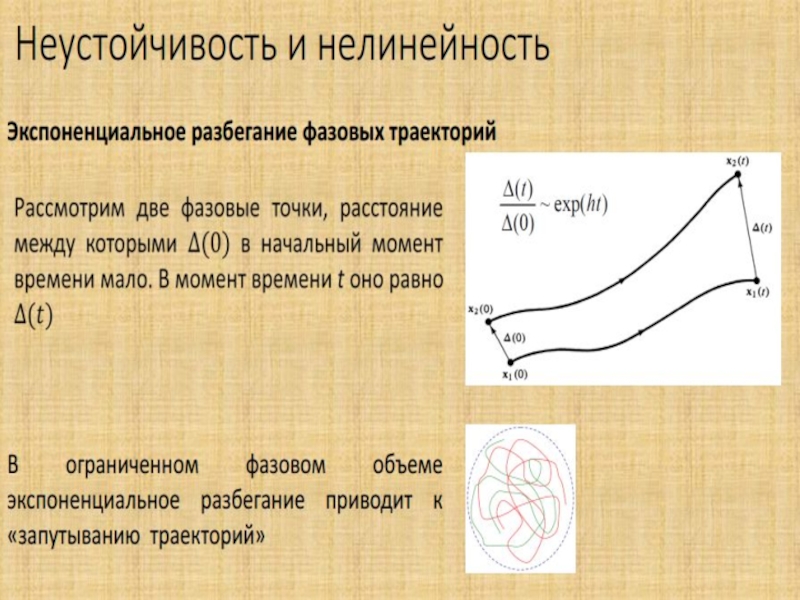
Экспоненциальное убывание корреляций
Слайд 20Экспоненциальное убывание корреляций (эук)
Существует q, 0 < q < 1
такое, что
|∫(f(Tk x))f(x)dμ(x)|≤ C(f)qk (*)
Группа (Tk ) обладает свойством (эук), если (*)
имеет место для достаточно богатого запаса функций.
Слайд 21Теорема 7.1 (Андронов–Понтрягин). Система X является грубой в области G
тогда и только тогда, когда
(1) не существует состояний равновесия
с характеристическим показателем на мнимой оси; (2) не существует периодических орбит с мультипликатором на единичной окружности и
(3) не существует сепаратрис, идущих из седла в другое (или то же самое) седло.
Последнее условие может быть переформулировано как отсутствие гомоклинических и гетероклинических траекторий. Из приведенной выше теоремы следует, что грубая система на плос- кости может обладать только грубыми состояниями равновесия (узлами, фокусами и седлами) и грубыми предельными циклами и их конечное число.
Теорема Андронова-Понтрягина
Слайд 25Постановка задачи и вывод системы ОДУ
базовой модели динамики этноконфликта
Q =
c (X0 - Y0) + c (X1 - Y1),
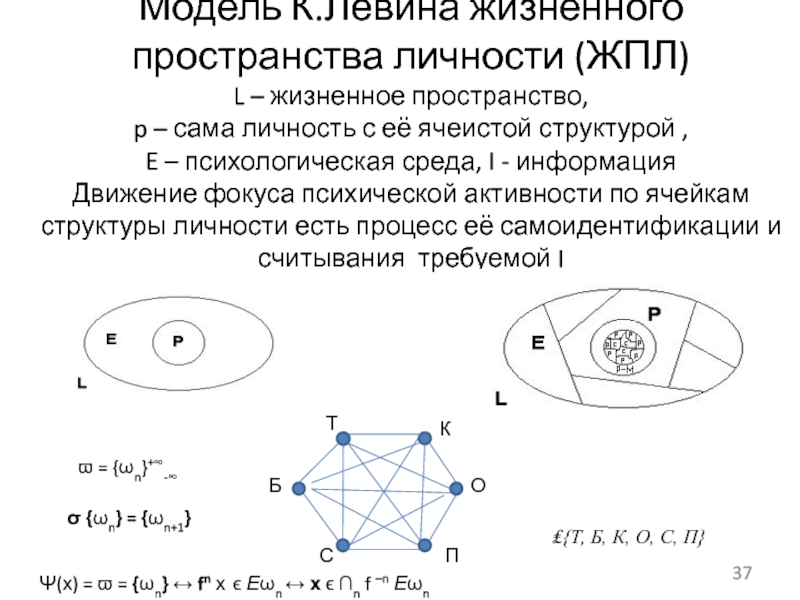
Слайд 37Модель К.Левина жизненного пространства личности (ЖПЛ) L – жизненное пространство, p
– сама личность с её ячеистой структурой , E –
психологическая среда, I - информация Движение фокуса психической активности по ячейкам структуры личности есть процесс её самоидентификации и считывания требуемой IТ
Б
К
О
С
П
σ {ωn} = {ωn+1}
ϖ = {ωn}+∞-∞
Ψ(х) = ϖ = {ωn} ↔ fn х ϵ Еωn ↔ х ϵ ∩n f –n Еωn
₤{Т, Б, К, О, С, П}
Слайд 38Построение символьной г.д.с. Шаг 1
Обозначим каждый регион символом ωi ,
где
i = 1, 2, … n, т.е. тем самым вводим
буквыωn некоторого алфавита L.
- Рассмотрим пространства Σ последовательностей
ϖ = {ωn}+∞-∞
Изучаются каскады – дискретные динамические системы (д.д.с.), порождённые сдвигом σ в этих пространствах:
σ {ωn} = {ωn+1}
Слайд 39Построение символьной г.д.с. Шаг 2
Пусть на фазовом пространстве Х действует
д.д.с.: {fn ; n ϵ Z},
порождённая отображением
f: Х
ХЭта система строго детерминирована: задав х0 ,
однозначно получаем траекторию хn = fn х0 , n ϵ Z
Известно: и в социологии и в психологии существует массивное множество показателей, измеряемых в «слабых шкалах», т.е. физически не точно!
{ωn}
Слайд 40Построение символьной г.д.с. Шаг 3
Отождествим ЖПЛ с пространством Х, а
регионы, введённые К.Левином, с элементами его конечного покрытия, т.е.
Х =
Ȗi=1 Ei .Тогда при попадании точки д.д.с. х в Ei автоматически записывается значение i.
Слайд 41Построение символьной г.д.с. Шаг 4
Пусть ω0 – стартовое значение д.д.с.,
т.е. х0 ϵ Еω0 . Спустя
время t образ ft Еω0 множества Еω0 может весьма вытянуть ся и пересекать несколько Еi. , т.е. быть неоднозначным
Это не результат Случая, а в силу неточности задания х.
Регистрация автоматом для всех моментов времени значений ωi порождает отображение ψ: Х → Σ, сопоставляющее точке х последовательность ϖ так, что
Ψ(х) = ϖ = {ωn} ↔ fn х ϵ Еωn ↔ х ϵ ∩n f –n Еωn
Это основная догма символьной динамики
Слайд 42Построение символьной г.д.с. Шаг 5
Применение теста Колмогорова Мартина – Лёфа
для выделения последовательностей символов разного уровня сложности. Oценка меры
последовательностей μ Qn , выражающих периодические закономерности :где N1 – число гармоник в описании начального ансамбля (НА), Δω– означает радиус
окрестности около ωi, n – число, начиная с которого усложнение НА тождественно с
лучайному.
U + - характеристическая функция:
U +
Слайд 43Библиография
1. П.Биллингслей. Эргодическая теория и информация. – М.: «МИР», 1969
2. Синай Я.Г. Современные прблемы эргодической теории. –М.: ФИЗМАТЛИТ, 1995.
3.
Халмош П.Р. Лекции по эргодической теории. –Издательский Дом «Удмуртский университет», Ижевск, 19993. Л.П.Шильников, А.Л.Шильников, Д.В.Тураев, Л.Чуа. Методы качественной теории в нелинейной динамике, часть 1,2, Москва-Ижевск, 2004, 2009.
4. В.А. Шведовский, О.В. Шведовский. Тополого-сетевая модель жизненного пространства личности как обобщение гипотезы К.Левина // Математическое моделирование социальных процессов, вып.11, Сб. статей / Под ред. А.П. Михайлова. – М.: МАКС Пресс, 2010.- 176 с.