Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические критерии для простых экспериментальных схем
Содержание
- 1. Статистические критерии для простых экспериментальных схем
- 2. ЦелиПростейшие критерии для проверки гипотез
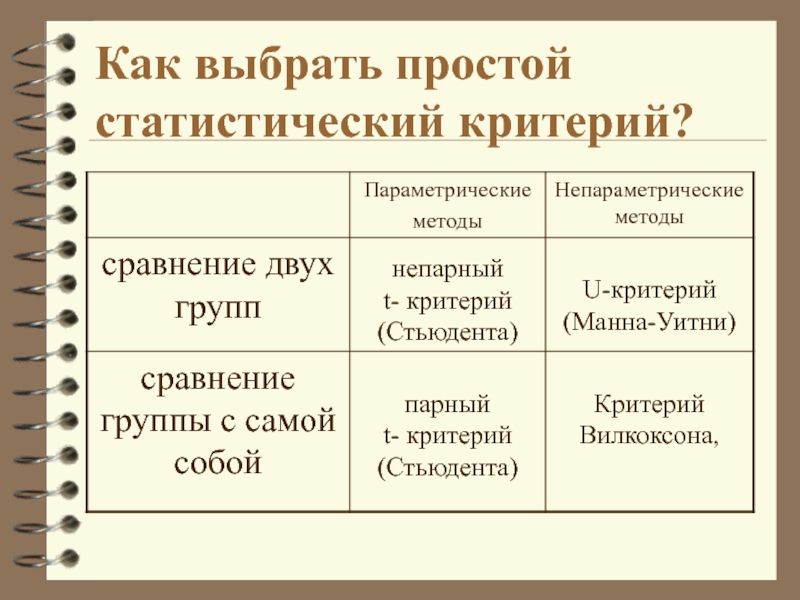
- 3. Как выбрать простой статистический критерий?
- 4. t-критерий Стьюдента (идея)У млекопитающих самцы весят больше, а у птиц - наоборот
- 5. t-критерий Стьюдента (идея)Насколько Вы уверены в своей
- 6. t-критерий Стьюдента (идея)Вы словили 5 самцов и
- 7. t-критерий Стьюдента (идея)Вы словили 100 самцов и
- 8. t-критерий Стьюдента (идея)Вы словили 100 самцов и
- 9. t-критерий Стьюдента (идея)
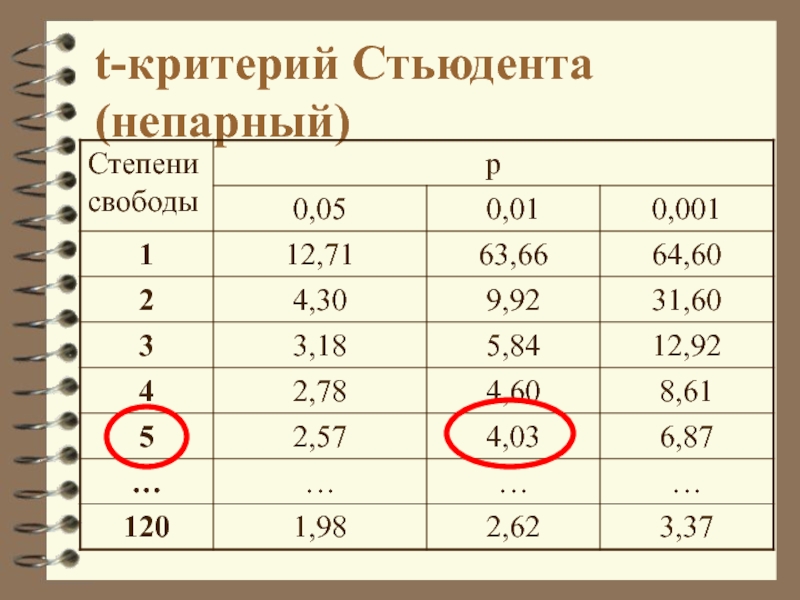
- 10. t-критерий Стьюдента (непарный)Проверяет гипотезу о том, что
- 11. t-критерий Стьюдента (непарный)Исходные предположения:1) Одна выборка извлекается
- 12. t-критерий Стьюдента (непарный)Исходные предположения:2) Распределение изучаемого признака
- 13. t-критерий Стьюдента (непарный)формулы
- 14. t-критерий Стьюдента (непарный)df=N+M-2 формулы
- 15. t-критерий Стьюдента (непарный)
- 16. t-критерий Стьюдента (парный)Проверяет гипотезу о том, что
- 17. t-критерий Стьюдента (парный)Исходные предположения:Каждому представителю одной выборки
- 18. t-критерий Стьюдента (парный)Исходные предположения:3) Распределение изучаемого признака
- 19. t-критерий Стьюдента (парный) df=N-1формулы
- 20. Критерий Манна-УитниПоказывает, насколько совпадают два ряда значений
- 21. где N1 - количество испытуемых в выборке
- 22. Критерий ВилкоксонаОснован на ранжировании абсолютных разностей пар
- 23. Критерий ВилкоксонаT=SRr где Rr - ранговые значения сдвигов с более редким знаком
- 24. Определить критерийДетский психолог хочет определить влияние матерчатых
- 25. Стой, Подумай,
- 26. Стой, Подумай,
- 27. Стой, Подумай,
- 28. Стой, Подумай,
- 29. ЦелиПростейшие критерии для проверки гипотез
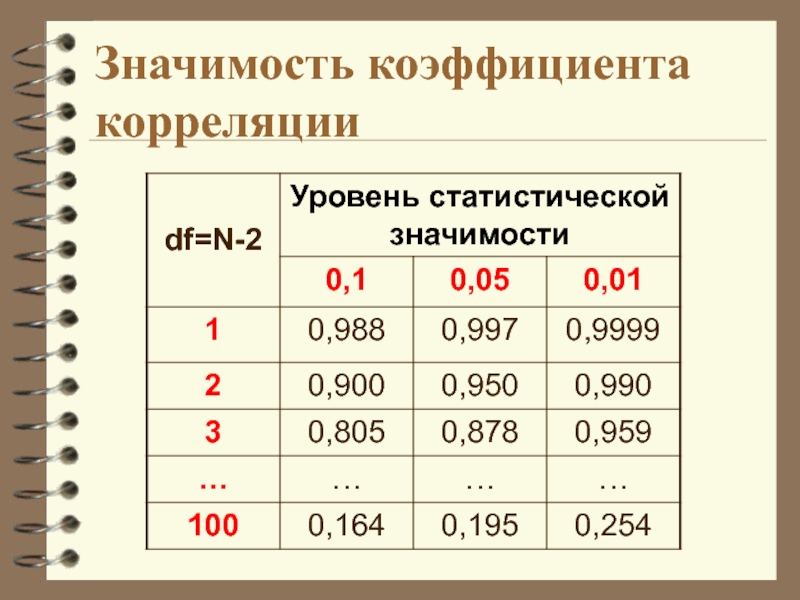
- 30. Значимость коэффициента корреляцииЭто уровень значимости, полученный при
- 31. Как определить?Отношение выборочного коэффициента корреляции к своей
- 32. Как определить?Нулевую гипотезу отвергают на принятом уровне
- 33. Как определить?Еще проще можно посмотреть в специальной таблице.
- 34. Значимость коэффициента корреляции
- 35. Корреляционная матрицаПримечание: * - p
- 36. СПАСИБО ЗА ВНИМАНИЕ!
- 37. Скачать презентанцию
ЦелиПростейшие критерии для проверки гипотез
Слайды и текст этой презентации
Слайд 1Статистические критерии
для простых экспериментальных схем
Статистические методы в психологии
Радчикова Н.П.
Слайд 5t-критерий Стьюдента (идея)
Насколько Вы уверены в своей гипотезе, если …
Вы
словили одного самца и одну самку. Самец весит больше.
Вы словили
всех самцов и всех самок. В среднем самцы весят больше.
Если всех словить невозможно, то сколько нужно словить животных, чтобы гипотеза подтвердилась?
Слайд 6t-критерий Стьюдента (идея)
Вы словили 5 самцов и 5 самок. Средний
вес самцов 10 кг, но среди них встречаются и 2-х,
и 18-ти килограммовые.Средний вес самок 9 кг, но среди них встречаются и 2-х, и 18-ти килограммовые.
Насколько Вы уверены в своей гипотезе?
Слайд 7t-критерий Стьюдента (идея)
Вы словили 100 самцов и 100 самок. Средний
вес самцов 10 кг, но среди них встречаются и 2-х,
и 18-ти килограммовые.Средний вес самок 9 кг, но среди них встречаются и 2-х, и 18-ти килограммовые.
Насколько Вы уверены в своей гипотезе?
Слайд 8t-критерий Стьюдента (идея)
Вы словили 100 самцов и 100 самок. Средний
вес самцов 10 кг, но среди них встречаются животные весом
от 9,8 до 10,2 кгСредний вес самок 9 кг, но среди них встречаются животные весом от 8,8 до 9,2 кг.
Насколько Вы уверены в своей гипотезе?
Слайд 10t-критерий Стьюдента (непарный)
Проверяет гипотезу о том, что средние значения двух
генеральных совокупностей, из которых извлечены сравниваемые независимые выборки, отличаются друг
от друга.
Слайд 11t-критерий Стьюдента (непарный)
Исходные предположения:
1) Одна выборка извлекается из одной генеральной
совокупности, а другая, независимая от первой, извлекается из другой генеральной
совокупности. Независимость означает, что представители двух выборок не составляют пары коррелирующих значений)
Слайд 12t-критерий Стьюдента (непарный)
Исходные предположения:
2) Распределение изучаемого признака и в той,
и в другой выборке приблизительно соответствует нормальному
3) Дисперсии признака в
двух выборках примерно одинаковы (гомогенны)
Слайд 16t-критерий Стьюдента (парный)
Проверяет гипотезу о том, что средние значения двух
генеральных совокупностей, из которых извлечены сравниваемые зависимые выборки, отличаются друг
от друга.
Слайд 17t-критерий Стьюдента (парный)
Исходные предположения:
Каждому представителю одной выборки (из одной генеральной
совокупности) поставлен в соответствие представитель другой выборки (из другой генеральной
совокупности)Данные двух выборок положительно коррелируют
Слайд 18t-критерий Стьюдента (парный)
Исходные предположения:
3) Распределение изучаемого признака и в той,
и в другой выборке соответствует нормальному закону
Слайд 20Критерий Манна-Уитни
Показывает, насколько совпадают два ряда значений измеренного признака.
Основная идея
основана на представлении всех значений двух выборок в виде одной
общей последовательности упорядоченных (ранжировнных) значений.Нуль-гипотезе соответствует ситуация, когда значения одной выборки будут равномерно распределены среди значений другой выборки
Слайд 21где N1 - количество испытуемых в выборке 1;
N2 - количество
испытуемых в выборке 2;
Tx - большая из двух ранговых сумм
Nx
- количество испытуемых в группе с большей суммой рангов.Критерий Манна-Уитни
Слайд 22Критерий Вилкоксона
Основан на ранжировании абсолютных разностей пар значений зависимых выборок.
Идея заключается в подсчете вероятности получения минимальной из положительной и
отрицательной разностей при условии, что распределение этих разностей равновероятно и равно ½.
Слайд 24Определить критерий
Детский психолог хочет определить влияние матерчатых и бумажных подгузников
на выработку навыков проситься на горшок. Однодневные младенцы будут использоваться
как испытуемые в начале проекта. Возраст, в котором подгузники не понадобятся (в течение недели) будет определен в конце эксперимента. Стой, Подумай, Примени
Слайд 25 Стой, Подумай, Примени
Определить критерий
Решено провести
исследование, ставящее своей задачей сравнить боязнь заразиться СПИДом ( по
7-балльной шкале) среди наркоманов и ненаркоманов.
Слайд 26 Стой, Подумай, Примени
Определить критерий
Проверяем, правда
ли то, что произнесение иностранных слов, вполне обычных по своему
значению, но фонетически схожих с табуированной лексикой родного языка человека, вызывает у него затруднения большие, чем произнесение табуированных слов чужого языка.
Слайд 27 Стой, Подумай, Примени
Определить критерий
Деканат сравнивает
оценки студентов по 5-балльной шкале полезности курсов «Основы мат. статистики»
и «Идеологии» для их дальнейшей проф. деятельности
Слайд 28 Стой, Подумай, Примени
Определить критерий
Студентки сравнивают
вес 5 подружек, худевших по кремлевской диете и 7 подружек,
худевших по пентагонской диете
Слайд 30Значимость коэффициента корреляции
Это уровень значимости, полученный при проверке
нуль-гипотезы о
равенстве нулю коэффициента корреляции между интересующими нас переменными
в генеральной
совокупности. 
Слайд 31Как определить?
Отношение выборочного коэффициента корреляции к своей ошибке служит критерием
для проверки нуль-гипотезы - предположения о том, что в генеральной
совокупности этот показатель равен нулю.
Слайд 32Как определить?
Нулевую гипотезу отвергают на принятом уровне значимости, если
Значения
критических точек tкр для разных уровней значимости и числа степеней
свободы N-2 ищем в таблице t-критерия
