Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические методы анализа данных
Содержание
- 1. Статистические методы анализа данных
- 2. Когда и зачем применяетсяПри наличии большого массива данных:Получение усредненных данныхОценка связей между переменнымиКлассификацияКластеризацияРедукция данных
- 3. Виды шкалНоминативная ИнтервальнаяРанговая (порядковая)Абсолютная (метрическая)
- 4. Основные понятия. Поиск среднего значения = меры центральной тенденцииМодаМедианаСреднее арифметическое
- 5. Выброс: Квантиль – точка на числовой оси,
- 6. Меры изменчивостиРазмах — разность между минимальным и
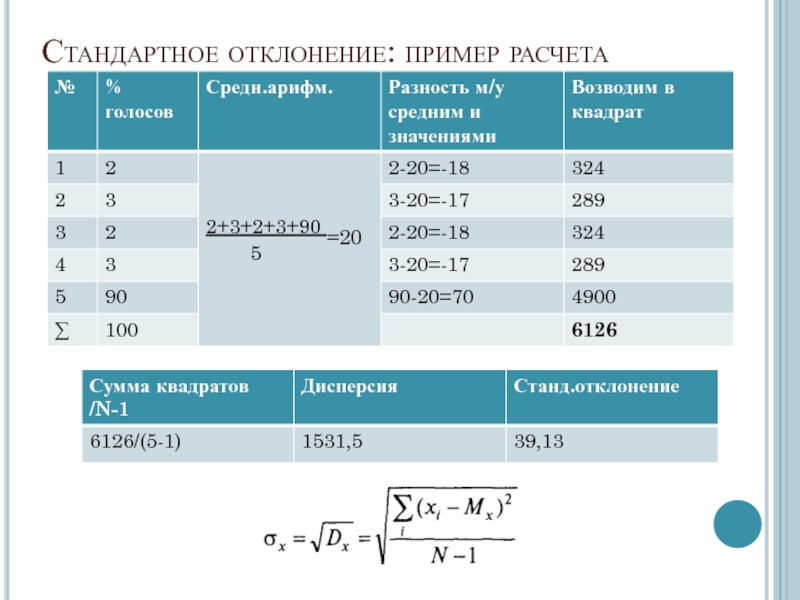
- 7. Стандартное отклонение: пример расчета
- 8. Закон нормального распределенияНормальное распределение признака можно определить,
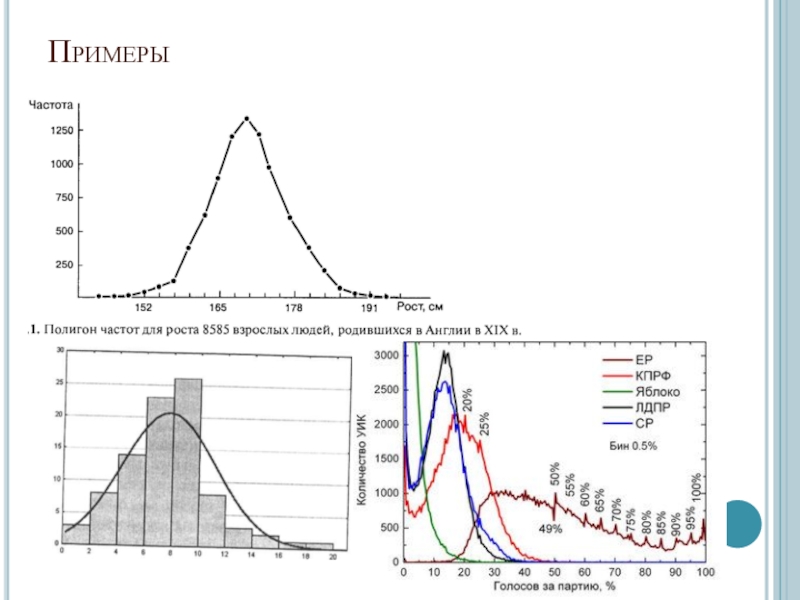
- 9. Примеры
- 10. Статистическая значимость В гумманитарных науках устанавливается, как
- 11. Χ-квадрат по Пирсону: наличие связи между переменнымиКритерий
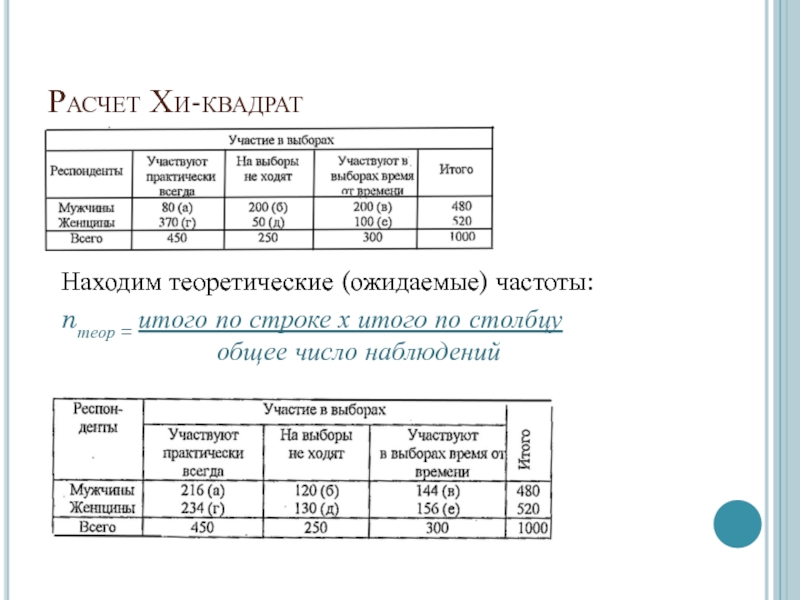
- 12. Расчет Хи-квадратНаходим теоретические (ожидаемые) частоты:nтеор = итого
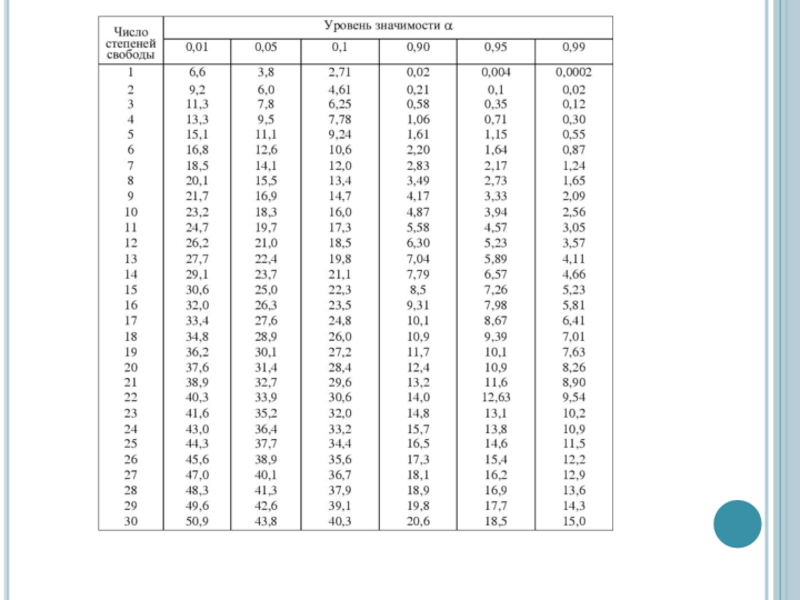
- 13. далее – сравнение с табличным критическим значением
- 14. Слайд 14
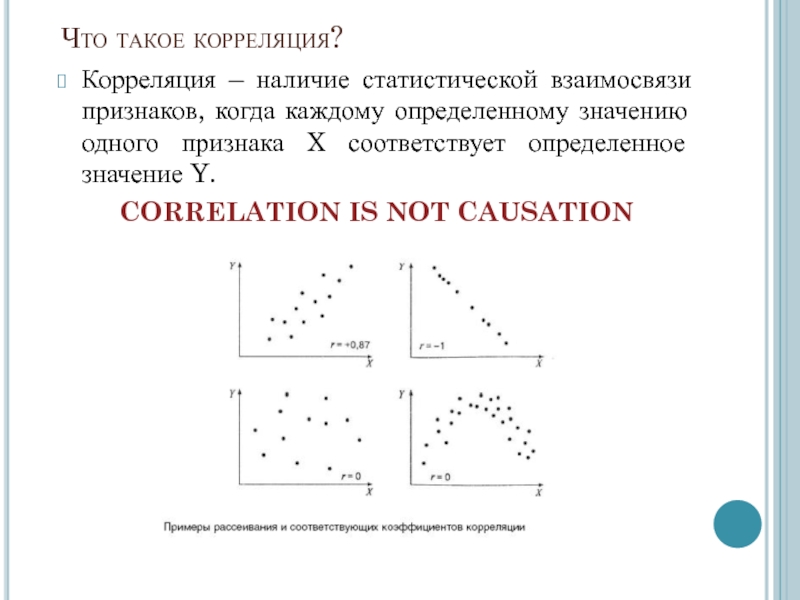
- 15. Что такое корреляция?Корреляция – наличие статистической взаимосвязи
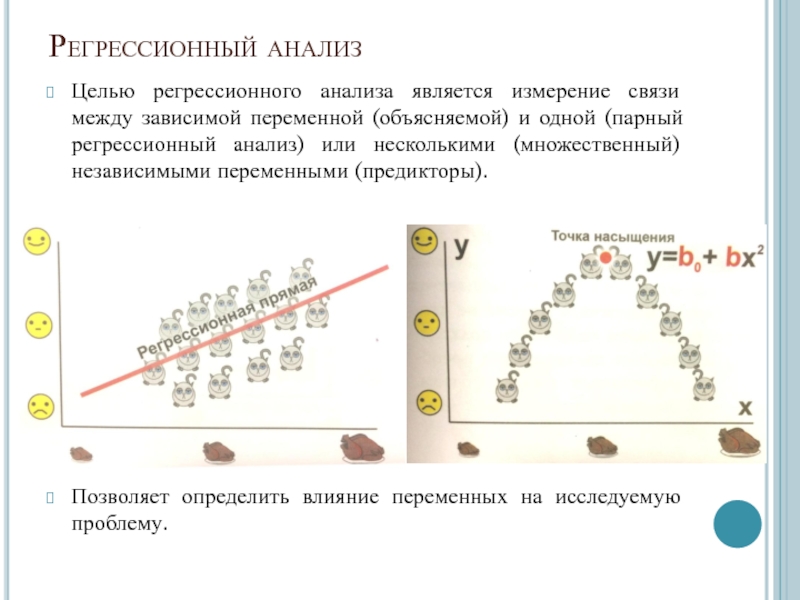
- 16. Регрессионный анализЦелью регрессионного анализа является измерение связи
- 17. Дискриминантный анализПозволяет определить критерии для отнесения объекта измерения к тому или иному классу.
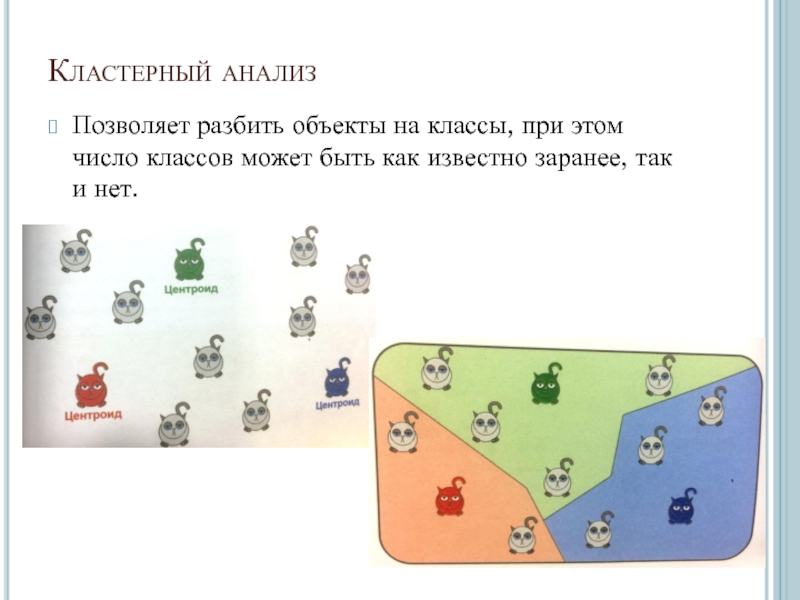
- 18. Кластерный анализПозволяет разбить объекты на классы, при
- 19. Факторный анализПозволяет сократить количество переменных, заменив их
- 20. Скачать презентанцию
Когда и зачем применяетсяПри наличии большого массива данных:Получение усредненных данныхОценка связей между переменнымиКлассификацияКластеризацияРедукция данных
Слайды и текст этой презентации
Слайд 2Когда и зачем применяется
При наличии большого массива данных:
Получение усредненных данных
Оценка
связей между переменными
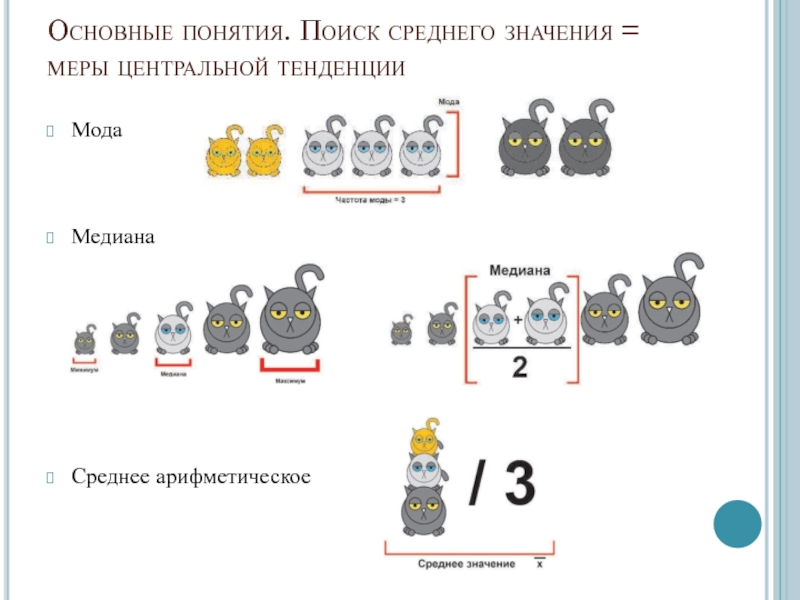
Слайд 4Основные понятия. Поиск среднего значения = меры центральной тенденции
Мода
Медиана
Среднее арифметическое
Слайд 5Выброс:
Квантиль – точка на числовой оси, делящая всю совокупность
упорядоченных измерений на две группы с известным соотношением их численности.
Процентили – это величины (99 точек), делящие выборку данных на сто групп, содержащих (по возможности) равное количество наблюдений
Квартили – 3 точки значения признака на числовой оси (P25, P50, P75), делящие множество на 4 части.
Слайд 6Меры изменчивости
Размах — разность между минимальным и максимальным значением: R
=Xmax – Xmin
Межквартильный размах: R = X75 –
X25Дисперсия – мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их среднеарифметического
Стандартное отклонение - квадратный корень из дисперсии
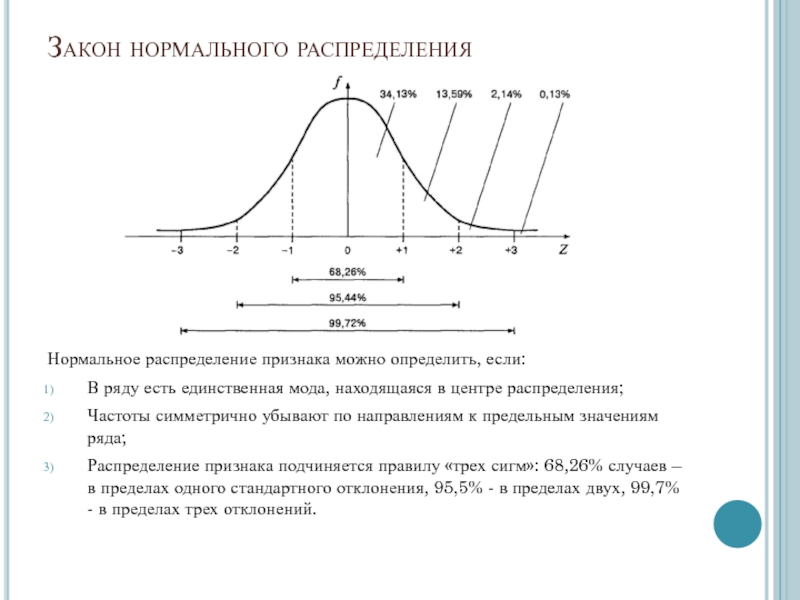
Слайд 8Закон нормального распределения
Нормальное распределение признака можно определить, если:
В ряду
есть единственная мода, находящаяся в центре распределения;
Частоты симметрично убывают по
направлениям к предельным значениям ряда; Распределение признака подчиняется правилу «трех сигм»: 68,26% случаев – в пределах одного стандартного отклонения, 95,5% - в пределах двух, 99,7% - в пределах трех отклонений.
Слайд 10Статистическая значимость
В гумманитарных науках устанавливается, как правило, на уровне
5% (p=0,05).
Применяется для сравнения нескольких выборок и означает, что вероятность
случайного появления обнаруженных различий составляет не более 5%.Чем меньше значение p/уровня, тем выше статистическая значимость результата исследования, подтверждающего гипотезу.
Слайд 11Χ-квадрат по Пирсону:
наличие связи между переменными
Критерий Хи-квадрат показывает, является ли
отклонение реально измеренных признаков от их вероятностного распределения случайным или
можно говорить о связи признаков.
Слайд 12Расчет Хи-квадрат
Находим теоретические (ожидаемые) частоты:
nтеор = итого по строке х
итого по столбцу
общее число наблюдений
Слайд 13далее – сравнение с табличным критическим значением с учетом «степени
свободы».
df = (r – 1)(c –
1)где r и с - количество категорий в колонке (column) и строке (row)
В примере: df = (3 – 1)(2 – 1) = 2
Слайд 15Что такое корреляция?
Корреляция – наличие статистической взаимосвязи признаков, когда каждому
определенному значению одного признака X соответствует определенное значение Y.
CORRELATION IS
NOT CAUSATION 
Слайд 16Регрессионный анализ
Целью регрессионного анализа является измерение связи между зависимой переменной
(объясняемой) и одной (парный регрессионный анализ) или несколькими (множественный) независимыми
переменными (предикторы).Позволяет определить влияние переменных на исследуемую проблему.
Слайд 17Дискриминантный анализ
Позволяет определить критерии для отнесения объекта измерения к тому
или иному классу.
Слайд 18Кластерный анализ
Позволяет разбить объекты на классы, при этом число классов
может быть как известно заранее, так и нет.
Слайд 19Факторный анализ
Позволяет сократить количество переменных, заменив их набором факторов. Может
являться предварительной процедурой перед регрессионным анализом, если ряд предикторов коррелируют
между собой.
