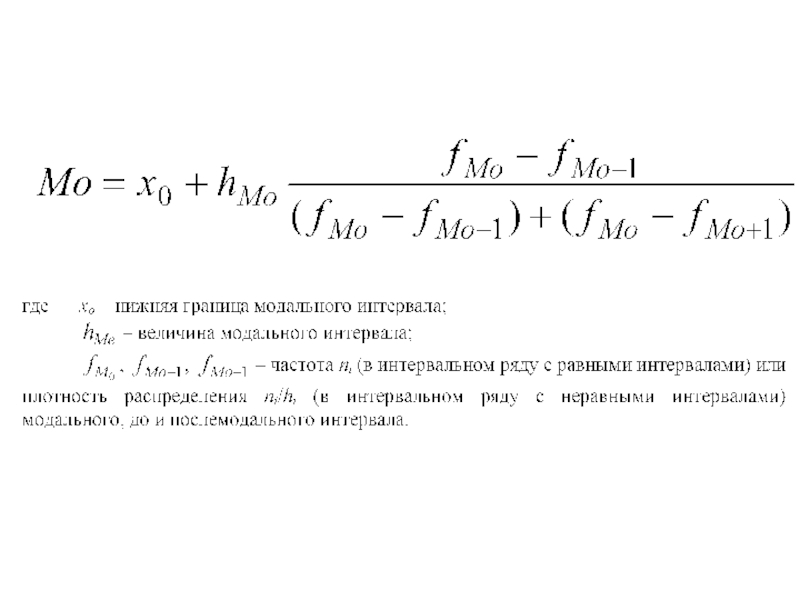Слайд 1Статистические величины
Лекция 3
Слайд 2Вопросы лекции:
Назначение и виды статистических величин.
Абсолютные величины, единицы измерения.
Относительные величины: понятие, правила расчета. Виды и взаимосвязи относительных величин:
относительные величины динамики, планового задания и выполнения плана, структуры, координации, сравнения, интенсивности.
Средние величины, общие принципы их применения. Виды средних величин, особенности исчисления. Степенные средние: средняя арифметическая, средняя геометрическая, средняя гармоническая. Выбор формы средних величин.
Слайд 31 Назначение и виды статистических величин. Абсолютные величины, единицы измерения
Под
статистическим показателем понимается количественная характеристика изучаемого объекта или его свойства.
На этапе статистической сводки от индивидуальных значений признаков совокупности путем суммирования переходят к показателям совокупности, которые называются обобщающими.
Слайд 4Система статистических показателей продукции промышленного предприятия включает следующие показатели:
товарная продукция;
отгруженная
продукция;
реализованная продукция;
чистая продукция;
добавленная стоимость и др.
!!!Раньше учитывали товарную продукцию, а
в новых условиях – чистую и добавленную стоимость.
Слайд 5Система экономико-статистических показателей в управлении предприятиями призвана выполнять четыре функции:
директивную
(плановые показатели, нормативы, разряды, ставка);
учетную (фактические результаты деятельности);
стимулирующую (зарплата, средняя
численность, развитие производства);
познавательную (сведения о налогах, трудоустройстройстве, среднем возрасте и т.д.).
Слайд 6
В зависимости от методов расчета обобщающие статистические показатели могут быть:
абсолютными;
относительными;
средними
величинами.
Слайд 72 Абсолютными
в статистике называются суммарные обобщающие показатели, характеризующие размеры, объемы,
уровни, мощности, темпы и др. изменения величин. Абсолютные показатели являются
именованными числами, т.е. измеримы.
Слайд 8Существуют:
натуральные, стоимостные и условно-натуральные (условное топливо, эталонные лошадиные силы) измерители.
Они служат для описания фактического состояния объекта, установления плановых и
прогнозных значений. Абсолютные показатели могут быть сравнимы в разные периоды времени (прошлый, настоящий, будущий).
Абсолютные показатели позволяют точно характеризовать объект в данный момент времени, но должны уточняться в динамике (сопоставимые цены, инвестиции с учетом инфляции и т.д.).
Слайд 93 Относительные статистические величины –
это показатели в виде коэффициентов,
характеризующих долю отдельных частей, изучаемой совокупности во всем ее объеме.
Относительные
показатели при исследовании экономических явлений и процессов изучаются совместно с абсолютными показателями и обеспечивают сопоставимость сравниваемой и базовой величин.
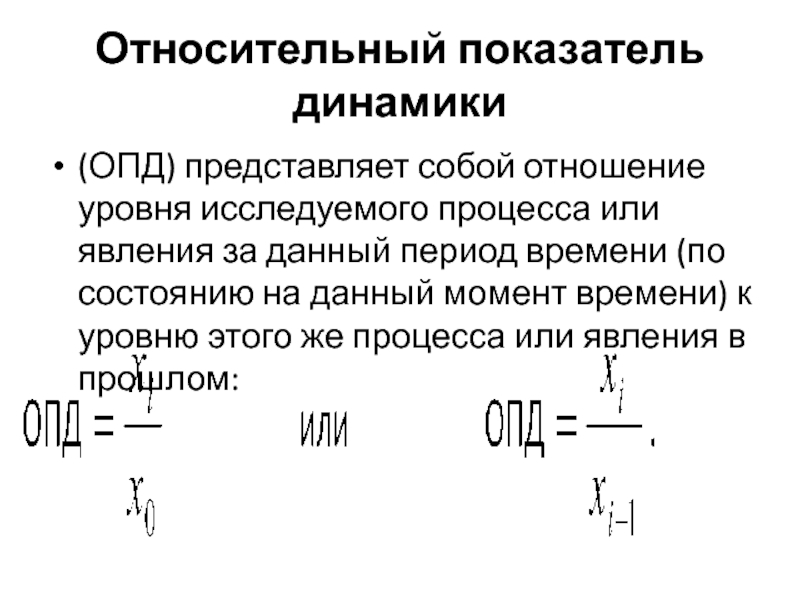
Слайд 10Относительный показатель динамики
(ОПД) представляет собой отношение уровня исследуемого процесса
или явления за данный период времени (по состоянию на данный
момент времени) к уровню этого же процесса или явления в прошлом:
Слайд 11Относительный показатель структуры
(ОПС) представляет собой отношение структурных частей изучаемого
объекта и их целого:
Выражается относительный показатель структуры в долях единицы
или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какой долей обладает или какой удельный вес имеет та или иная часть в общем итоге.
Слайд 12Относительный показатель координации
(ОПК) представляет собой отношение одной части совокупности
к другой части этой же совокупности:
Слайд 13При этом в качестве базы сравнения выбирается та часть, которая
имеет наибольший удельный вес или является приоритетной с экономической, социальной
или какой-либо другой точки зрения.
В результате получают величину, отражающую во сколько раз данная часть больше базисной или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда – на 100, 1000 и т.д. единиц) базисной структурной части.
Слайд 14Относительный показатель сравнения
(ОПСр) представляет собой отношение одноименных абсолютных показателей,
характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.):
Слайд 15Относительный показатель интенсивности
(ОПИ) характеризует степень распространения изучаемого процесса или
явления и представляет собой отношение исследуемого показателя к размеру присущей
ему среды:
где xA – показатель, характеризующий явление А;
YA – показатель, характеризующий среду распространения явления А.
Слайд 16Данный показатель получают сопоставлением уровней двух взаимосвязанных в своем развитии
явлений. Поэтому, наиболее часто он представляет собой именованную величину, но
может быть выражен и в процентах и т.п.
Обычно ОПИ рассчитывается в тех случаях, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения. Так, например, для определения уровня обеспеченности населения легковыми автомобилями рассчитывается число автомашин, приходящихся на 100 семей, для определения плотности населения рассчитывается число людей, приходящихся на 1 км2.
Слайд 17Относительные показатели уровня экономического развития
характеризующие производство продукции в расчете на
душу населения и играющие важную роль в оценке развития экономики
государства. Так как объемные показатели производства продукции по своей природе являются интервальными, а показатель численности населения – моментным, в расчетах используют среднюю за период численность населения.
Слайд 18Относительные показатели плана и реализации плана
используются для целей планирования
и сравнения реально достигнутых результатов с ранее намеченными.
Слайд 19где ОПП – относительный показатель плана;
Х пл i+1 – уровень, планируемый
на i+1 период;
xi – уровень, достигнутый в i-м периоде.
где ОПРП –
относительный показатель реализации плана;
xi – уровень, достигнутый в (i+1)-м периоде.
Слайд 20ОПП характеризует
напряженность плана, т.е. во сколько раз намечаемый объем производства
превысит достигнутый уровень или сколько процентов от этого уровня составит.
ОПРП отражает фактический объем производства в процентах или коэффициентах по сравнению с плановым уровнем.
Слайд 21Относительные величины
выполнения плана и динамики связаны между собой следующими
соотношениями:
Слайд 224 Средняя величина
является обобщающей характеристикой совокупности однотипных явлений по
изучаемому признаку. Средняя величина должна вычисляться с учетом экономического содержания
определяемого показателя.
Слайд 24Все виды средних делятся на:
степенные (аналитические, порядковые) средние (арифметическая, гармоническая,
геометрическая, квадратическая);
структурные (позиционные) средние (мода и медиана) – применяются для
изучения структуры рядов распределения.
Слайд 25Средние степенные величины
Средняя степенная (при различной величине k) определяется
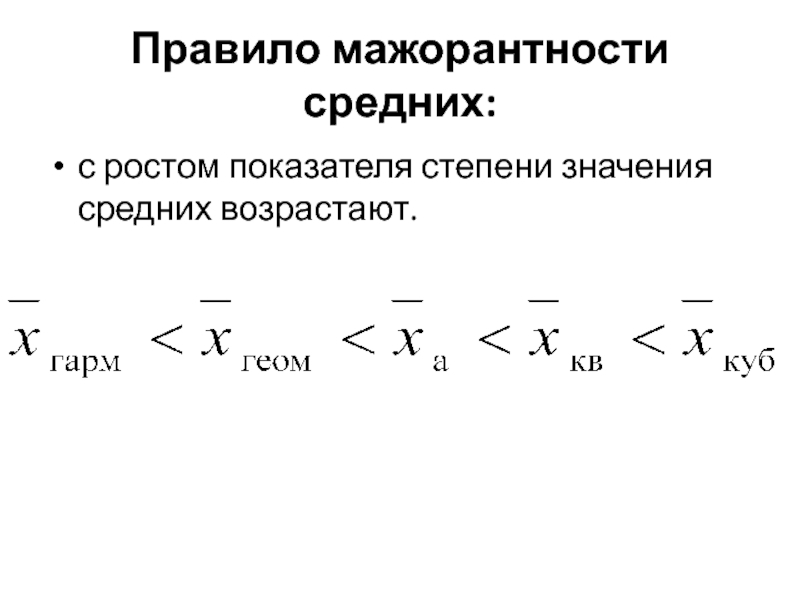
Слайд 28Правило мажорантности средних:
с ростом показателя степени значения средних возрастают.
Слайд 29Средние структурные величины
В условиях недостаточности средних используют структурные средние величины
– моду и медиану.
Медиана (Ме) – это вариант, который находится
в середине вариационного ряда. Медиана делит ряд на две равные (по числу наблюдений) части. В ранжированных рядах не сгруппированных данных нахождение медианы сводится к отысканию порядкового номера и значения варианта у этого номера.
Слайд 30Котики бывают разные. Есть большие котики, а есть маленькие. Есть котики
с длинными хвостами, а есть и вовсе без хвостов. Есть котики с висячими ушками,
а есть котики с короткими лапками. Как же нам понять, как выглядит типичный котик?
Слайд 32мы можем упорядочить всех котиков от самого маленького до самого крупного, а затем
посмотреть на середину этого ряда. Как правило, там находится котик, который
обладает самым типичным размером. И этот размер называется медианой
Слайд 34Если же посередине находятся сразу два котика (что бывает, когда их
четное количество), то чтобы найти медиану, нужно сложить их размеры
и поделить это число пополам.
Слайд 35
Медиана в интервальных вариационных рядах рассчитывается по формуле:
Слайд 36где х0 – нижняя граница медианного интервала (накопленная частота которого
превышает половину общей суммы частот);
h Me – величина медианного интервала;
S
Me-1 – накопленная частота интервала, предшествующего медианному;
n Me– частота медианного интервала.
Слайд 37Главное свойство медианы заключается в том, что сумма абсолютных отклонений
значений признака от медианы меньше, чем от любой другой величины:
Слайд 38Модой (Мо)
вариационного ряда называется вариант, которому соответствует наибольшая частота.
Для вычисления моды в интервальном ряду сначала находится модальный интервал,
имеющий наибольшую частоту (или наибольшую плотность распределения – отношение частоты интервала к его величине ni/hi – в интервальном ряду с неравными интервалами), а значение моды определяется линейной интерполяцией:
Слайд 40Для простоты мы возьмем такое котиковое свойство, как размер.
Первый и наиболее
очевидный способ – посмотреть, какой размер котиков встречается чаще всего. Такой
показатель называется модой.
Слайд 42Мода так же, как и медиана обладает определенной устойчивостью к
вариации признака. Если в совокупности первичных признаков нет повторяющихся значений,
то для определения моды проводят группировку.