Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СТРОИТЕЛЬНАЯ МЕХАНИКА
Содержание
- 1. СТРОИТЕЛЬНАЯ МЕХАНИКА
- 2. Строительная механика стержневых системВ курсе "Сопротивление материалов"
- 3. 1. ИДЕЯ И ОСНОВНЫЕ ПОЛОЖЕНИЯ МЕТОДА ПЕРЕМЕЩЕНИЙВ
- 4. Чтобы рассчитать раму, достаточно предварительно решить вспомогательную
- 5. Рассмотрим чуть более сложную задачу. Теперь на
- 6. Запретим поворот узла рамы, поставив заделку. Эту
- 7. Реакцию дополнительной связи будем считать положительной, если
- 8. Составим выражение для полного реактивного момента в
- 9. Ниже рассматривается более сложная для расчета рама,
- 10. Чтобы составить канонические уравнения метода перемещений, последовательно
- 11. Реакции при действии внешних сил обозначаются k1F,
- 12. Таким образом, для формирования уравнений метода перемещений
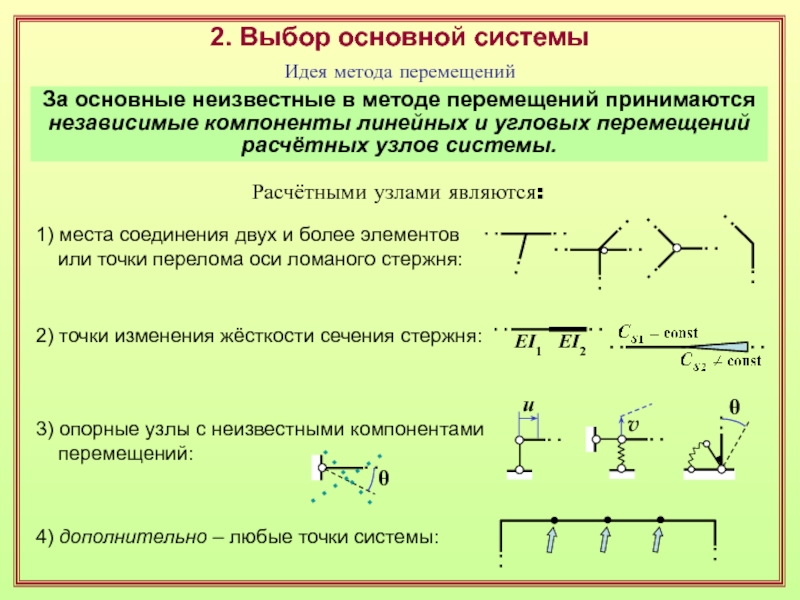
- 13. 2. Выбор основной системыИдея метода перемещенийЗа основные
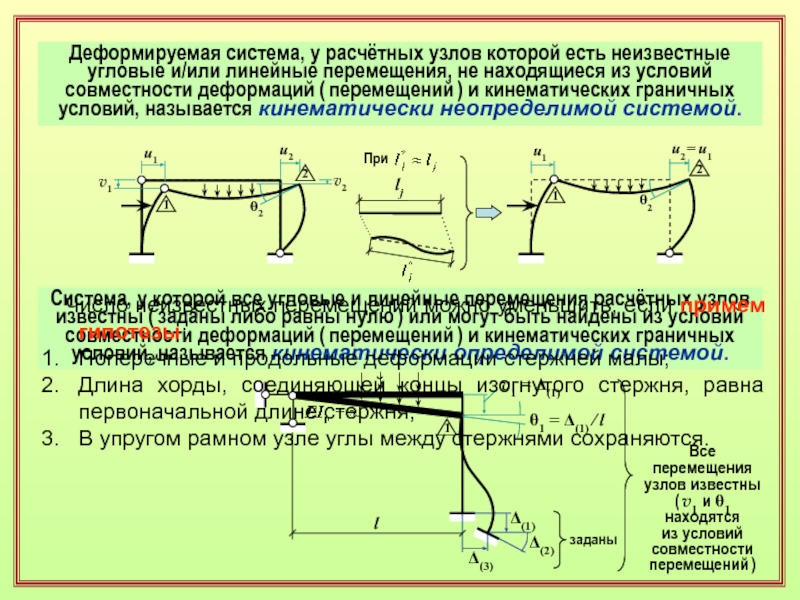
- 14. Деформируемая система, у расчётных узлов которой есть
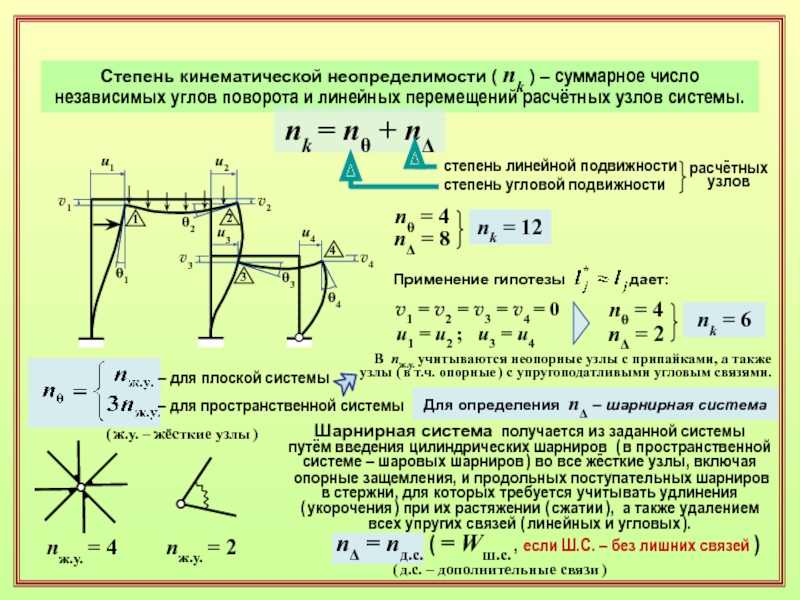
- 15. Степень кинематической неопределимости ( nk ) –
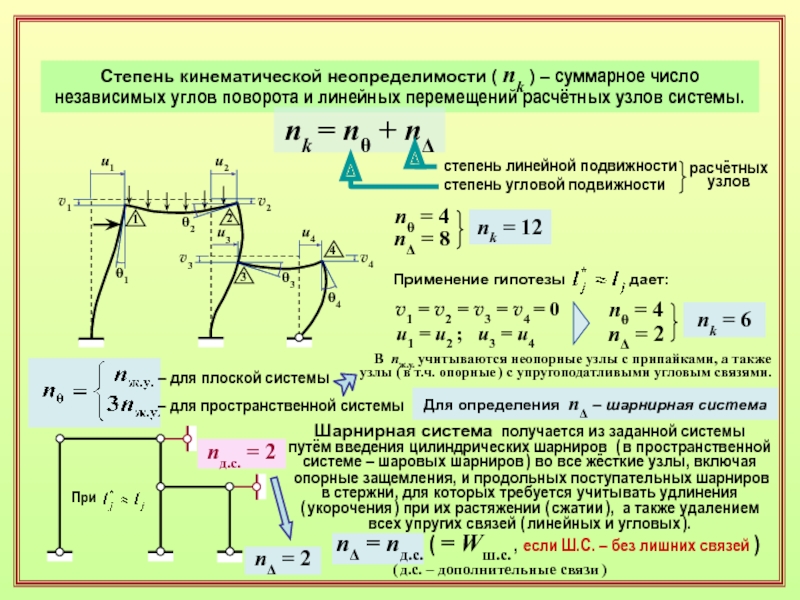
- 16. Степень кинематической неопределимости ( nk ) –
- 17. Степень кинематической неопределимости ( nk ) –
- 18. Основная система метода перемещений– это, как правило,
- 19. Для получения основной системы МП
- 20. Тогда в рассмотренной раме достаточно
- 21. Из 3-ей гипотезы (о том
- 22. Общее число всех неизвестных определяется
- 23. Для получения ОС метода перемещений
- 24. 3. МАТРИЦА ЖЕСТКОСТИ ТИПОВОГО ЭЛЕМЕНТАТиповым элементом рассмотренных
- 25. Используя дифференциальные соотношения для упругой линии балки:-кривизна
- 26. Найдем неизвестные реакции r11 и r21, исходя
- 27. Второй вид деформации балки. Левому торцу балки
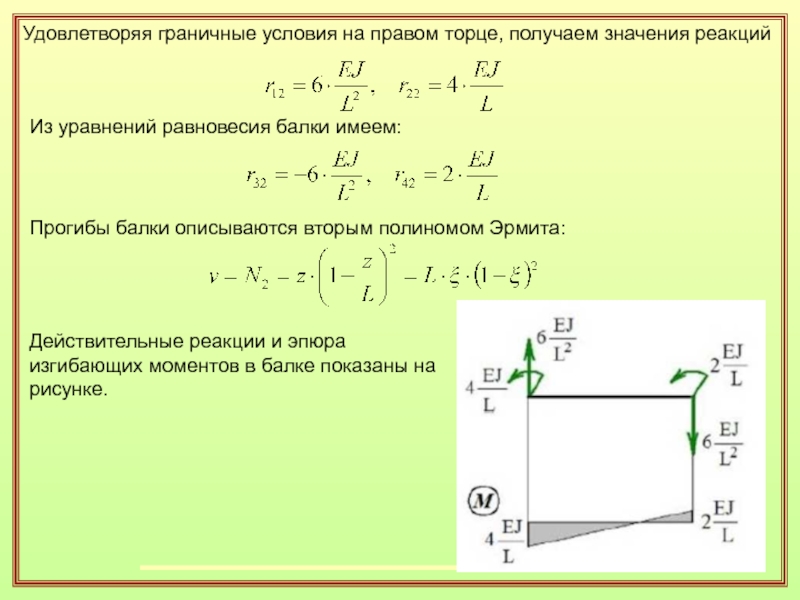
- 28. Удовлетворяя граничные условия на правом торце, получаем
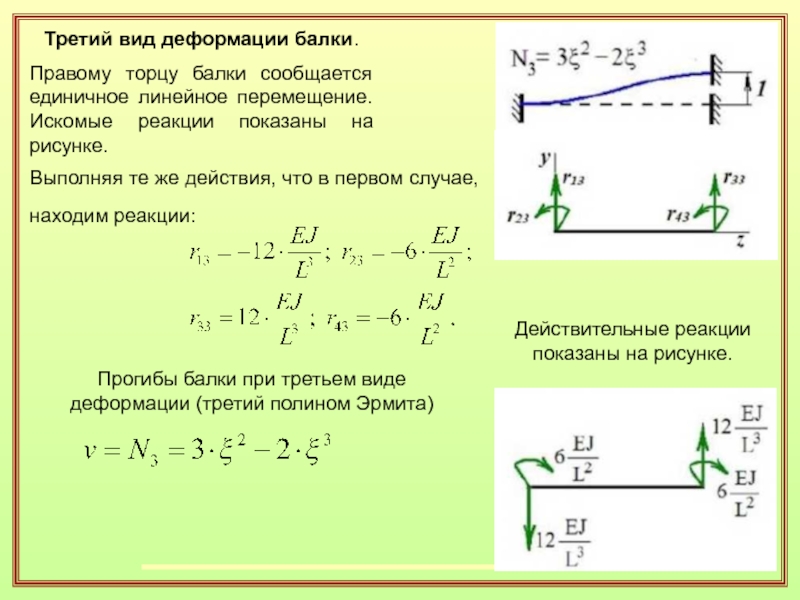
- 29. Третий вид деформации балки. Правому торцу балки
- 30. Четвертый вид деформации балки. Правому торцу балки
- 31. Реакции, найденные для всех четырех видов деформации
- 32. 4. РЕАКЦИИ СВЯЗЕЙ ОТ ЗАДАННЫХ ВНЕШНИХ СИЛОпределим
- 33. Состояние балки при действии внешней силы будем
- 34. Полученный результат позволяет сформулировать общее правило определения
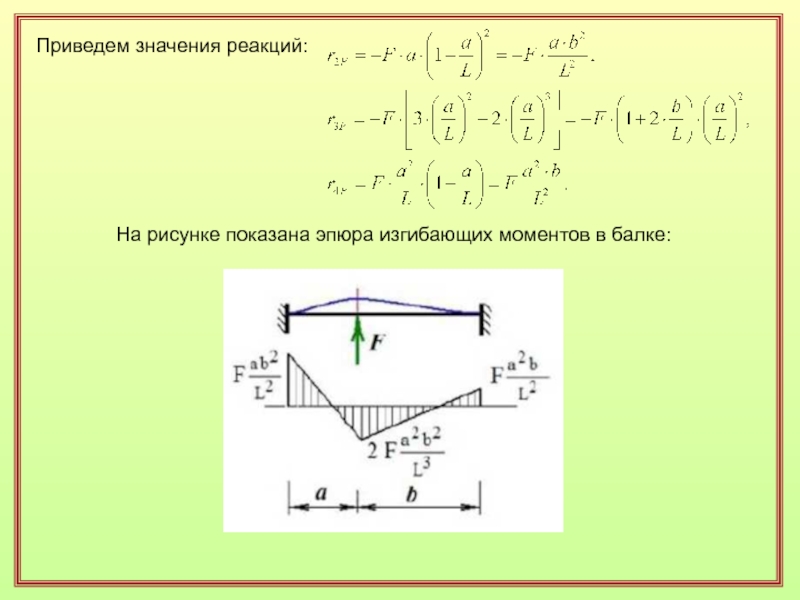
- 35. Приведем значения реакций:На рисунке показана эпюра изгибающих моментов в балке:
- 36. Если сила F приложена посредине балки, то
- 37. Рассмотрим определение реакций в заделках при произвольной
- 38. Найдем реакции при действии равномерно распределенной нагрузки,
- 39. Типовые элементы плоской основной системы метода перемещенийEIj
- 40. Тип 1qljТип 2б) о т н
- 41. Таким образом Получены жесткости типового элемента
- 42. Сравним метод сил (МС) и метод перемещений
- 43. ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙРассчитаем раму, изображенную
- 44. Далее рассмотрим состояние основной системы при единичном
- 45. Суммарная эпюра изгибающих моментов представлена на рисунке.
- 46. ЗАКЛЮЧИТЕЛЬНОЕ ЗАМЕЧАНИЕИдея расчета конструкций с использованием перемещений
- 47. Из множества конечных элементов собирается расчетная модель
- 48. К о н т р о л
- 49. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1СТРОИТЕЛЬНАЯ
МЕХАНИКА
Строительная механика стержней
Метод сил
Метод перемещений
Доцент кафедры
«Самолетостроение»
к.т.н. Мухин
Д.В.
Слайд 2Строительная механика стержневых систем
В курсе "Сопротивление материалов" традиционно излагается метод
сил как универсальный способ расчета статически неопределимых стержневых систем. Признавая
важность изучения метода сил в формировании представлений будущего инженера о расчетах конструкций на прочность, необходимо учитывать, что в современной расчетной практике доминирует альтернативный подход, называемый методом перемещений. Именно метод перемещений стал историческим предшественником наиболее мощного современного метода анализа напряженного состояния конструкций - метода конечных элементов (МКЭ). Применению МКЭ способствует широкое распространение индустриальных программных комплексов, реализующих этот метод.Изучение расчета рам с использованием метода перемещений является ключевым для дальнейшего понимания идей МКЭ и подготовки к его применению. В данном курсе изложение метода перемещений ограничено задачей изгиба плоских рам, однако, при необходимости технику применения этого метода, весьма легко распространить знания на другие задачи расчета стержневых систем. Плоские рамы являются наиболее подходящим объектом для иллюстрации идей метода перемещений, поскольку в случае сложных рамных конструкций преимущества метода становятся особенно очевидными.
Слайд 31. ИДЕЯ И ОСНОВНЫЕ ПОЛОЖЕНИЯ МЕТОДА ПЕРЕМЕЩЕНИЙ
В методе сил в
качестве основных неизвестных, через которые выражаются все искомые величины, принимают
или реакции связей, или внутренние силы X в некоторых сечениях конструкции. Для расчета сложных (много раз статически неопределимых) систем разработан альтернативный подход, называемый методом перемещений. В методе перемещений за основные неизвестные принимают перемещения характерных сечений или узлов конструкции. Эти перемещения выбирают так, чтобы через них можно было выразить все искомые величины: деформации, внутренние силы, напряжения во всем объеме конструкции.Рассмотрим идею и технику метода перемещений на примере расчета плоских рам. Так же, как в методе сил, будем пренебрегать изменением длин стержней, считая их нерастяжимыми. Рассмотрим простейший пример:
Деформированное состояние рамы определяетcя одним углом поворота Z1. Если угол поворота Z1 определен, то известны прогибы стержней и, следовательно, внутренние силы.
M
Z1
Z1
Z1
Слайд 4Чтобы рассчитать раму, достаточно предварительно решить вспомогательную задачу о деформациях
балки при принудительном повороте торцевого сечения на угол, равный единице.
Момент, необходимый дня созданияединичного угла поворота торца, обозначим k11. В дальнейшем коэффициент k11, значение которого зависит от параметров балки, будем называть жесткостью балки при перемещении по направлению 1.
Используя свойство линейности упругой системы, запишем очевидное уравнение, выражающее равенство общего приложенного момента сумме моментов, действующих на каждую балку:
Здесь верхний индекс коэффициентов k11 указывает номер балки.
Из данного уравнения определяется угол поворота Z1 и далее все силовые факторы, прогибы и напряжения.
Рассмотренный пример особенно прост потому, что нагрузка приложена к узлу рамы.
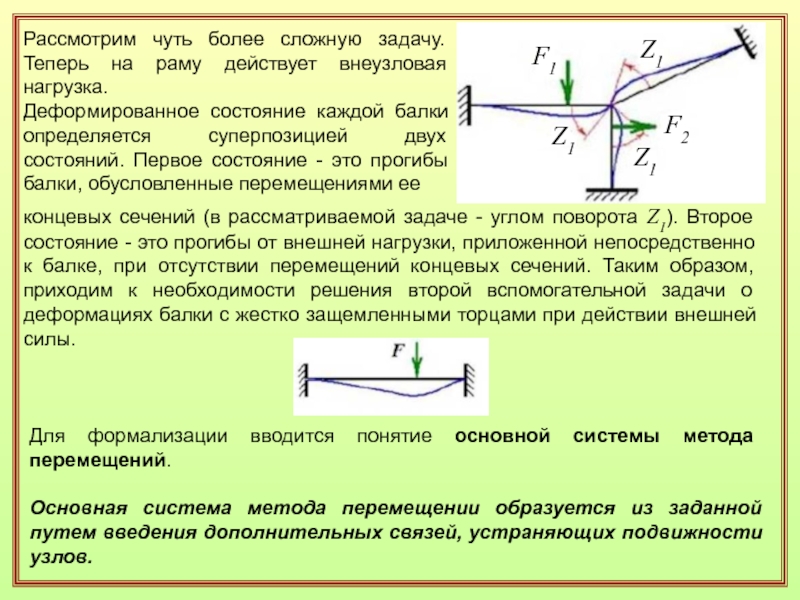
Слайд 5Рассмотрим чуть более сложную задачу. Теперь на раму действует внеузловая
нагрузка.
Деформированное состояние каждой балки определяется суперпозицией двух состояний. Первое
состояние - это прогибы балки, обусловленные перемещениями ееконцевых сечений (в рассматриваемой задаче - углом поворота Z1). Второе состояние - это прогибы от внешней нагрузки, приложенной непосредственно к балке, при отсутствии перемещений концевых сечений. Таким образом, приходим к необходимости решения второй вспомогательной задачи о деформациях балки с жестко защемленными торцами при действии внешней силы.
Для формализации вводится понятие основной системы метода перемещений.
Основная система метода перемещении образуется из заданной путем введения дополнительных связей, устраняющих подвижности узлов.
F2
F1
Z1
Z1
Z1
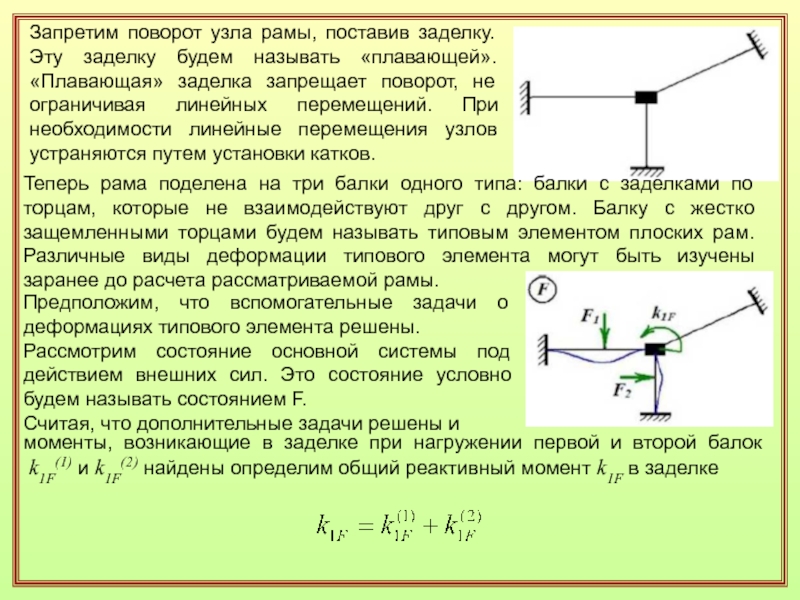
Слайд 6Запретим поворот узла рамы, поставив заделку. Эту заделку будем называть
«плавающей». «Плавающая» заделка запрещает поворот, не ограничивая линейных перемещений. При
необходимости линейные перемещения узлов устраняются путем установки катков.Теперь рама поделена на три балки одного типа: балки с заделками по торцам, которые не взаимодействуют друг с другом. Балку с жестко защемленными торцами будем называть типовым элементом плоских рам. Различные виды деформации типового элемента могут быть изучены заранее до расчета рассматриваемой рамы.
Предположим, что вспомогательные задачи о деформациях типового элемента решены.
Рассмотрим состояние основной системы под действием внешних сил. Это состояние условно будем называть состоянием F.
Считая, что дополнительные задачи решены и
моменты, возникающие в заделке при нагружении первой и второй балок
k1F(1) и k1F(2) найдены определим общий реактивный момент k1F в заделке
Слайд 7Реакцию дополнительной связи будем считать положительной, если ее направление совпадает
с направлением положительного перемещения. Таким образом, положительные направления узловых перемещений
и узловых реакций согласованы. Очевидно, что для рассматриваемой рамы k1F<0.Далее рассмотрим состояние основной системы при повороте плавающей заделки на угол, равный единице. Это состояние назовем 1.
Вычислим реактивный момент в заделке или, что то же самое, момент, приложенный к узлу для
получения единичного угла поворота. Этот момент определяется сложением моментов для отдельных балок:
В линейно-упругих системах внутренние силы и реакции связей пропорциональны перемещениям (закон Гука во внешних факторах и перемещениях), поэтому при угле поворота u1 момент будет равен k11∙Z1.
Слайд 8Составим выражение для полного реактивного момента в дополнительной заделке, складывая
его значения в двух рассмотренных состояниях. Полный реактивный момент равен
нулю, так как в действительности дополнительная связь отсутствует:Полученное уравнение называется каноническим уравнением метода перемещений. Еще раз подчеркнем, что смысл этого уравнения отсутствие реакции дополнительной связи. Иначе говоря, это условие равновесия моментов в узле рамы, выраженное через перемещение.
Из полученного уравнения определяется угол поворота Z1, а далее все внутренние силовые факторы в раме.
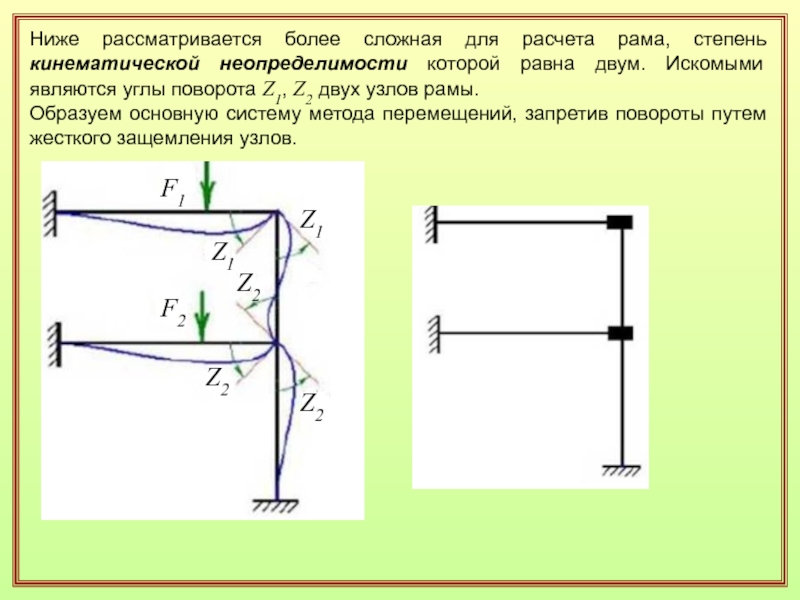
Слайд 9Ниже рассматривается более сложная для расчета рама, степень кинематической неопределимости
которой равна двум. Искомыми являются углы поворота Z1, Z2 двух
узлов рамы.Образуем основную систему метода перемещений, запретив повороты путем жесткого защемления узлов.
F2
F1
Z1
Z1
Z2
Z2
Z2
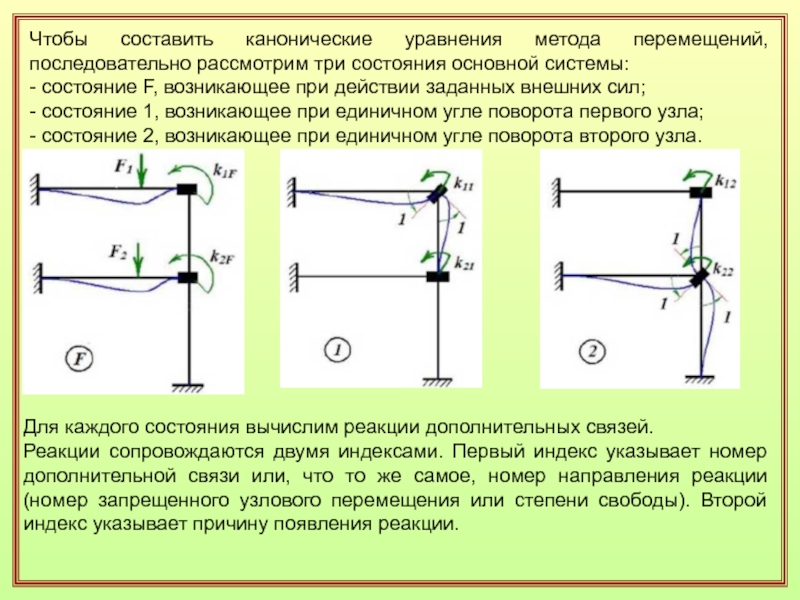
Слайд 10Чтобы составить канонические уравнения метода перемещений, последовательно рассмотрим три состояния
основной системы:
- состояние F, возникающее при действии заданных внешних сил;
-
состояние 1, возникающее при единичном угле поворота первого узла;- состояние 2, возникающее при единичном угле поворота второго узла.
Для каждого состояния вычислим реакции дополнительных связей.
Реакции сопровождаются двумя индексами. Первый индекс указывает номер дополнительной связи или, что то же самое, номер направления реакции (номер запрещенного узлового перемещения или степени свободы). Второй индекс указывает причину появления реакции.
Слайд 11Реакции при действии внешних сил обозначаются k1F, k2F и т.д.
Реакции при единичных перемещениях узлов обозначаются
kij, где индекс j указывает направление единичного перемещения. Таким образом, kij - реакция i-й связи (в направлении i) при единичном перемещении j-й связи (в направлении j). Реакции kij называются коэффициентами жесткости конструкции. Подчеркнем, что конкретное определение реакций kiF, kij основано на предварительном решении ряда вспомогательных задач для типового элемента рам, которые будут рассмотрены ниже.Используя принцип суперпозиции, составим выражения для истинных значений реакций дополнительных связей:
Канонические уравнения метода перемещений целесообразно записывать в матричной форме:
где [K]=[kij] - квадратная матрица жесткости конструкции, {Z}={Zj} - матрица-столбец (вектор) искомых узловых перемещений, {KF}={kiF} матрица-столбец реакций от внешних сил. Из этой системы определяются перемещения узлов конструкции.
Слайд 12Таким образом, для формирования уравнений метода перемещений необходимо:
Определить количество возможных
направлений перемещений (степень кинематической неопределимости);
Получить матрицу жесткости для балки с
заделками по торцам;Определить реакции в заделках при действии внешних сил.
В последующих вопросах рассмотрим решение этих задач.
Слайд 132. Выбор основной системы
Идея метода перемещений
За основные неизвестные в методе
перемещений принимаются
независимые компоненты линейных и угловых перемещений
расчётных узлов системы.
Расчётными узлами являются:
1) места соединения двух и более элементов
или точки перелома оси ломаного стержня:
2) точки изменения жёсткости сечения стержня:
3) опорные узлы с неизвестными компонентами
перемещений:
4) дополнительно – любые точки системы:
EI1
EI2
u
v
q
q
Слайд 14Деформируемая система, у расчётных узлов которой есть неизвестные угловые и/или
линейные перемещения, не находящиеся из условий совместности деформаций ( перемещений
) и кинематических граничныхусловий, называется кинематически неопределимой системой.
Система, у которой все угловые и линейные перемещения расчётных узлов известны ( заданы либо равны нулю ) или могут быть найдены из условий совместности деформаций ( перемещений ) и кинематических граничных условий, называется кинематически определимой системой.
1
2
u1
u2
v1
v2
q2
1
2
u1
u2 = u1
q2
lj
При
D(1)
D(2)
D(3)
заданы
1
v1 = D(1)
l
q1 = D(1) / l
Все перемещения
узлов известны
( v1 и q1 находятся
из условий совместности перемещений )
Число неизвестных перемещений можно уменьшить, если примем гипотезы:
Поперечные и продольные деформации стержней малы;
Длина хорды, соединяющей концы изогнутого стержня, равна первоначальной длине стержня;
В упругом рамном узле углы между стержнями сохраняются.
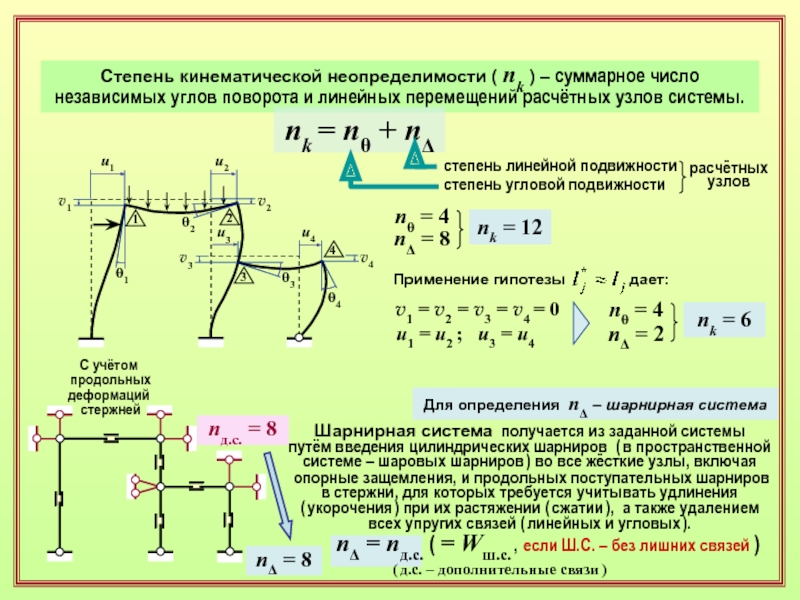
Слайд 15Степень кинематической неопределимости ( nk ) – суммарное число
независимых углов
поворота и линейных перемещений расчётных узлов системы.
nk = nq
+ nDстепень линейной подвижности
степень угловой подвижности
расчётных
узлов
1
2
3
4
u1
v1
q2
q1
q3
u2
v2
u3
v3
v4
u4
q4
nq = 4
nD = 8
nk = 12
Применение гипотезы дает:
v1 = v2 = v3 = v4 = 0
u1 = u2 ; u3 = u4
nq = 4
nD = 2
nk = 6
– для плоской системы
– для пространственной системы
nж.у. = 4
Для определения nD – шарнирная система
nж.у. = 2
nD = nд.c. ( = Wш.с. , если Ш.С. – без лишних связей )
В nж.у. учитываются неопорные узлы с припайками, а также
узлы ( в т.ч. опорные ) с упругоподатливыми угловым связями.
Шарнирная система получается из заданной системы
путём введения цилиндрических шарниров ( в пространственной системе – шаровых шарниров ) во все жёсткие узлы, включая
опорные защемления, и продольных поступательных шарниров в стержни, для которых требуется учитывать удлинения
( укорочения ) при их растяжении ( сжатии ), а также удалением всех упругих связей ( линейных и угловых ).
( ж.у. – жёсткие узлы )
( д.с. – дополнительные связи )
Слайд 16Степень кинематической неопределимости ( nk ) – суммарное число
независимых углов
поворота и линейных перемещений расчётных узлов системы.
nk = nq
+ nDстепень линейной подвижности
степень угловой подвижности
расчётных
узлов
1
2
3
4
u1
v1
q2
q1
q3
u2
v2
u3
v3
v4
u4
q4
nq = 4
nD = 8
nk = 12
Применение гипотезы дает:
v1 = v2 = v3 = v4 = 0
u1 = u2 ; u3 = u4
nq = 4
nD = 2
nk = 6
– для плоской системы
– для пространственной системы
Для определения nD – шарнирная система
При
nD = 2
nд.с. = 2
Шарнирная система получается из заданной системы
путём введения цилиндрических шарниров ( в пространственной системе – шаровых шарниров ) во все жёсткие узлы, включая
опорные защемления, и продольных поступательных шарниров в стержни, для которых требуется учитывать удлинения
( укорочения ) при их растяжении ( сжатии ), а также удалением всех упругих связей ( линейных и угловых ).
В nж.у. учитываются неопорные узлы с припайками, а также
узлы ( в т.ч. опорные ) с упругоподатливыми угловым связями.
nD = nд.c. ( = Wш.с. , если Ш.С. – без лишних связей )
( д.с. – дополнительные связи )
Слайд 17Степень кинематической неопределимости ( nk ) – суммарное число
независимых углов
поворота и линейных перемещений расчётных узлов системы.
nk = nq
+ nDстепень линейной подвижности
степень угловой подвижности
расчётных
узлов
1
2
3
4
u1
v1
q2
q1
q3
u2
v2
u3
v3
v4
u4
q4
nq = 4
nD = 8
nk = 12
Применение гипотезы дает:
v1 = v2 = v3 = v4 = 0
u1 = u2 ; u3 = u4
nq = 4
nD = 2
nk = 6
Для определения nD – шарнирная система
nD = 8
nд.с. = 8
=
=
=
=
=
=
С учётом
продольных
деформаций
стержней
Шарнирная система получается из заданной системы
путём введения цилиндрических шарниров ( в пространственной системе – шаровых шарниров ) во все жёсткие узлы, включая
опорные защемления, и продольных поступательных шарниров в стержни, для которых требуется учитывать удлинения
( укорочения ) при их растяжении ( сжатии ), а также удалением всех упругих связей ( линейных и угловых ).
nD = nд.c. ( = Wш.с. , если Ш.С. – без лишних связей )
( д.с. – дополнительные связи )
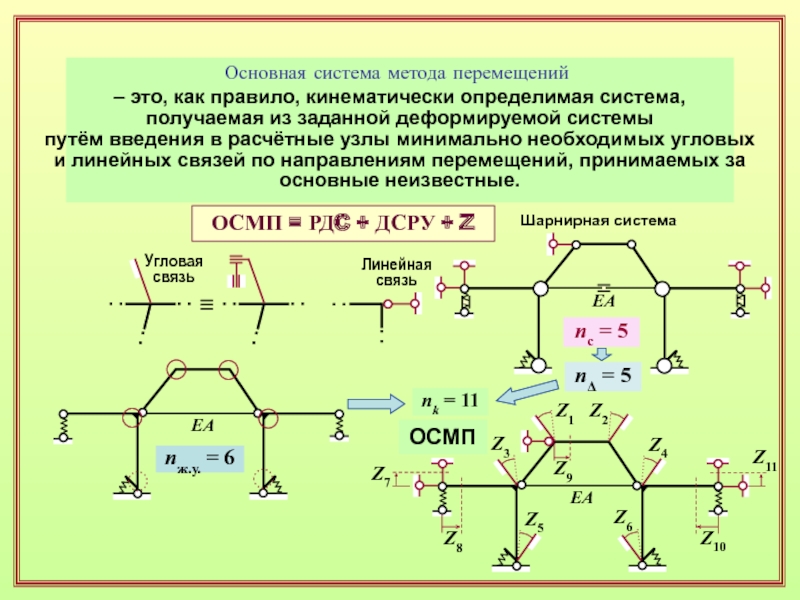
Слайд 18Основная система метода перемещений
– это, как правило, кинематически определимая система,
получаемая из заданной деформируемой системы
путём введения в расчётные узлы
минимально необходимых угловых и линейных связей по направлениям перемещений, принимаемых за основные неизвестные.Угловая
связь
Линейная
связь
EA
nж.у. = 6
EA
Шарнирная система
nD = 5
nс = 5
ОСМП
EA
Z1
Z2
Z3
Z4
Z5
Z6
Z7
Z8
Z9
Z10
Z11
nk = 11
ОСМП = РДC + ДСРУ + Z
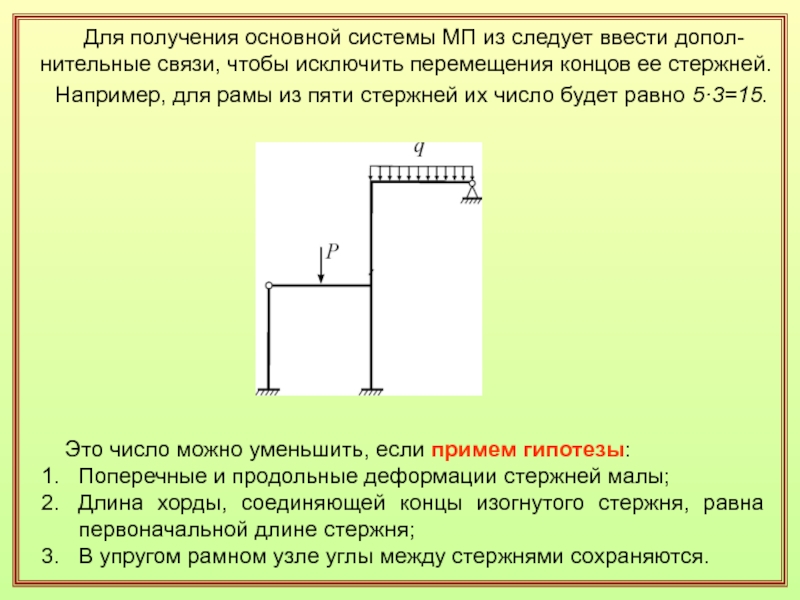
Слайд 19 Для получения основной системы МП из следует ввести
допол-нительные связи, чтобы исключить перемещения концов ее стержней.
Например, для рамы из пяти стержней их число будет равно 5·3=15. Это число можно уменьшить, если примем гипотезы:
Поперечные и продольные деформации стержней малы;
Длина хорды, соединяющей концы изогнутого стержня, равна первоначальной длине стержня;
В упругом рамном узле углы между стержнями сохраняются.
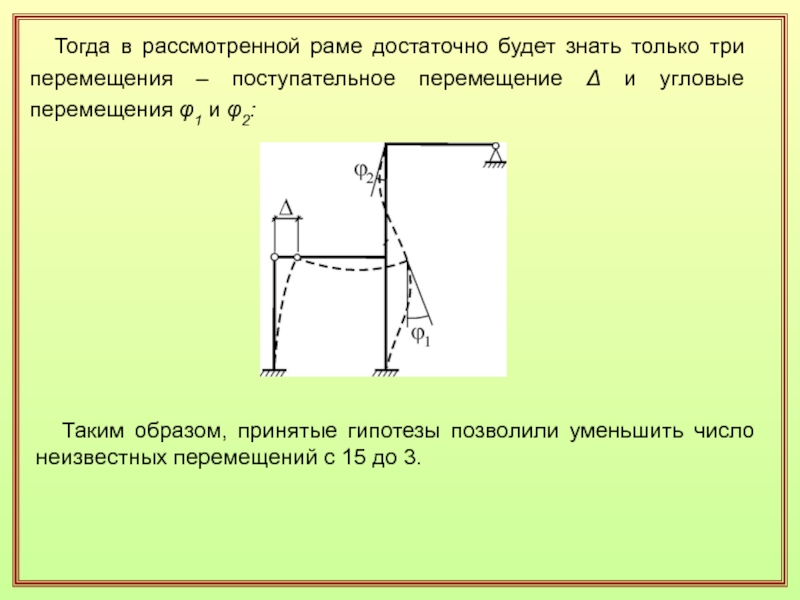
Слайд 20 Тогда в рассмотренной раме достаточно будет знать только
три перемещения – поступательное перемещение Δ и угловые перемещения φ1
и φ2: Таким образом, принятые гипотезы позволили уменьшить число неизвестных перемещений с 15 до 3.
Слайд 21 Из 3-ей гипотезы (о том что углы между
стержнями в упругом рамном узле сохраняются) следует, что число неизвестных
угловых перемещений будет определяться по формуле:nугл = числу упругих рамных узлов.
Для определения числа неизвестных поступательных (линейных) перемещений во все узлы рамы, включая и опоры, нужно ввести шарниры:
Например, в рассматриваемой раме nлин=2 6 – 5 – 6 =1.
Тогда число линейных перемещений можно определить по известной формуле кинематического анализа для фермы:
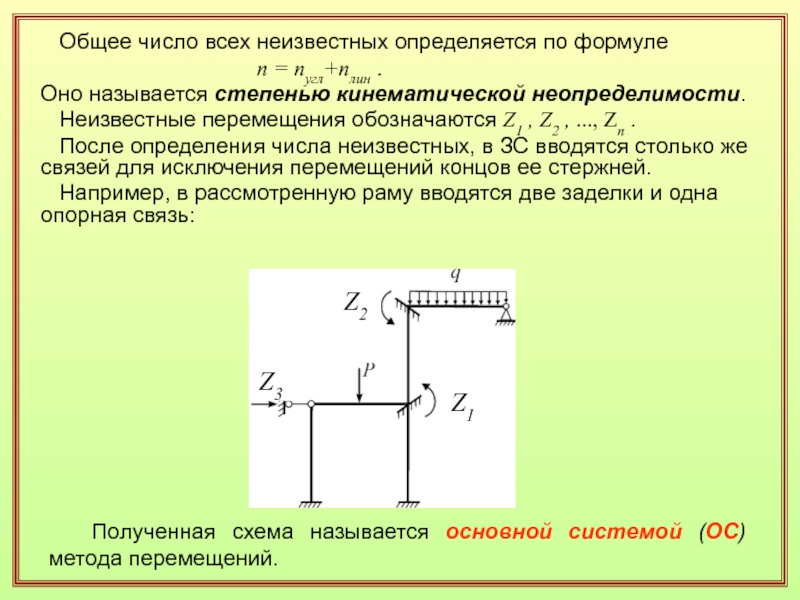
Слайд 22 Общее число всех неизвестных определяется по формуле
n
= nугл+nлин .Оно называется степенью кинематической неопределимости.
Неизвестные перемещения обозначаются Z1 , Z2 , ..., Zn .
После определения числа неизвестных, в ЗС вводятся столько же связей для исключения перемещений концов ее стержней.
Например, в рассмотренную раму вводятся две заделки и одна опорная связь:
Полученная схема называется основной системой (ОС) метода перемещений.
Z1
Z2
Z3
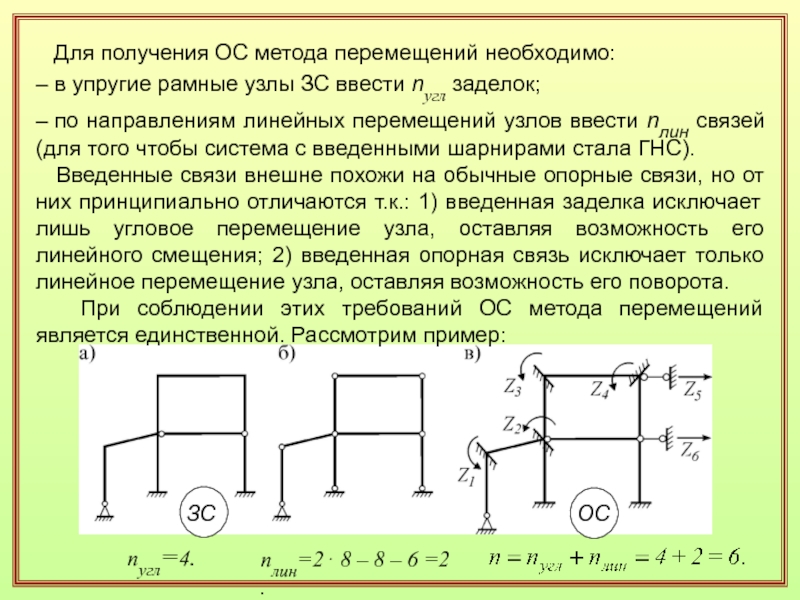
Слайд 23 Для получения ОС метода перемещений необходимо:
– в упругие рамные
узлы ЗС ввести nугл заделок;
– по направлениям линейных перемещений узлов ввести
nлин связей (для того чтобы система с введенными шарнирами стала ГНС).Введенные связи внешне похожи на обычные опорные связи, но от них принципиально отличаются т.к.: 1) введенная заделка исключает лишь угловое перемещение узла, оставляя возможность его линейного смещения; 2) введенная опорная связь исключает только линейное перемещение узла, оставляя возможность его поворота.
При соблюдении этих требований ОС метода перемещений является единственной. Рассмотрим пример:
nугл=4.
nлин=2 8 – 8 – 6 =2.
ОС
ЗС
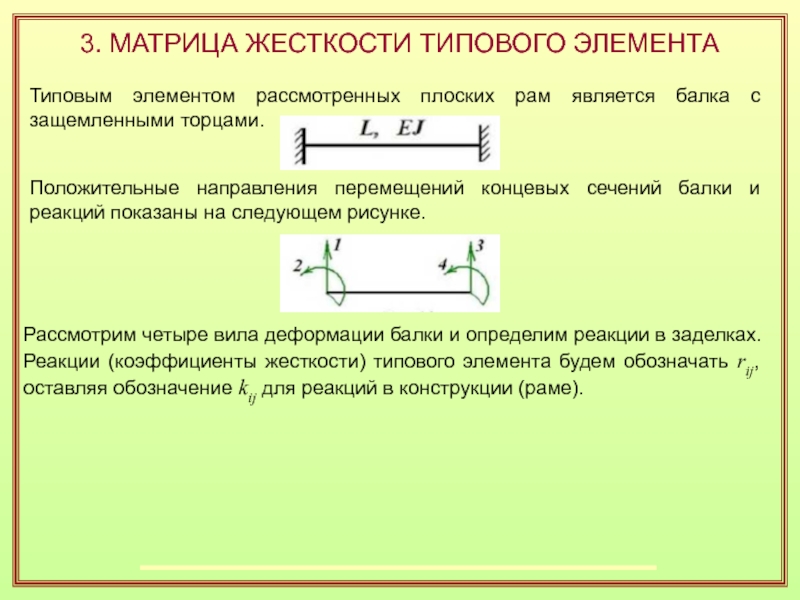
Слайд 243. МАТРИЦА ЖЕСТКОСТИ ТИПОВОГО ЭЛЕМЕНТА
Типовым элементом рассмотренных плоских рам является
балка с защемленными торцами.
Положительные направления перемещений концевых сечений балки
и реакций показаны на следующем рисунке.Рассмотрим четыре вила деформации балки и определим реакции в заделках. Реакции (коэффициенты жесткости) типового элемента будем обозначать rij, оставляя обозначение kij для реакций в конcтрукции (раме).
Слайд 25Используя дифференциальные соотношения для упругой линии балки:
-кривизна изогнутой оси:
-угол поворота
поперечного сечения:
-прогиб:
Первый вид деформации балки.
Левому торцу балки сообщается единичное
линейное перемещение. Искомые реакции показаны на рисунке. Поскольку реакции обусловлены смещением по направлению 1, то в обозначениях реакций второй индекс – 1.Составим уравнение изогнутой оси балки.
Изгибающий момент в сечении с координатой z
(по методу сечений):
Заметим, что при интегрировании были выполнены граничные условия на левом торце балки.
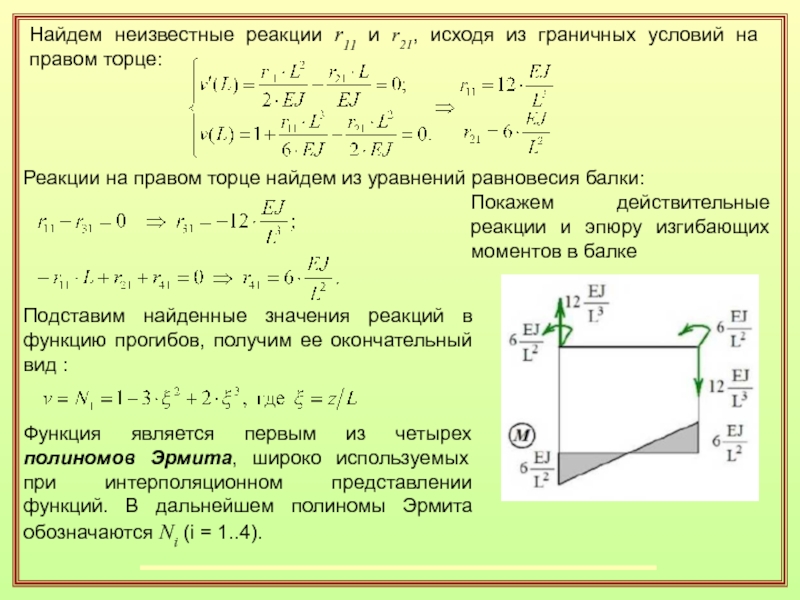
Слайд 26Найдем неизвестные реакции r11 и r21, исходя из граничных условий
на правом торце:
Реакции на правом торце найдем из уравнений
равновесия балки:Покажем действительные реакции и эпюру изгибающих моментов в балке
Подставим найденные значения реакций в функцию прогибов, получим ее окончательный вид :
Функция является первым из четырех полиномов Эрмита, широко используемых при интерполяционном представлении функций. В дальнейшем полиномы Эрмита обозначаются Ni (i = 1..4).
Слайд 27Второй вид деформации балки.
Левому торцу балки сообщается единичное угловое
перемещение. Искомые реакции показаны на рисунке.
Выполняя те же действия, что
в первом случае, находим:изгибающие моменты:
-кривизну изогнутой оси
-углы поворота поперечных сечений
-прогибы
Слайд 28Удовлетворяя граничные условия на правом торце, получаем значения реакций
Из
уравнений равновесия балки имеем:
Прогибы балки описываются вторым полиномом Эрмита:
Действительные
реакции и эпюра изгибающих моментов в балке показаны на рисунке.Слайд 29Третий вид деформации балки.
Правому торцу балки сообщается единичное линейное
перемещение. Искомые реакции показаны на рисунке.
Выполняя те же действия, что
в первом случае, находим реакции:Действительные реакции показаны на рисунке.
Прогибы балки при третьем виде деформации (третий полином Эрмита)
Слайд 30Четвертый вид деформации балки.
Правому торцу балки сообщается единичное угловое
перемещение. Искомые реакции показаны на рисунке.
По аналогии:
Действительные реакции показаны на
рисунке.Прогибы балки при четвертом виде деформации (четвертый полином Эрмита)
Слайд 31Реакции, найденные для всех четырех видов деформации балки, сведем в
матрицу жесткости элемента:
Составленная матрица жесткости элемента связывает вектор линейных и
угловых перемещений {Z} концевых сечений балки с вектором {r} поперечных сил и изгибающих моментов, действующих в тех же сечениях; т.е.Заметим, что матрица жесткости элемента является симметричной по факту построения. Основываясь на принципе взаимности работ, можно доказать свойство симметрии матрицы жесткости любой линейно упругой системы.
Слайд 324. РЕАКЦИИ СВЯЗЕЙ ОТ ЗАДАННЫХ ВНЕШНИХ СИЛ
Определим реакции в заделках
для балки, нагруженной в произвольном сечении сосредоточенной силой. Эта задача
является весьма важной, так как зная ее решение и используя принцип суперпозиции, можно получить результат для произвольной нагрузки.Поставленную задачу можно решить традиционными методами, например, методом сил или с помощью интегрирования дифференциального уравнения изогнутой оси балки. Мы воспользуемся методом, основанным на принципе взаимности работ.
В качестве внешних нагрузок, действующих на балку могут выступать сосредоточенные и распределенные силы и сосредоточенные изгибающие моменты.
Слайд 33Состояние балки при действии внешней силы будем называть первым.
Реакции определяются
поочередно. Для определения реакции r1F выберем в качестве второю состояния
форму деформации балки при единичном перемещении по направлению искомой реакции, т.е. по направлению 1 (см рисунок).Согласно принципу взаимности работ работа W12 сил первого состояния на соответствующих им перемещениях второго состояния равна работе W21 сил второго состояния на соответствующих им перемещениях первого состояния. Итак, W12 = W21.
Из пяти сил, действующих в первом состоянии на перемещениях во втором состоянии, совершают работу лишь две силы - искомая r1F и заданная F.
Имеем
где vF - перемещение в точке приложения силы F во втором состоянии.
Силы второго состояния не совершают работу на перемещениях первого состояния, поэтому W2 = 0.
Слайд 34Полученный результат позволяет сформулировать общее правило определения реакций:
Для определения
реакции связи необходимо вычислить работу заданной внешней нагрузки па перемещениях,
связанных с единичным смещением в направлении искомой реакции, и взять работу со знаком минус.Прогибы балки во втором состоянии были рассмотрены предыдущем вопросе.
Таким образом, прогиб во втором состоянии в точке приложения силы
а искомая реакция равна
Аналогично можно выразить остальные реакции, причем в качестве прогибов второго состояния последовательно рассматривают полиномы Эрмита. В результате имеем:
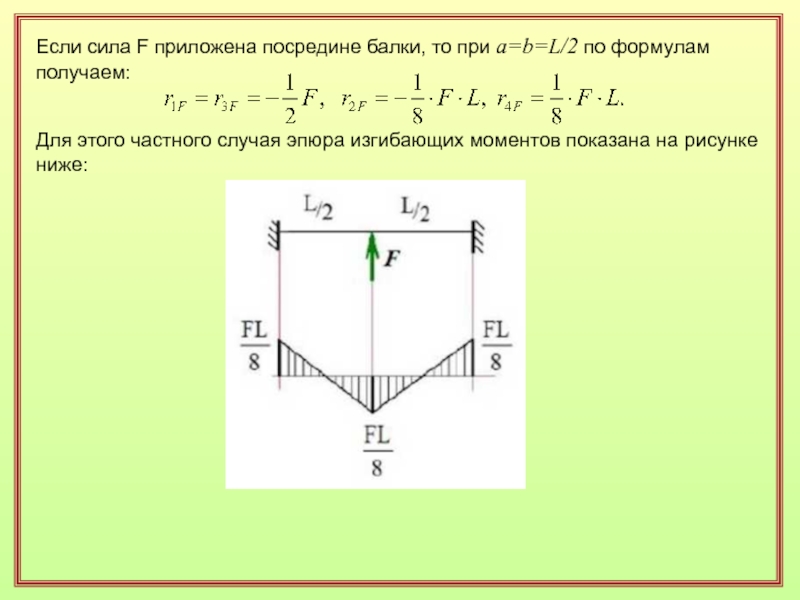
Слайд 36Если сила F приложена посредине балки, то при a=b=L/2 по
формулам получаем:
Для этого частного случая эпюра изгибающих моментов показана на
рисунке ниже:
Слайд 37Рассмотрим определение реакций в заделках при произвольной распределенной нагрузке q(z).
Применяя
изложенную процедуру принципа взаимности работ, вычисляем работу распределенной нагрузки на
прогибах балки при втором (виртуальном) состоянии, в качестве которого последовательно выбирается один из четырех изученных видов деформации балки:где Ni(z) - полиномы Эрмита; согласно сформулированному ранее
правилу определения реакций работа берется со знаком минус.
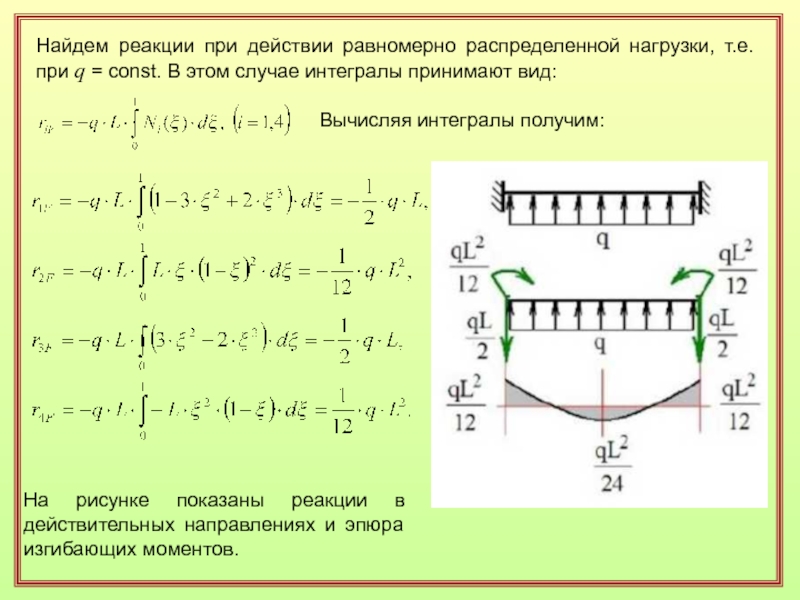
Слайд 38Найдем реакции при действии равномерно распределенной нагрузки, т.е. при q
= const. В этом случае интегралы принимают вид:
Вычисляя интегралы получим:
На
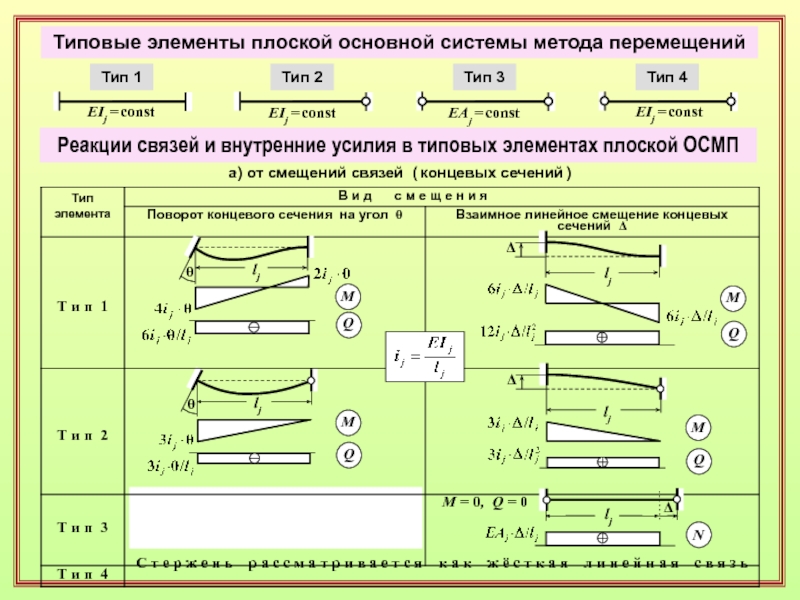
рисунке показаны реакции в действительных направлениях и эпюра изгибающих моментов.Слайд 39Типовые элементы плоской основной системы метода перемещений
EIj = const
Тип 1
EIj
= const
Тип 2
EАj = const
Тип 3
EIj = const
Тип 4
Реакции связей
и внутренние усилия в типовых элементах плоской ОСМПа) от смещений связей ( концевых сечений )
Q
lj
D
lj
q
lj
q
M
Q
M
lj
Q
M
D
Q
M
lj
D
N
С т е р ж е н ь р а с с м а т р и в а е т с я к а к ж ё с т к а я л и н е й н а я с в я з ь
M = 0, Q = 0
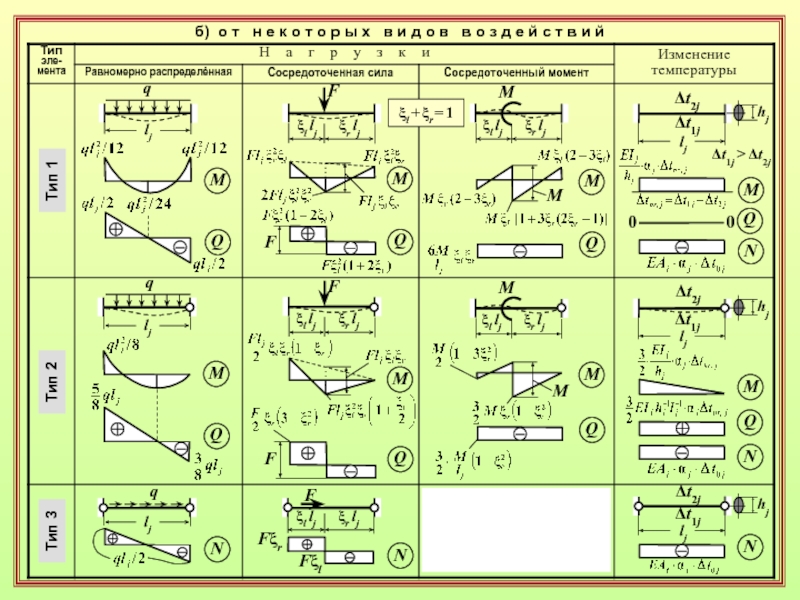
Слайд 40Тип 1
q
lj
Тип 2
б) о т н е к о
т о р ы х в и д о
в в о з д е й с т в и йxl lj
xr lj
F
M
M
Q
F
M
Q
M
Q
M
q
lj
M
Q
F
F
M
Q
M
M
Q
M
lj
q
F
N
N
Fxr
Тип 3
lj
hj
Dt2j
Dt1j
M
N
Q
0
0
lj
hj
Dt1j
M
N
Q
Dt2j
lj
hj
Dt1j
Dt2j
N
Dt1j > Dt2j
xl lj
xr lj
xl lj
xr lj
xl lj
xr lj
xl + xr = 1
xl lj
xr lj
Fxl
Слайд 41 Таким образом
Получены жесткости типового элемента плоских рам и
реакции в заделках элемента при действии внешних сил. Эти результаты
позволяют составлять уравнения метода перемещений для расчета рам. Решая эти уравнения находят найти перемещения узловПосле определения узловых перемещений, как правило, требуется построить эпюры изгибающих моментов в раме.
Решая вспомогательные задачи, мы установили распределение изгибающих моментов в типовом элементе при различных видах его деформации и нагружения.
Вспомним, что для формирования уравнений метода перемещений мы рассматривали состояния основной системы при действии внешних сил и при единичных перемещениях узлов. Эпюры моментов для каждого из этих состояний могут быть построены с привлечением найденных решений вспомогательных задач.
Обозначим функцию моментов в основной системе от заданных внешних сил через МF, функции моментов в основной системе при единичных перемещениях узлов через Mj, где индекс j указывает номер (направление)
узлового перемещения.
Моменты в рассчитываемой раме определяются путем суперпозиции:
где Zj - вычисленные узловые перемещения, n - общее число введенных узловых перемещений (степень кинематической неопределимости конструкции).
Слайд 42Сравним метод сил (МС) и метод перемещений (МП):
1) Оба
используются для расчета статически неопределимых систем. При принятии одинаковых допущений,
оба приводят к единому результату. При использовании в разных областях дополняют друг-друга.2) В МС неизвестными являются силы, а в МП – перемещения. При расчете одной и той же системы число их неизвестных часто бывает разным. Значит, одни системы выгоднее рассчитывать МС, другие МП.
3) В МС ОС получается удалением связей, а в МП – введением связей. В МС вариантов ОС много, а в МП она единственна.
4) Единичные состояния (ЕС) в МС определяются воздействием единичных сил, в МП – единичных перемещений.
5) В МС необходимые эпюры в ОС строятся обычным способом, а в МП – по готовой таблице.
6) Коэффициенты канонических уравнений в МП определяются проще (из уравнений статики).
7) Многие боковые коэффициенты системы канонических уравнений МП равняются нулю, что упрощает ее решение и т.д.
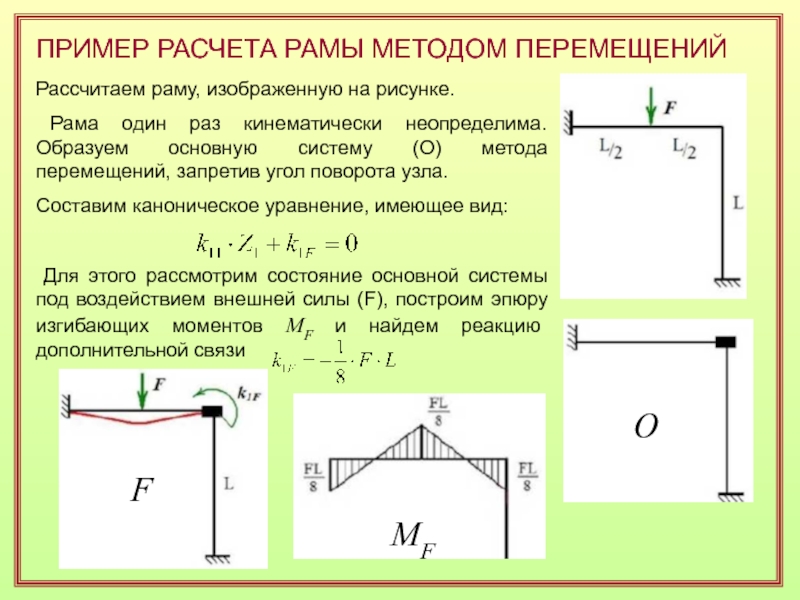
Слайд 43ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Рассчитаем раму, изображенную на рисунке.
Рама
один раз кинематически неопределима. Образуем основную систему (O) метода перемещений,
запретив угол поворота узла.Составим каноническое уравнение, имеющее вид:
Для этого рассмотрим состояние основной системы под воздействием внешней силы (F), построим эпюру изгибающих моментов МF и найдем реакцию дополнительной связи
O
F
MF
Слайд 44Далее рассмотрим состояние основной системы при единичном угле поворота узла
(1), построим соответствующую эпюру моментов М1 и найдем момент в
дополнительной заделке:1
M1
Полный реактивный момент в заделке равен нулю, поэтому:
Найдем угол поворота узла рамы:
Вычислим изгибающие моменты в заданной раме по правилу суперпозиции:
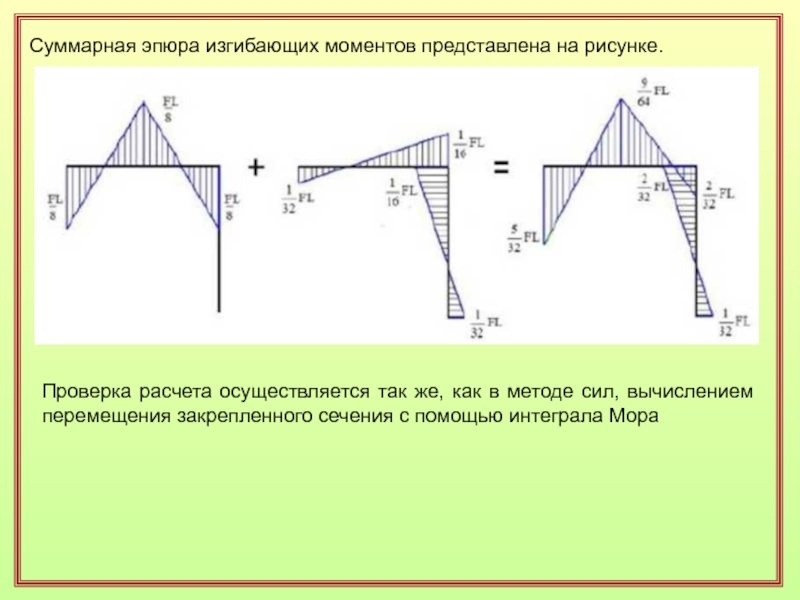
Слайд 45Суммарная эпюра изгибающих моментов представлена на рисунке.
Проверка расчета осуществляется
так же, как в методе сил, вычислением перемещения закрепленного сечения
с помощью интеграла МораСлайд 46ЗАКЛЮЧИТЕЛЬНОЕ ЗАМЕЧАНИЕ
Идея расчета конструкций с использованием перемещений узлов в качестве
основных искомых величин получила развитие в наиболее мощном современном методе
анализа напряженного состояния конструкций - методе конечных элементов (МКЭ). При расчете с помощью МКЭ конструкцию представляют как совокупность конечных (типовых) элементов, связанных между собой в узлах. Специалистами разработаны многочисленные типы конечных элементов, предназначенных для расчета конструкций по стержневым, оболочечным, трехмерным и комбинированным моделям. Важно, что для любого конечного элемента методами теории упругости устанавливается связь между перемещениями узлов {Z}(e) и действующими в узлах силами {F}(e):Здесь [k](e) - матрица жесткости конечного элемента, верхний индекс указывает на отношение величины к отдельному конечному элементу.
Данное соотношение аналогично по смыслу соотношению для типового элемента рамы.
К сожалению, решить матричные уравнения МКЭ относительно перемещений {Z}(e) невозможно, т.к. в вектор {F}(e) помимо известных внешних сил входят неизвестные силы взаимодействия рассматриваемого элемента с соседними конечными элементами. Поэтому необходима так называемая процедура сборки конечных элементов.
Слайд 47Из множества конечных элементов собирается расчетная модель конструкции, для которой
уравнения МКЭ имеют вид, схожий с уравнениями метода перемещений:
здесь {Z}
- вектор перемещений всех узлов конструкции, т.е. ансамбля конечных элементов; {F} - вектор внешних нагрузок, приведенных к узлам конструкции; [К] - матрица жесткости конструкции.При сборке конечных элементов неизвестные внутренние силы взаимодействия между элементами взаимно уничтожаются, т.е. исчезают из уравнений. Система уравнений становится замкнутой.
Заметим, что канонические уравнения метода перемещений приобретают вид, характерный для МКЭ, если вместо вектора реакции {КF} ввести противоположный вектор {F}=-{KF}, компоненты которого следует трактовать как внешние узловые силы, т.е. силы, приведенные к узлам рамы
Слайд 48К о н т р о л ь н ы
е в о п р о с ы
1. В чем сущность метода перемещений ? 2. Что принимается за основные неизвестные в методе перемещений?
3. Признаки расчетных узлов системы.
4. Что такое кинематически неопределимая система (КНС)?
5. Какая система называется кинематически определимой?
6. Что такое степень кинематической неопределимости?
7. Что такое шарнирная система, как она получается и для чего используется?
8. Как при формировании шарнирной системы учитываются элементы, удлинениями которых при растяжении (сжатии) нельзя пренебрегать?
9. Какую рабочую гипотезу вводят в МП для стержней, работающих преимущественно на изгиб, и каково следствие применения этой гипотезы (влияние на количество основных неизвестных)?
10. Что такое основная система метода перемещений (ОСМП)?
Сколько основных систем можно составить для заданной системы?
11. Что такое матрица жёсткости стержня?
12. Типы элементов ОСМП, табличные эпюры и способы их получения
13. Определение основных неизвестных МП и искомых усилий