Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СТРУКТУРЫ ДАННЫХ Лектор Спиричева Наталия Рахматулловна Ст. преподаватель каф
Содержание
- 1. СТРУКТУРЫ ДАННЫХ Лектор Спиричева Наталия Рахматулловна Ст. преподаватель каф
- 2. Структуры данных Структуры данныхСоставитель курса лекций:Спиричева Наталия Рахматулловна, ст. преподаватель каф. Информационных технологий
- 3. Структуры данных Структуры данныхДревовидные структуры данных
- 4. Структуры данных Структуры данных и алгоритмы Целью лекции является
- 5. Структуры данных Структуры данных и алгоритмыОсновные темы лекции:Понятие древовидных структурДеревьяГрафыАлгоритмы поиска путей в графах
- 6. Структуры данных ВведениеДерево - конечное множество, состоящее из
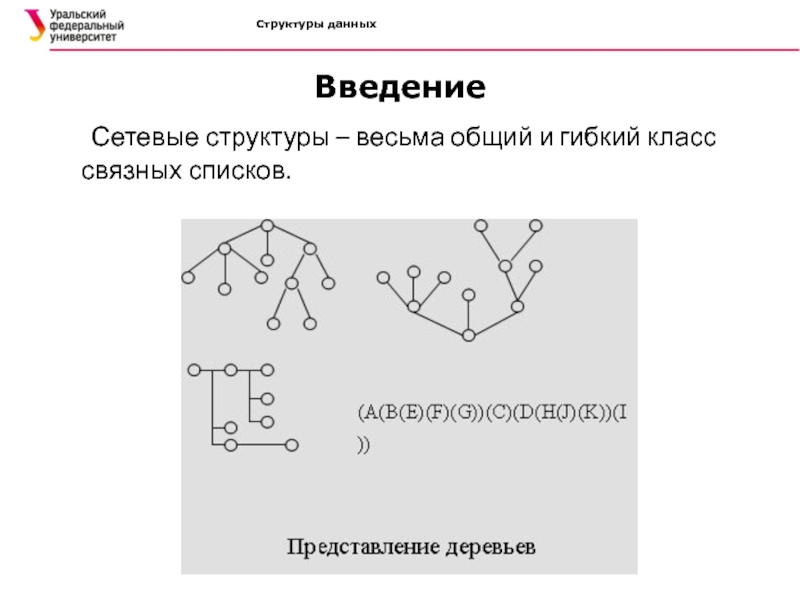
- 7. Структуры данных Введение Сетевые структуры – весьма общий и гибкий класс связных списков.
- 8. Структуры данных Введение Определим дерево как конечное множество Т,
- 9. Структуры данных Из определения следует:Каждый узел дерева является
- 10. Структуры данных Введение Обычно дерево представляется в машинной памяти
- 11. Структуры данных Введение Сетевые структуры – весьма общий и гибкий класс связных списков.
- 12. Структуры данных Введение Лес – это
- 13. Структуры данных Бинарное дерево Бинарное дерево - конечное множество
- 14. Структуры данных Бинарное дерево В алгоритмах работы с древовидными
- 15. Структуры данных Бинарное деревоПрямой порядок обхода:Попасть в кореньПройти
- 16. Структуры данных Бинарное дерево“Прошитые” деревья В “прошитых” деревьях концевые
- 17. Структуры данных ДеревьяГрафы
- 18. Структуры данных ГрафыГраф - некоторое множество точек (называемых
- 19. Структуры данных Графы Каждая пара вершин
- 20. Структуры данных Графы Пусть V и
- 21. Структуры данных ГрафыГраф называется связным, если имеется путь
- 22. Структуры данных Графы
- 23. Структуры данных ГрафыЗадание графа: Класс матриц инциденции. Если граф
- 24. Структуры данных Графы
- 25. Структуры данных Графы Класс матриц смежности. Матрица смежности S=[sij]nxm
- 26. Структуры данных Графы
- 27. Структуры данных ДеревьяАлгоритмы поиска путей в графе
- 28. Структуры данных Алгоритмы поиска путей в графе Путь
- 29. Структуры данных Волновой алгоритмКаждой вершине i приписывается два
- 30. Структуры данных Под корректностью алгоритма здесь понимается, что:
- 31. Структуры данных Алгоритмы поиска путей в графе Путь
- 32. Структуры данных Алгоритмы поиска путей в графе Алгоритм,
- 33. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 34. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 35. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 36. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 37. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 38. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 39. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 40. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 41. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 42. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 43. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 44. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 45. Структуры данных Алгоритмы поиска путей в графе Путь
- 46. Структуры данных Алгоритмы поиска путей в графе Нахождение
- 47. Структуры данных Алгоритмы поиска путей в графе Алгоритм:1.
- 48. Структуры данных 1.Какими структурами данных можно представить в
- 49. Спасибо за внимание!Структуры данных
- 50. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Структуры данных
Структуры данных
Составитель курса лекций:
Спиричева Наталия Рахматулловна,
ст. преподаватель каф.
Информационных технологий
Слайд 4Структуры данных
Структуры данных и алгоритмы
Целью лекции является приобретение студентами следующих
компетенций:
знать методы представления древовидных структур в памяти ЭВМ
знать и уметь
применять алгоритмы поиска путей в графахСлайд 5Структуры данных
Структуры данных и алгоритмы
Основные темы лекции:
Понятие древовидных структур
Деревья
Графы
Алгоритмы поиска
путей в графах
Слайд 6Структуры данных
Введение
Дерево - конечное множество, состоящее из одного или более
элементов, называемых узлами.
Корень - узел, не имеющий исходного. Все узлы,
кроме корня, имеют только один исходный. Есть деревья, состоящие из одного корня. Каждый узел может иметь несколько порождённых. Слайд 8Структуры данных
Введение
Определим дерево как конечное множество Т, состоящее из одного
или более узлов, таких, что
а) имеется один специально обозначенный
узел, называемый корнем данного дерева,б) остальные узлы (исключая корень) содержатся в m0 попарно непересекающихся множествах Т1, …, Тm, каждое из которых в свою очередь является деревом. Деревья Т1, …, Тm называются поддеревьями данного корня.
Слайд 9Структуры данных
Из определения следует:
Каждый узел дерева является корнем некоторого поддерева,
которое содержится в этом дереве.
Число поддеревьев данного узла называется
степенью этого узла. Узел с нулевой степенью называется концевым узлом;
Неконцевые узлы часто называют узлами разветвления.
Уровень узла по отношению к дереву Т определяется следующим образом: говорят, что корень имеет уровень 1, а другие узлы имеют уровень на 1 выше их уровня относительно содержащего их поддерева Тj этого корня.
Слайд 10Структуры данных
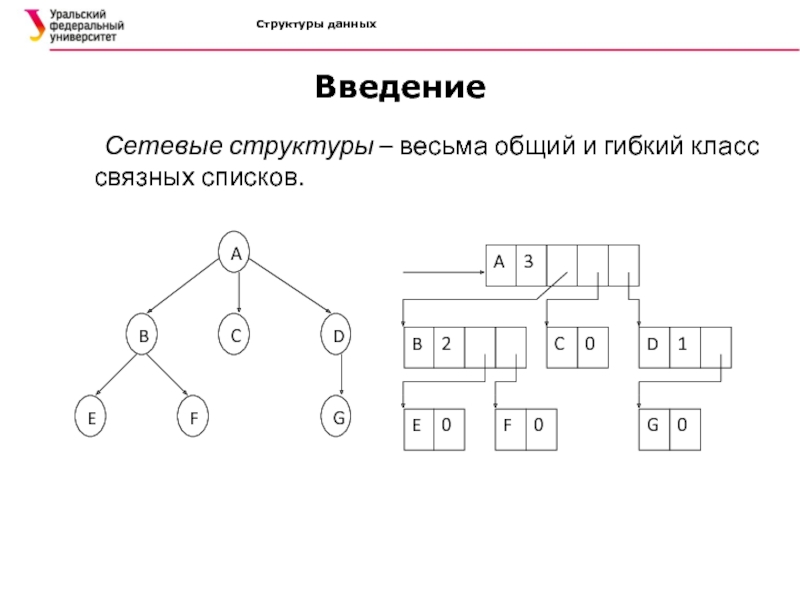
Введение
Обычно дерево представляется в машинной памяти в форме многосвязного
списка, в котором каждый указатель соответствует дуге. Это представление называется
естественным представлением дерева. Существуют несколько разновидностей такого представления. В одной из наиболее общих разновидностей каждому узлу дерева ставится в соответствие элемент многосвязного списка, причем в каждом элементе отводятся следующие поля: поле данных, поле степени исхода (т.е. числа сыновей) и поля указателей, число которых равно степени исхода.Слайд 12Структуры данных
Введение
Лес – это множество (обычно упорядоченное),
состоящее из некоторого (быть может равного нулю) числа непересекающихся деревьев.
Слайд 13Структуры данных
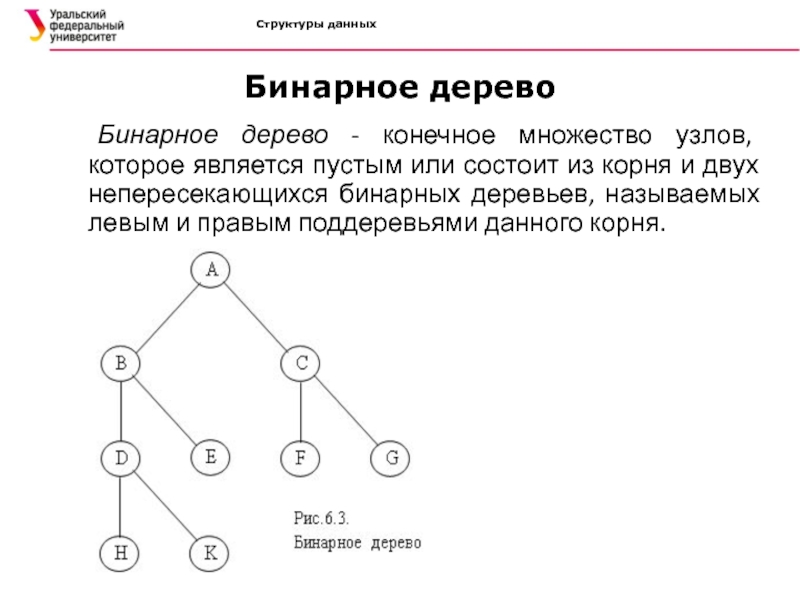
Бинарное дерево
Бинарное дерево - конечное множество узлов, которое является
пустым или состоит из корня и двух непересекающихся бинарных деревьев,
называемых левым и правым поддеревьями данного корня.Слайд 14Структуры данных
Бинарное дерево
В алгоритмах работы с древовидными структурами наиболее часто
встречается понятие обход дерева.
Для обхода бинарных деревьев можно применить
один из
трех принципиально разных способов:в прямом порядке
в центрированном порядке
в обратном порядке
Слайд 15Структуры данных
Бинарное дерево
Прямой порядок обхода:
Попасть в корень
Пройти левое поддерево
Пройти правое
поддерево
Центрированный порядок обхода:
Пройти левое поддерево
Попасть в корень
Пройти правое поддерево
Обратный порядок
обхода:Пройти левое поддерево
Пройти правое поддерево
Попасть в корень
Слайд 16Структуры данных
Бинарное дерево
“Прошитые” деревья
В “прошитых” деревьях концевые связи-указатели используются для
связи с родителями, такие связи назвали нитями.
Отличие нормальных связей
от нитей: в каждом узле хранят две однобитовые переменные LTag и RTag. Эти переменные равны нулю, если соответствующие связи указывают на поддеревья, и единице, если связи являются нитями. Левая нить каждого узла указывает на узел, являющийся предшественником данного при центрированном обходе, правая - на узел, являющийся последователем данного узла.
Слайд 18Структуры данных
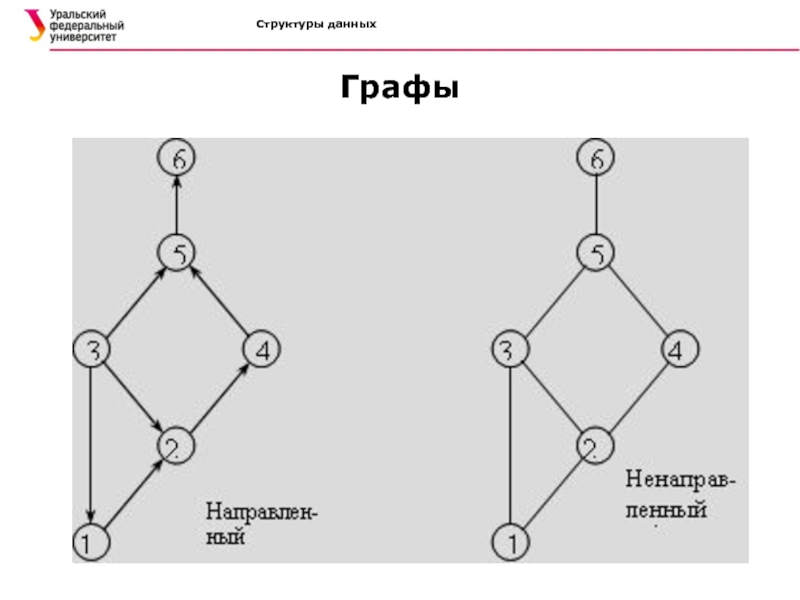
Графы
Граф - некоторое множество точек (называемых вершинами) и некоторое
множество линий (называемых ребрами), соединяющих определенные пары вершин. Каждая пара
вершин соединяется не больше чем одним ребром.Графы:
взвешенные и невзвешенные
ориентированные и неориентированные
Слайд 19Структуры данных
Графы
Каждая пара вершин в графе соединяется
не больше чем одним ребром. Дуга, соединенная с вершиной, называется
инцидентной этой вершине. Две вершины называются смежными, если существует ребро, соединяющее их. Две дуги называются смежными, если они инцидентны одной и той же вершине.Слайд 20Структуры данных
Графы
Пусть V и V` - вершины
и пусть n0; говорят, что «V0, V1, …, Vn» -
путь длины n от V до V`, если V=V0, вершина Vk смежна с Vk+1 при 0kn, а Vn=V`. Путь прост, если вершины V0, V1, …, Vn-1 все различны между собой, а также различны все вершины V1, V2, …, Vn. Граф называется связным, если имеется путь между каждыми двумя вершинами этого графа. Циклом называется простой путь длины не менее 3 от какой-либо вершины до нее самой. Свободное дерево – это связный граф, не имеющий циклов.Слайд 21Структуры данных
Графы
Граф называется связным, если имеется путь между каждыми двумя
вершинами этого графа.
Циклом называется простой путь длины не менее
3 от какой-либо вершины до нее самой. Свободное дерево – это связный граф, не имеющий циклов.Формально направленный граф определяется как некое множество вершин и множество дуг, причем каждая дуга ведет от некоторой вершины V к некоторой вершине V`. Если e – дуга, идущая от V к V`, то говорят, что V – начальная вершина дуги e, а V` - конечная вершина.
Слайд 23Структуры данных
Графы
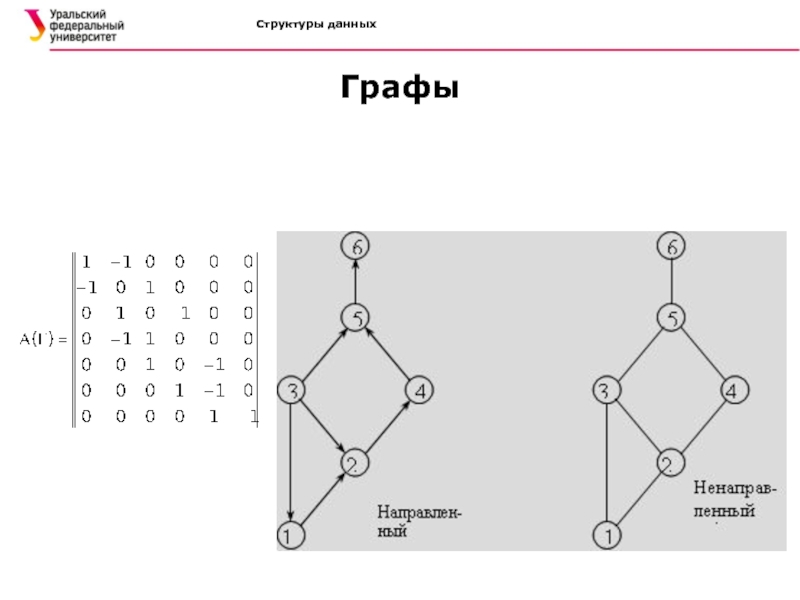
Задание графа:
Класс матриц инциденции. Если граф Г содержит n
вершин и m дуг, то матрица инциденции А(Г)=[aij]mxn определяется так:
Слайд 25Структуры данных
Графы
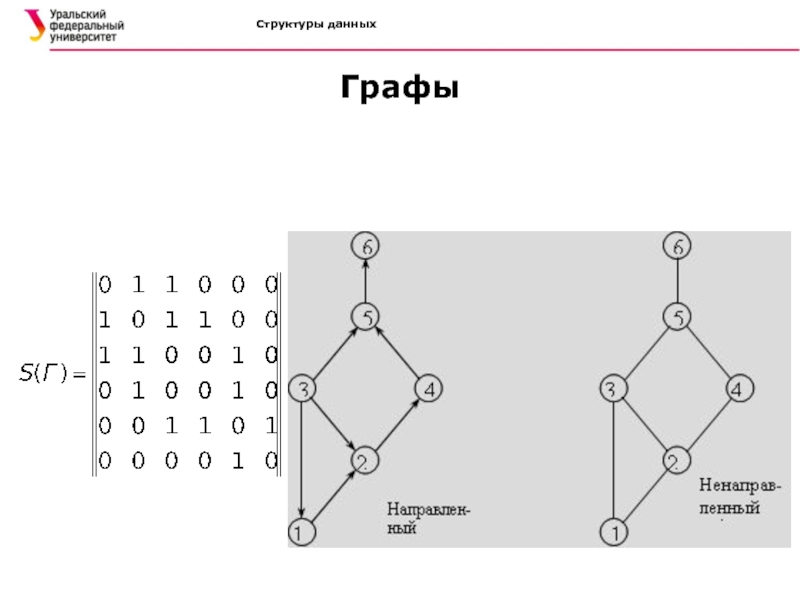
Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется
следующим образом:
Во взвешенном графе каждая единица заменяется на вес соответствующего
ребра Слайд 28Структуры данных
Алгоритмы поиска путей в графе
Путь с минимальным количеством
промежуточных вершин
Алгоритм просматривает вершины графа в таком порядке:
соединённые
с исходной вершинойсоединённые с уже просмотренными, но ещё не просмотренные.
Слайд 29Структуры данных
Волновой алгоритм
Каждой вершине i приписывается два целых числа Times[i]
- временная метка и Previous [i] - метка предыдущей вершины
пути (начальное значение Times[i]=0, Previous [i]=0 для всех i).Заводятся два списка "фронта волны" NewFront и OldFront, а также переменная Time (текущее время).
OldFront:={ver1}; NewFront:={}; Time:=1.
Для каждой из вершин i, входящих в OldFront, просматриваются соседние вершины j, и если Times [j] = 0, то Times [j]=Time, NewFront := NewFront + {j}; в переменную Previous [j] заносится номер i.
Если NewFront = {}, то путь не существует, переход к шагу 8.
Если одна из веpшин совпадает с ver2, то найден кратчайший путь длины Time, переход к шагу 8.
OldFront:= NewFront; NewFront:={}; Time:=Time+1; возврат к шагу 4.
Восстанавливаем путь, проходя массив P.
Слайд 30Структуры данных
Под корректностью алгоритма здесь понимается, что:
алгоритм завершает работу
за конечное время;
если решение существует, то алгоритм находит правильное решение.
Слайд 31Структуры данных
Алгоритмы поиска путей в графе
Путь минимальной суммарной длины
во взвешенном графе с неотрицательными весами (алгоритм Дейкстры)
Функция находит путь
минимального веса в графе G=(V,E), заданном весовой матрицей w, у которой элемент wi j равен весу ребра, соединяющего i-ю и j-ю вершины. При этом предполагается, что все элементы wi j неотрицательны. Путь ищется из вершины номер u1 к вершине номер u2. Функция использует алгоритм Дейкстры. Для бесконечности используется число GM, его можно задавать в зависимости от конкретной задачи.Слайд 32Структуры данных
Алгоритмы поиска путей в графе
Алгоритм, по которому происходит
поиск, заключается в следующем:
всем веpшинам пpиписывается вес - вещественное число,
d(i)=GM для всех вершин кроме вершины с номером u1, а d(u1)=0; всем веpшинам пpиписывается метка m(i)=0;
вершина u1 объявляется текущей - t=u1;
для всех вершин у которых m(i)=0, пересчитываем вес по формуле: d(i):=min{d(i), d(t)+W[t,i]};
среди вершин для которых выполнено m(i)=0, ищем ту, для которой d(i) минимальна, если минимум не найден, т.е. вес всех “непомеченных” вершин равен бесконечности (GM), то путь не существует; ВЫХОД;
иначе найденную вершину c минимальным весом полагаем текущей и помечаем (m(t)=1);
если t = u2, то найден путь веса d(t),ВЫХОД;
переходим на шаг 4.
Слайд 33Структуры данных
Алгоритмы поиска путей в графе
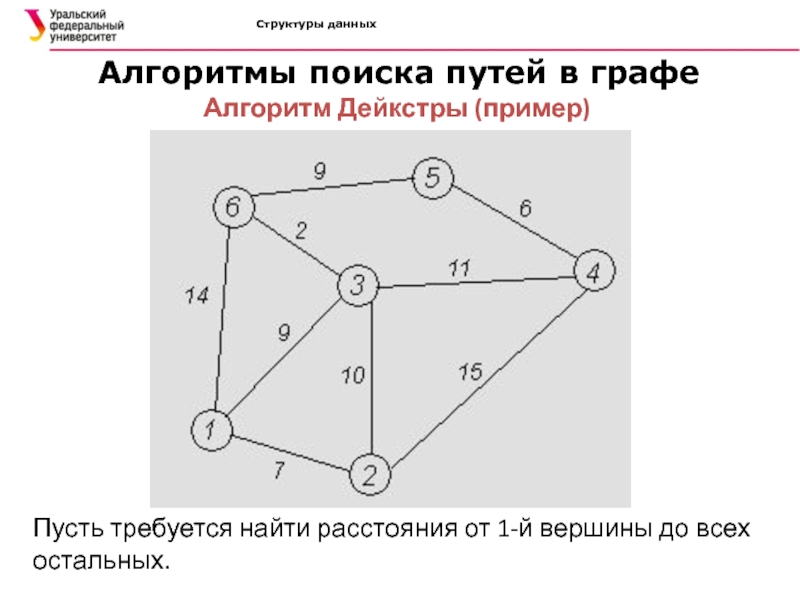
Алгоритм Дейкстры (пример)
Пусть требуется
найти расстояния от 1-й вершины до всех остальных.
Слайд 34Структуры данных
Алгоритмы поиска путей в графе
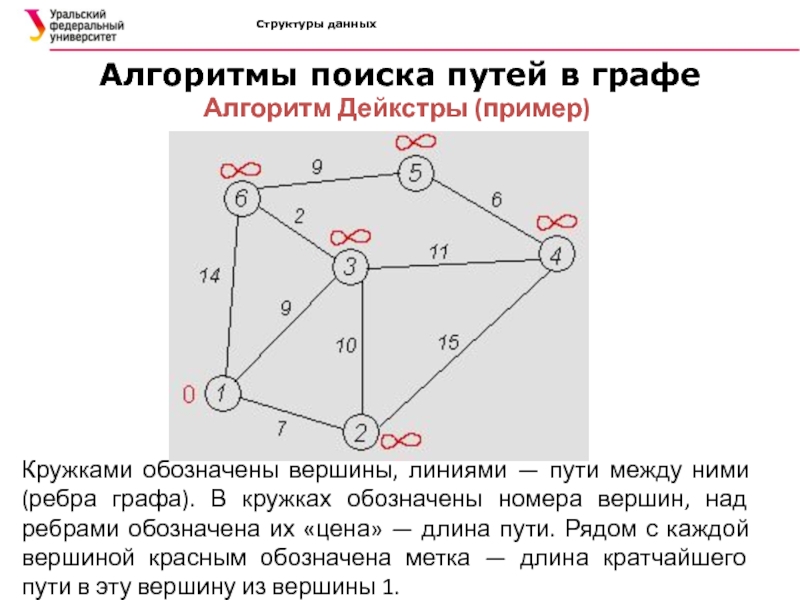
Алгоритм Дейкстры (пример)
Кружками обозначены
вершины, линиями — пути между ними (ребра графа). В кружках
обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.Слайд 35Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
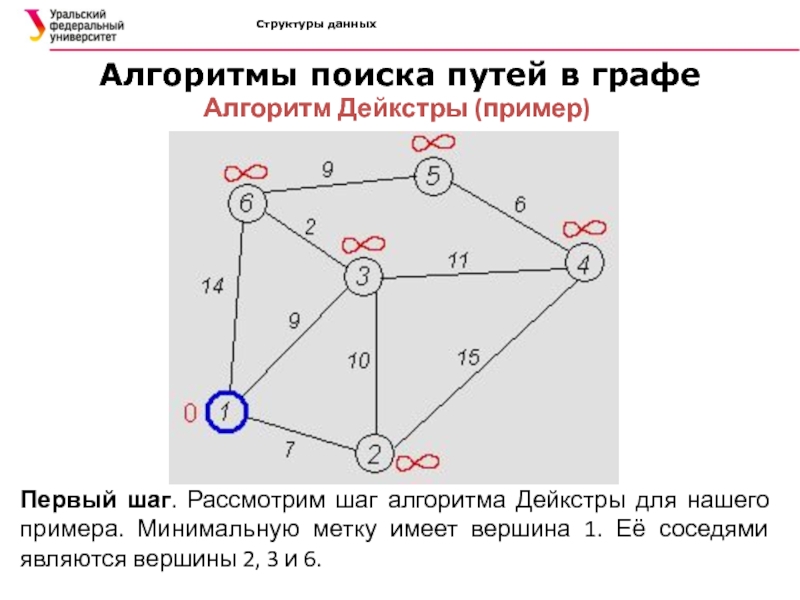
Первый шаг.
Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет
вершина 1. Её соседями являются вершины 2, 3 и 6.Слайд 36Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
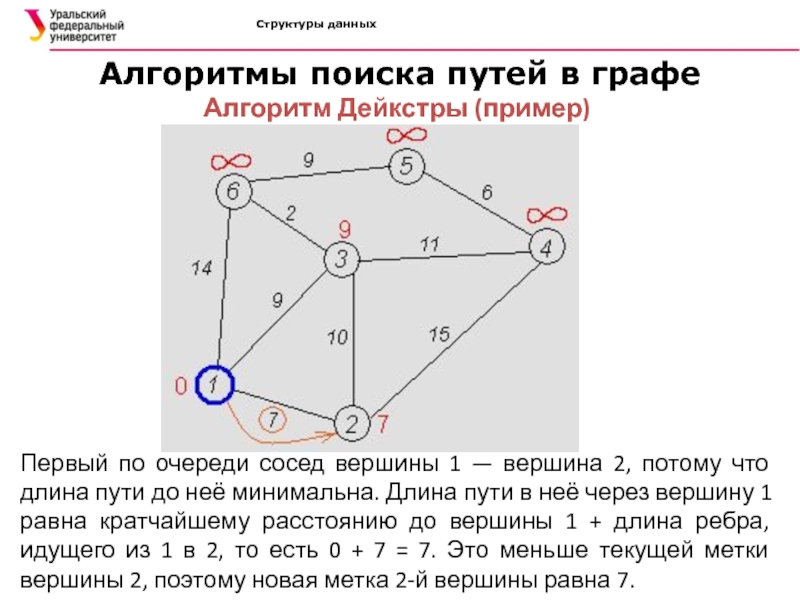
Первый по
очереди сосед вершины 1 — вершина 2, потому что длина
пути до неё минимальна. Длина пути в неё через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.Слайд 37Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
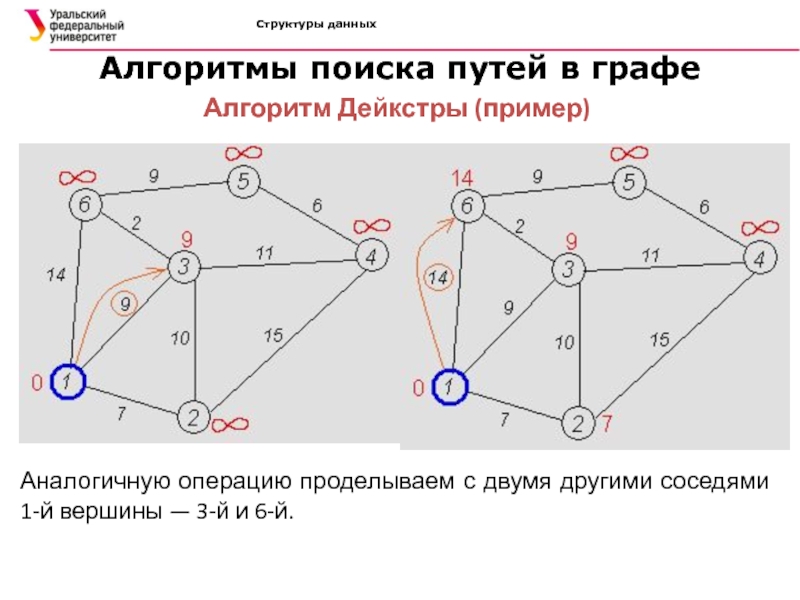
Аналогичную операцию
проделываем с двумя другими соседями 1-й вершины — 3-й и
6-й.Слайд 38Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
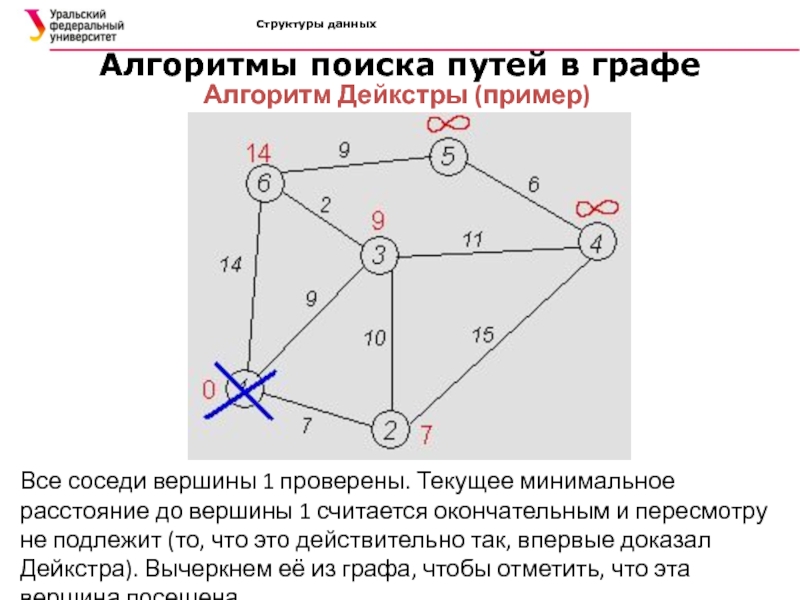
Все соседи
вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается
окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.Слайд 39Структуры данных
Алгоритмы поиска путей в графе
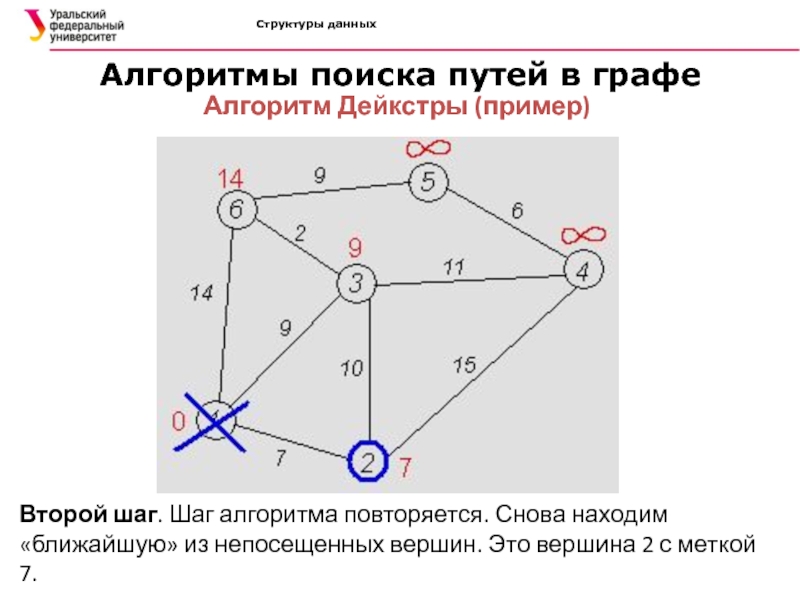
Алгоритм Дейкстры (пример)
Второй шаг.
Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это
вершина 2 с меткой 7.Слайд 40Структуры данных
Алгоритмы поиска путей в графе
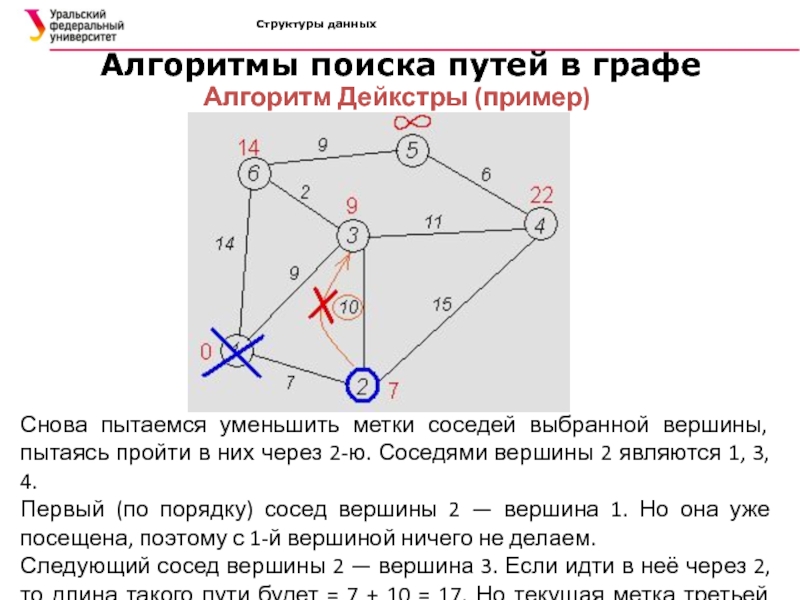
Алгоритм Дейкстры (пример)
Снова пытаемся
уменьшить метки соседей выбранной вершины, пытаясь пройти в них через
2-ю. Соседями вершины 2 являются 1, 3, 4.Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
Слайд 41Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
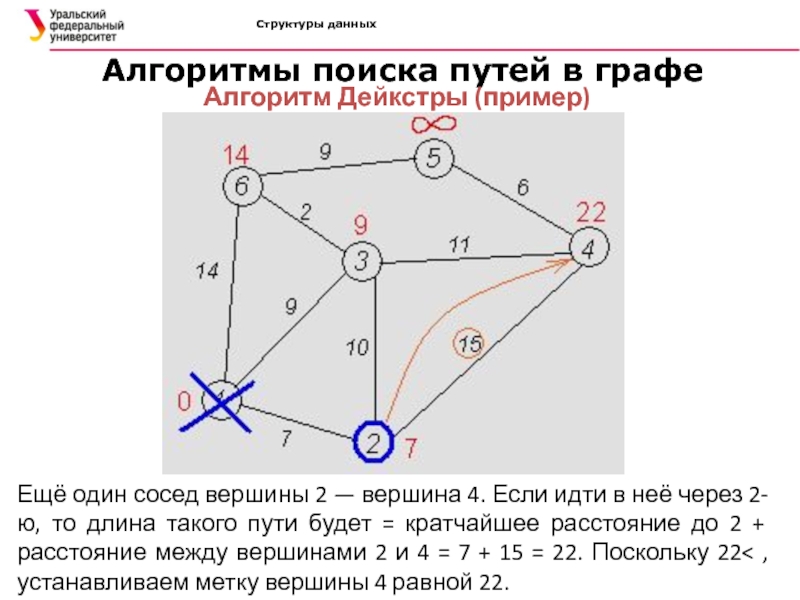
Ещё один
сосед вершины 2 — вершина 4. Если идти в неё
через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22< , устанавливаем метку вершины 4 равной 22.Слайд 42Структуры данных
Алгоритмы поиска путей в графе
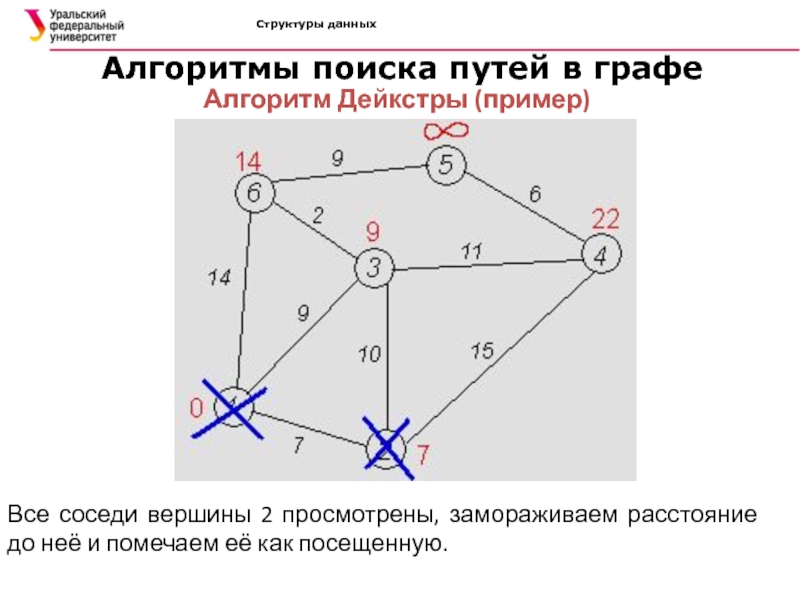
Алгоритм Дейкстры (пример)
Все соседи
вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её
как посещенную.Слайд 43Структуры данных
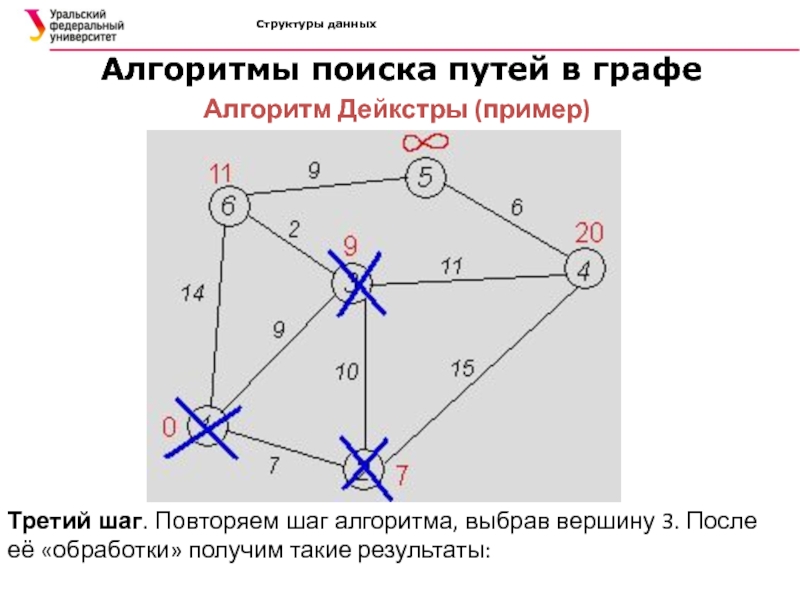
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
Третий шаг.
Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим
такие результаты:Слайд 44Структуры данных
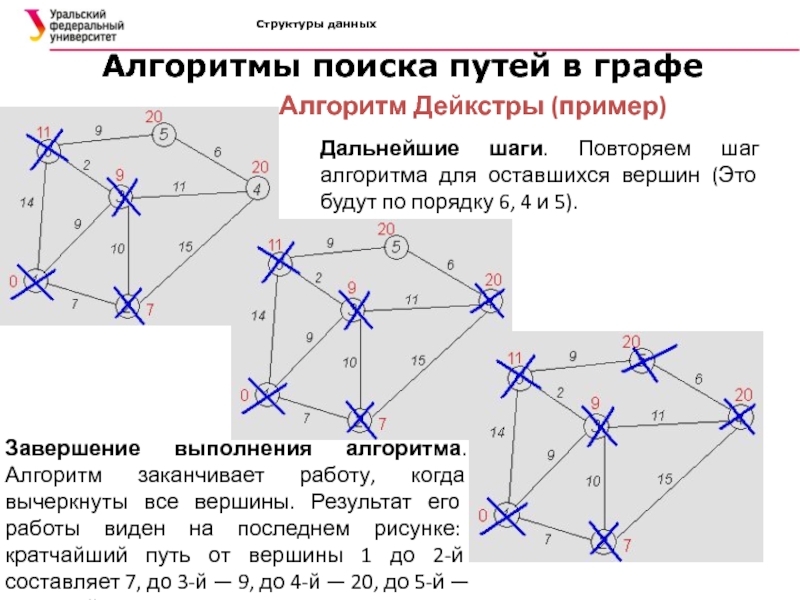
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
Дальнейшие шаги.
Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку
6, 4 и 5).Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Слайд 45Структуры данных
Алгоритмы поиска путей в графе
Путь минимальной суммарной длины
во взвешенном графе с произвольными весами для всех пар вершин
(алгоритм Флойда) Функция находит пути минимального веса в графе G=(V,E), заданном весовой матрицей w, у которой элемент wi j равен весу ребра, соединяющего i-ю и j-ю вершины. При этом полагаем, что W[i,i]=0 для всех i. Путь ищется для всех пар вершин графа. Для бесконечности используется число GM, его можно задавать в зависимости от конкретной задачи.Алгоритм Флойда предполагает последовательное преобразование матрицы весов W. В конечном итоге получаем матрицу, элементы d[i,j] которой представляют из себя вес минимального пути соединяющего i и j вершины.
Слайд 46Структуры данных
Алгоритмы поиска путей в графе
Нахождение K путей минимальной
суммарной длины во взвешенном графе с неотрицательными весами (алгоритм Йена)
Алгоритм предназначен для нахождения К путей минимальной длины во взвешенном графе между вершинами u1,u2. Ищутся пути, которые не содержат петель. Работа алгоритма начинается с нахождения кратчайшего пути, для этого будем использовать уже описанный алгоритм Дейкстры. Второй путь ищем, перебирая кратчайшие отклонения от первого, третий - кратчайшие отклонения от второго, и т.д.
Слайд 47Структуры данных
Алгоритмы поиска путей в графе
Алгоритм:
1. Найти минимальный путь
P1=(v11,...,v1L[1]). Положить k = 2. Включить P1 в результирующий список.
2.
Положить MinW равным бесконечности. Найти отклонение минимального веса от (k–1)-го кратчайшего пути Pk-1 для всех i=1,2,...,L[k-1], выполняя для каждого i шаги с 3-го по 6-й.3. Проверить, совпадает ли подпуть, образованный первыми i вершинами пути Pk-1, с подпутем, образованным первыми i вершинами любого из путей j=1,2,...,k–1). Если да, положить W[vk-1i,vji+1] равным бесконечности, в противном случае ничего не изменять (чтобы в дальнейшем исключить получение в результате одних и тех же путей).4. Используя алгоритм нахождения кратчайшего пути, найти пути от vk-1i к u2, исключая из рассмотрения корни (vk-11,...,vk-1i) (чтобы исключить петли), для этого достаточно положить равными бесконечности элементы столбцов и строк матрицы W, соответствующие вершинам, входящим в корень.
5. Построить путь, объединяя корень и найденное кратчайшее ответвление; если его вес меньше MinW, то запомнить его.
6. Восстановить исходную матрицу весов W и возвратиться к шагу 3.
7. Поместить путь минимального веса (MinW), найденный в результате выполнения шагов с 3 по 6, в результирующий список. Если k = K, то алгоритм заканчивает работу, иначе увеличить k на единицу и вернуться к шагу 2.
Слайд 48Структуры данных
1.Какими структурами данных можно представить в памяти древовидные структуры?
2.
Перечислите основные алгоритмы поиска путей в графах?
3. Какие основные классами
матриц предствляются графы в памяти компьютера?Контрольные вопросы



















![СТРУКТУРЫ ДАННЫХ
Лектор
Спиричева Наталия Рахматулловна
Ст. преподаватель каф Структуры данных Графы Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется следующим Структуры данных Графы Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется следующим образом: Во взвешенном графе каждая единица заменяется](/img/thumbs/238e4e0ceccbd23fae81c598070df84f-800x.jpg)


![СТРУКТУРЫ ДАННЫХ
Лектор
Спиричева Наталия Рахматулловна
Ст. преподаватель каф Структуры данных Волновой алгоритмКаждой вершине i приписывается два целых числа Times[i] - Структуры данных Волновой алгоритмКаждой вершине i приписывается два целых числа Times[i] - временная метка и Previous [i] -](/img/thumbs/243bd3ed729e01ea33661e4ffee578ae-800x.jpg)





![СТРУКТУРЫ ДАННЫХ
Лектор
Спиричева Наталия Рахматулловна
Ст. преподаватель каф Структуры данных Алгоритмы поиска путей в графе Алгоритм:1. Найти минимальный путь P1=(v11,...,v1L[1]). Структуры данных Алгоритмы поиска путей в графе Алгоритм:1. Найти минимальный путь P1=(v11,...,v1L[1]). Положить k = 2. Включить P1](/img/thumbs/febfb02f76833bd0b4d31e50f297db7c-800x.jpg)





















