Слайд 1
Ступені свободи руху абсолютно твердого тіла
Момент сили. Момент
інерції
Закон динаміки обертального руху
Умови рівноваги твердого тіла. Центр ваги. Види
рівноваги
Момент імпульсу. Закон збереження моменту імпульсу
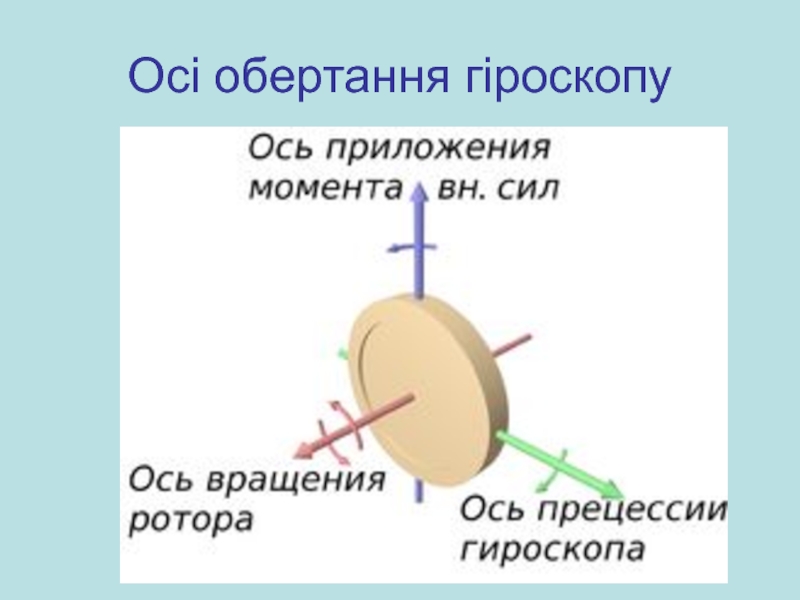
Уявлення про гіроскопи
Лекція № 6
Динаміка обертального руху
Слайд 21. Ступені свободи руху абсолютно твердого тіла.
Числом ступенів свободи
абсолютно твердого тіла називають найменше число координат, які необхідно задати
для того, щоб повністю визначити положення тіла у просторі, або кількість незалежних рухів, які може виконувати тіло.
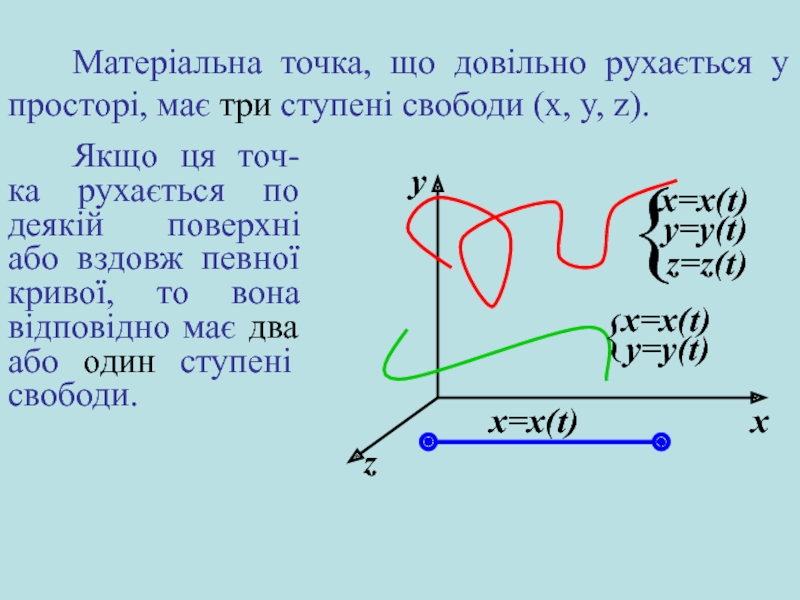
Слайд 3Матеріальна точка, що довільно рухається у просторі, має три ступені
свободи (x, y, z).
Якщо ця точ-ка рухається по деякій
поверхні або вздовж певної кривої, то вона відповідно має два або один ступені свободи.
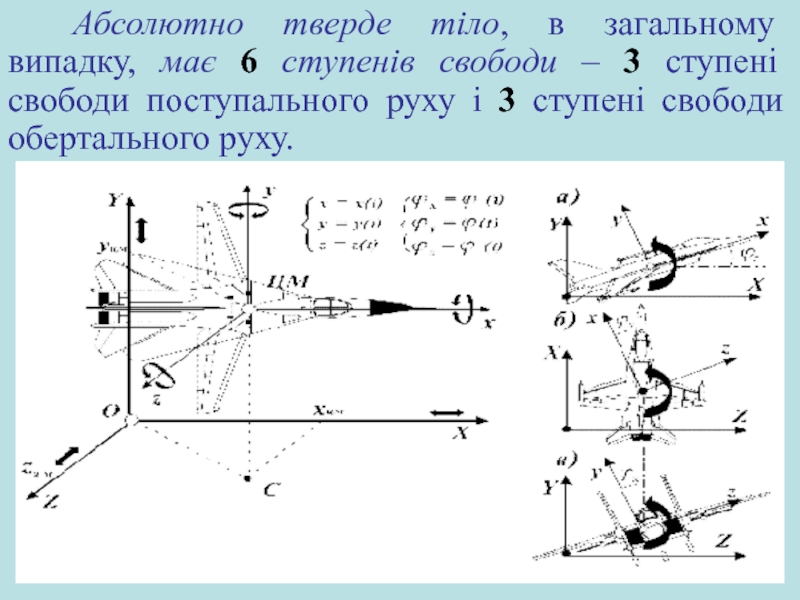
Слайд 4Абсолютно тверде тіло, в загальному випадку, має 6 ступенів свободи
– 3 ступені свободи поступального руху і 3 ступені свободи
обертального руху.
Слайд 5Якщо тіло не абсолютно тверде і його частини можуть зміщуватись
одна відносно одної, то вводять ще додаткові ступені вільності коливального
руху.
Слайд 62. Момент сили. Момент інерції
Момент інерції – скалярна фізична величина,
що є мірою інерції обертального руху тіл (аналогічно масі при
поступальному русі тіла).
Слайд 7Тверде тіло, що обертається навколо певної осі можна розглядати як
систему з нескінченної кількості матеріальних точок, кожна з масою mi,
відстані від кожної точки до осі обертання дорівнюють ri.
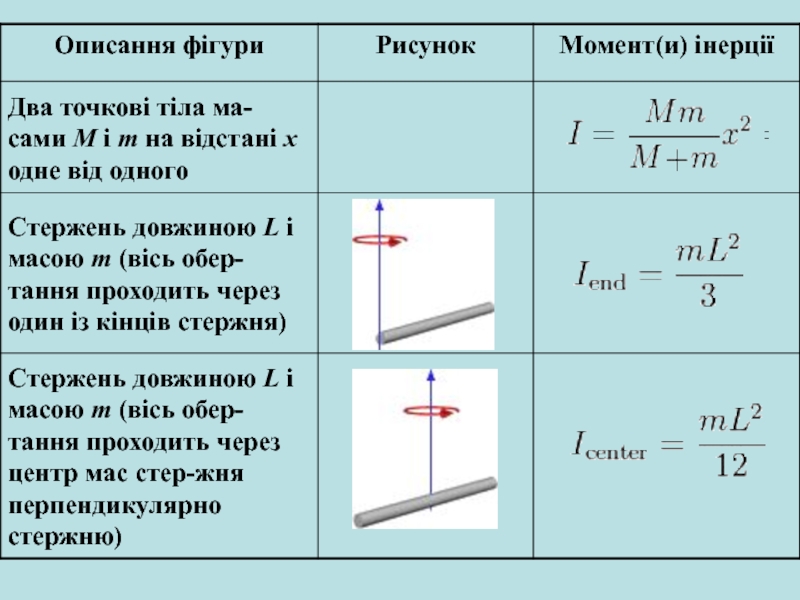
Момент інерції точки дорівнює
Слайд 8Моментом інерції тіла (системи точок) відносно осі обертання називають скалярну
фізичну величину, чисельно рівну сумі добутків мас п матеріальних точок
системи на квадрат їх відстаней до осі вибраної
За умов безперервного розподілення маси в тілі, момент інерції:
де dm – елемент маси, який визначають через просторовий розподіл густини ρ в тілі.
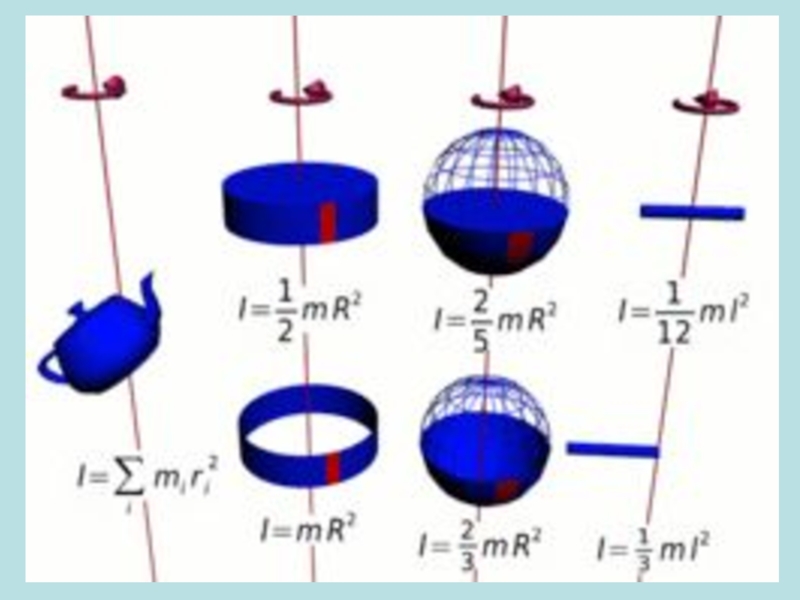
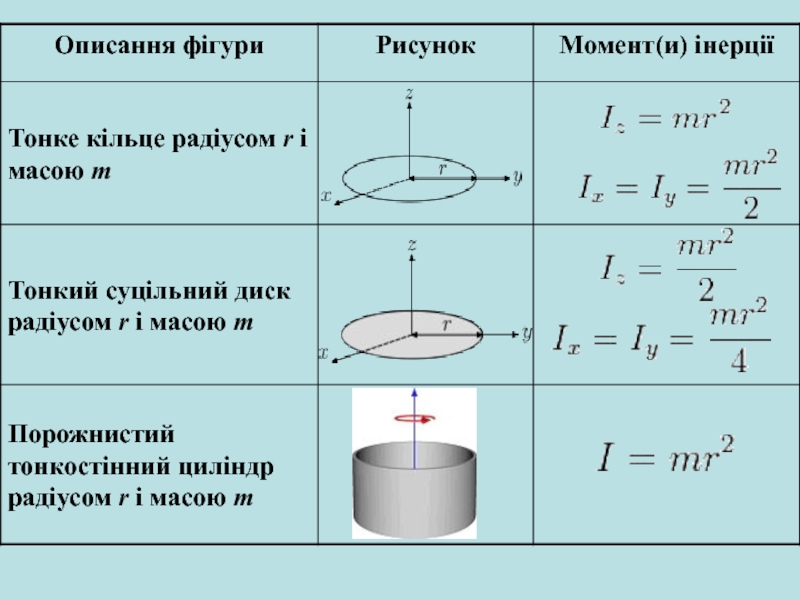
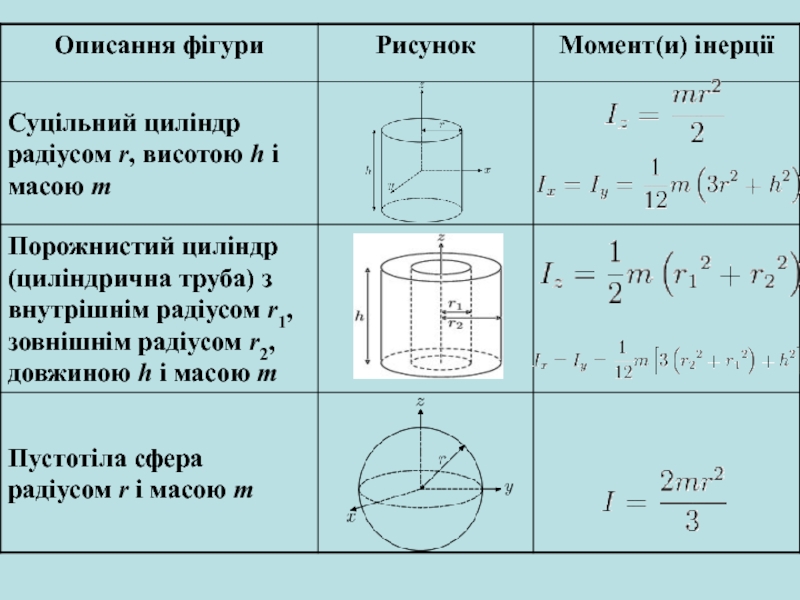
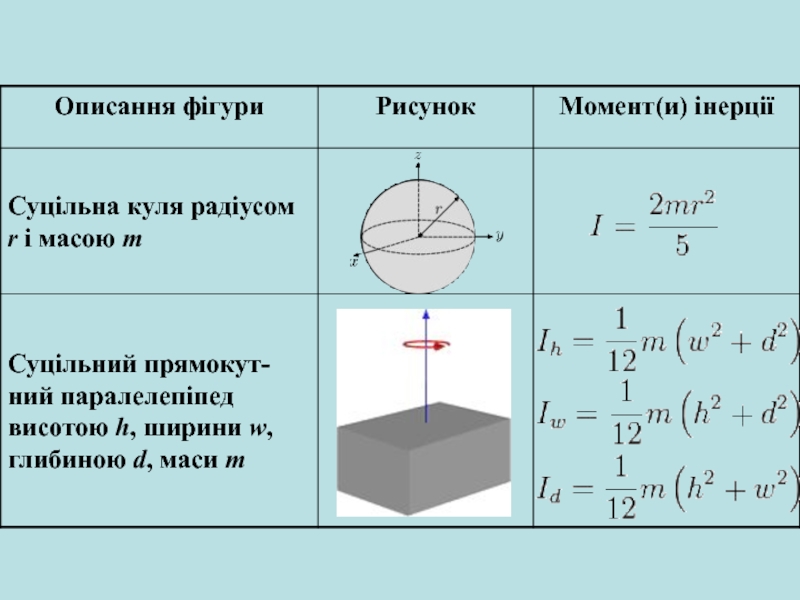
Слайд 9В загальному випадку, значення моменту інерції тіла залежить від його
форми та розподілу маси в об'ємі: чим більше маси сконцентровано
далі від центру мас тіла, тим більшим є його момент інерції. Також значення моменту інерції тіла залежить від обраної осі обертання.
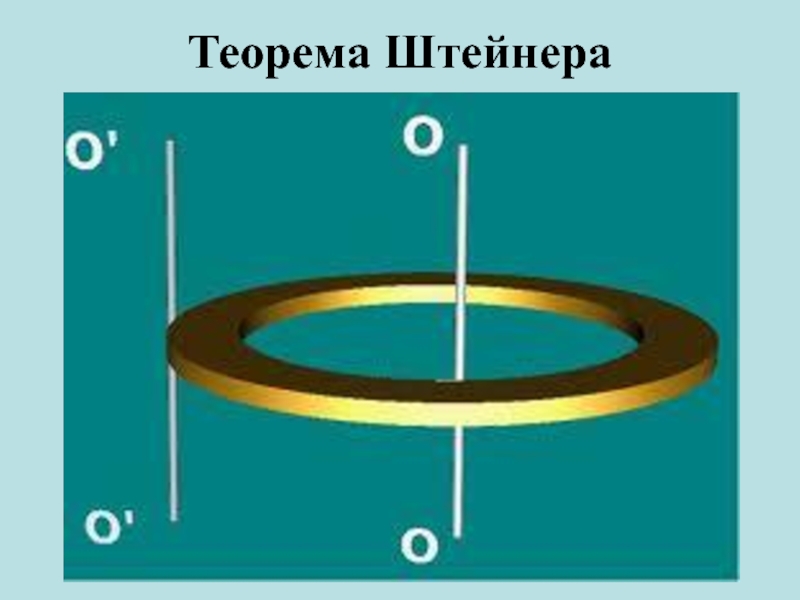
Слайд 11Якщо відомо момент інерції тіла відносно осі, що проходить через
його центр мас, то момент інерції відносно іншої довільної паралельної
їй осі, можна визначити за теоремою Штейнера (теоремою Гюйгенса-Штейнера),
момент інерції тіла І відносно довільної осі дорівнює сумі моменту інерції цього тіла І0 відносно осі, що проходить через центр мас тіла паралельно до осі, що розглядається, і добутку маси тіла m на квадрат відстані d між осями:
Слайд 17Будь-яке тіло завжди можна розглядати як систему з n матеріальних
точок, причому маса m тіла дорівнює сумі мас усіх цих
точок:
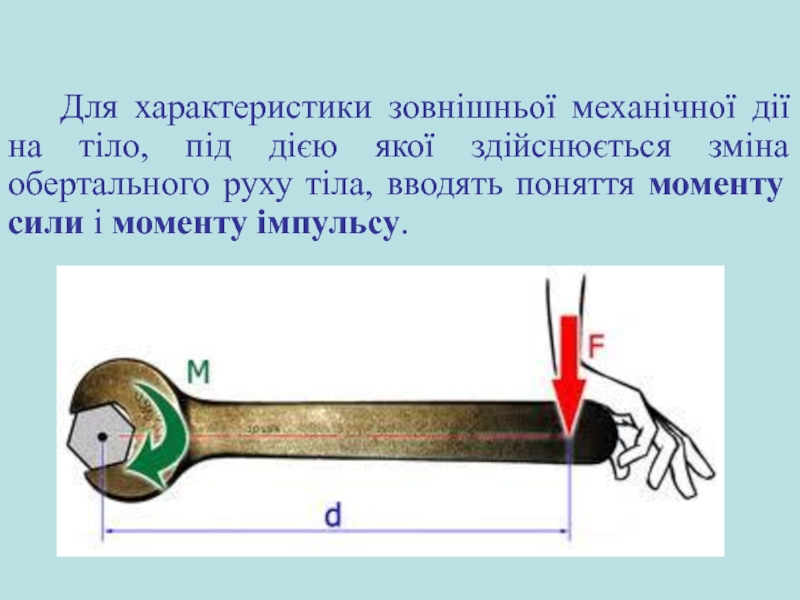
Слайд 18 Для характеристики зовнішньої механічної дії на тіло, під дією
якої здійснюється зміна обертального руху тіла, вводять поняття моменту сили
і моменту імпульсу.
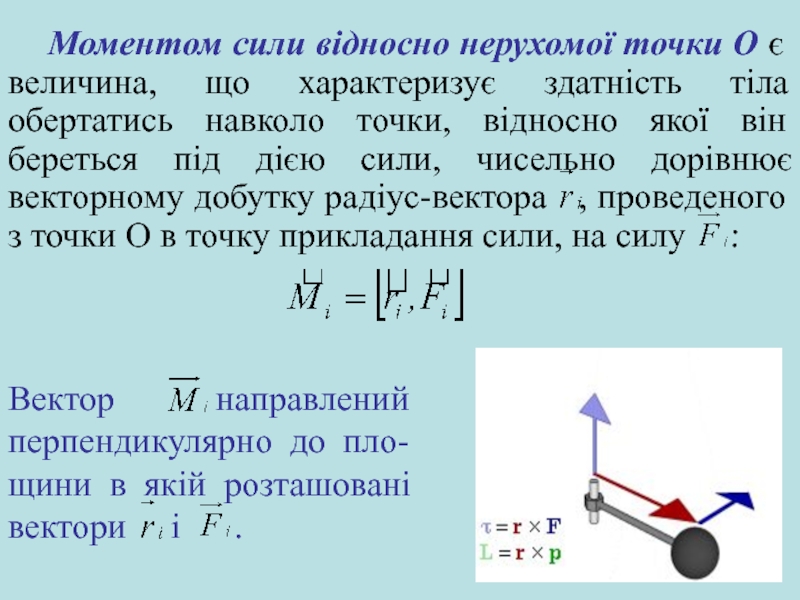
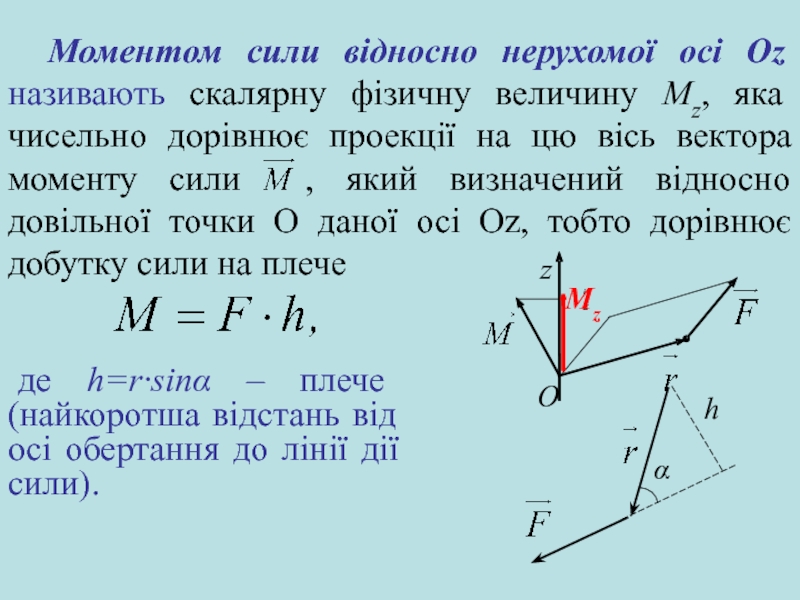
Слайд 20Моментом сили відносно нерухомої осі Оz називають скалярну фізичну величину
Mz, яка чисельно дорівнює проекції на цю вісь вектора
моменту сили , який визначений відносно довільної точки О даної осі Oz, тобто дорівнює добутку сили на плече
де h=r·sinα – плече (найкоротша відстань від осі обертання до лінії дії сили).
Слайд 223. Закон динаміки обертального руху
Оскільки момент сили рівний M=F·r·sinα, то
при α=π/2 він дорівнюватиме
M=F·r або M=ma·r.
Замінимо α кутовим
прискоренням β:
α=β·r.
Тоді M=mβ·r2, або, враховуючи, що mr2=I,
M=Iβ.
Слайд 23Основний закон динаміки обертального руху: результуючий момент зовнішніх сил призводить
до зміни стану обертального руху тіла, тобто зумовлює зміну його
кутової швидкості.
Слайд 244. Умови рівноваги твердого тіла. Центр ваги. Види рівноваги
Умови рівноваги
тіл або систем тіл під дією прикладених сил або моментів
сил вивчає статика ( від грец. στατός – “нерухомий”).
Слайд 25Більш детально умови рівноваги тіл у будів-ництві вивчають у курсах
“Будівельна механіка” – вивчає стійкість будівельних конструкцій та “Будівельні машини
та обладнання” – вивчає
стійкість будівельних машин та обладнання під дією навантажень, що створюють моменти сил, здатні перекинути об’єкт
Слайд 26До основних навантажень відносять – піднімання, захвачування або перевезення вантажів,
до додаткових – інерційні навантаження, що вини-кають в момент пуску,
прискорення або гальмуван-ня механізмів; центробіжні навантаження, що ви-никають при повороті або нахилі частин механіз-мів; вітровий тиск або тиск атмосферних опадів тощо).
Слайд 27Тіло буде залишатися в стані спокою, якщо немає причин, що
викликають його рух. Згідно основних рівнянь динаміки поступального і обертального
рухів це можливо за виконання умов:
1) сума всіх зовнішніх сил, прикладених до тіла, має дорівнювати нулю:
2) сума моментів усіх сил, що діють на тіло, відносно будь-якої точки має дорівнювати нулю:
Слайд 28Для тіла, що має нерухому вісь обертання, можливі три види
рівноваги:
1) стійка рівновага – рівновага, за якої при малих
відхиленнях тіла від цього стану виникають сили чи моменти сил, що намагаються повернути тіло в рівноважний стан;
Слайд 29Для тіла, що має нерухому вісь обертання, можливі три види
рівноваги:
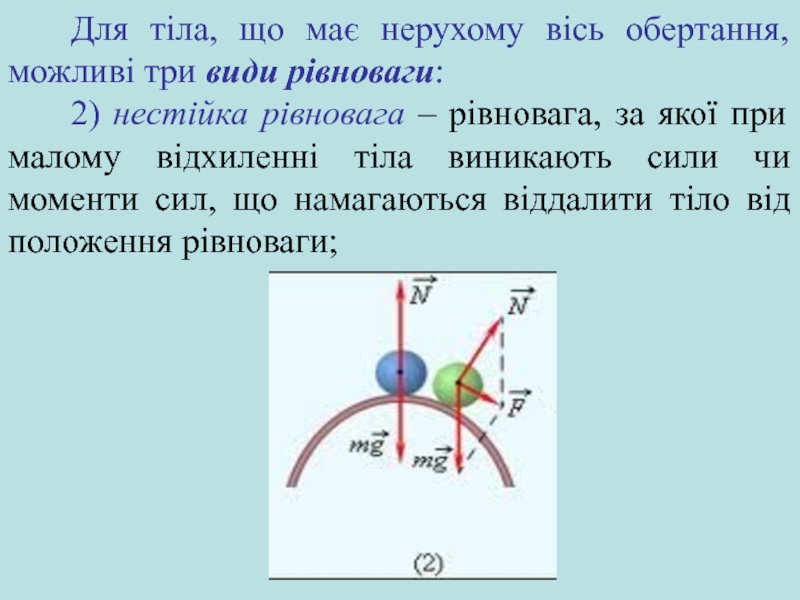
2) нестійка рівновага – рівновага, за якої при малому
відхиленні тіла виникають сили чи моменти сил, що намагаються віддалити тіло від положення рівноваги;
Слайд 30Для тіла, що має нерухому вісь обертання, можливі три види
рівноваги:
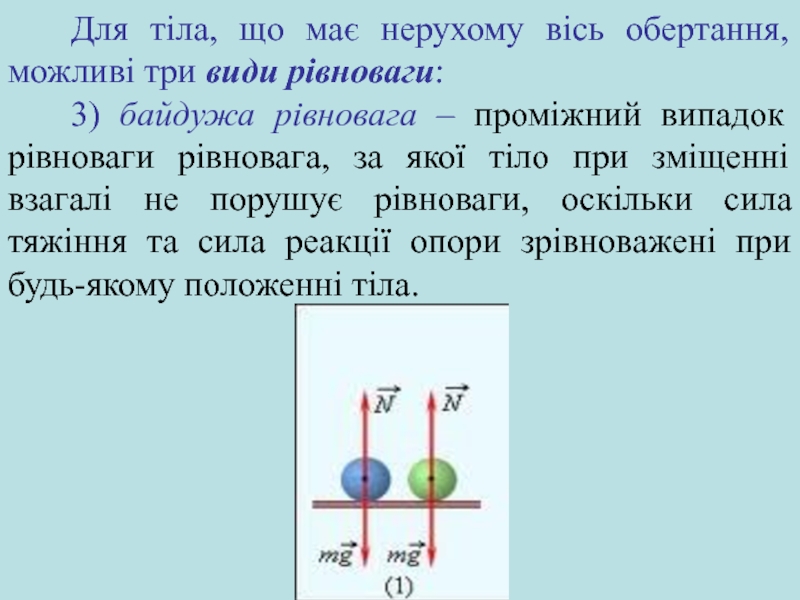
3) байдужа рівновага – проміжний випадок рівноваги рівновага, за
якої тіло при зміщенні взагалі не порушує рівноваги, оскільки сила тяжіння та сила реакції опори зрівноважені при будь-якому положенні тіла.
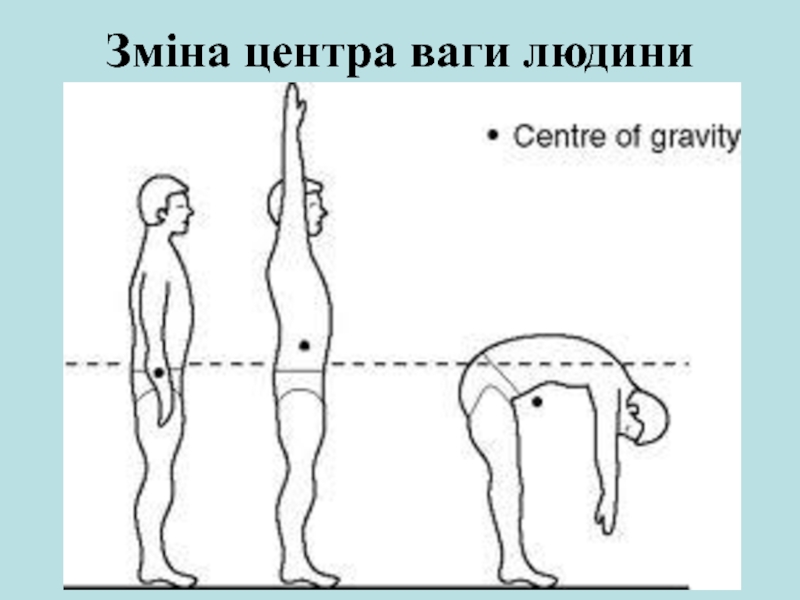
Слайд 32 Слід вибрати момент, коли центр ваги противника не знаходиться
у стані стійкої рівноваги
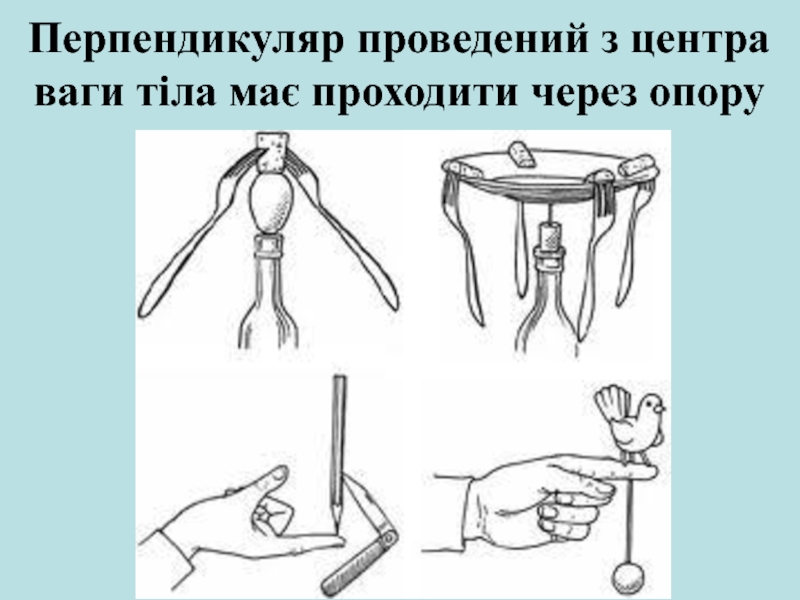
Слайд 33Перпендикуляр проведений з центра ваги тіла має проходити через опору
Слайд 36Якщо рівновага стійка, центр тяжіння кулі займає найнижче положення відносно
опори. Якщо рівновага нестійка, центр тяжіння кулі займає найвище положення
відносно опори. Тому положення стійкої рівноваги характеризується мінімальною потенціальною енергією.
Слайд 37Особливим випадком є рівновага тіла на опорі. У цьому випадку
сила реакції опори прикладена не до однієї точки, а розподілена
по площі основи тіла. Тіло знаходиться в рівновазі, якщо вертикальна лінія, проведена через центр мас тіла, проходить через площу опори, тобто всередині контуру, утвореного лініями, що з’єднують точки опори. Якщо ж ця лінія не перетинає площу опори, то тіло перекидається.
Слайд 38З умови рівноваги тіла, яке опирається на декілька точок, стає
зрозумілим, чому підйомні крани завжди обладнуються тяжкою противагою для підвищення
їхньої стійкості проти перекидання.
Дякуючи противазі спільний центр тяжіння, крана, вантажу та противаги не виступає за прямокутник, обмежений точками опори коліс, навіть тоді, коли кран піднімає тяжкий вантаж. На кранах з поворотною баштою (рис. а) противагу підвішують на поворотній платформі, на кранах з неповоротною баштою (рис. б) – на противажній консолі.
Противага
Слайд 395. Момент імпульсу. Закон збереження моменту імпульсу.
Для характеристики зовнішньої
механічної дії на тіло, під дією якої здійснюється зміна обер-тального
руху тіла, вводять поняття моменту сили і моменту імпульсу.
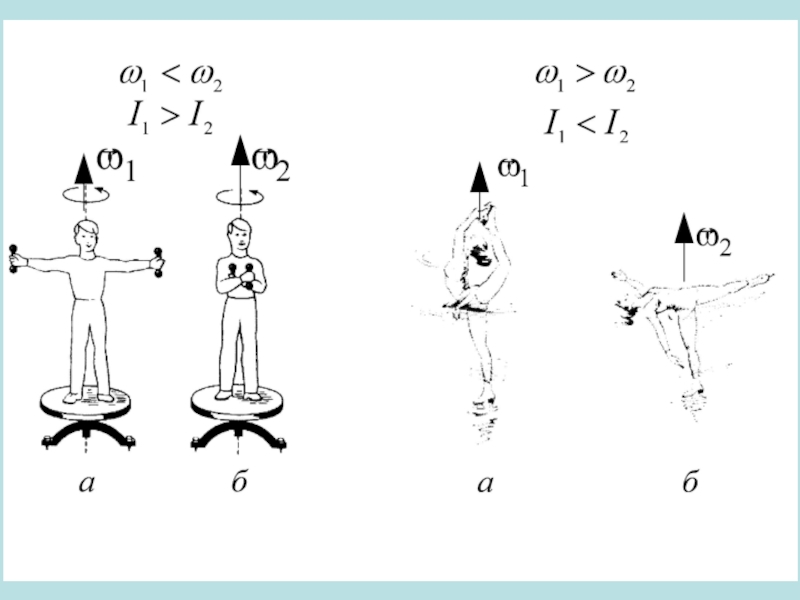
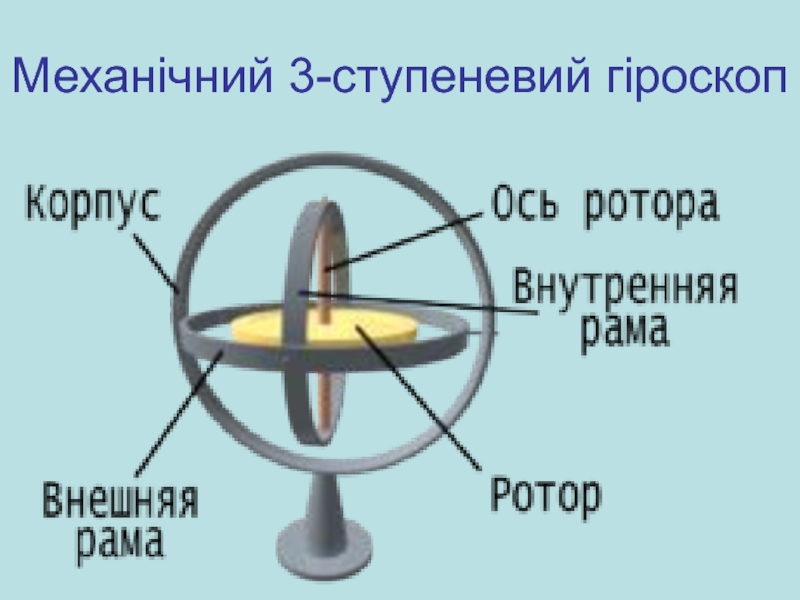
Слайд 47Механічний 3-ступеневий гіроскоп
Слайд 57Інерціальна навігаційна система для судів або літаків
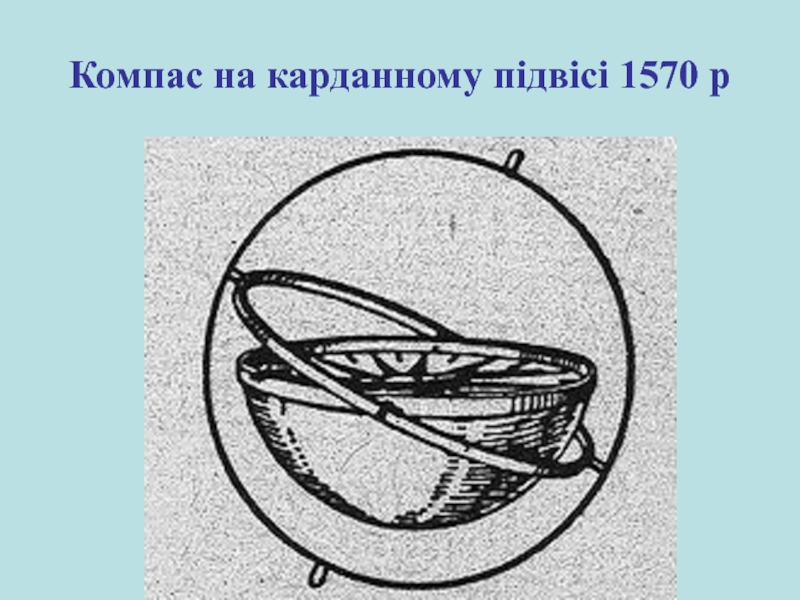
Слайд 58Компас на карданному підвісі 1570 р
Слайд 59Радіокерівний гелікоптер з гіроскопом, який відповідає за стабільність апарату у
повітрі, а також при злеті і посадці
Слайд 62
Ступені свободи руху абсолютно твердого тіла
Момент сили. Момент
інерції
Закон динаміки обертального руху
Умови рівноваги твердого тіла. Центр ваги. Види
рівноваги
Момент імпульсу. Закон збереження моменту імпульсу
Уявлення про гіроскопи
Лекція № 4.
Динаміка обертального руху