Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сумський державний університет Кафедра військової підготовки
Содержание
- 1. Сумський державний університет Кафедра військової підготовки
- 2. Навчальні питанняКосмічні швидкості та траєкторії руху ракет
- 3. Перше питанняКосмічні швидкості та траєкторії руху ракет у центральному полі тяжіння.
- 4. Траєкторія ( від латинського trajectories – тобто
- 5. Форма траєкторії ракети залежить від деяких початкових
- 6. При розгляді форми траєкторії польоту ракети у
- 7. Основною умовою руху ракет у центральному полі
- 8. Рух ракет відбувається у площині, яка проходить
- 9. Крім того, у визначеній площині, рух ракет
- 10. У залежності від
- 11. Відповідно до цього,
- 12. Слайд 12
- 13. Гравітаційна сила визначається законом всесвітнього тяжіння Ньютона,
- 14. Ця сила визначається дослідним шляхом і дорівнює
- 15. Відцентрова сила інерції характеризує зусилля тіла на відрив від Землі, та визначається за формулою:
- 16. Слайд 16
- 17. Як вже було відмічено, щоб ракета не
- 18. Швидкість польоту ракети , що визначається за формулою, називається першою космічною швидкістю.
- 19. Ця швидкість визначає умови існування штучних супутників
- 20. Тому, першу космічну швидкість розраховують для висоти,
- 21. Із формули можливо помітити, що при збільшені
- 22. Так, як гравітаційна сила є
- 23. Прискорення сили тяжіння (вільного падіння) на поверхні
- 24. Як бачимо, при збільшені відстані від поверхні
- 25. Еліптична траєкторія (орбіта) в прямокутній системі координат
- 26. Точка О називається центром еліпса і
- 27. Відношення половини фокусної відстані (c ) до
- 28. Параболічна траєкторія Еліптична орбіта, що має апогей
- 29. Для реалізації параболічної траєкторії необхідна така швидкість
- 30. Потенціальну енергію вимірюють роботою
- 31. Гіперболічна траєкторія Якщо швидкість тіла перевищує значення
- 32. Балістична траєкторія - це траєкторія польоту, рух
- 33. Балістика – це наука, яка займається законами
- 34. Балістична ракета – це літальний апарат, що
- 35. Слайд 35
- 36. Активна ділянка траєкторії (АДТ) – це ділянка
- 37. Пасивна ділянка траєкторії (ПДТ) – це ділянка
- 38. Основними характеристиками (елементами) балістичної траєкторії польоту є:-
- 39. Друге питанняФормула Ціолковського щодо ідеальної швидкості руху ракети
- 40. К.Е.Ціолковський своєю відомою формулою для ідеальної швидкості
- 41. Ідеальною швидкістю (швидкістю Ціолковського ) називають максимальну
- 42. Ціолковський отримав формулу щодо визначення ідеальної швидкості,
- 43. Слайд 43
- 44. Після відповідних математичних перетворень отримаємо залежність
- 45. Дійсна швидкість одноступеневої ракети , в наслідок
- 46. Враховуючи цю залежність, можливо отримати формулу для
- 47. Скачать презентанцию
Навчальні питанняКосмічні швидкості та траєкторії руху ракет у центральному полі тяжіння.Формула Ціолковського щодо ідеальної швидкості руху ракет.Загальні відомості щодо траєкторії польоту балістичної ракети.
Слайды и текст этой презентации
Слайд 1Сумський державний університет
Кафедра військової підготовки
Лекція №2 з предмету “Конструкція ракет”
Тема
2. Основи теорії польоту ракет.
ракет.Слайд 2Навчальні питання
Космічні швидкості та траєкторії руху ракет у центральному полі
тяжіння.
Формула Ціолковського щодо ідеальної швидкості руху ракет.
Загальні відомості щодо траєкторії
польоту балістичної ракети.Слайд 4Траєкторія ( від латинського trajectories – тобто та, що відноситься
до переміщення ) – це безперервна просторова лінія, яку описує
центр мас ракети у польоті відносно вибраної системи координат.Слайд 5Форма траєкторії ракети залежить від деяких початкових умов польоту, а
саме: від величини і напрямку вектора її швидкості та координат
ракети в момент вимкнення двигуна.Слайд 6При розгляді форми траєкторії польоту ракети у даному питанні заняття,
будемо вважати, що її рух відбувається під дією сили Земного
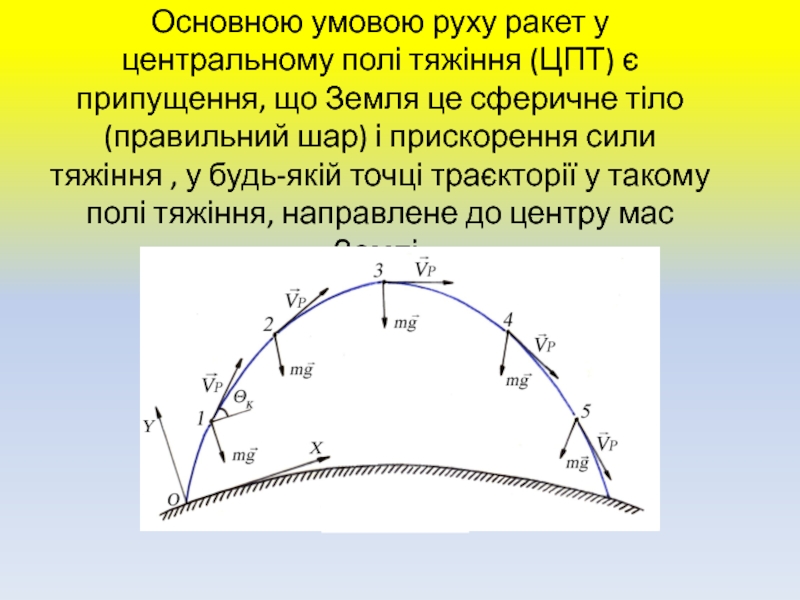
тяжіння і що це тяжіння є центральним (центральне поле тяжіння).Слайд 7Основною умовою руху ракет у центральному полі тяжіння (ЦПТ) є
припущення, що Земля це сферичне тіло (правильний шар) і прискорення
сили тяжіння , у будь-якій точці траєкторії у такому полі тяжіння, направлене до центру мас Землі.Слайд 8Рух ракет відбувається у площині, яка проходить через центр Землі
(люба траєкторія руху у центральному полі тяжіння (ЦПТ) завжди лежить
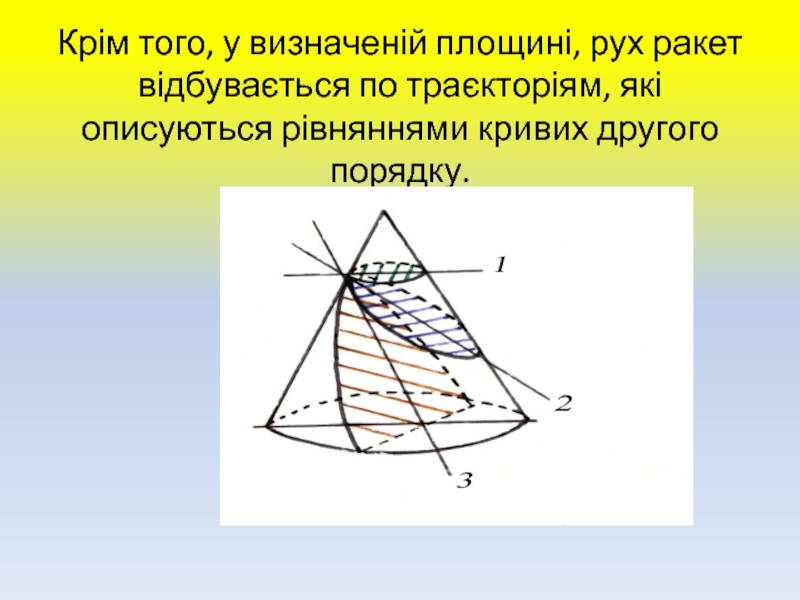
у площині, що проходить через центр тяжіння).Слайд 9Крім того, у визначеній площині, рух ракет відбувається по траєкторіям,
які описуються рівняннями кривих другого порядку.
Слайд 10 У залежності від нахилу секцій розтинаючої
площини, конічними перетинами можуть бути :
1 – коло;
2 – еліпс;
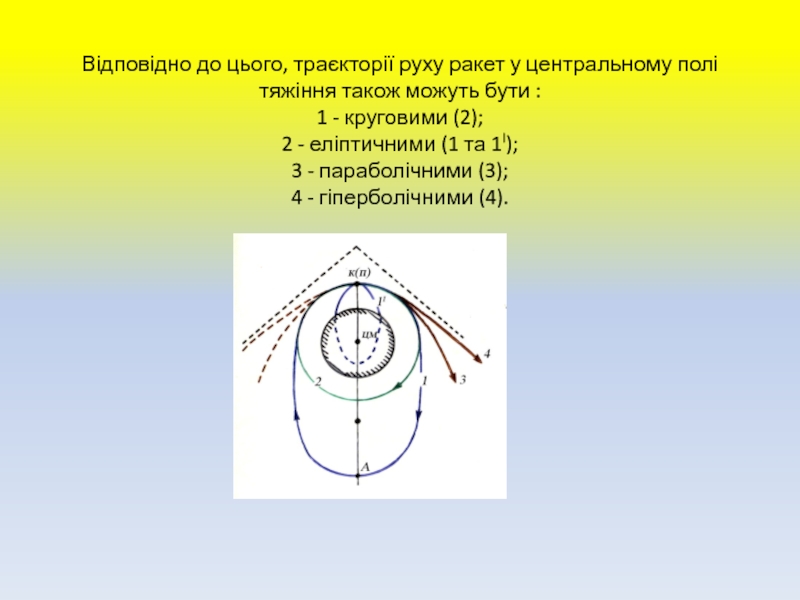
3 – парабола (гіпербола).Слайд 11 Відповідно до цього, траєкторії руху ракет у центральному полі тяжіння
також можуть бути : 1 - круговими (2); 2 - еліптичними (1
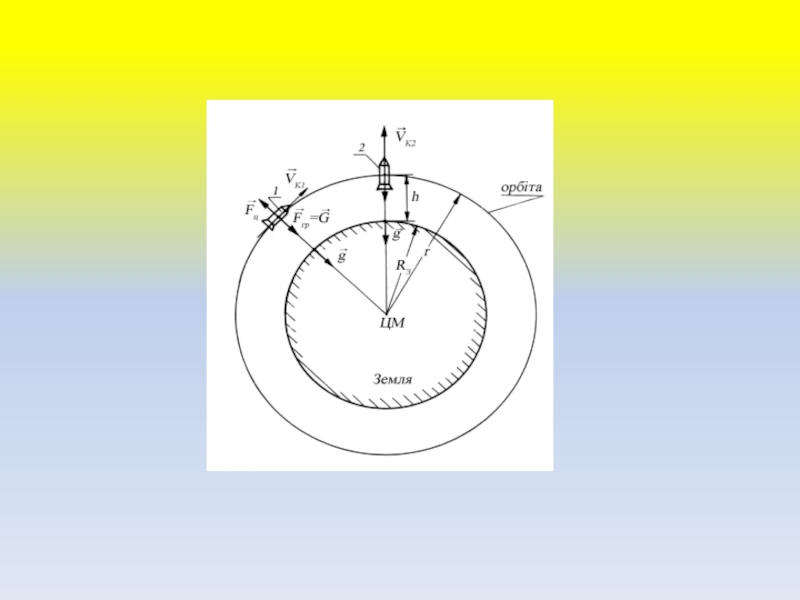
та 1I); 3 - параболічними (3); 4 - гіперболічними (4).Слайд 12 Кругова
траєкторія
Для польоту будь-якого тіла по траєкторії кола, необхідно щоб
у всіх точках такої траєкторії, кут її нахилу до поверхні Землі мав нульове значення. Крім того, у всіх точках цієї траєкторії, сила притягання до Землі (гравітаційна сила) повинна бути урівноваженою відцентровою силою Fц.Слайд 13Гравітаційна сила визначається законом всесвітнього тяжіння Ньютона, який звучить наступним
чином: усі тіла притягуються одне до одного з силою, що
пропорційна добутку їх мас та зворотно пропорційна квадрату відстані між ними.Взагалі, під гравітацією розуміють – взаємне притягання, яке діє на всі тіла у Всесвіті.
Слайд 14Ця сила визначається дослідним шляхом і дорівнює силі взаємного тяжіння
між двома масами.
,де f - гравітаційна стала (стала тяжіння);
m– маса ракети [кг];
M [кг] – маса Землі;
– радіус орбіти (траєкторії) [м].
Слайд 15Відцентрова сила інерції характеризує зусилля тіла на відрив від Землі,
та визначається за формулою:
Слайд 17Як вже було відмічено, щоб ракета не наближалась і не
віддалялась від Землі, необхідно виконати умову , із якої можливо
отримати формулу швидкості, яку необхідно надати ракеті для її виходу на траєкторію кола:,
де – постійний коефіцієнт (гравітаційний параметр планети).
Слайд 18Швидкість польоту ракети , що визначається за формулою, називається першою
космічною швидкістю.
Слайд 19Ця швидкість визначає умови існування штучних супутників Землі (ШСЗ) та
характеризує гравітаційне поле планети. У поверхні Землі (при
– цю швидкість називають нульовою круговою швидкістю для Землі. Але, кругова траєкторія на рівні земної поверхні при фактично нездійсненна.Слайд 20Тому, першу космічну швидкість розраховують для висоти, де ШСЗ здатен
здійснити хоча б один оборот. Як правило, за першу космічну
швидкість приймають кругову швидкість на висоті 200 км над поверхнею Землі, в цьому випадку V1=7,79 км/сек.Слайд 21Із формули можливо помітити, що при збільшені радіусу траєкторії польоту,
значення потрібної кругової швидкості зменшується. Для з’ясування причини цього явища
необхідно розглянути таку важливу характеристику гравітаційного поля, як прискорення вільного падіння .Слайд 22Так, як гравітаційна сила є також силою тяжіння
, що визначається за формулою
, то порівнюючи , отримаємо:
Слайд 23Прискорення сили тяжіння (вільного падіння) на поверхні Землі визначається для
h=0 як:
тоді для h=200 км,
Слайд 24Як бачимо, при збільшені відстані від поверхні Землі, значення прискорення
сили тяжіння - зменшується, що в свою чергу приводить до
зменшення потрібного значення кругової швидкості.Слайд 26
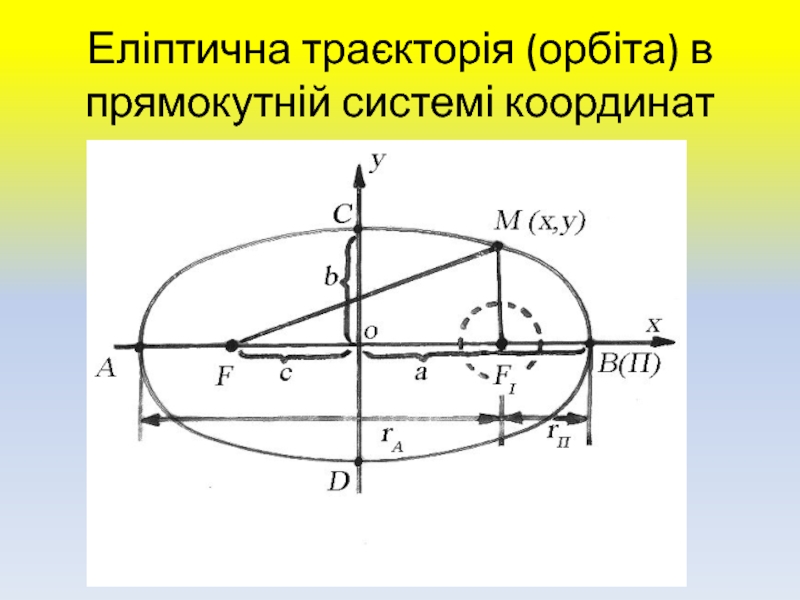
Точка О називається центром еліпса і співпадає з початком
координат. Точки A,B,C,D називають вершинами еліпсу.
Відрізок АВ довжиною має
назву велика вісь еліпса ( a – велика напіввісь).Відрізок CD довжиною 2b називають мала вісь еліпсу (b– мала напіввісь). Точки F i F1 , які розташовані на великій вісі еліпсу на відстані
(c ), від його центру, називають фокусами еліпсу.
Слайд 27Відношення половини фокусної відстані (c ) до великої полувісі (
a) називають ексцентриситетом еліпсу:
Ексцентриситет еліпсу вказує на ступінь його відхилення від кола. Так, якщо c=0, то і e=0 (фокуси F і F1 співпадають з центром еліпсу і траєкторія становиться круговою). Виходячи з цього, траєкторію кола можливо розглядати, як частковий випадок еліпса з ексцентриситетом, що дорівнює нулю.
Слайд 28Параболічна траєкторія
Еліптична орбіта, що має апогей у нескінченності вже не
є еліпсом. Рухаючись по цій траєкторії, ракета нескінченно віддаляється від
центру тяжіння та описує розімкнуту лінію – параболу.Слайд 29Для реалізації параболічної траєкторії необхідна така швидкість ,
яка зможе забезпечити подолання сили земного тяжіння. Цю швидкість називають
другою космічною швидкістю, або швидкістю звільнення.Другу космічну швидкість можливо отримати, якщо порівняти потенціальну і кінетичну енергію ракети в точці вимкнення двигуна ракети.
Слайд 30Потенціальну енергію вимірюють роботою
або
Кінетичну енергію
визначають: .Порівнявши кінетичну та потенціальну енергію ракети , знайдемо другу космічну швидкість:
Слайд 31Гіперболічна траєкторія
Якщо швидкість тіла перевищує значення , тобто
коли траєкторія має вид
гіперболи.На великій відстані від центру тяжіння гіперболічну траєкторію можливо рахувати прямолінійною.
Слайд 32Балістична траєкторія - це траєкторія польоту, рух по якій здійснюється
тільки під дією сили тяжіння.
Саме слово балістика походить з грецької
мови та співзвучно слову – “ballö” - кидаю. Слайд 33Балістика – це наука, яка займається законами руху ракет та
артилерійських снарядів. Розрізняють поняття внутрішньої та зовнішньої балістики.
Внутрішня балістика розглядає,
як правило, рух артилерійських снарядів в каналі ствола гармати.Зовнішня балістика, займається вивченням польоту ракет та снарядів після припинення їх силової взаємодії з пусковою установкою (гарматою).
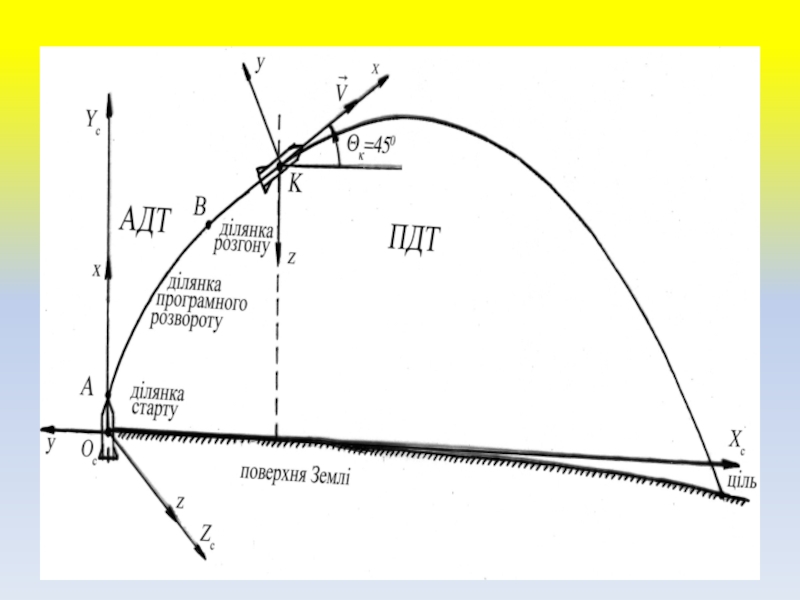
Слайд 34Балістична ракета – це літальний апарат, що частину свого шляху
проходить по балістичній траєкторії. Траєкторія польоту балістичної ракети з моменту
старту до моменту зустрічі з ціллю, завжди поділяється на дві ділянки : активну і пасивну.Слайд 36Активна ділянка траєкторії (АДТ) – це ділянка траєкторії, на якій
ракета рухається за рахунок сили тяги, що утворюється її двигуном.
Ракета на цій ділянці рухається з прискоренням та накопичує кінетичну енергію.Слайд 37Пасивна ділянка траєкторії (ПДТ) – це ділянка вільного польоту ракети
(з вимкнутим двигуном) за рахунок накопиченої на АДТ кінетичної енергії.
Слайд 38Основними характеристиками (елементами) балістичної траєкторії польоту є:
- дальність польоту ракети
( L );
- висота траєкторії ( H );
- час польоту
( tп );- кут кидання ( ).
Слайд 40К.Е.Ціолковський своєю відомою формулою для ідеальної швидкості ракети, відповів на
питання: - за допомогою яких технічних пристроїв можливе досягнення космічних
швидкостей і виведення корисного вантажу (бойової частини) на будь-яку із розглянутих нами траєкторій.Слайд 41Ідеальною швидкістю (швидкістю Ціолковського ) називають максимальну швидкість, яку може
отримати ракета, яка здійснює вертикальний політ у безповітряному просторі, при
відсутності сили тяжіння після повного витрачення ракетного палива.Слайд 42Ціолковський отримав формулу щодо визначення ідеальної швидкості, скориставшись рівнянням Мещерського,
для поступального руху тіл змінної маси:
Так, як була визначена ідеальна
швидкість (при ідеальних умовах), то рівняння Мещерського, без врахування прийме наступний вигляд:Слайд 43
,
де - тяга ракетного двигуна:
,
де – питомий імпульс тяги [м/с];
- масова витрата палива [кг/с].