Слайд 1Сводка и группировка статистических данных
Понятие. Задачи. Этапы. Виды.
Слайд 2Статистическая сводка -
комплекс последовательных операций по первичной обработке данных с целью
выявления типичных черт и закономерностей, присущих изучаемому явлению.
научно-организованная обработка
материалов наблюдения, включающая подсчет групповых и общих итогов, получение производных показателей (средних, относительных величин), систематизацию, группировку данных и составление таблиц и графиков
систематизация единичных фактов, позволяющая перейти к обобщающим показателям, относящимся по всей изучаемой совокупности и ее частям и осуществить анализ и прогнозирование изучаемых явлений и процессов.
Слайд 3Задача сводки
дать характеристику объекту исследования с помощью системы
статистических показателей, выявить и измерить его существенные черты и особенности:
определение
групп и подгрупп;
определение системы показателей;
определение видов таблиц.
Слайд 4Этапы сводки стат.данных:
1 этап: осуществляется систематизация, группировка материалов, собранных при
наблюдении.
2 этап: уточняется предусмотренная планом система показателей, с помощью
которых количественно характеризуются свойства и особенности изучаемого предмета.
3 этап: исчисляются сами показатели; обобщенные данные представляется в таблицах, статистических рядах, графиках, диаграммах.
Слайд 5Статистическая сводка:
Простая сводка - это операция по подсчету общих итогов
по совокупности единиц наблюдения.
Сложная сводка - это комплекс операций, включающих
группировку единиц наблюдения, подсчет итогов по каждой группе и по всему объекту и представление результатов группировки и сводки в виде статистических таблиц.
Слайд 6Подлежащее сводки составляют группы или части, на которые разбивается совокупность.
Сказуемое
сводки составляют показатели, характеризующие каждую группу и совокупность в целом.
Статистическая
сводка:
Слайд 7Группировка -
это метод, при котором вся исследуемая совокупность разделяется на группы по какому-то
существенному признаку.
Слайд 8Функции группировки:
выделение социально-экономических типов явлений;
изучение структуры и структурных сдвигов, происходящих
в социально-экономических явлениях;
анализ взаимосвязей между явлениями;
выявление влияния отдельных единиц на
средние итоговые показатели
Слайд 9Категории метода группировки:
Группировочный признак
Интервал группировки
Число групп
Слайд 101. Группировочный признак (основание группировки) -
признак, по которому осуществляется группировка
(по которому происходит объединение отдельных единиц совокупности в однородные группы)
По
количеству группировочных признаков, выделяют: простую (монотетическую) группировку (если для построения группировки используется один группировочный признак); сложную, многомерную (политетическую) группировку (если для построения группировки используется несколько группировочных признаков). Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в комбинации
Слайд 11В зависимости от решаемых задач различают:
Типологическую группировку - разделение исследуемой совокупности
на однородные группы.
Структурную группировку - в которой происходит разделение однородной
совокупности на группы, характеризующие ее структуру по какому-то варьирующему признаку. Изменение структуры изучаемых явлений - структурные сдвиги.
Аналитическую (факторную) группировку -позволяет выявить взаимосвязи между изучаемыми явлениями и их признаками (показатели: обобщающий (результативный) и факторные)
Слайд 122. Интервал группировки - значение варьирующего признака, лежащее в определенных
пределах
Нижняя граница - значение наименьшего признака в интервале.
Верхняя граница
- наибольшее значение в интервале.
Величина (ширина) интервала - разница между верхней и нижней границами.
Слайд 13Интервалы бывают:
равные, когда разность между максимальным и минимальным значениями в
каждом из интервалов одинакова или значение количественного признака внутри совокупности
изменяется равномерно;
неравные, когда значения признака варьируют неравномерно и в значительных размерах (прогрессивно возрастающие, прогрессивно - убывающие, произвольные и специализированные);
открытые, у которых указана только одна граница, либо верхняя, либо нижняя;
закрытые, когда имеются и нижняя, и верхняя границы.
Слайд 14Величина равных интервалов определяется по формуле:
i = (Xmax-Xmin)/n, или i
= R/n,
где R – размах вариации = Xmax-Xmin
i— величина
интервала
Xmax - максимальное значение признака в совокупности
Xmin — минимальное значение признака в совокупности
n— число групп
Правила округления интервалов:
Если интервал имеет один знак ДО запятой, то полученное значение округляется до десятых (0,88 = 0,9; 8,715 = 8,7)
Если величина интервала имеет два знака ДО запятой, то полученное значение округляется до целых (11,11 = 11; 29,98 = 30)
Если интервал трех, четырех и более значимое число, то интервал принимают кратным 50 или 100 (h=246≈250)
Слайд 15Величина неравных интервалов определяется по формулам:
Величина интервалов, изменяющихся в арифметической
прогрессии:
hi+1= hi +a, где
а - константа, которая будет
положительной при прогрессивно возрастающих интервалах и отрицательной при прогрессивно убывающих;
Величина интервалов, изменяющихся в геометической прогрессии:
hi+1= hi *q, где
q - положительная константа, которая при прогрессивно возрастающих интервалах больше 1, а при прогрессивно убывающих интервалах меньше 1.
Слайд 163. Определение числа групп n, при N единицах совокупности
(формула
Стерджесса)
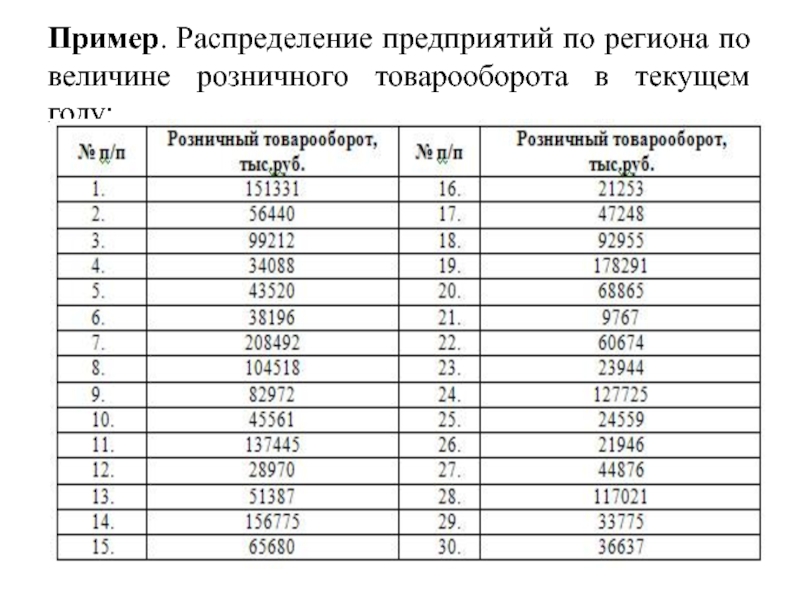
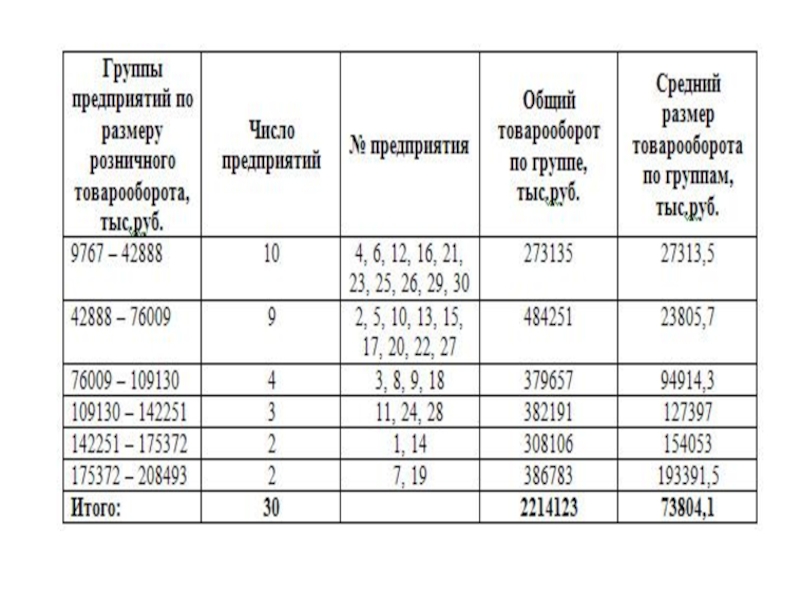
Слайд 17Пример. Распределение предприятий по региона по величине розничного товарооборота в
текущем году:
Слайд 18lg30=1,477121254719
Величину интервала i=h определяют по следующей формуле:
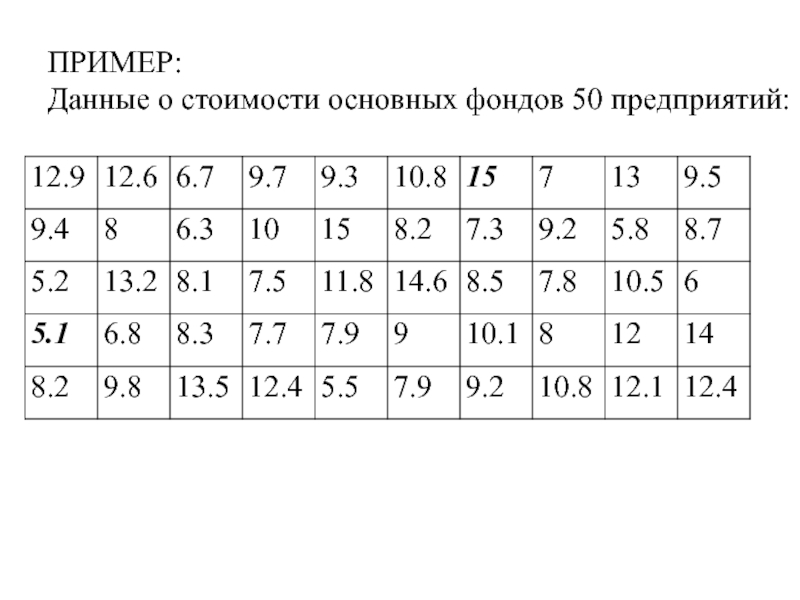
Слайд 20ПРИМЕР:
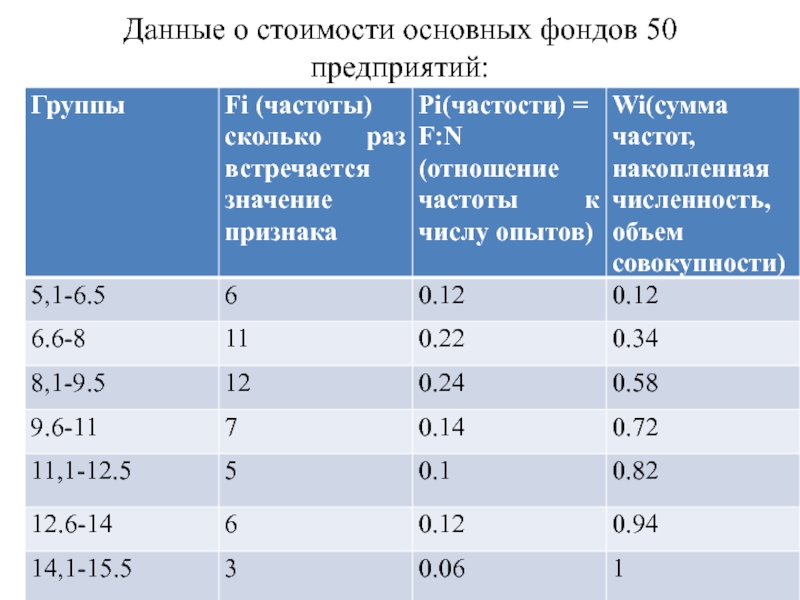
Данные о стоимости основных фондов 50 предприятий:
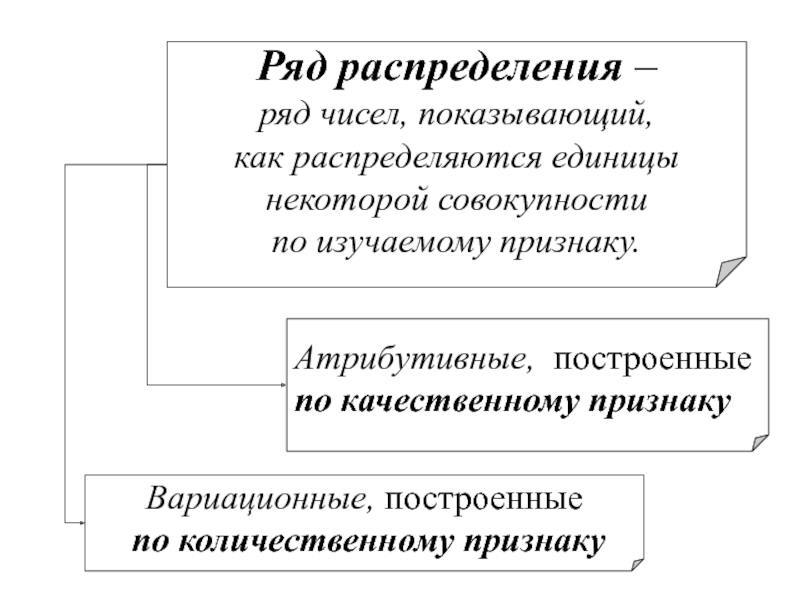
Слайд 21Ряд распределения –
ряд чисел, показывающий,
как распределяются единицы
некоторой
совокупности
по изучаемому признаку.
Атрибутивные, построенные
по качественному признаку
Вариационные, построенные
по количественному признаку
Слайд 22Вариационные ряды распределения
дискретные – основаны на прерывной вариации признака
интервальные
- непрерывные
Варианта – отдельное значение варьируемого признака, который он принимает
в ряду распределения
Частоты - это численности отдельных вариантов или каждой группы вариационного ряда. Частоты, выражающиеся в долях единицы, или в % к итогу, называются частостями.
Сумма всех частот называется объемом совокупности
Слайд 23Данные о стоимости основных фондов 50 предприятий:
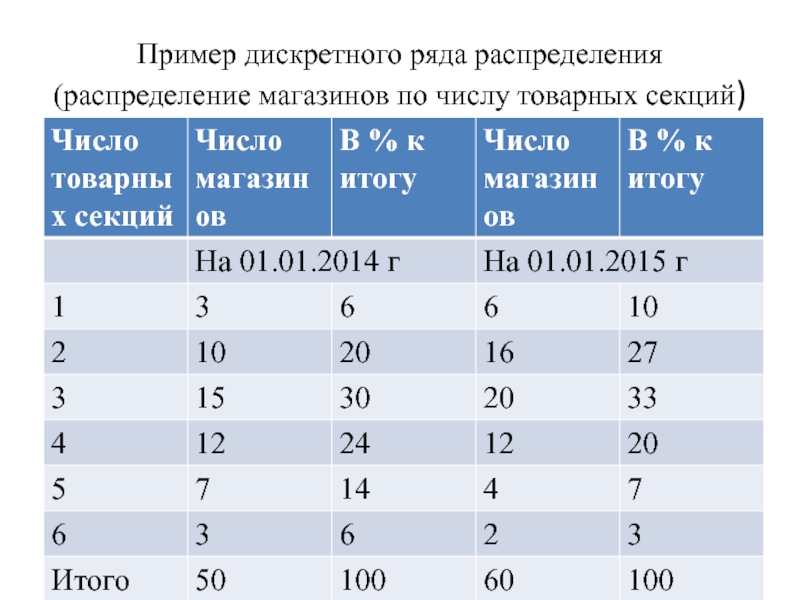
Слайд 24Пример дискретного ряда распределения (распределение магазинов по числу товарных секций)
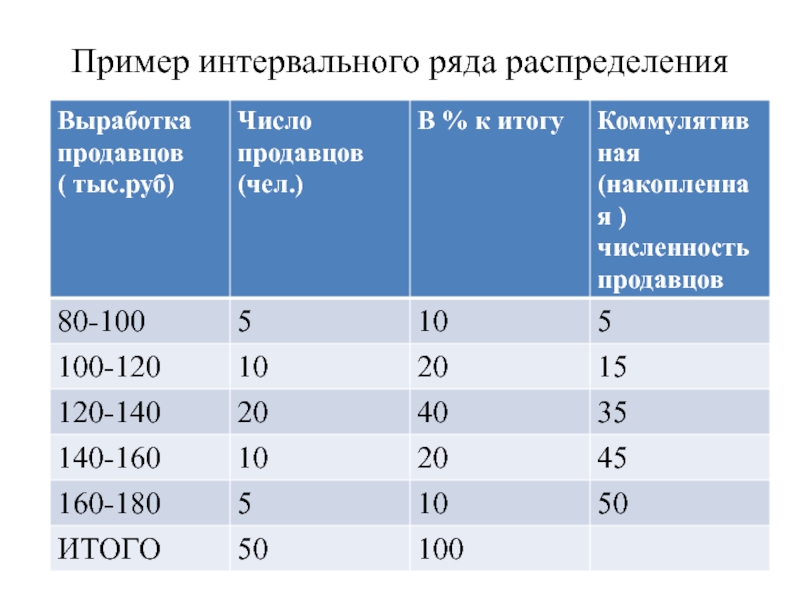
Слайд 25Пример интервального ряда распределения
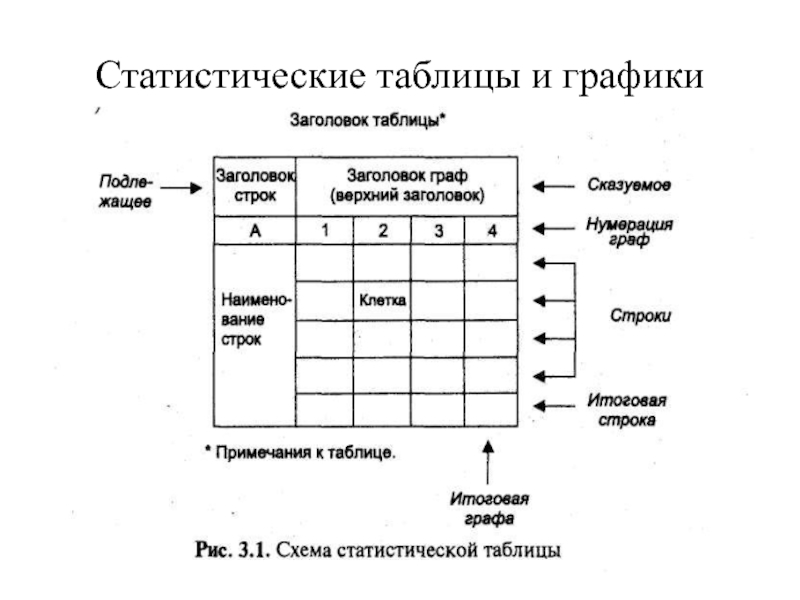
Слайд 26Статистические таблицы и графики
Слайд 27Составные части таблицы
Подлежащее таблицы (обычно помещается слева и составляет содержание
строк) показывает объект изучения, характеризующийся рядом показателей (сказуемым).
Сказуемое таблицы (записывается
сверху и составляет содержание граф) показывает, какими признаками (показателями) характеризуется объект (подлежащее).
Слайд 28Статистические графики
По содержанию или назначению : графики сравнения в
пространстве, графики различных относительных величин, графики вариационных рядов, графики размещения
по территории, графики взаимосвязанных показателей.
По способу построения делятся на диаграммы, картодиаграммы и картограммы.
По характеру графического образа различают графики точечные, линейные, плоскостные (столбиковые, почасовые, квадратные, круговые, секторные, фигурные) и объемные.
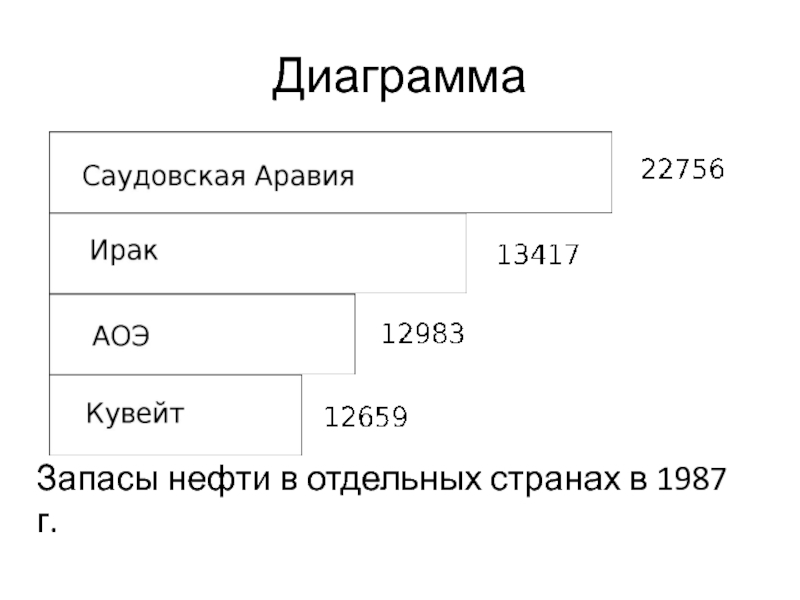
Слайд 29Диаграмма
Запасы нефти в отдельных странах в 1987 г.
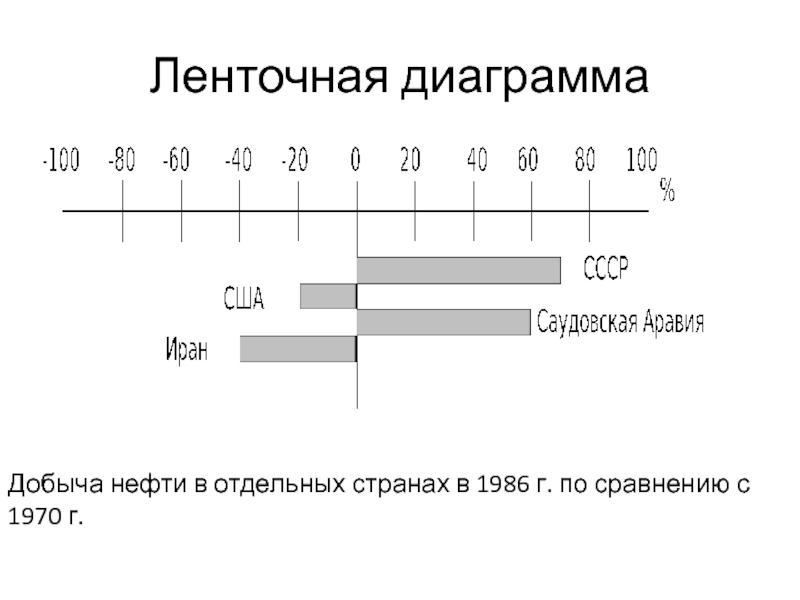
Слайд 30Ленточная диаграмма
Добыча нефти в отдельных странах в 1986 г. по
сравнению с 1970 г.
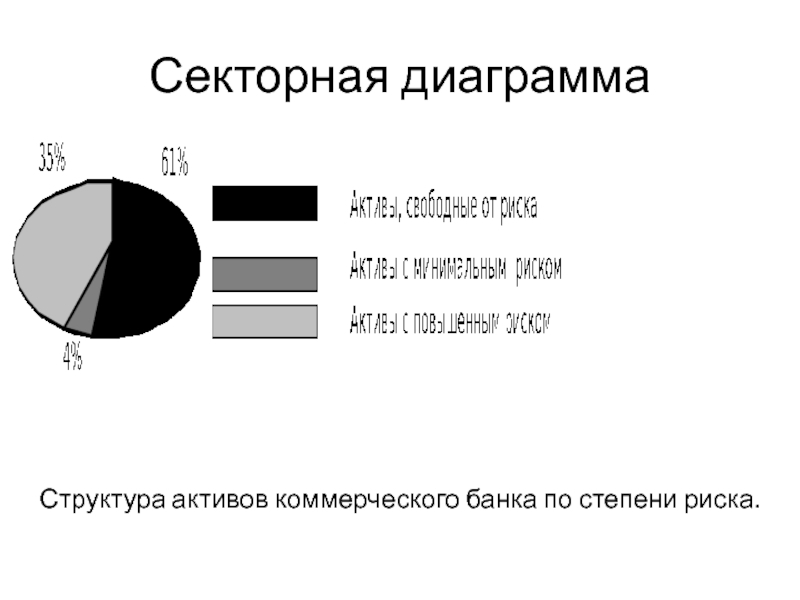
Слайд 31Секторная диаграмма
Структура активов коммерческого банка по степени риска.
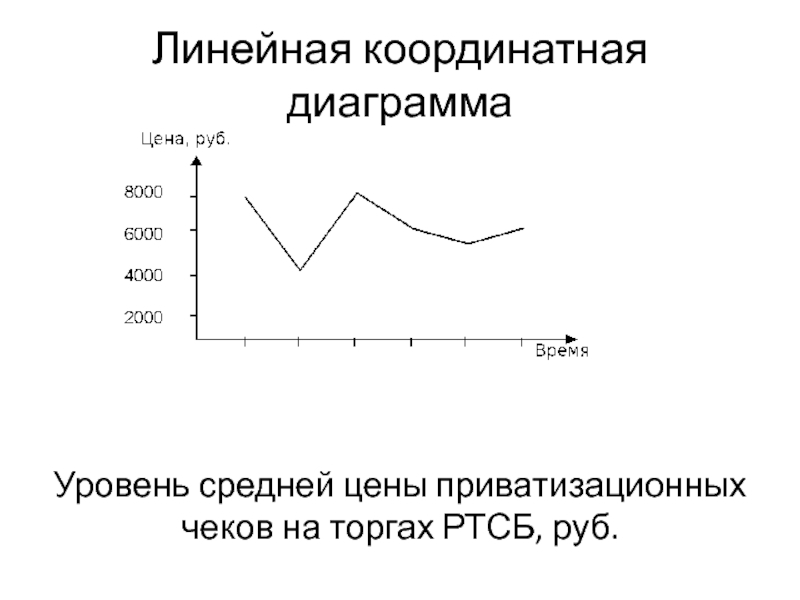
Слайд 32Линейная координатная диаграмма
Уровень средней цены приватизационных чеков на торгах РТСБ,
руб.
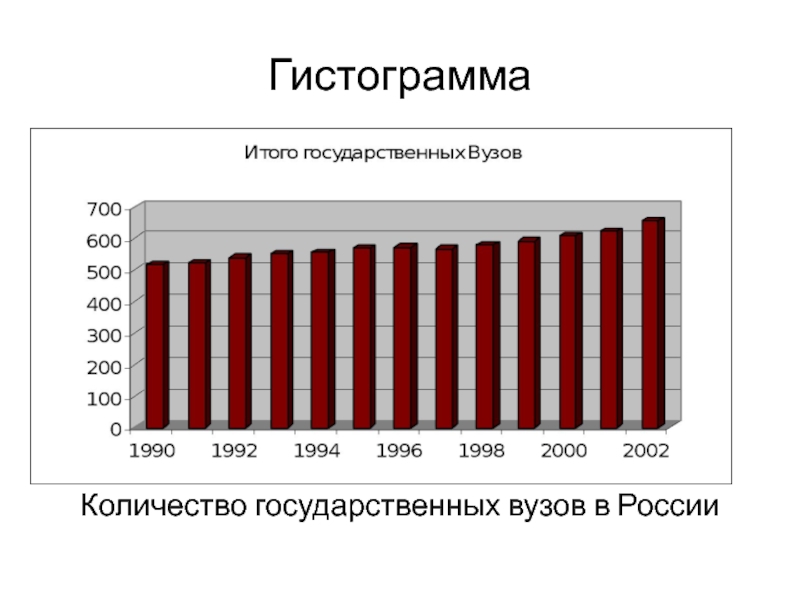
Слайд 34Гистограмма
Количество государственных вузов в России
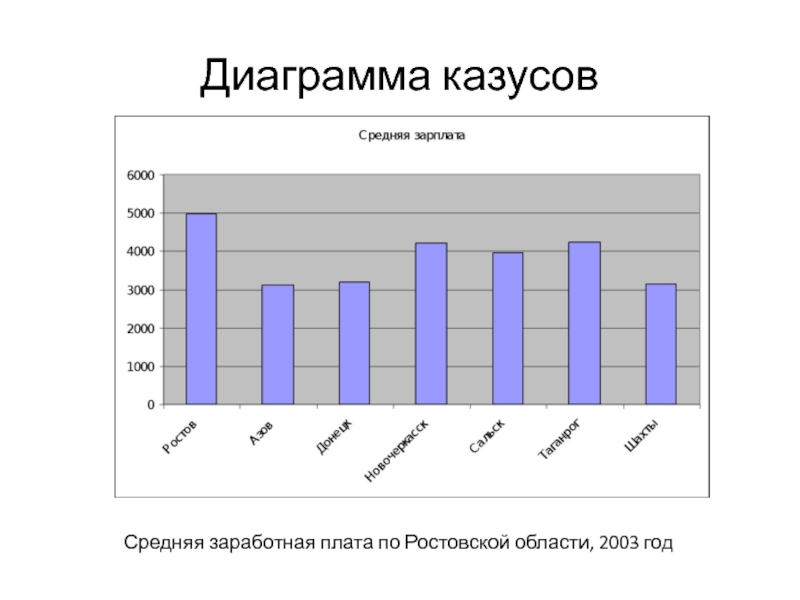
Слайд 35Диаграмма казусов
Средняя заработная плата по Ростовской области, 2003 год
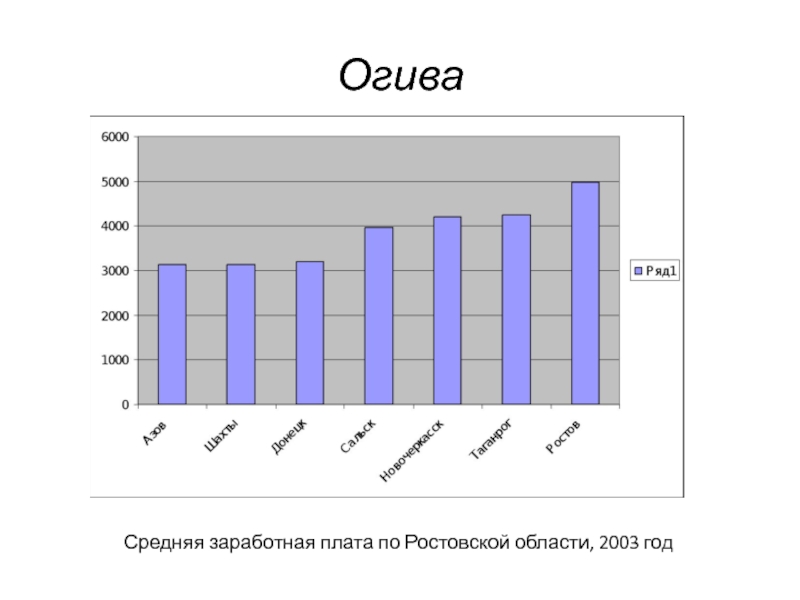
Слайд 36Огива
Средняя заработная плата по Ростовской области, 2003 год
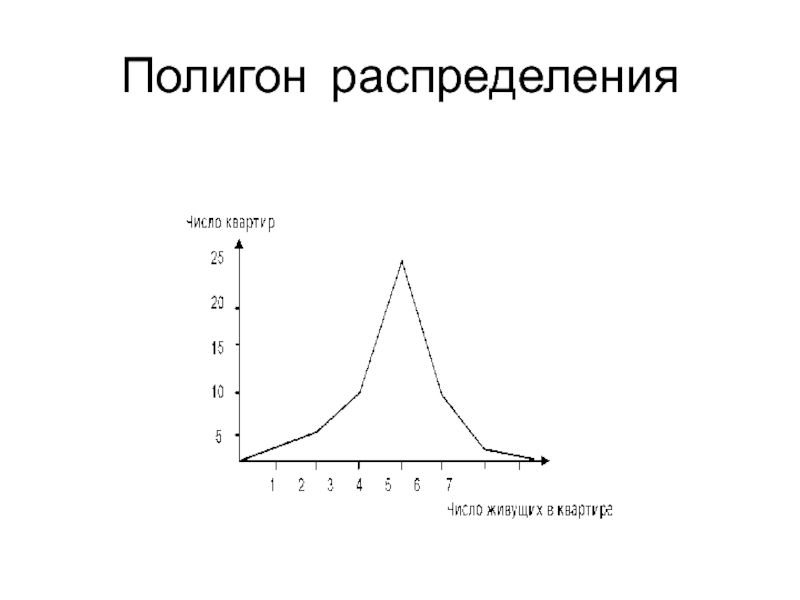
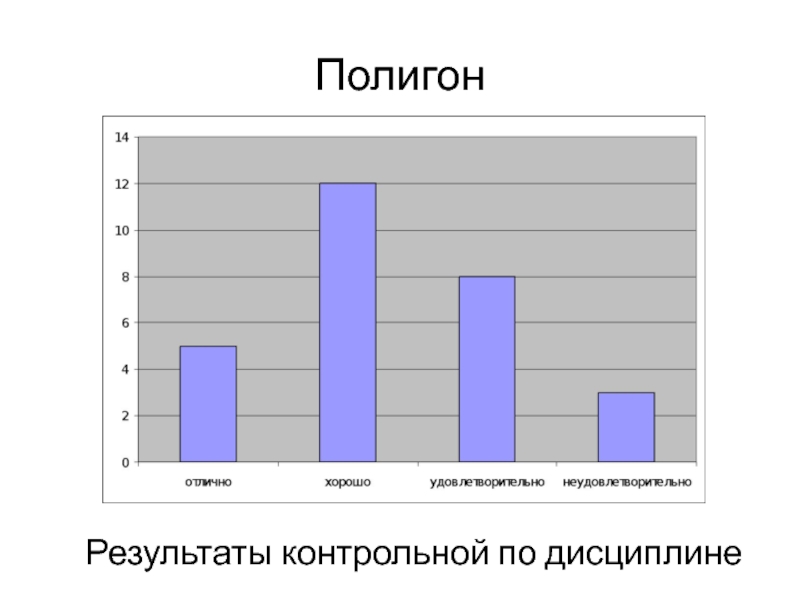
Слайд 37Полигон
Результаты контрольной по дисциплине
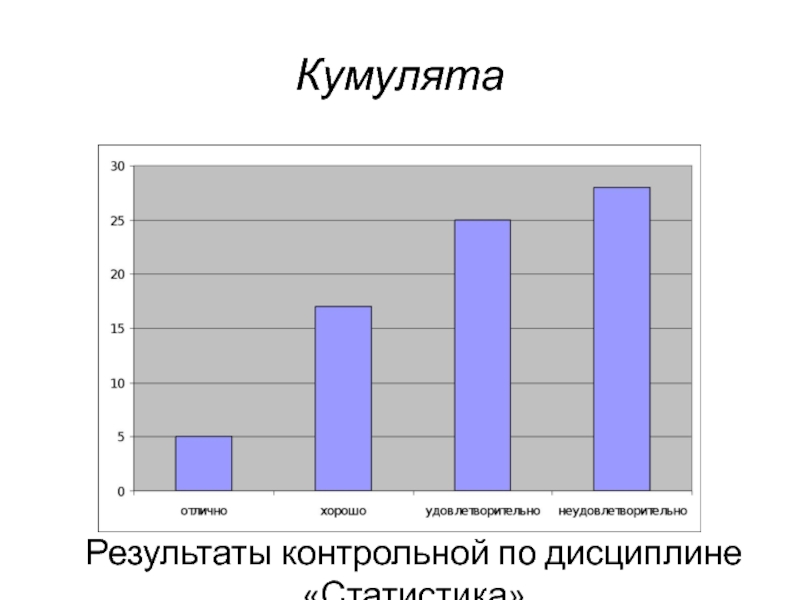
Слайд 38Кумулята
Результаты контрольной по дисциплине «Статистика»