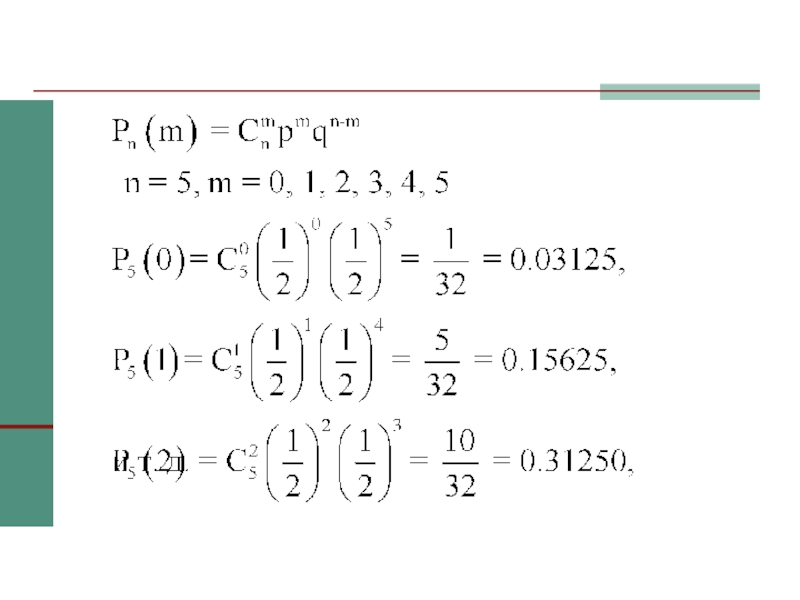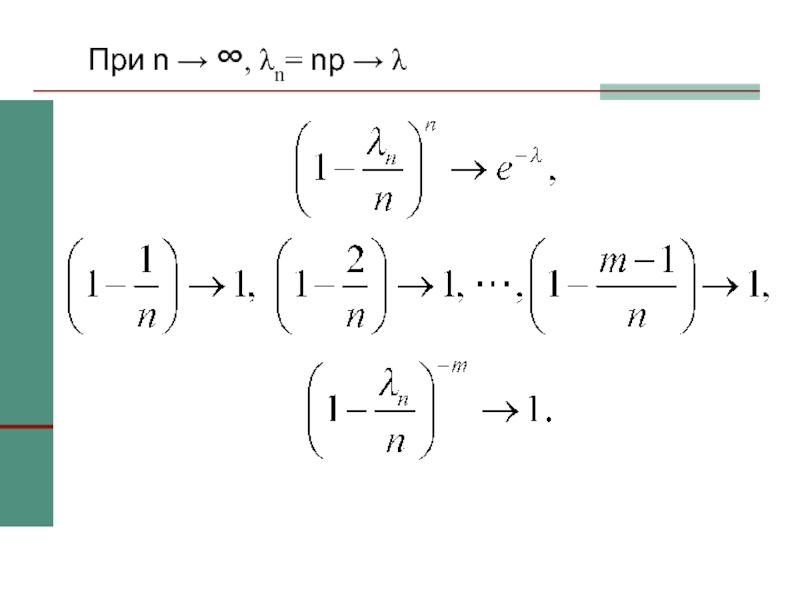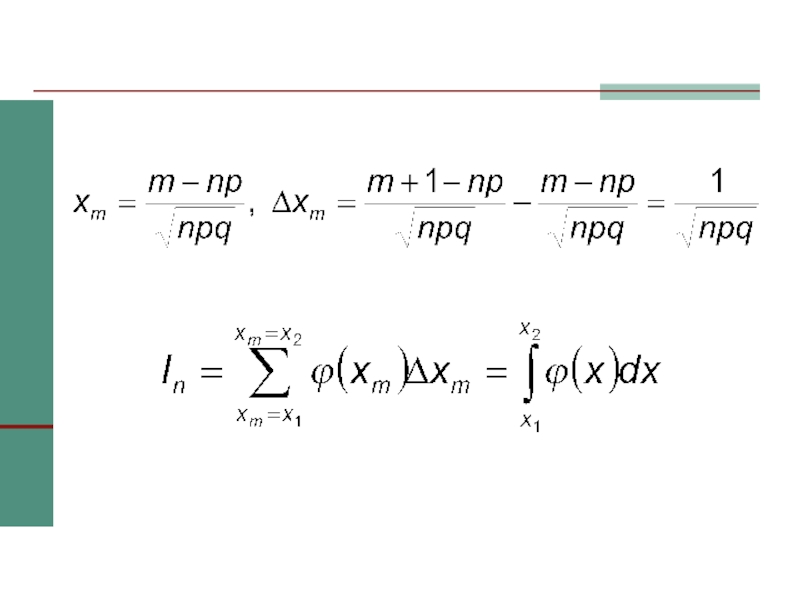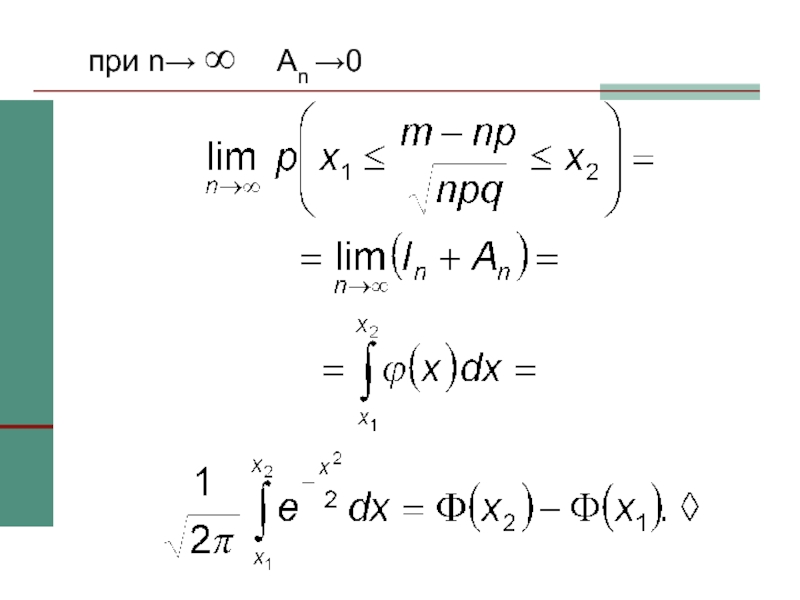Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Схемы бернули. Предельные теоремы
Содержание
- 1. Схемы бернули. Предельные теоремы
- 2. Схема Бернулли Определение Схемой Бернулли называется последовательность
- 3. Теорема (формула Бернулли) Обозначим через m число успехов
- 4. Поскольку испытания независимы, вероятность такого элементарного исхода
- 5. Поэтому событие A состоит из элементарных исходов, вероятность каждого из которых равна т.е.
- 6. Наивероятнейшее число успехов В испытаниях схемы Бернулли наиболее
- 7. Пример Вычислить вероятности всех возможных значений появления «герба»
- 8. Слайд 8
- 9. Наивероятнейшее число успехов:Вычисляем np + p =
- 10. Слайд 10
- 11. Еще один примерВероятность сдать экзамен равна 0,8.
- 12. Полиномиальная схемаОпределение Полиномиальной схемой называется последовательность n
- 13. Полиномиальная формула
- 14. ПримерЧеловек с вероятностью 0,2 оказывается брюнетом, с
- 15. Гипергеометрические испытания Пусть из совокупности n предметов, среди
- 16. Гипергеометрические вероятностиДанные испытания являются зависимыми.
- 17. Пример В урне 6 белых и 5
- 18. Теорема Пусть n → ∞ и n1→ ∞ так, что Тогда
- 19. Доказательство
- 20. Предельные теоремы для схемы Бернулли При числе испытаний,
- 21. Теорема Пуассона Если n → ∞, р
- 22. Доказательство Пусть np =λn. Тогда
- 23. При n → ∞, λn= np → λ
- 24. Следовательно,
- 25. Приближенная формула Пуассона где λ = np.
- 26. Пример (дни рождения) Какова вероятность, что среди 500
- 27. По приближенной формуле Пуассона
- 28. Предельная теорема Муавра –Лапласа Если при n→ ∞
- 29. Доказательство этой теоремы основано на применении формулы Стирлинга
- 30. Локальная приближенная формула Муавра –ЛапласаЛокальную приближенную формулу
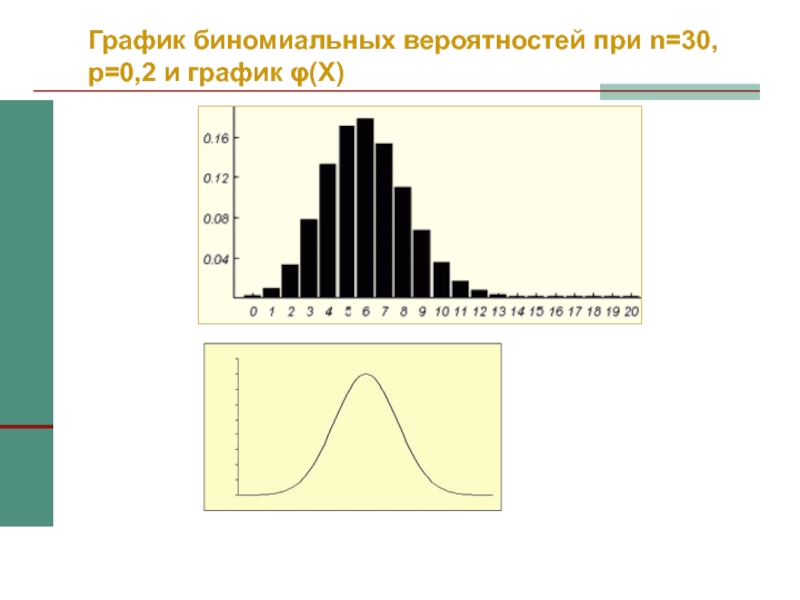
- 31. График биномиальных вероятностей при n=30, p=0,2 и график φ(X)
- 32. Интегральная предельная теорема Муавра –Лапласа При n→
- 33. Доказательство
- 34. По локальной предельной теореме
- 35. Слайд 35
- 36. Слайд 36
- 37. при n→ ∞ An →0
- 38. Интегральная приближенная формула Муавра –ЛапласаИнтегральную приближенную формулу
- 39. Следствия
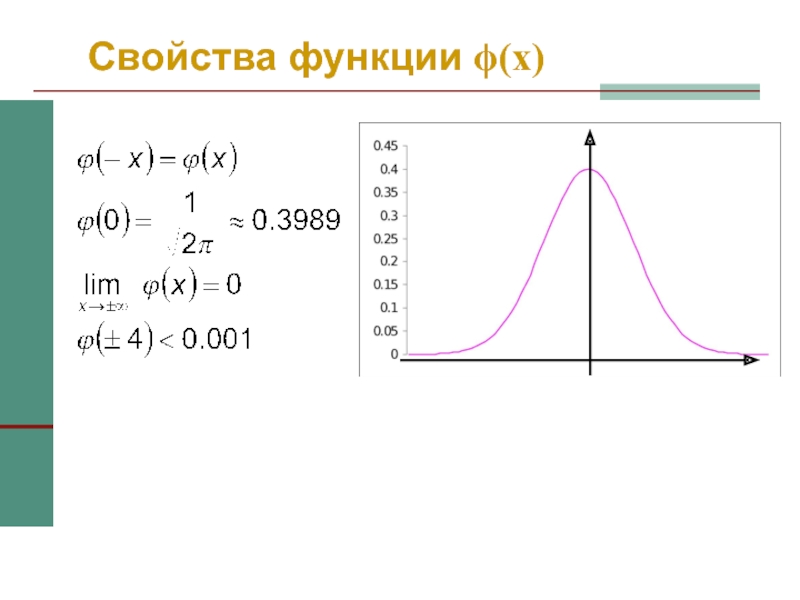
- 40. Свойства функции ϕ(x)
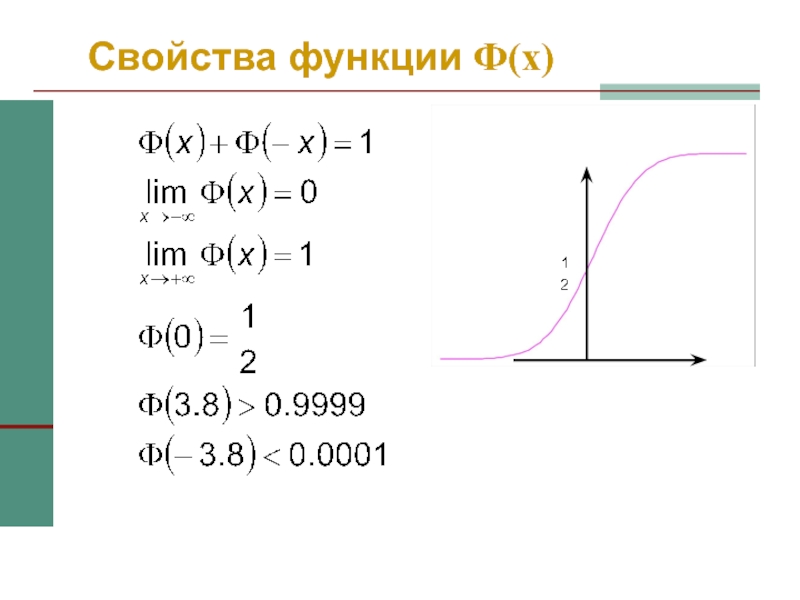
- 41. Свойства функции Ф(x)
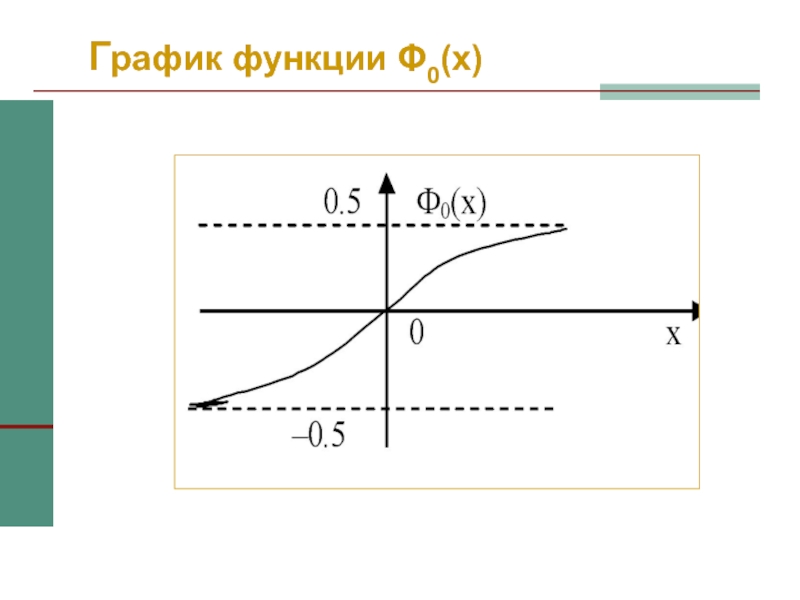
- 42. Функция Лапласа Φ0(x). Вместо Φ(x) часто используют функцию Лапласа Φ0(x).
- 43. График функции Φ0(x)
- 44. Замечанияпоэтому в формулах может использоваться как Φ(x), так и Φ0(x).Значения функций находят в таблицах.
- 45. ПримерВероятность рождения мальчика p = 0,5. Найти
- 46. Скачать презентанцию
Схема Бернулли Определение Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода — «успех» и «неудача», при этом «успех» в одном испытании происходит с вероятностью p,
Слайды и текст этой презентации
Слайд 2Схема Бернулли
Определение
Схемой Бернулли называется последовательность независимых испытаний, в
Слайд 3Теорема (формула Бернулли)
Обозначим через m число успехов в n испытаниях
схемы Бернулли. Тогда
Доказательство
Событие A = {число успехов равно m}
означает, что в n испытаниях схемы Бернулли произошло ровно m успехов. Рассмотрим один из благоприятных исходов:
Слайд 4
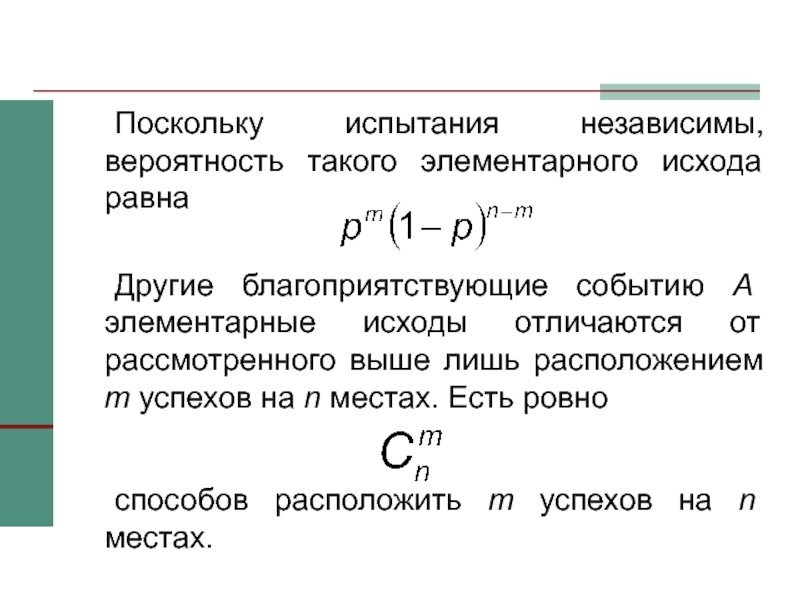
Поскольку испытания независимы, вероятность такого элементарного исхода равна
Другие благоприятствующие событию
A элементарные исходы отличаются от рассмотренного выше лишь расположением m
успехов на n местах. Есть ровноспособов расположить m успехов на n местах.
Слайд 5
Поэтому событие A состоит из
элементарных исходов, вероятность каждого
из которых равна
т.е.
Слайд 6Наивероятнейшее число успехов
В испытаниях схемы Бернулли наиболее вероятным числом успехов
является
a) единственное число m0 = [np + p] (целая
часть), если число np + p не целое; б) два числа
m0 = np + p и m0' = np + p – 1, если число np + p целое.
Слайд 7Пример
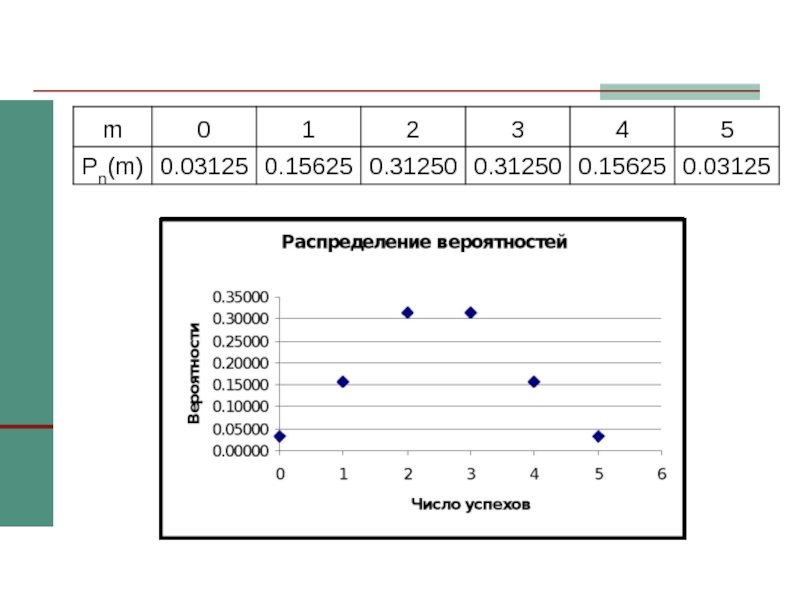
Вычислить вероятности всех возможных значений появления «герба» при 5 бросаниях
монеты. Построить график распределения этих вероятностей.
Решение
Число независимых испытаний n =
5.Число успехов m = 0, 1, 2, 3, 4, 5.
Вероятность успеха в одном испытании p = 0,5.
Слайд 9
Наивероятнейшее число успехов:
Вычисляем np + p = 5∙1/2 + ½
= 3.
Это целое число, поэтому
m0 = np + p
= 3 и m0' = np + p – 1 = 2.Самые большие (и равные между собой) вероятности у двух и трех появлений герба.
Слайд 11Еще один пример
Вероятность сдать экзамен равна 0,8. Найти наивероятнейшее число
студентов, сдавших экзамен в группе из 30 человек.
Решение.
Вычисляем np
+ p = 30∙0,8 + 0,8 = 24,8.Это не целое число, поэтому
m0 = [24,8] = 24.
Слайд 12Полиномиальная схема
Определение
Полиномиальной схемой называется последовательность n независимых одинаковых испытаний,
в каждом из которых возможны k исходов
при этом вероятность
любого исхода в каждом испытании постоянна,
Слайд 14Пример
Человек с вероятностью 0,2 оказывается брюнетом, с вероятностью 0,4 —шатеном,
с вероятностью 0,3 — блондином и с вероятностью 0,1—рыжим. Выбирается
наугад группа из шести человек. Найти вероятность того, что в составе группы два брюнета, один шатен и три блондина.
Слайд 15Гипергеометрические испытания
Пусть из совокупности n предметов, среди которых n1 предметов
первого вида и n2 предметов второго вида (n1 + n2
= n) производится выборка без возвращения m предметов, 1 ≤ m ≤ n.Вероятность того, что в выборке будет m1 предметов первого вида и m2 предметов второго вида (m1 + m2 = m), согласно классическому определению вероятности, выражается формулой
Слайд 17Пример
В урне 6 белых и 5 черных шаров.
Из урны вынимают наугад 5 шаров. Найти вероятность, что два из них будут белыми, а три – черными.
Решение:
Слайд 20Предельные теоремы для схемы Бернулли
При числе испытаний, превышающем 20, вычисление
точного значения Pn(m) затруднительно. В этих случаях применяют приближенные формулы,
вытекающие из предельных теорем.Различают два случая:
когда р мало, используют приближение Пуассона,
когда р не мало (и не очень близко к единице), справедливо приближение Муавра –Лапласа.
Существует область, в которой возможно применение обоих приближений.
Слайд 21Теорема Пуассона
Если n → ∞, р → 0 так,
что np → λ, 0 < λ < ∞, то
для любого фиксированного m∈N справедливо:
Слайд 25Приближенная формула Пуассона
где λ = np. Приближенную формулу Пуассона
применяют при
n > 30,
р < 0.1,
0.1
λ = np < 10. 
Слайд 26Пример (дни рождения)
Какова вероятность, что среди 500 случайно выбранных людей
ни один не родился 1 января ?
Решение
По формуле Бернулли
Слайд 28Предельная теорема Муавра –Лапласа
Если при n→ ∞ и постоянном р,
не равном 0 или 1, величина
ограничена так, что –
∞ < а ≤ хт ≤ b < + ∞, то 
Слайд 30Локальная приближенная формула Муавра –Лапласа
Локальную приближенную формулу Муавра –
Лапласа применяют
при
n > 30, 0.1 ≤ p ≤ 0.9,
nрq > 9. 
Слайд 38Интегральная приближенная формула Муавра –Лапласа
Интегральную приближенную формулу Муавра –
Лапласа применяют
при n > 30, 0.1 ≤ p ≤ 0.9, nрq >
9.
Слайд 44Замечания
поэтому в формулах может использоваться как Φ(x), так и Φ0(x).
Значения
функций находят в таблицах.
Слайд 45Пример
Вероятность рождения мальчика p = 0,5. Найти вероятность того, что
в группе из 100 новорожденных мальчиков не меньше 60.
Решение.
