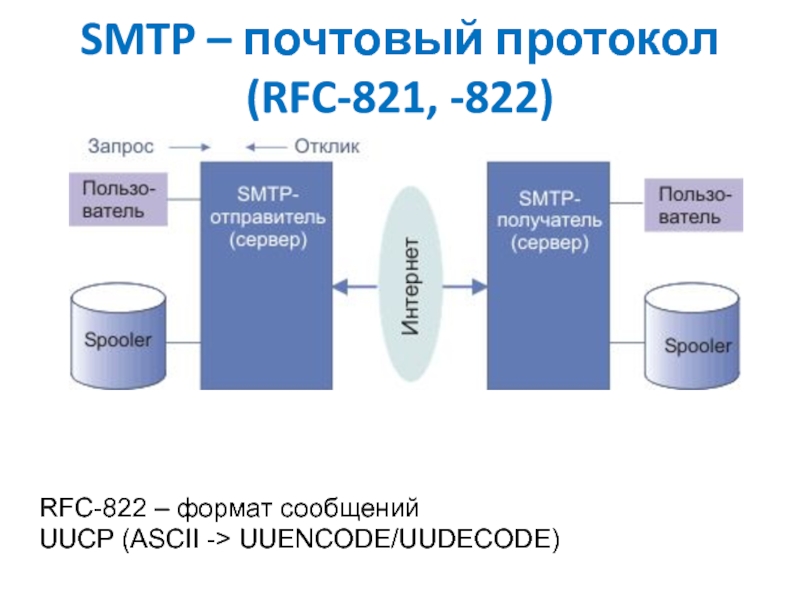
найти такое значение
при котором функция
принимает экстремальное значение (минимальное
или максимальное). Процесс поиска экстремального значения иногда называют оптимизацией.
называют оптимизируемой или целевой функцией
называют вектором параметров оптимизации
В области определения функции может быть несколько экстремумов.
Все существующие методы многомерной оптимизации позволяют определить лишь один из экстремумов. Какой именно экстремум будет определён, зависит от выбора
начального приближения:
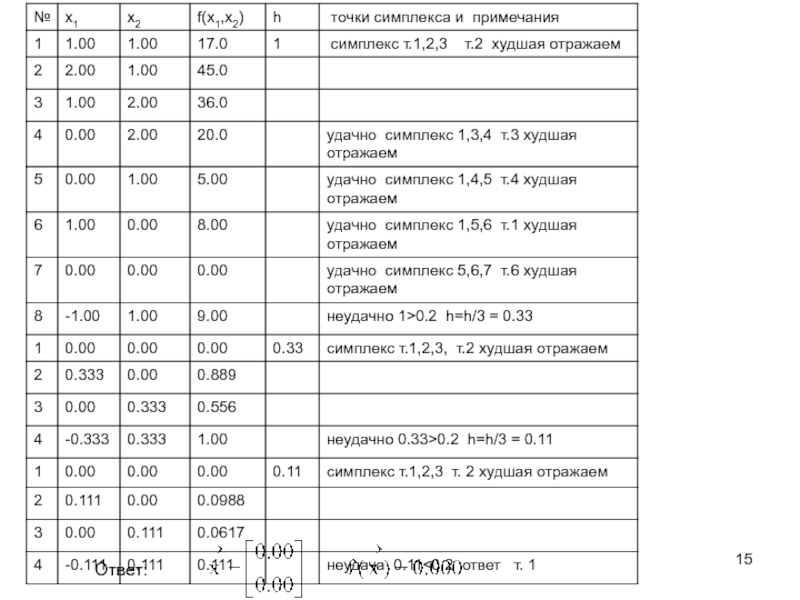
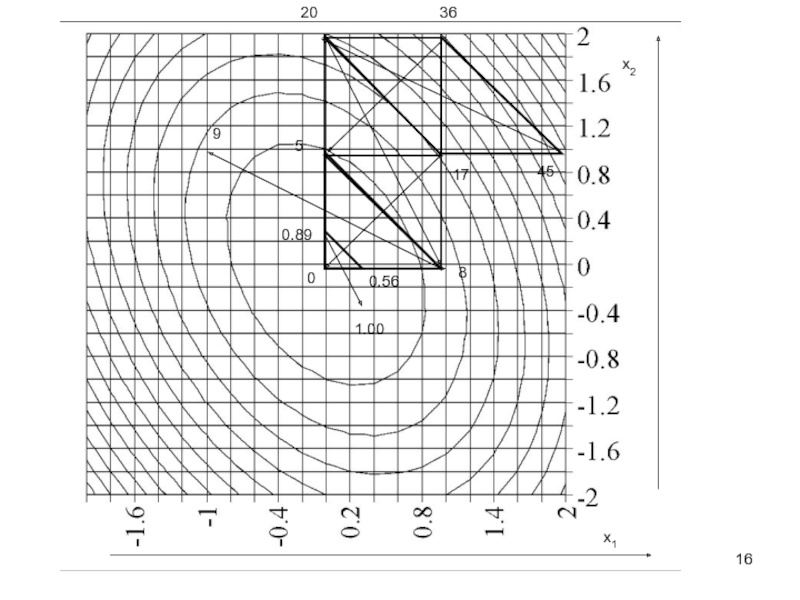
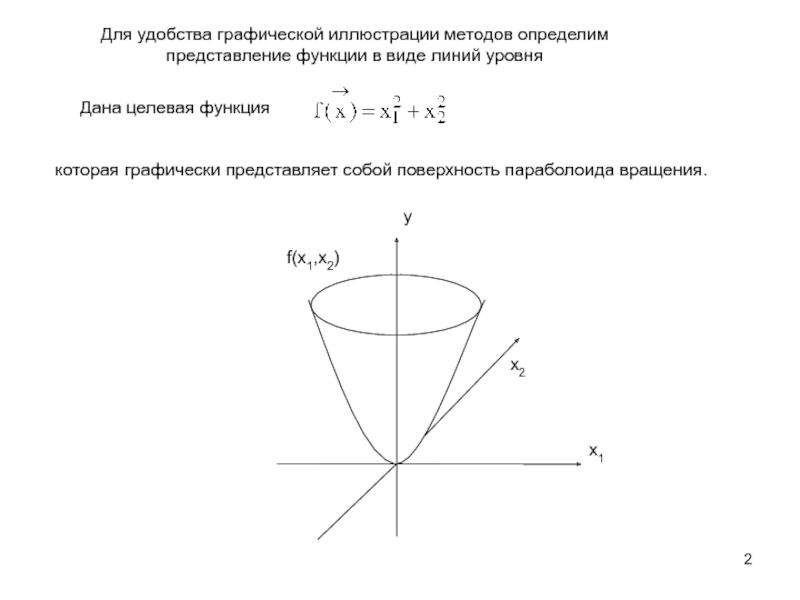
Методы поиска экстремума будем рассматривать относительно случая поиска минимума, для функции двух переменных


![VM-11-m-Многомерн-Оптимизация.ppt функция Химмельблауfxx01=inline('(x1.^2+x2-11).^2+(x1+x2.^2-7).^2')[x1,x2]=meshgrid(-4:0.05:4);z=fxx01(x1,x2);contour(x1,x2,z) функция Химмельблауfxx01=inline('(x1.^2+x2-11).^2+(x1+x2.^2-7).^2')[x1,x2]=meshgrid(-4:0.05:4);z=fxx01(x1,x2);contour(x1,x2,z)](/img/thumbs/2160a662a42c7a73d7e560f821657969-800x.jpg)

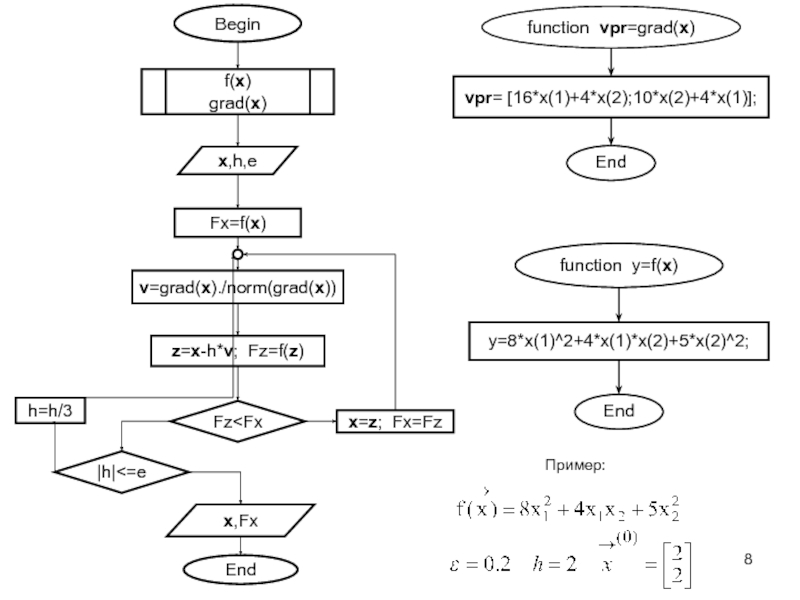
![VM-11-m-Многомерн-Оптимизация.ppt function[xm,Fm]=rvs(x,v,h,e)x=xm-h*vFx:=f(x)Fx function[xm,Fm]=rvs(x,v,h,e)x=xm-h*vFx:=f(x)Fx](/img/thumbs/7c6894808c4f24f82c45773606f36624-800x.jpg)
![VM-11-m-Многомерн-Оптимизация.ppt function y=f(x);y=8*x(1)^2+4*x(1)*x(2)+5*x(2)^2;function g=grad(x);g=[16 * x(1) + 4 * x(2); 10 * function y=f(x);y=8*x(1)^2+4*x(1)*x(2)+5*x(2)^2;function g=grad(x);g=[16 * x(1) + 4 * x(2); 10 * x(2) + 4 * x(1)];Симплексный](/img/thumbs/3eb965b9620112568b3ddb5c2eb4faf8-800x.jpg)