Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сжатие данных
Содержание
- 1. Сжатие данных
- 2. Сжатие данных— алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого ими объёма
- 3. Коэффициент сжатия – соотношение исходного и сжатого файла
- 4. Слайд 4
- 5. Алгоритмы сжатия
- 6. Алгоритм RLE -кодирование цепочек одинаковых символов100100200 байтовФайл qq.txtФайл qq.rle (сжатый)4 байта+-
- 7. Префиксный код – это код, в котором
- 8. Код Шеннона-ФаноСообщения алфавита источника выписывают в порядке
- 9. Код Шеннона-ФаноКоличество символов в сообщении: На 2
- 10. Код Шеннона-Фаноучитывается частота символовне нужен символ-разделителькод префиксный
- 11. Алгоритм ХаффманаБуквы алфавита сообщений выписывают в основной
- 12. Алгоритм Хаффмана10_ - 1О – 01Е – 001Н – 0001Т – 0000 _ОЕНТ101010
- 13. Алгоритм Хаффманакод оптимальный среди алфавитных кодовнужно заранее
- 14. Слайд 14
- 15. Сжатие с потерями
- 16. Алгоритм JPEGПри сжатии изображение преобразуется из цветового
- 17. Сжатие JPEGИдея: глаз наиболее чувствителен к яркости12 чиселДано: изображение 2×2 pt
- 18. Сжатие звука (MP3)Битрейт – это число бит,
- 19. Сжатие: итогиХорошо сжимаются:тексты (*.txt)документы (*.doc)несжатые рисунки (*.bmp)несжатый
- 20. 5. Производилась двухканальная (стерео) звукозапись с частотой
- 21. 6. Музыкальный фрагмент был оцифрован и записан
- 22. 7. Рисунок размером 512 на 256 пикселей
- 23. 8. Какой минимальный объём памяти (в Кбайт)
- 24. Скачать презентанцию
Сжатие данных— алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого ими объёма
Слайды и текст этой презентации
Слайд 2Сжатие данных— алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого
ими объёма
Слайд 6Алгоритм RLE -кодирование цепочек одинаковых символов
100
100
200 байтов
Файл qq.txt
Файл qq.rle (сжатый)
4
байта
+
-
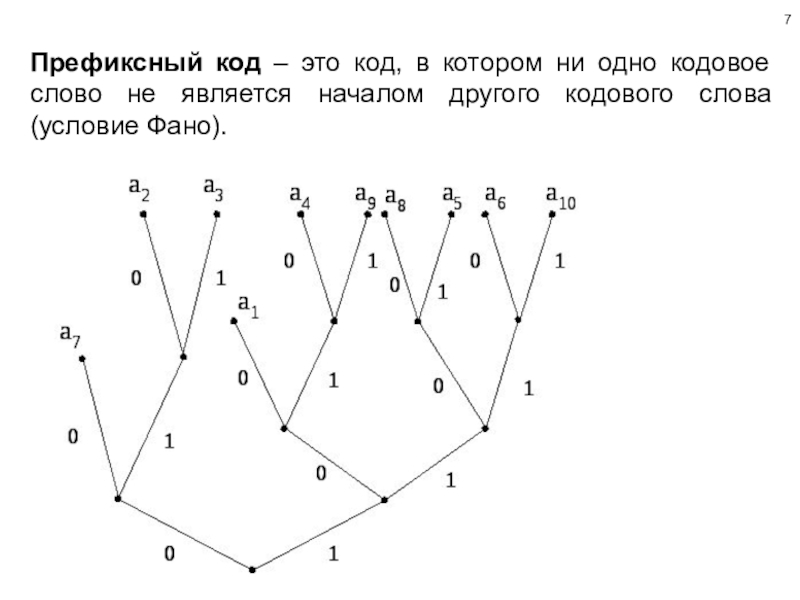
Слайд 7Префиксный код – это код, в котором ни одно кодовое
слово не является началом другого кодового слова (условие Фано).
Слайд 8Код Шеннона-Фано
Сообщения алфавита источника выписывают в порядке убывания вероятностей их
появления.
Далее разделяют их на две части так, чтобы суммарные
вероятности сообщений в каждой из этих частей были по возможности почти одинаковыми. Припишем сообщениям первой части в качестве первого символа – 0, а второй – 1 (можно наоборот).
Затем каждая из этих частей (если она содержит более одного сообщения) делится на две по возможности равновероятные части, и в качестве второго символа для первой из них берется 0, а для второй – 1.
Этот процесс повторяется, пока в каждой из полученных частей не останется по одному сообщению
Слайд 9Код Шеннона-Фано
Количество символов в сообщении:
На 2 группы с примерно
равным числом символов:
начинаются с 0
начинаются с 1
начинаются с 11
+
-
Слайд 10Код Шеннона-Фано
учитывается частота символов
не нужен символ-разделитель
код префиксный – можно декодировать
по мере поступления данных
нужно заранее знать частоты символов
код неоптимален
при ошибке
в передаче сложно восстановить «хвост»не учитывает повторяющиеся последовательности символов
Слайд 11Алгоритм Хаффмана
Буквы алфавита сообщений выписывают в основной столбец таблицы кодирования
в порядке убывания вероятностей.
Две последние буквы объединяют в одну
вспомогательную букву, которой приписывают суммарную вероятность. Вероятность букв, не участвовавших в объединении, и полученная суммарная вероятность слова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяют.
Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице
Слайд 13Алгоритм Хаффмана
код оптимальный среди алфавитных кодов
нужно заранее знать частоты символов
при
ошибке в передаче сложно восстановить «хвост»
не учитывает повторяющиеся последовательности символов
Слайд 16Алгоритм JPEG
При сжатии изображение преобразуется из цветового пространства RGB в
YCbCr (Y – яркость, Cb – «синева», Cr- «краснота»
Перевод осуществляется
по следующей формуле
Слайд 18Сжатие звука (MP3)
Битрейт – это число бит, используемых для кодирования
1 секунды звука (Кб/с)
Дано:
d=44 кГц
S=2
t=1 c
b=16 б
Битрейт =256 Кб/с
Степень
сжатия - ?V = bd t S
V=44000 16 1 2= 1375
Степень сжатия=1375/256=5
Слайд 19Сжатие: итоги
Хорошо сжимаются:
тексты (*.txt)
документы (*.doc)
несжатые рисунки (*.bmp)
несжатый звук (*.wav)
несжатое видео
(*.avi)
Плохо сжимаются:
случайные данные
сжатые данные в архивах (*.zip, *.rar, *.7z)
сжатые рисунки
(*.jpg, *.gif, *.png)сжатый звук (*.mp3, *.aac)
сжатое видео (*.mpg, *.mp4, *.mov)
Слайд 205. Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц
и 24-битным разрешением. В результате был получен файл размером 120
Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) производилась запись. В качестве ответа укажите ближайшее к времени записи целое число, кратное 5.
Слайд 216. Музыкальный фрагмент был оцифрован и записан в виде файла
без использования сжатия данных. Получившийся файл был передан в город
А по каналу связи за 30 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.
Слайд 227. Рисунок размером 512 на 256 пикселей занимает в памяти
64 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов
в палитре изображения.
Слайд 238. Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы
можно было сохранить любое растровое изображение размером 64 на 64
пикселов при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
