Тайны корреляционных связей в статистике (Анализ корреляций)

корреляции. Вычисление линейного коэффициента корреляции Пирсона. Условия применимости
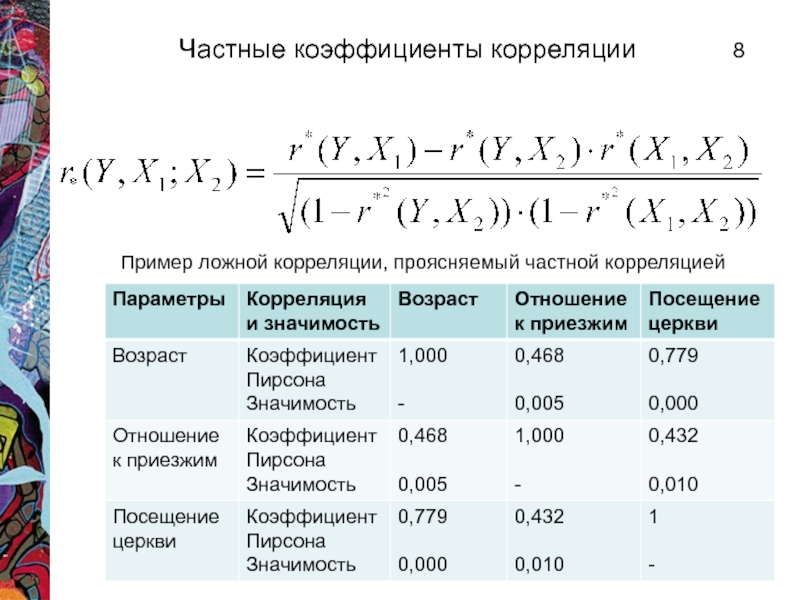
Частная корреляция. Величина

и надежность зависимости
Функции распределения. Нормальное распределение
Ложные корреляции
Некоррелированность и независимость
Ранговые коэффициенты корреляции
Если распределения ненормальны
Закон больших чисел и коэффициент корреляции
Закон Гаусса в мире случайного
Доверительные границы

связей в статистике. – М.: Научная книга: ИНФРА-М, 2009

(двумерные методы исследования)

Понятие зависимости (связи двух переменных) не тождественно понятию причинности (каузальной связи);
Связь между переменными означает согласованное изменение двух переменных;
Зависимость (связь) носит вероятностный характер;
Методы и алгоритмы определения взаимосвязи переменных зависят от типов переменных.
Переменные любых типов связаны (зависимы) между собой, если наблюдаемые значения этих переменных изменяются (распределены) согласованным образом (если зная значение одной переменной, мы можем предсказать значение другой).
Наиболее распространенное понятие для обозначения связи двух переменных – корреляция.
(Ф. Гальтон (1822-1911), К. Пирсон (1857-1936) – основоположники корреляционного анализа))

(двумерные методы исследования)

Коэффициент корреляции предполагает:
две переменные измеряются по крайней мере в интервальной шкале;

определяет степень, с какой значения двух переменных пропорциональны друг другу;

является безразмерной величиной, изменяется от -1 до +1;

корреляция может быть положительной и отрицательной;

рассчитывается по формуле:

Коэффициент определен только для линейных зависимостей. Это значит,

что возможно его искажение по следующим причинам:
1. Наличие выбросов, т. е. нетипичных, резко выделяющихся наблюдений;
2. Отсутствие однородности в имеющихся данных. В таком случае необходимо вычислять корреляцию для каждой отдельной группы данных.
3. Наличие нелинейной зависимости между переменными.
Во всех случаях нужна визуализация данных для проверки всех вышеперечисленных условий (диаграмма рассеяния).

Пример ложной корреляции, проясняемый

частной корреляцией

Величина и надежность зависимости

Корреляция характеризуется:
Величиной зависимости;
Надежностью ( истинностью) зависимости (насколько можно распространить полученную на выборке величину зависимости на генеральную совокупность).

Надежность показывает, насколько вероятно, что зависимость будет вновь обнаружена (подтвердится) на данных другой выборки, извлеченной из той же популяции.

Если исследование удовлетворяет некоторым специальным критериям, то надежность найденных зависимостей между переменными выборки можно количественно оценить и представить с помощью стандартной статистической меры, р-уровень, или статистический уровень значимости.

Если исследование удовлетворяет некоторым специальным критериям,

то надежность найденных зависимостей между переменными выборки можно количественно оценить и представить с помощью стандартной статистической меры, р-уровень, или статистический уровень значимости.
Р- уровень – это показатель, находящийся в убывающей зависимости от надежности результата. Р-уровень представляет вероятность ошибки, связанной с распространением наблюдаемого результата на всю генеральную совокупность.