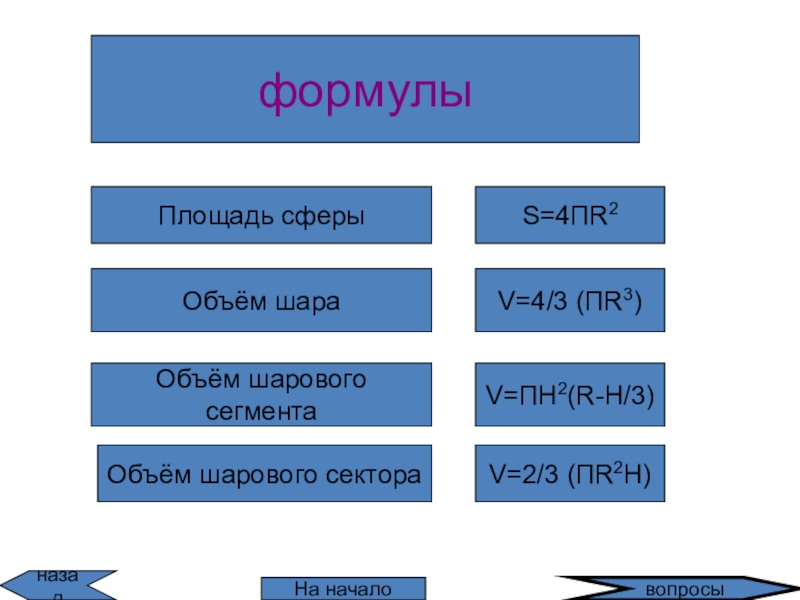
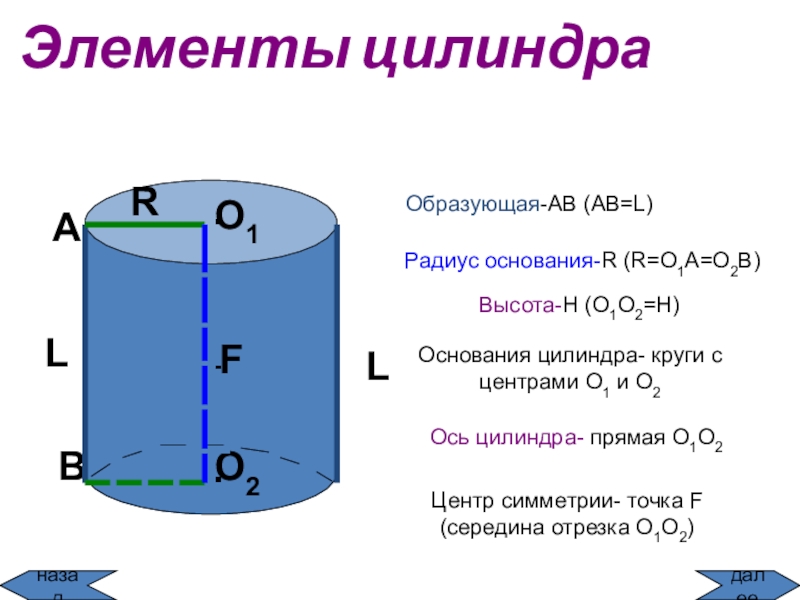
всех отрезков,
соединяющих соответствующие точки этих кругов.
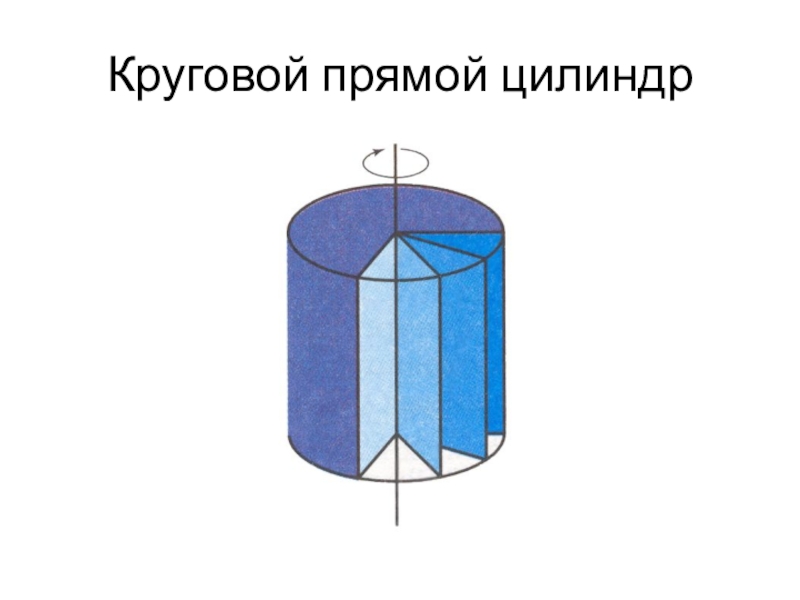
Вращением прямоугольника
вокруг одной из сторон прямоугольника или вокруг оси симметрии прямоугольника.
далее
На начало
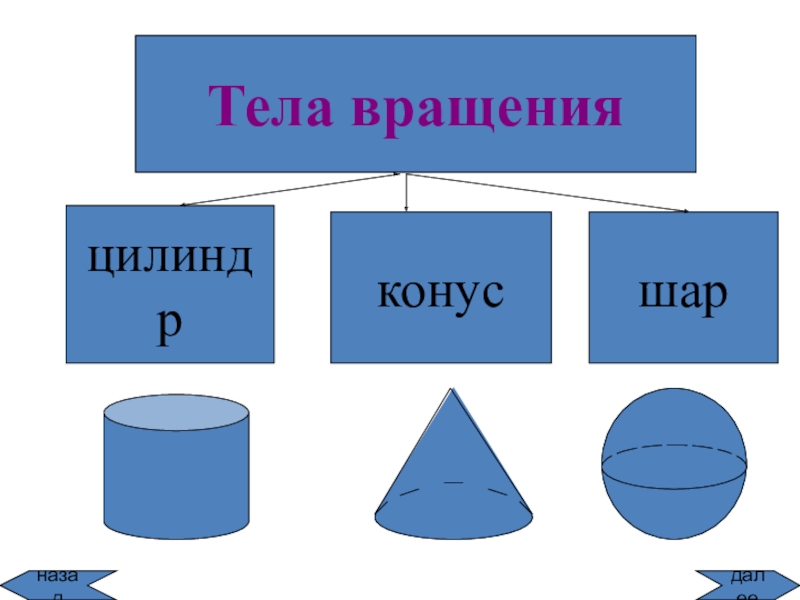



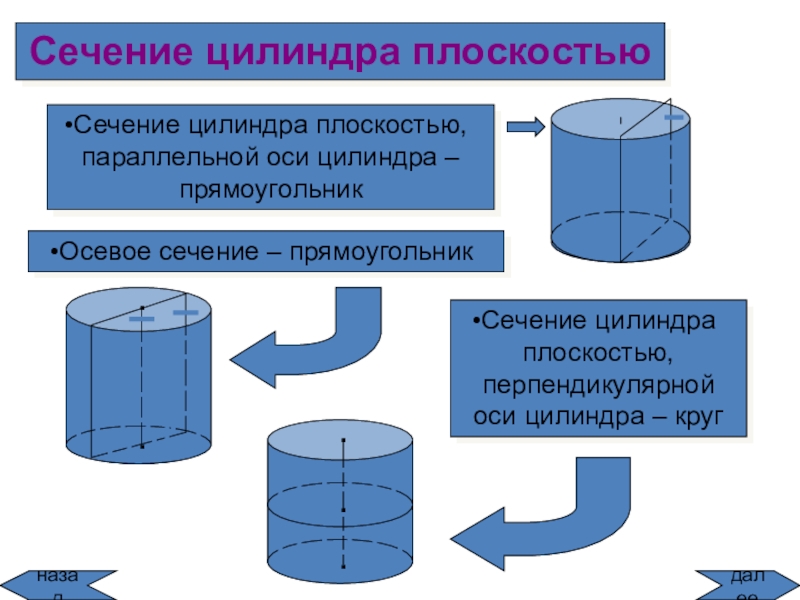
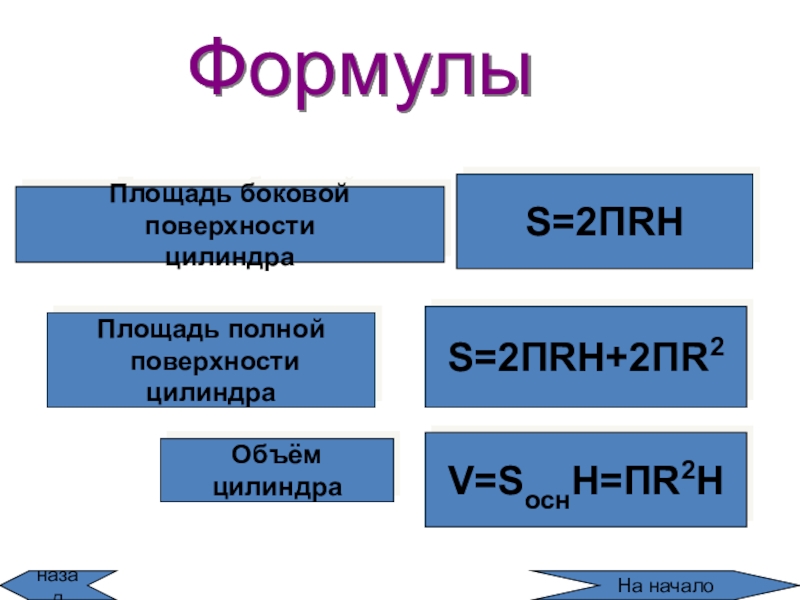

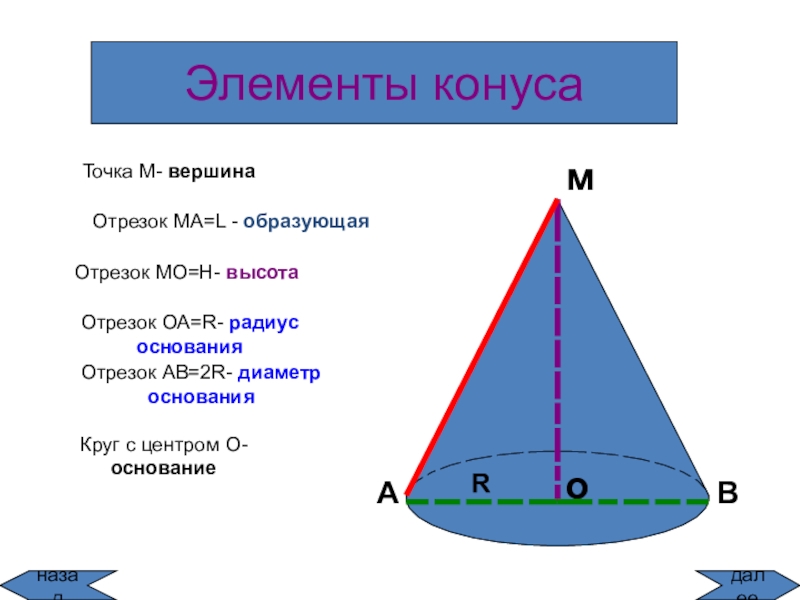

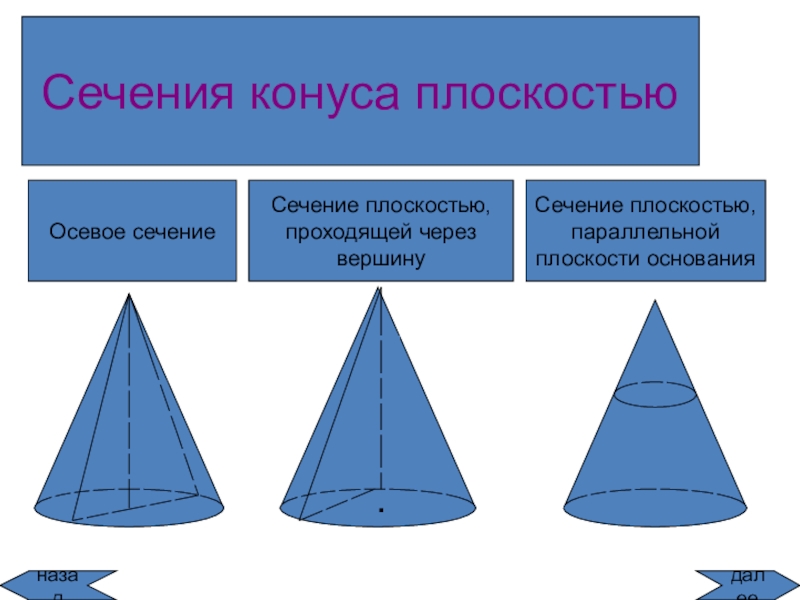

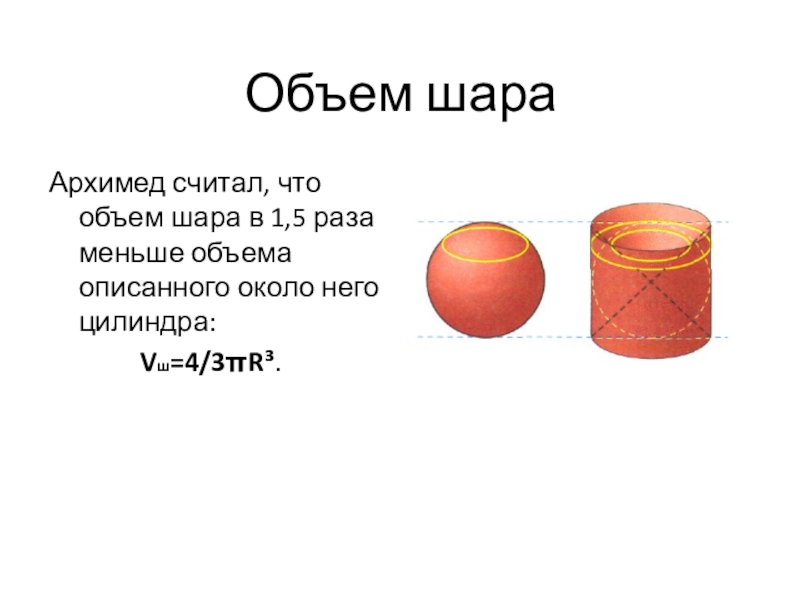
![Тела вращения
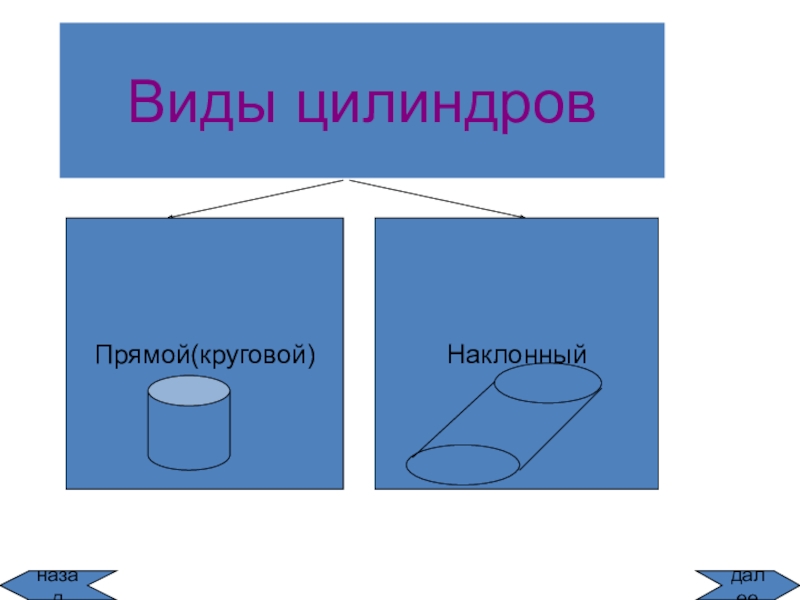
цилиндр
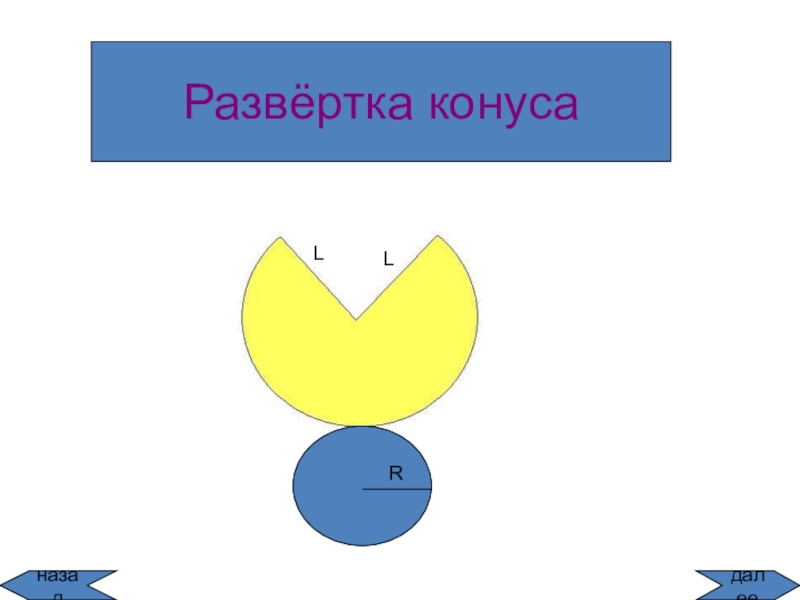
конус
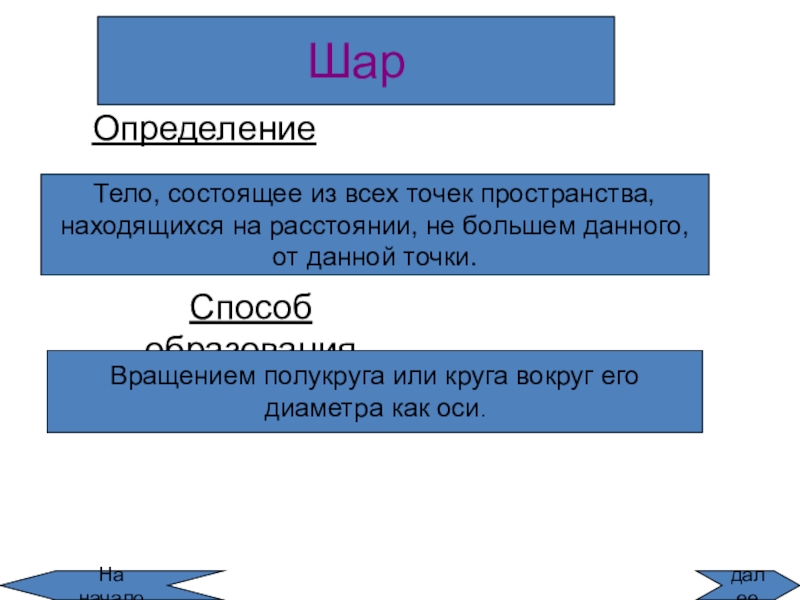
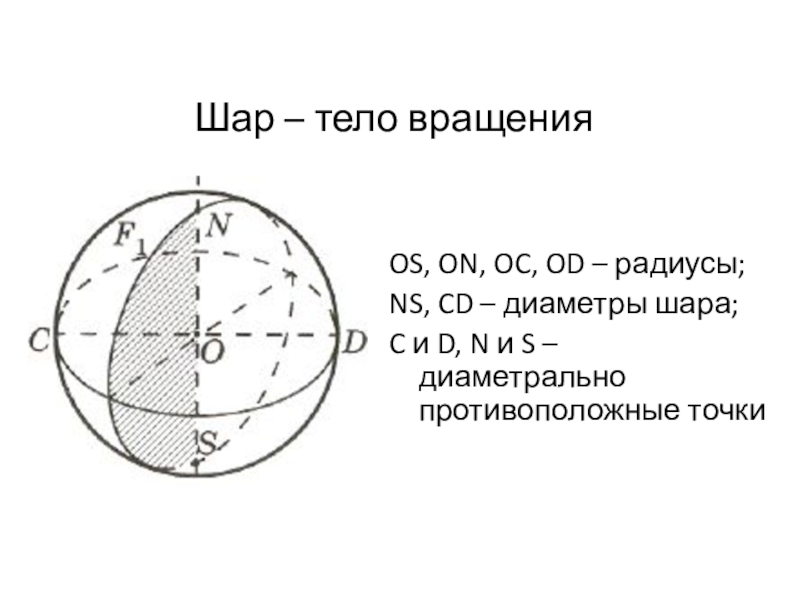
шар
далее
назад Как Архимед находил объем шараПлощади сечений: Sц, Sш, Sк.Sц=4πR²;Sш=π[CE]², где [CE]²=[EO]²-[OC]²=R²- -(x-R)²=2Rx-x²;Sк=π[CD]²= πx² Как Архимед находил объем шараПлощади сечений: Sц, Sш, Sк.Sц=4πR²;Sш=π[CE]², где [CE]²=[EO]²-[OC]²=R²- -(x-R)²=2Rx-x²;Sк=π[CD]²= πx²](/img/tmb/7/649864/715883338c82185231714ec30e711090-800x.jpg)