Тема

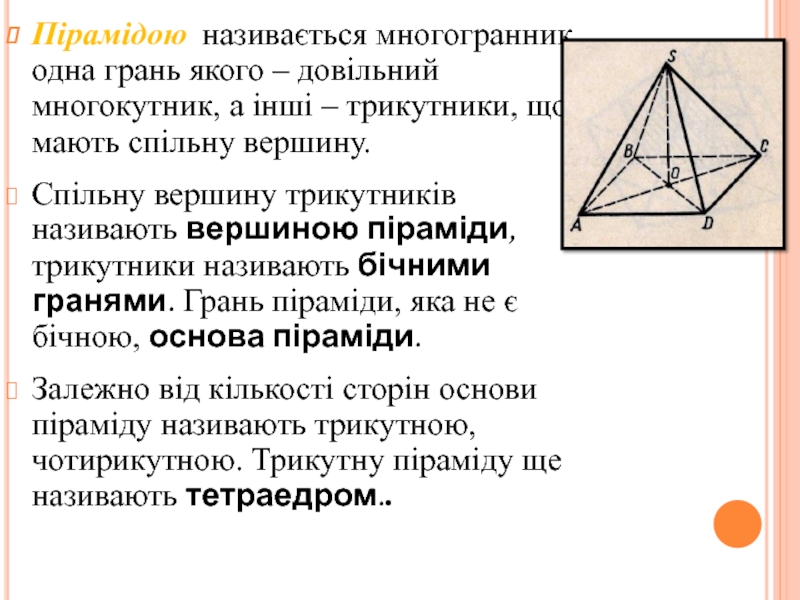
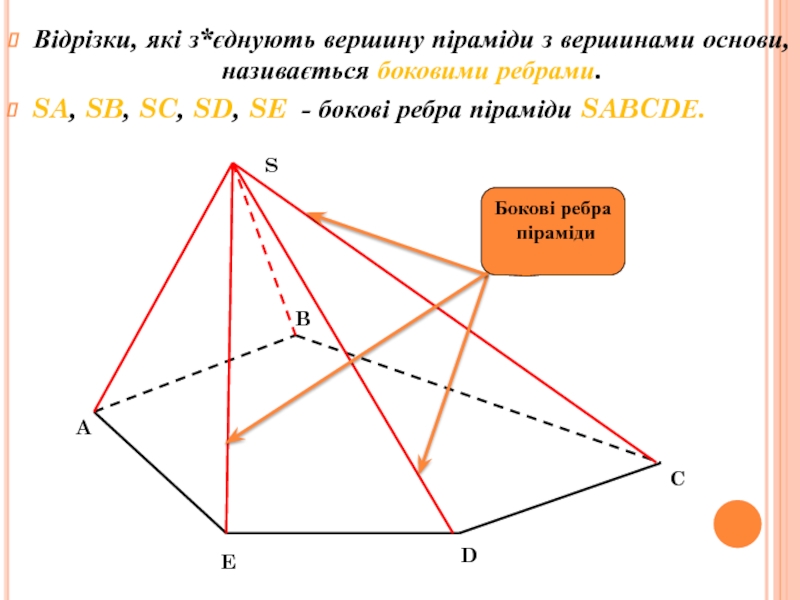
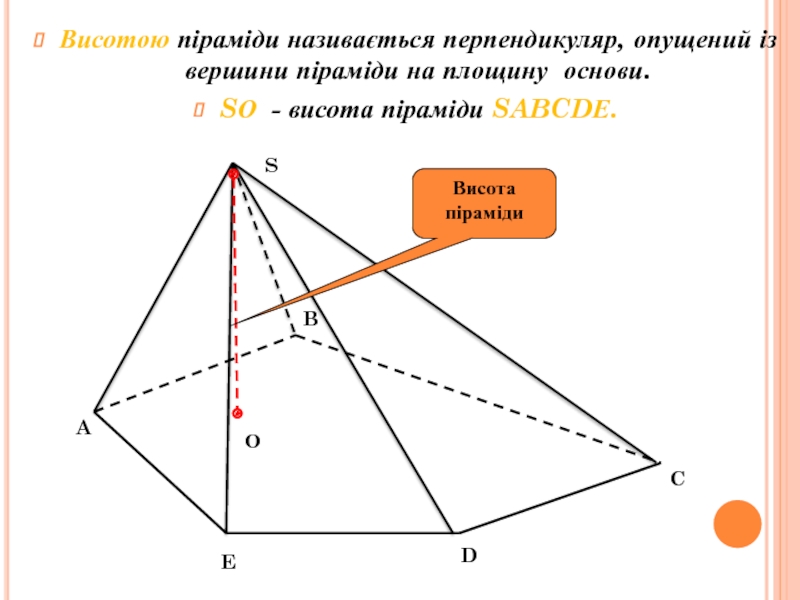
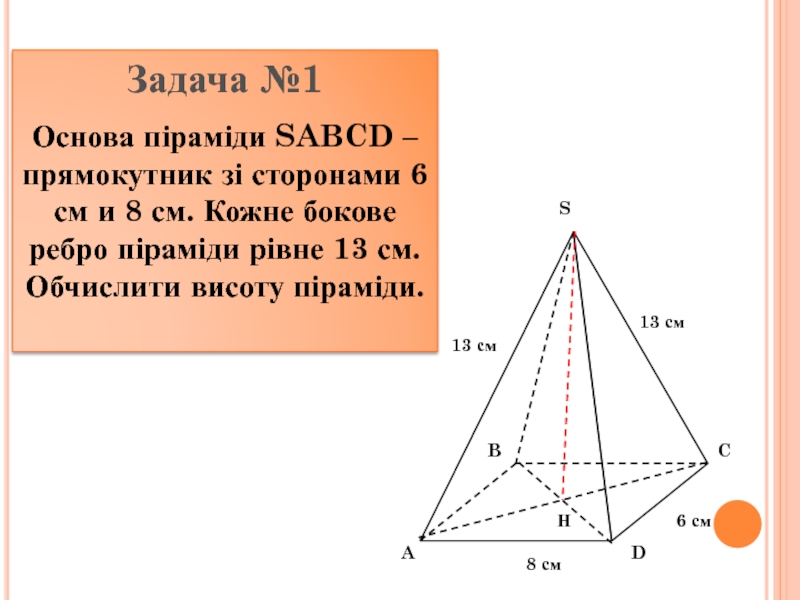
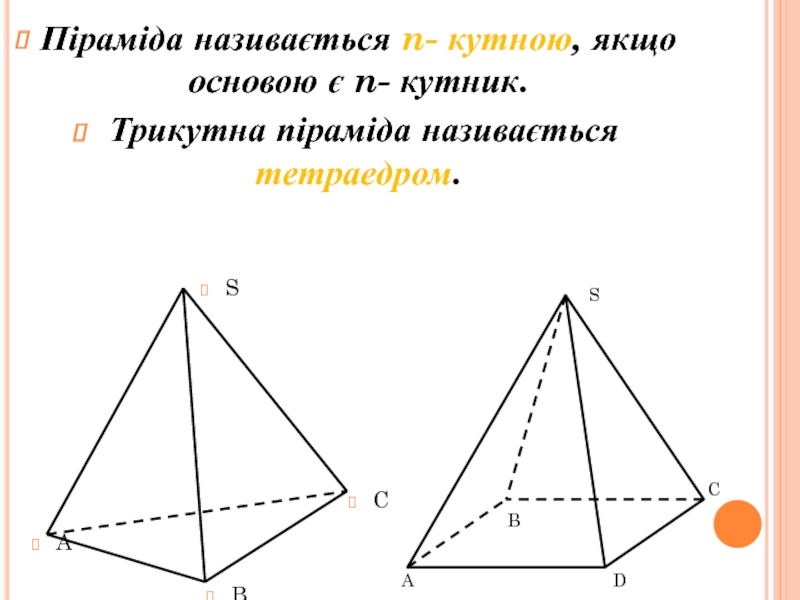
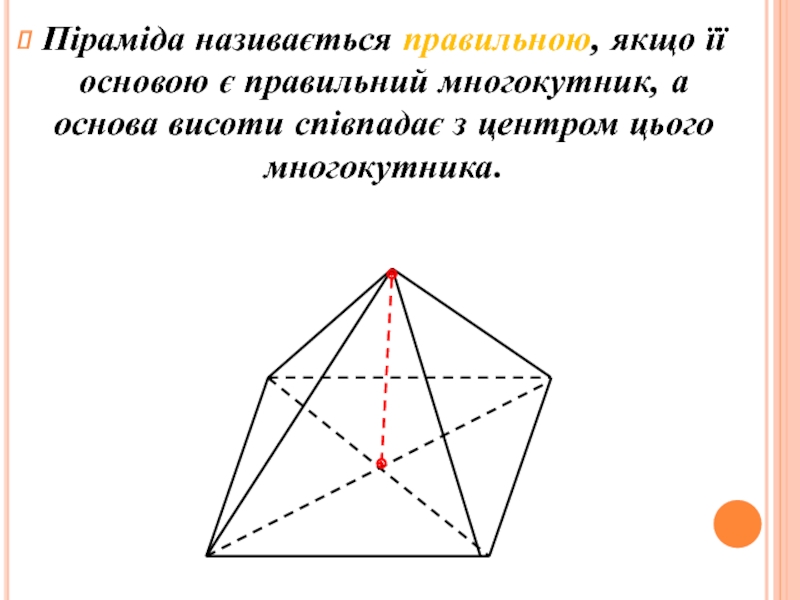
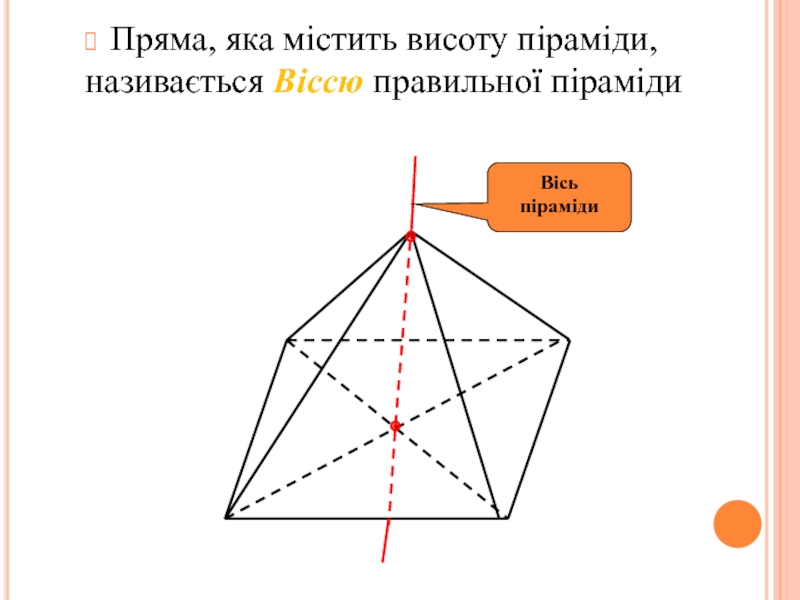
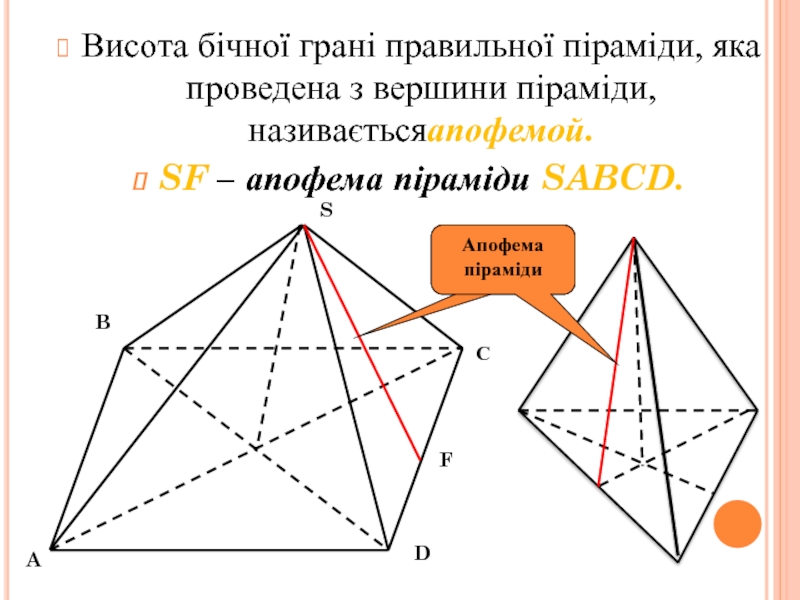
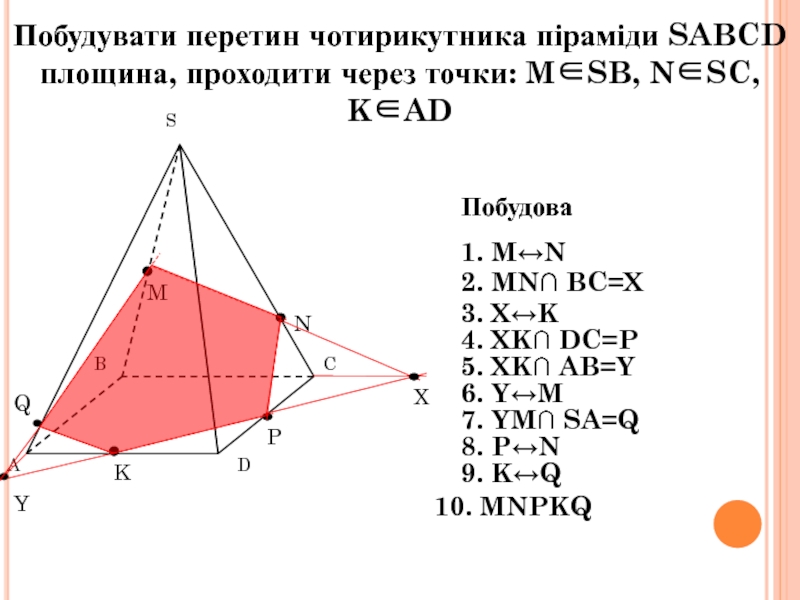
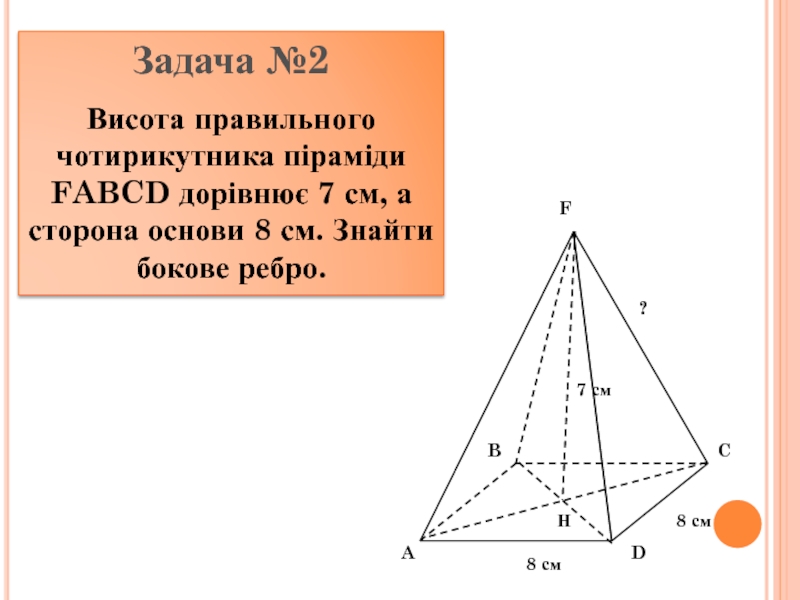
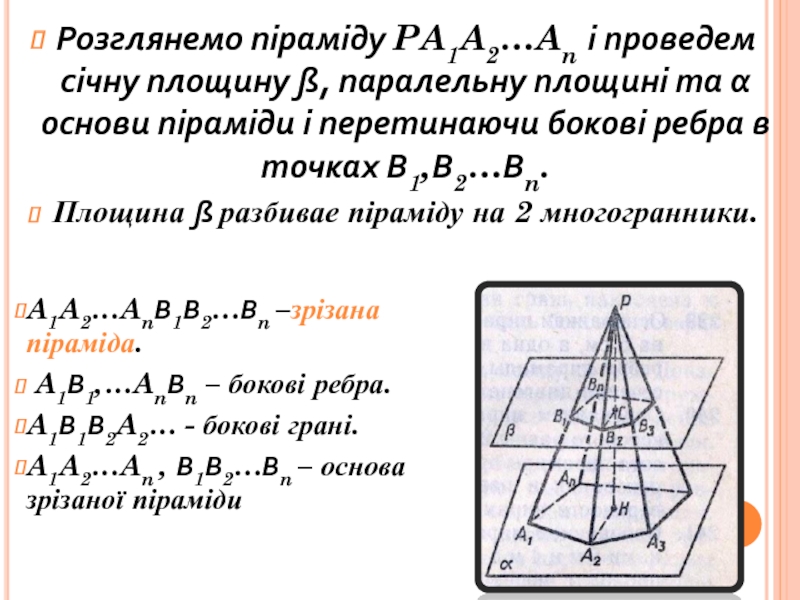
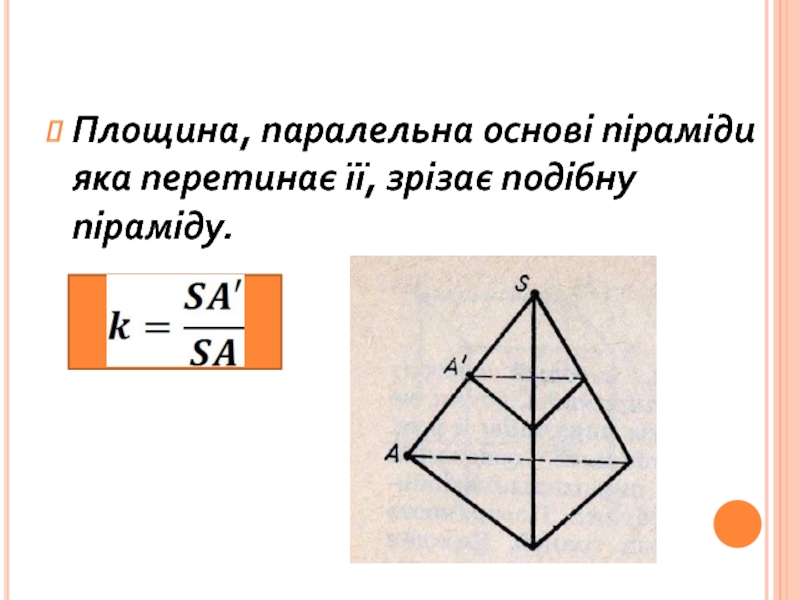
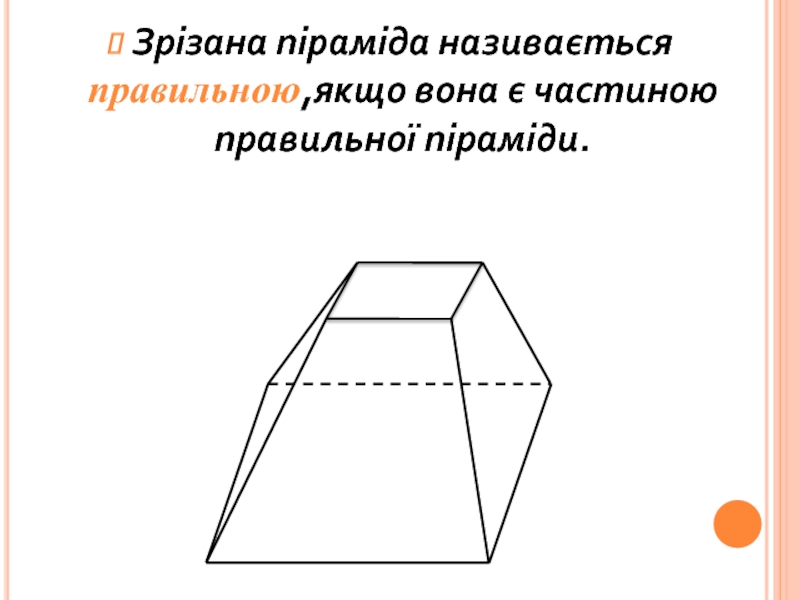
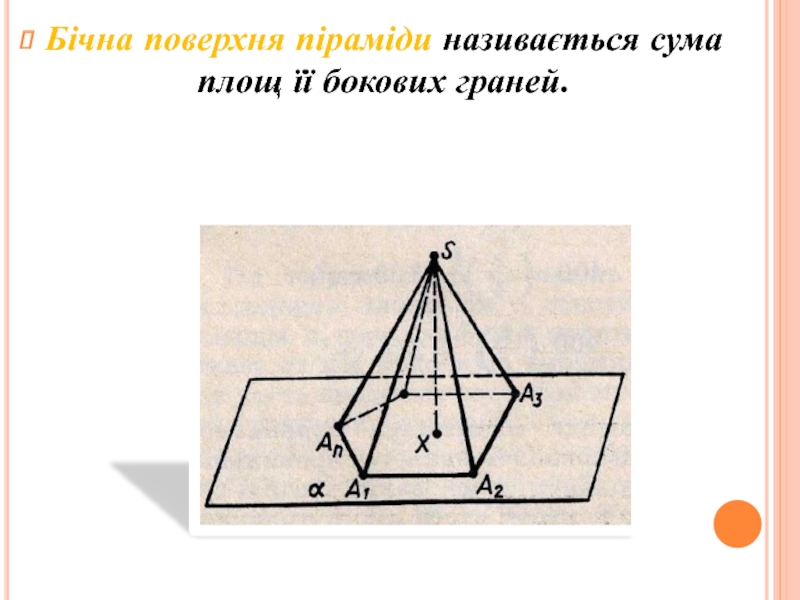
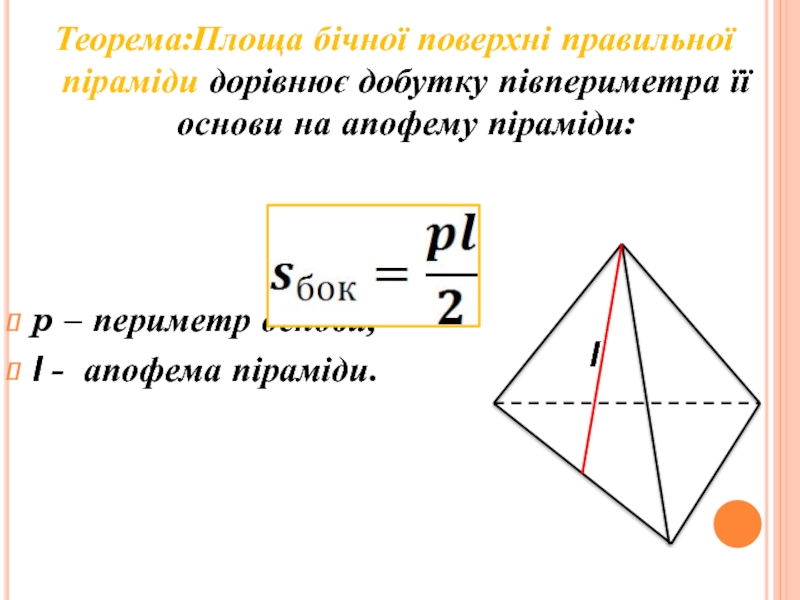
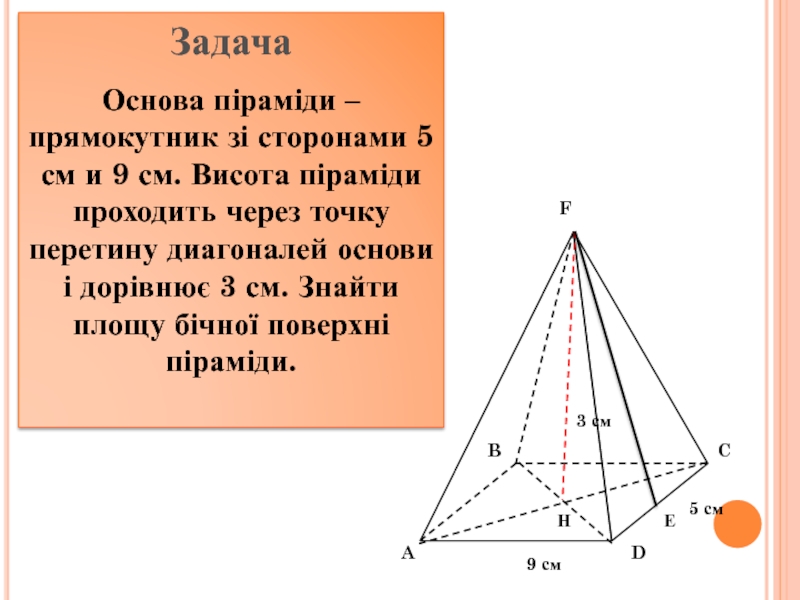
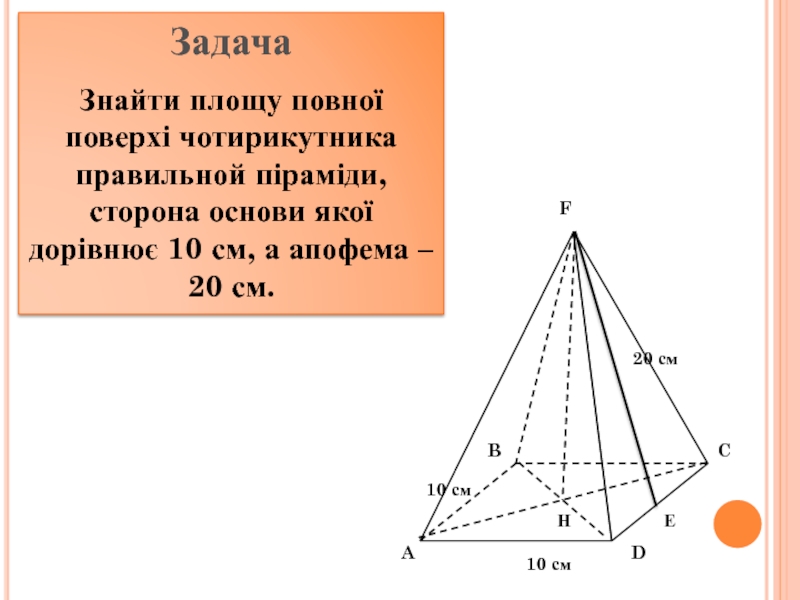
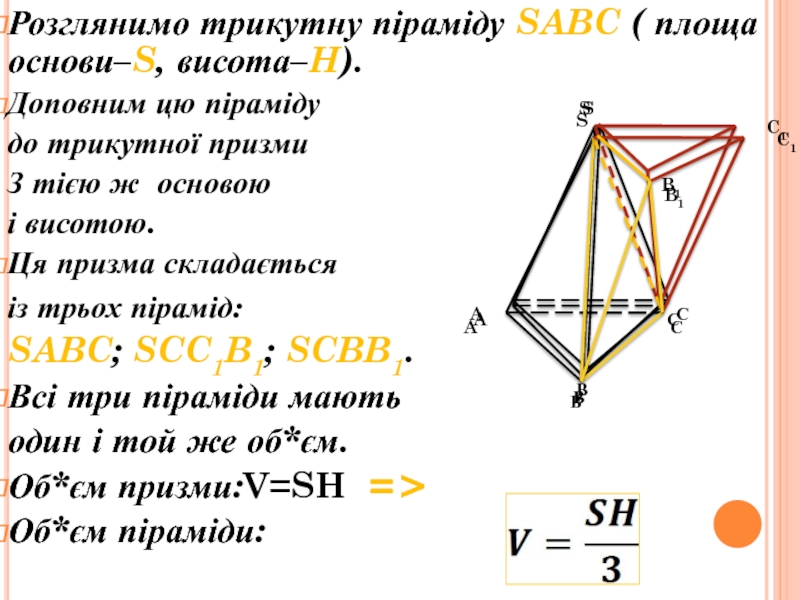
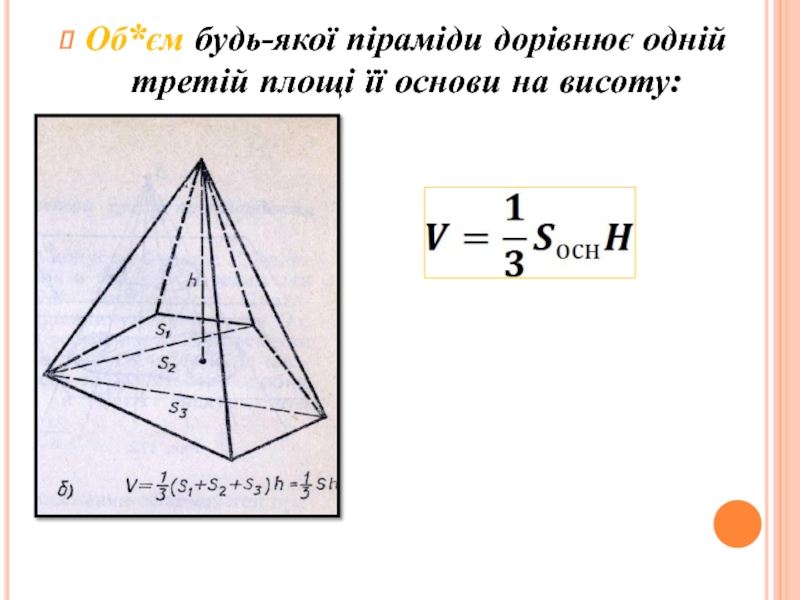
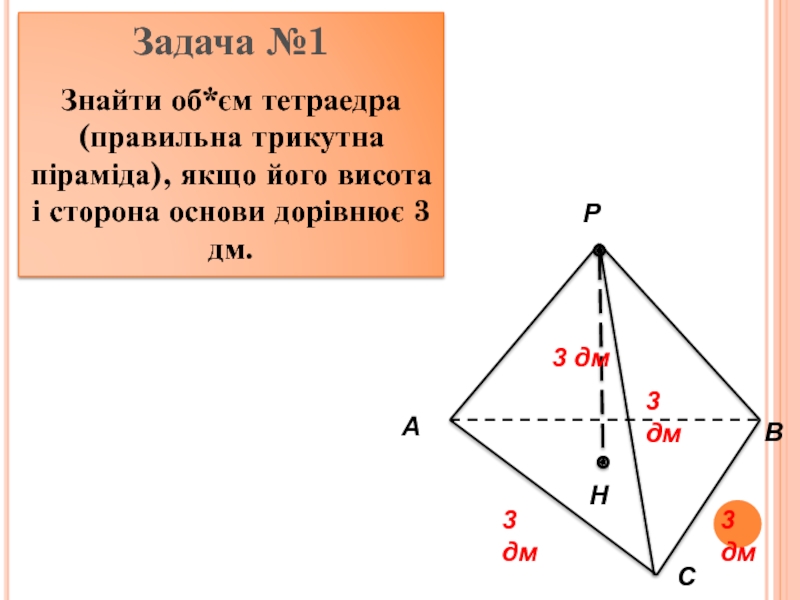
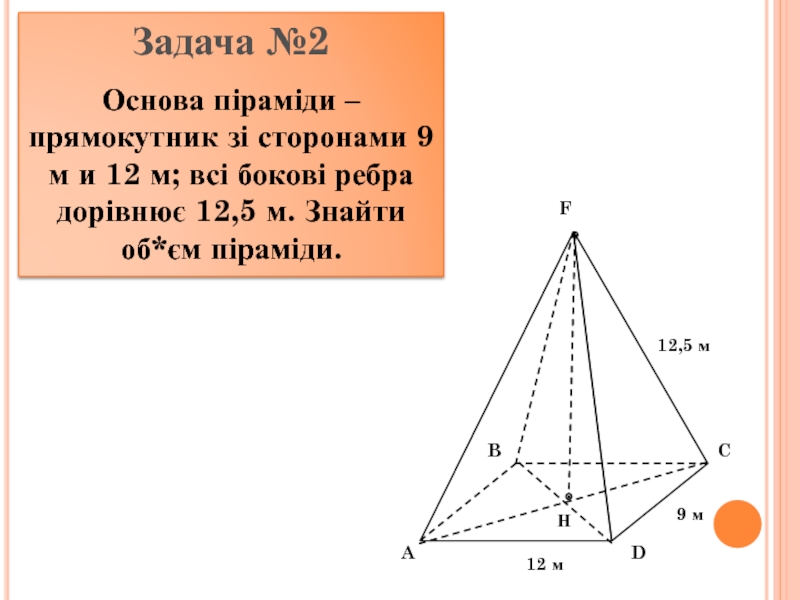
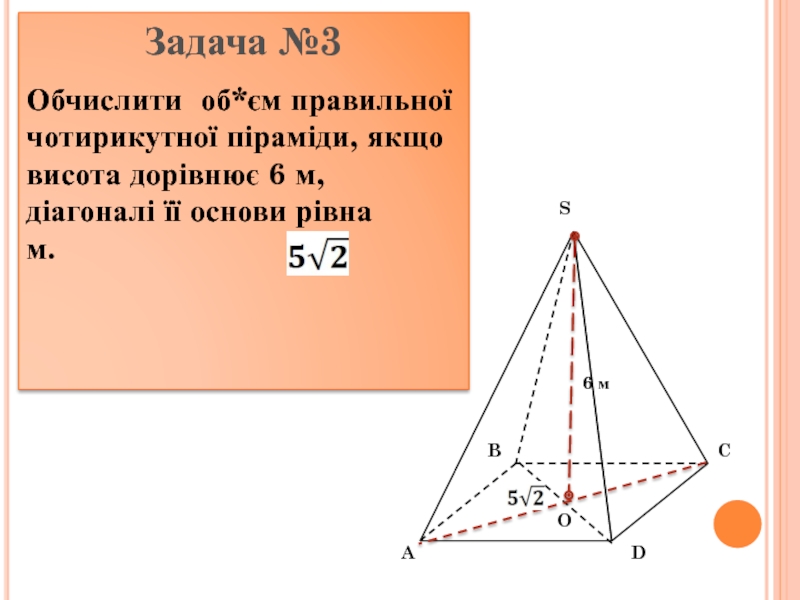
інші – трикутники, що мають спільну вершину.
Спільну вершину трикутників називають

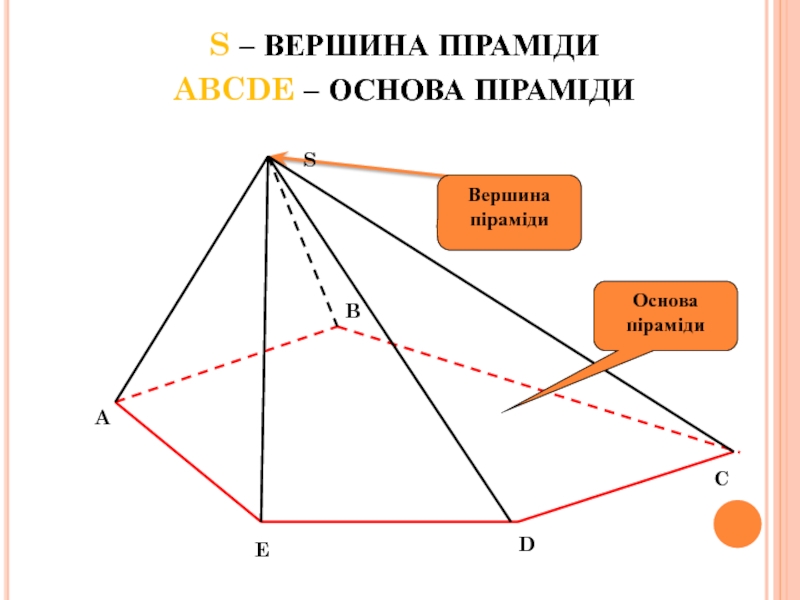
вершиною піраміди, трикутники називають бічними гранями. Грань піраміди, яка не є бічною, основа піраміди.
Залежно від кількості сторін основи піраміду називають трикутною, чотирикутною. Трикутну піраміду ще називають тетраедром..

яким греки називали єгипетські
піраміди; це слово походить від
давньоєгипетського

слова “пурама”,
яким ці піраміди називали
самі єгиптяни. Сучасні єгиптяни називають піраміди словом “ахрам”, яке також походить
від давньоєгипетського слова.

одна із «семи чудес світа» — піраміда Хеопса. Піраміди представляют

собой велику кам”яну споруду пірамідної форми, використовувалися в якості гробниці для фараонів Давнього Египта.
Всего в Египті було знайдено 118 пірамід.

Єгипетські піраміди

насип під кутом 15°. Довжину насипу збільшували зі збільшенням розмірів

піраміди. По цім насипам кам’яні блоки тягнули на дерев’яних санях, а щоб зменшити силу тертя, трасу постійно поливали водою. Потім з допомогою дерев’яних важелів блоки встановлювали на місце. Коли будівництво в основному закінчувалося, насип вирівнювали, а поверхню піраміди закривали спеціальними блоками.

Якість праці будівників, які жили ще 47 століть тому, була такою, що незбіг горизонтальних і вертикальних ліній піраміди не більше ширини великого пальця. Камені так тісно приєднувались один до одного, що між ними не можна було всунути навіть голку.

Будівництво пірамід

області.

ребрами.
SA, SB, SC, SD, SE - бокові ребра піраміди

SABCDЕ.

Бокові ребра
піраміди

основи.
SО - висота піраміди SABCDЕ.
О
Висота піраміди

и 8 см. Кожне бокове ребро піраміди рівне 13 см.

Обчислити висоту піраміди.

піраміда називається тетраедром.
C

основа висоти співпадає з центром цього многокутника.

називаєтьсяапофемой.
SF – апофема піраміди SABCD.
Апофема пирамиды
Апофема піраміди

NSC, KAD
Побудова
1. MN
2. MN BC=X
3. XK
4. XK DC=P
5. XK AB=Y
6.

YM

7. YM SA=Q

8. PN

9. KQ

10. MNPKQ

сторона основи 8 см. Знайти бокове ребро.

та α основи піраміди і перетинаючи бокові ребра в точках

В1,В2…Вn.
Площина ß разбивае піраміду на 2 многогранники.

A1A2…AnВ1В2…Вn –зрізана піраміда.
A1В1,…AnВn – бокові ребра.
A1В1В2A2… - бокові грані.
A1A2…An , В1В2…Вn – основа зрізаної піраміди

на апофему піраміди:



p – периметр основи;
l - апофема піраміди.

її основ на апофему:




p1 и p2 – периметри основ;
l

- апофема піраміди.

см. Висота піраміди проходить через точку перетину диагоналей основи і

дорівнює 3 см. Знайти площу бічної поверхні піраміди.

поверхні та площі основи:

дорівнює 10 см, а апофема – 20 см.

до трикутної призми
З тією ж основою
і висотою.
Ця призма

складається
із трьох пірамід:
SABC; SCC1B1; SCBB1.
Всі три піраміди мають
один і той же об*єм.
Об*єм призми:V=SH =>
Об*єм піраміди:

висоту:

висотою H :

і сторона основи дорівнює 3 дм.

12 м; всі бокові ребра дорівнює 12,5 м. Знайти об*єм

піраміди.

м, діагоналі її основи рівна

м.

і 8 см. Кожне бокове ребро піраміди дорівнює 13 см,

апофема – 12 см. Обчислити площу бокової поверхні, площу повної поверхні та об*єм піраміди.