Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 1. Описание структуры и свойств радиоматериалов (элементы
Содержание
- 1. Тема 1. Описание структуры и свойств радиоматериалов (элементы
- 2. Блок связей основных понятий и определений СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 3. Зависимость полной потенциальной энергии связи двух атомов
- 4. Значения энергий химической связи для некоторых элементов, эВ/атСПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 5. Криста́ллы (от греч. κρύσταλλος первоначально «лёд») —
- 6. : В зависимости от соотношения модулей базисных векторов,
- 7. РЕШЕТКИ БРАВЕ — 14
- 8. Cимметрия кристаллов ( элементарной ячейки)Симметричные (инвариантные) преобразования
- 9. Cимметрия кристаллов на примере кубической элементарной ячейкиСПбГЭТУ
- 10. Структура NaCl: ГЦК {Na[[0,0,0]; Cl[[0,5;0,5;0,5]]}Выбор (построение) элементарной
- 11. Как получаются сложные и разные кристаллические структуры? СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 12. а) ОЦК - объемноцентрированная кубическаяб) ГЦК —
- 13. Структура графена. Слой графита толщиной в один атом Кристаллические структуры аллотропных модификаций углеродаСПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 14. BaTiO2СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 15. Индексы Миллера для индицирования плоскости представляют собой
- 16. Задача 1.3. Записать матричное представление оси второго порядка, параллельно оси Z.Матрицы элементов симметриигде :
- 17. Теоремы о сочетании элементовСимметрии:Точка пересечения четной оси
- 18. 32КлассаСимметриикристаллов
- 19. Слайд 19
- 20. Принцип суперпозиции Кюрипринцип, согласно которому кристалл под
- 21. Блок- схема связей между предельными группами КюриСПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 22. Принцп суперпозиции КюриОдноосное растяжение-сжатиеСПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
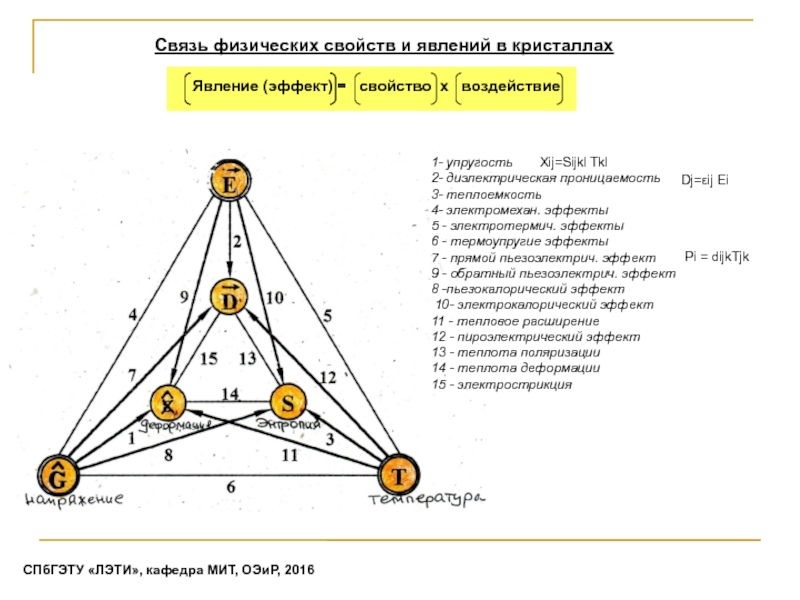
- 23. Связь физических свойств и явлений в кристаллахСПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 24. Dj=εij Ei, где: ij =1,2,3Симметрия физических
- 25. Класс симметрии 32, а=4,9138 с=5,4052,
- 26. Расположение ионов кислорода и кремния в кристалле кварцаСПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 27. Пьезоэлектрический эффектР- поляризацияТ- механические напряженияМатрица
- 28. Срезы кварцаАнизотропия свойств кристаллаСПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
- 29. Скачать презентанцию
Слайды и текст этой презентации
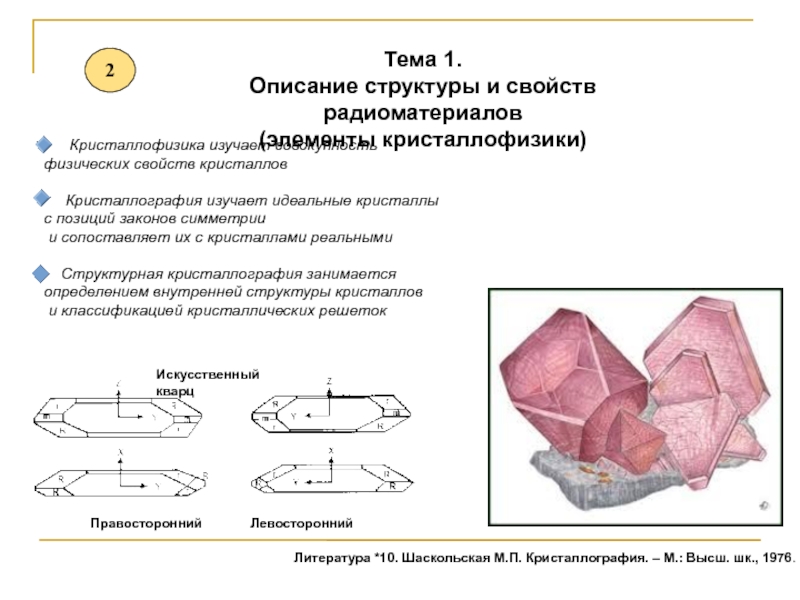
Слайд 1Тема 1.
Описание структуры и свойств радиоматериалов
(элементы кристаллофизики)
Литература *10. Шаскольская
М.П. Кристаллография. – М.: Высш. шк., 1976.
Слайд 3Зависимость полной потенциальной энергии связи
двух атомов от расстояния между
ними
Величина энергии связи определяется:
· притяжением атомов, обусловленным взаимодействием валентных
электронов;· кулоновским отталкиванием внутренних оболочек и ядер.
Зависимость силы взаимодействия ионов Na+ и Cl–,
показывающая равновесное состояние,
соответствующее длине связи ro = 0,28 нм
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
Слайд 4Значения энергий химической связи для некоторых элементов, эВ/ат
СПбГЭТУ «ЛЭТИ», кафедра
МИТ, ОЭиР, 2016
Слайд 5Криста́ллы (от греч. κρύσταλλος первоначально «лёд») — твёрдые тела, в
которых атомы расположены закономерно, образуя трёхмерно-периодическую пространственную укладку — кристаллическую
решётку.Кристаллы — это твёрдые вещества, имеющие естественную внешнюю форму правильных симметричных многогранников, основанную на их внутренней структуре, то есть на одном из нескольких определённых регулярных расположений составляющих вещество частиц (атомов, молекул, ионов).
Современное определение кристалла дано Международным союзом кристаллографов (http://reference.iucr.org/dictionary/Crystal): Материал представляет собой кристалл, если он имеет преимущественно острую дифракционную картину
Кристалл —анизотропное трехмерное упорядоченное твердое тело, находящееся в термодинамическом равновесии с окружающей средой
Слайд 6:
В зависимости от соотношения модулей базисных векторов, углов между ними
и положения узлов, все элементарные ячейки классифицируют по Браве.
По соотношению
между базисными векторами и углами, элементарные ячейки подразделяются на три категории: высшую, среднюю и низшую, и 7 сингоний:
Кубическая a= b= c , α=β=γ=90 град,
Тетрагональная a= b≠ c , α=β=γ=90 град,
Ромбическая a ≠ b ≠ c , α=β=γ=90 град,
Гексагональная a= b≠ c , α=β=90 град, γ=60 град,
Ромбоэдрическая (тригональная)
Моноклинная a ≠ b ≠ c , α=β=90 град, γ-любой,
Триклинная a ≠ b ≠ c , α,β,γ -любые
Слайд 7 РЕШЕТКИ БРАВЕ
— 14 различных типов пространственных
решеток, на которые подразделяются все возможные кристаллические решетки кристаллов
СПбГЭТУ
«ЛЭТИ», кафедра МИТ, ОЭиРМ, 2013Примитивная система трансляций P состоит из множества векторов
(a, b, c)
В объёмноцентрированную систему трансляций Браве J входит четыре вектора
(a, b, c, ½(a+b+c))
В гранецентрированную F — шесть векторов
(a, b, c, ½(a+b), ½(b+c), ½(a+c))
Базоцентрированные системы трансляций содержат по четыре вектора:
A — вектора (a, b, c, ½(b+c))
B — вектора (a, b, c, ½(a+c))
C — (a, b, c, ½(a+b)),
центрируя одну из граней элементарного объёма
Система трансляций Браве
Слайд 8Cимметрия кристаллов ( элементарной ячейки)
Симметричные (инвариантные) преобразования над точкой (фигурой):
*трансляция,
вектор трансляции; (a,b,c)
*поворот, поворотная ось n-го ранга, угол поворота (Ln)
отражение
относительно:* плоскости, плоскость симметрии (P,m)
* точки центр симметрии (C)
Рассматривая симметрию прямой тетрагональной призмы, выявляем (рис. 1.1) наличие осей 2, 3, 4, 6 порядка (возможных в твердом теле). В нашем случае есть четыре оси L2 ось L4, нет осей 3 и 6 порядка.
Рис. 1.1
Кроме того, у тетрагональной призмы есть горизонтальная плоскость симметрии P1, два семейства вертикальных взаимно перпендикулярных плоскостей симметрии P2, P3 и P4, P5 и центр симметрии
Все возможные сочетания имеющихся в кристаллической решётке поворотных осей симметрии и зеркальных плоскостей симметрии приводят к делению кристаллов на 32 класса симметрии, а с учётом винтовых осей симметрии и скользящих плоскостей симметрии на 230 пространственных групп.
Слайд 9Cимметрия кристаллов на примере кубической элементарной ячейки
СПбГЭТУ «ЛЭТИ», кафедра МИТ,
ОЭиР, 2018
Симметричные преобразования над кристаллическим многогранником образуют точечную группу и
объединяются в класс симметрии.Все элементы симметрии данного класса могут быть записаны формулой симметрии: например, для куба, имеющего 6 поворотных осей 2 порядка, 4 поворотные оси 3 порядка, 3 поворотных оси 4 порядка, 9 плоскостей симметрии и центр инверсии, формула симметрии:
Слайд 10Структура NaCl: ГЦК {Na[[0,0,0]; Cl[[0,5;0,5;0,5]]}
Выбор (построение) элементарной ячейки на примере
структуры NaCl: ГЦК {Na[[0,0,0]; Cl[[0,5;0,5;0,5]]}
+
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР,
2016Слайд 11Как получаются сложные и разные кристаллические структуры?
СПбГЭТУ «ЛЭТИ», кафедра
МИТ, ОЭиР, 2016
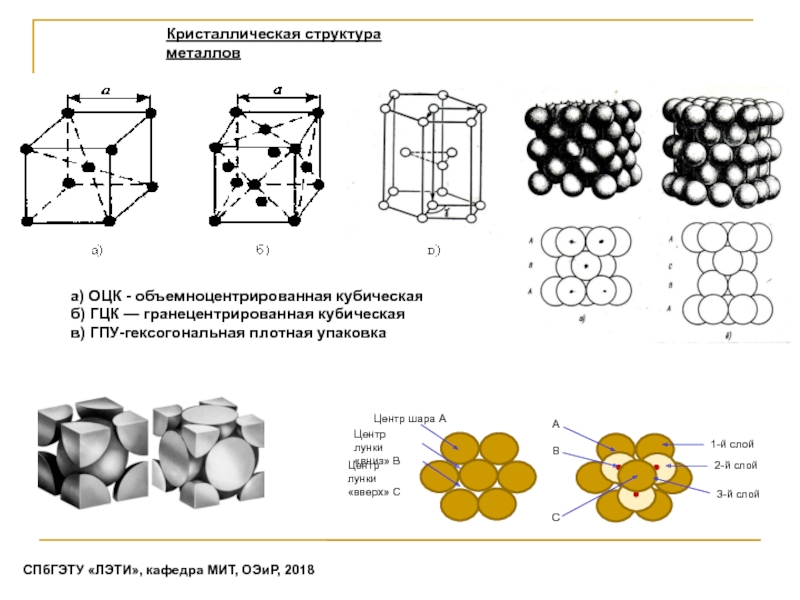
Слайд 12а) ОЦК - объемноцентрированная кубическая
б) ГЦК — гранецентрированная кубическая
в) ГПУ-гексогональная
плотная упаковка
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2018
Кристаллическая структура металлов
Слайд 13Структура графена. Слой графита толщиной в один атом
Кристаллические структуры аллотропных модификаций
углерода
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
Слайд 15Индексы Миллера для индицирования плоскости представляют собой коэффициенты в уравнении
плоскости, написанном в параметрическом виде; для нахождения индексов Миллера следует:
Индексами узла будет совокупность чисел n,l,m, записываемая [[n,l,m]].
За индексы направления (ребра) принимаются индексы ближайшего к началу координат узла, через которое проходит рассматриваемое направление, проведенное из начала координат [n,l,m].
Индицирование узлов, направлений и плоскостей в кристаллах
Если Т – радиус-вектор, проведенный из начала
координат в рассматриваемый узел
T= na +mb +lc , то
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
Слайд 16Задача 1.3. Записать матричное представление оси второго порядка, параллельно оси
Z.
Матрицы элементов симметрии
где
:
Слайд 17Теоремы о сочетании элементов
Симметрии:
Точка пересечения четной оси симметрии
с перпендикулярной ей
плоскостью
симметрии есть центр симметрии (Т2)
Шаскольская М.П. Кристаллография,
1984,стр.43
Слайд 20Принцип суперпозиции Кюри
принцип, согласно которому кристалл под внешним воздействием изменяет
свою точечную симметрию так,
что сохраняет лишь элементы симметрии, общие
с элементами симметрии воздействия. Принцип Неймана связывает симметрию свойств кристалла с симметрией кристалла до воздействия, в то время как принцип суперпозиции Кюри позволяет определить
симметрию кристалла после воздействия.
(1894г)
Принцип Неймана
постулат, устанавливающий связь симметрии макроскопических физических свойств кристалла с симметрией его внешней формы.
Согласно этому принципу, группа симметрии любого спонтанно присущего кристаллу физического свойства должна включать в себя операции симметрии точечной группы симметрии кристалла
Принципы кристаллофизики
Симметрия воздействия описывается
предельными классами симметрии Кюри
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
Слайд 24 Dj=εij Ei,
где: ij =1,2,3
Симметрия физических свойств и симметрия
структуры кристаллов
n=o, N=1 - скаляр, изотропная среда; симметрия сферы в
покоеn=1, N=3 – полярный вектор, анизотропная среда, симметрия конуса в покое и аксиальный вектор, симметрия вращающегося цилиндра;
n=2, N=9 – тензор 2-го ранга, анизотропная среда, симметрия цилиндра;
n=3, N=27- тензор 3-го ранга;
n=4, N=81- тензор 4-го ранга.
Число компонент тензора n-го ранга:
Pi = dijkTjk
Xij=Sijkl Tkl
Dj=εij Ei
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
Слайд 25Класс симметрии 32, а=4,9138 с=5,4052,
молекулярный вес 60,06,
плотность 2,649 г/см куб,
Тпл=1470 С, ТD=470 C,
ε11=4,58
ε33=4,71
d11 = 2,31 (10E-12)K/Н
d14 = 0,727
Xij=Sijkl Tkl
Pi = dijkTjk
Dj=εij Ei
Физические свойства кристаллов
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
Слайд 26 Расположение ионов кислорода
и кремния в кристалле
кварца
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016
Слайд 27Пьезоэлектрический эффект
Р- поляризация
Т- механические
напряжения
Матрица пьезомодулей
Pi = dijkTjk
Pi =di1 T1 + di2 T2 + di3 T3
+ di4 T4 + di5 T5 + di6 T6Pm = dmnTn,
где m=1,2,3, n=1,2,3,4,5,6
СПбГЭТУ «ЛЭТИ», кафедра МИТ, ОЭиР, 2016








![Тема 1.
Описание структуры и свойств радиоматериалов
(элементы Структура NaCl: ГЦК {Na[[0,0,0]; Cl[[0,5;0,5;0,5]]}Выбор (построение) элементарной ячейки на примере структуры Структура NaCl: ГЦК {Na[[0,0,0]; Cl[[0,5;0,5;0,5]]}Выбор (построение) элементарной ячейки на примере структуры NaCl: ГЦК {Na[[0,0,0]; Cl[[0,5;0,5;0,5]]}+СПбГЭТУ «ЛЭТИ»,](/img/thumbs/656ed099148d213a35527cfe10ea8170-800x.jpg)