Слайд 1Электродинамика и РРВ.Сем.1. Лекция 7.
Тема 3. ПЛОСКИЕ ЭМВ
В НЕОГРАНИЧЕННЫХ
СРЕДАХ
Лекция №7. Распространение плоских волн в гиротропных средах
Физические явления, возникающие
в ферритах при наличии подмагничивания. Резонансное поглощение
Особенности распространения ЭМВ в продольно намагниченном феррите.
Особенности распространения ЭМВ в поперечно намагниченном феррите.
Слайд 2Электродинамика и РРВ.Сем.1. Лекция 7.
1 Физические явления, возникающие в ферритах
при наличии подмагничивания. Резонансное поглощение
Ферриты, относящиеся к классу ферримагнетиков, представляют
собой соединения оксида железа с оксидами других металлов и обладают высоким большим (до Омм) электрическим сопротивлением.
Электродинамические свойства ферритов зависят от частоты, но изменяются в различных пределах.
В диапазоне СВЧ на сантиметровых волнах величина относительной магнитной проницаемости приближенно равна единице.
Рабочий диапазон частот ферритов ‑ от 20МГц до 150ГГц. Для работы на разных частотах используются различные материалы.
Слайд 3Электродинамика и РРВ.Сем.1. Лекция 7.
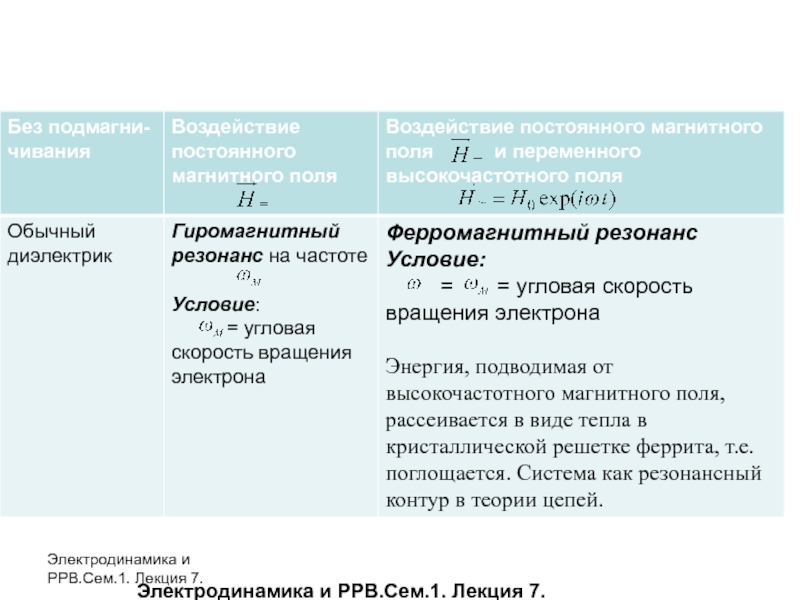
В ненамагниченном состоянии ферриты - обычный
диэлектрик.
При воздействии постоянного магнитного поля возникает прецессия вокруг исходного положения
оси вращения электрона.
Частота прецессии (частота гиромагнитного резонанса) зависит от
величины постоянного магнитного поля ;
гиромагнитного отношения [Гц/(Ам)], связывающего заряд и массу электрона:
и соответствует угловой скорости вращения электрона.
При воздействии еще и переменного высокочастотного поля
ось вращения электрона будет отклоняться, если переменное магнитное поле будет действовать перпендикулярно оси вращения.
Слайд 4Электродинамика и РРВ.Сем.1. Лекция 7.
Электродинамика и РРВ.Сем.1. Лекция 7.
Слайд 5Электродинамика и РРВ.Сем.1. Лекция 7.
Математическое описание явлений в феррите отражается
в тензорной записи магнитной проницаемости:
где
, ,
,
- магнитная восприимчивость среды.
Ферромагнитный резонанс возникает, когда (в нуль обращается знаменатель).
Слайд 6Электродинамика и РРВ.Сем.1. Лекция 7.
2 Особенности распространения ЭМВ
в
продольно намагниченном феррите
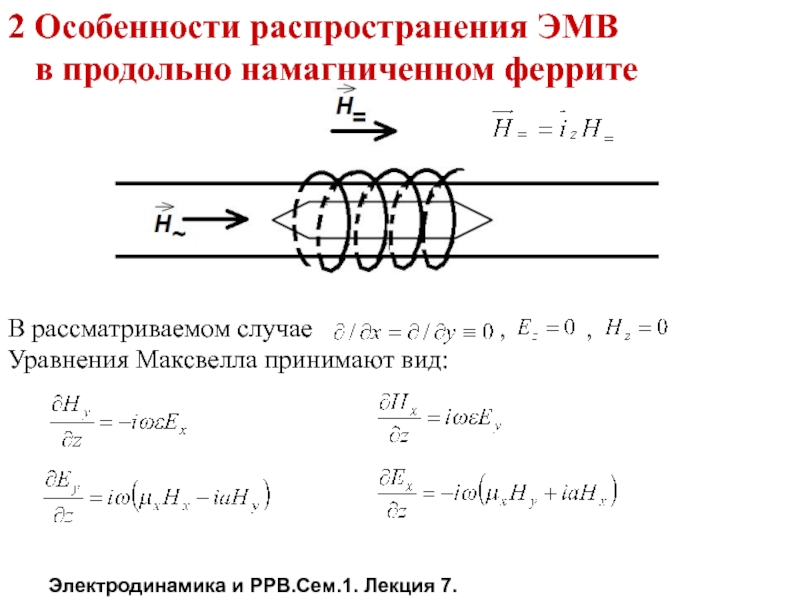
В рассматриваемом случае
, ,
Уравнения Максвелла принимают вид:
Слайд 7Электродинамика и РРВ.Сем.1. Лекция 7.
Решение уравнений Максвелла:
- волновое число
;
- волновое сопротивление среды .
Индекс «1» соответствует волне круговой поляризации с левым направлением вращения, индекс «2» – волне с правым направлением вращения.
Таким образом, волна линейной поляризации
представляется в виде суперпозиции двух волн
круговой поляризации.
Слайд 8Электродинамика и РРВ.Сем.1. Лекция 7.
Анализ структуры поля
1. Изменение поляризации волны.
Если
обе волны круговой поляризации имеют равные амплитуды на входе, то
компоненты суммарного ЭМП на выходе обладают следующими свойствами:
‑ суммарная компонента вектора напряженности магнитного поля сохраняют поляризацию исходной волны;
‑ электрическое поле суммарной волны становится эллиптически поляризованным, поскольку волновые сопротивления волн разные).
2. Эффект Фарадея.
Угол наклона вектора :
где - постоянная Фарадея.
Явление поворота поляризационного эллипса в зависимости от пройденного волной расстояния называется эффектом Фарадея.
Среды, в которых происходит данный эффект, называются гиротропными.
Слайд 9Электродинамика и РРВ.Сем.1. Лекция 7.
3. Различие фазовых скоростей волн с
левым и правым направлением вращения.
где
Следствие различия фазовых скоростей волн:
1) резонансное
поглощение при ферромагнитном резонансе испытывает волна правого направления вращения, индекс «2» (ее фазовая обращается в нуль);
2) изменением величины , т.е. постоянного магнитного поля, можно управлять параметрами феррита;
3) в ферритах конечных размеров в поперечном сечении наблюдается эффект смещения поля (при отрицательных значениях волновое число становится комплексным. В результате имеем волны с экспоненциально убывающей амплитудой вследствие эффекта вытеснения поля средой.
Слайд 10Электродинамика и РРВ.Сем.1. Лекция 7.
4. Феррит – невзаимная среда.
Вектор при
движении волны в прямом направлении поворачивается в положение B, а
при обратном – не возвращается в A, а, продолжая вращаться в ту же сторону, приходит в положение C.
Слайд 11Электродинамика и РРВ.Сем.1. Лекция 7.
3 Особенности распространения ЭМВ
в
поперечно намагниченном феррите
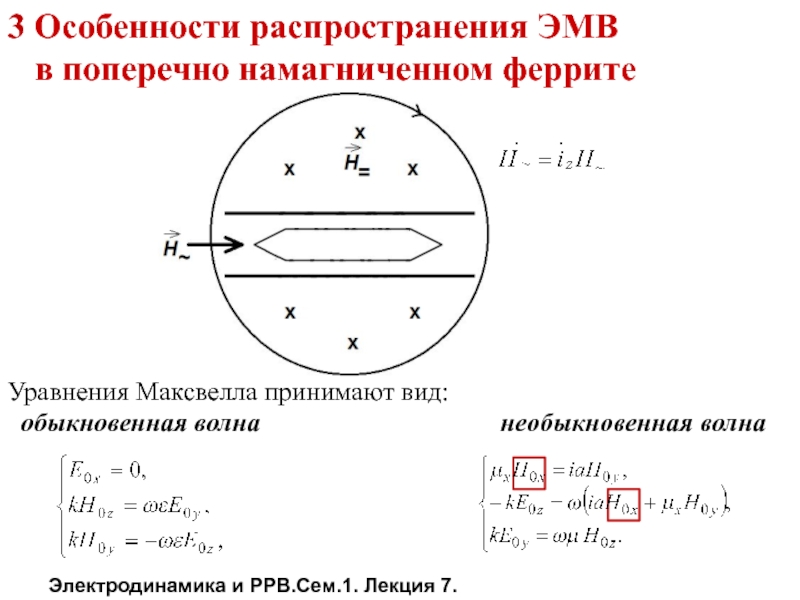
Уравнения Максвелла принимают вид:
обыкновенная волна
необыкновенная волна
Слайд 12Электродинамика и РРВ.Сем.1. Лекция 7.
Анализ структуры поля
Различие фазовых скоростей
для обыкновенной
волны ,
- для необыкновенной волны: ,
Следствия:
Возможность создания поперечного гиромагнитного резонанса для необыкновенной волны при , , ;
Условия возбуждения поперечного
и ферромагнитного резонансов:
1,2 - ;
3 - ;
4 -
2) Изменение поляризации суммарной волны при изменении пройденного расстояния (эффект Коттона-Мутона):