Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 3 Проекции плоскости понятия линейных геометрических образов, общие
Содержание
- 1. Тема 3 Проекции плоскости понятия линейных геометрических образов, общие
- 2. Кинематический способ образования плоскостиCDПлоскость может быть
- 3. Проекции плоскостиПри проецировании необходимо установить однозначное соответствие
- 4. Проекции плоскостиOПространственная картинаBСпособы определения(А, В, С)(m, В)Плоскость
- 5. Проекции плоскостиПространственная картинаBСпособы определения(А, В, С)(m, В)(m
- 6. Проекции плоскостиПространственная картинаСпособы определения(А, В, С)B(m, В)n(m
- 7. Способы задания плоскостиНа комплексном чертеже плоскость
- 8. Способы задания плоскости5) проекциями плоской фигурой; 6)
- 9. Положение плоскости относительно плоскостей проекцийПлоскость общего положения
- 10. Горизонтально проецирующая плоскость (П1)Пространственная картинаКомплексный чертежyzГоризонтальная проекция
- 11. Фронтально проецирующая плоскость (П2)Комплексный чертежyzПространственная картинаФронтальная проекция
- 12. Профильно проецирующая плоскость (П3)Комплексный чертежzПространственная картинаПрофильная проекция
- 13. Горизонтальная плоскость уровня ( П1)Комплексный чертежzПространственная картинаВ
- 14. Фронтальная плоскость уровня ( П2)Комплексный чертежzПространственная картинаВ
- 15. Профильная плоскость уровня ( П3)Комплексный чертежzПространственная картинаВ
- 16. Принадлежность прямой плоскостиПрямая принадлежит плоскости, если она
- 17. Принадлежность точки плоскостиТочка будет лежать в плоскости,
- 18. Принадлежность прямой и точки плоскости(1 , 2)xA1
- 19. Принадлежность прямой и точки плоскостиЕсли плоскость занимает
- 20. Главные линии плоскостиГоризонталь плоскости – это прямая,
- 21. Главные линии плоскостиФронталей плоскости бесчисленное множество,все они
- 22. Главные линии плоскостиx П1x П2xФронтальная
- 23. Главные линии плоскостиx П1x П2xВ
- 24. Следы плоскостиНайдем горизонтальный – N и фронтальный
- 25. Сколько точек, не лежащих на одной прямой,
- 26. 3. Какая проекция плоскости общего положения
- 27. а) рис.? – горизонтально проецирующая б) рис.?
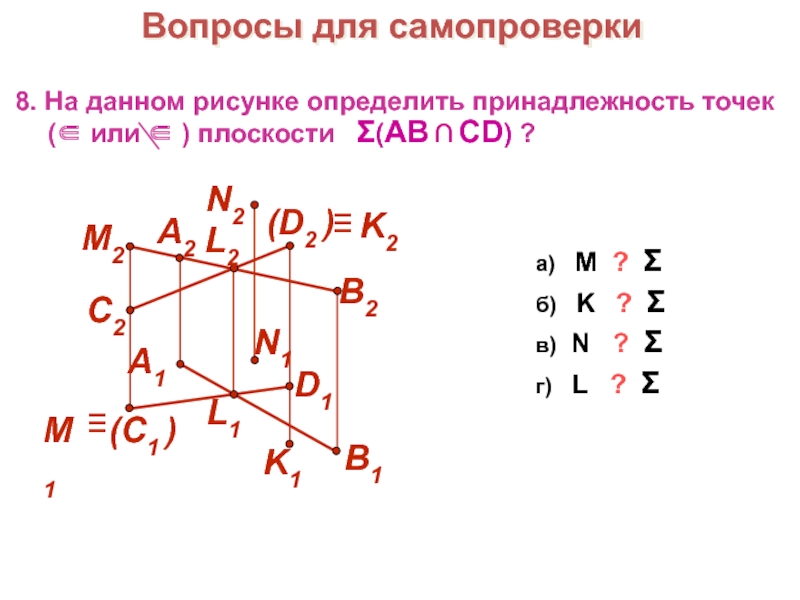
- 28. Вопросы для самопроверкиа) М ?
- 29. Вопросы для самопроверки
- 30. Вопросы для самопроверки10. Как можно назвать горизонтальный
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема 3
Проекции плоскости
понятия линейных геометрических образов, общие закономерности при проецировании
плоскостей, точечное соответствие
Слайд 2Кинематический способ образования плоскости
C
D
Плоскость может быть образована параллельным перемещением
прямой АВ (образующей) по неподвижной прямой СD (направляющей). Плоскость безгранична
и бесконечна, делит пространство на две частиАВ - образующая
CD - направляющая
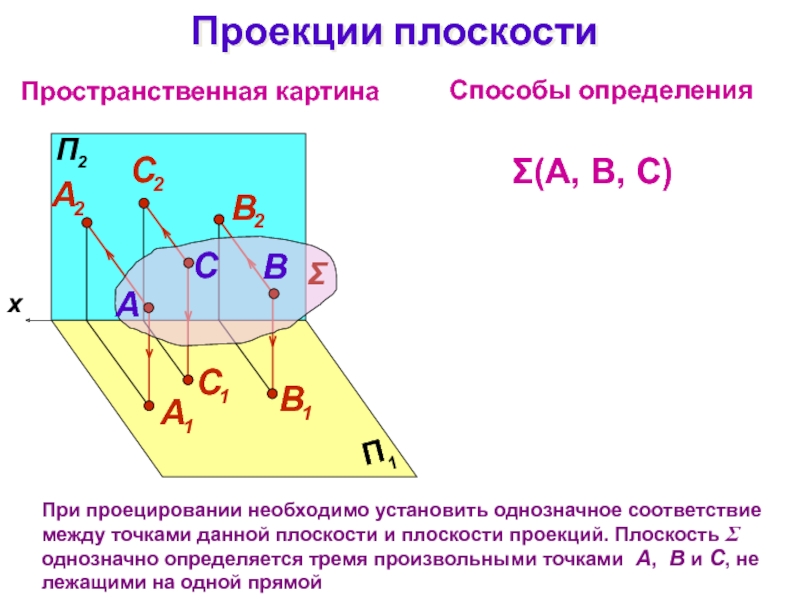
Слайд 3Проекции плоскости
При проецировании необходимо установить однозначное соответствие между точками данной
плоскости и плоскости проекций. Плоскость однозначно определяется тремя произвольными
точками А, В и С, не лежащими на одной прямойПространственная картина
Способы определения
(А, В, С)
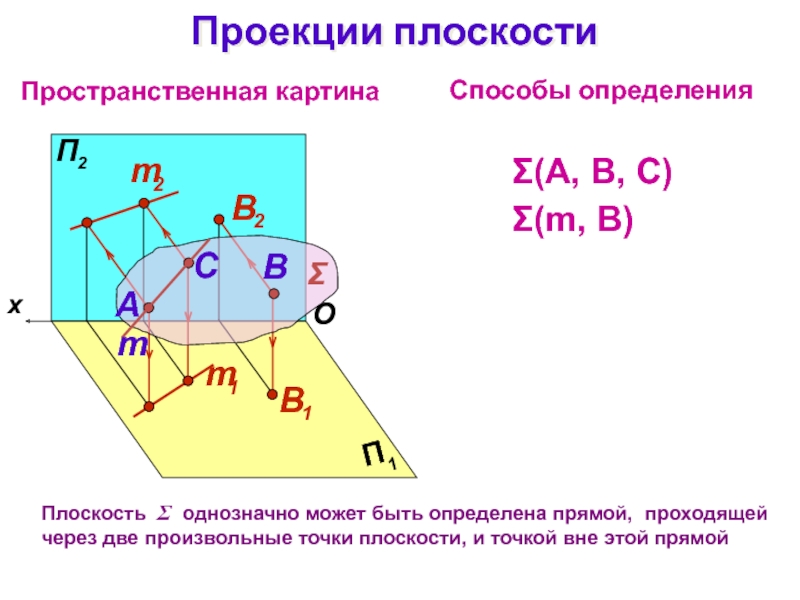
Слайд 4Проекции плоскости
O
Пространственная картина
B
Способы определения
(А, В, С)
(m, В)
Плоскость однозначно может
быть определена прямой, проходящей через две произвольные точки плоскости, и
точкой вне этой прямойСлайд 5Проекции плоскости
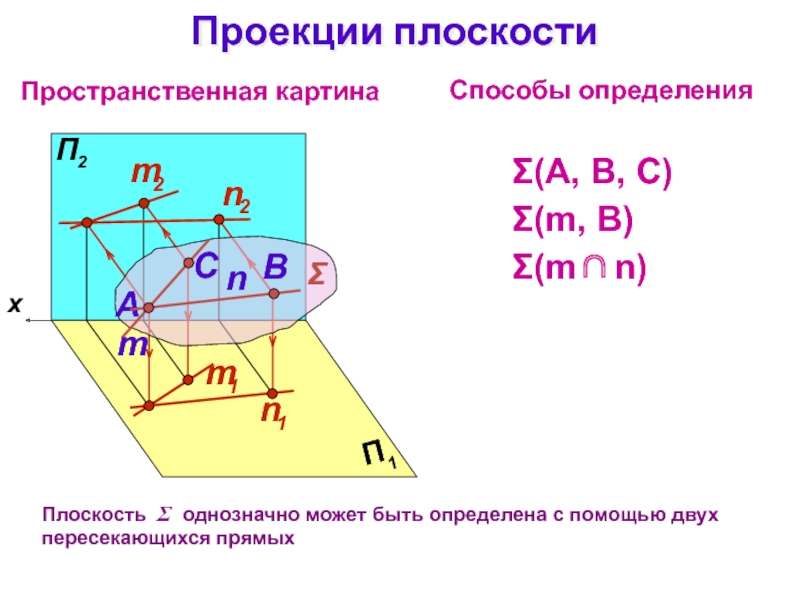
Пространственная картина
B
Способы определения
(А, В, С)
(m, В)
(m n)
Плоскость
однозначно может быть определена с помощью двух пересекающихся прямых
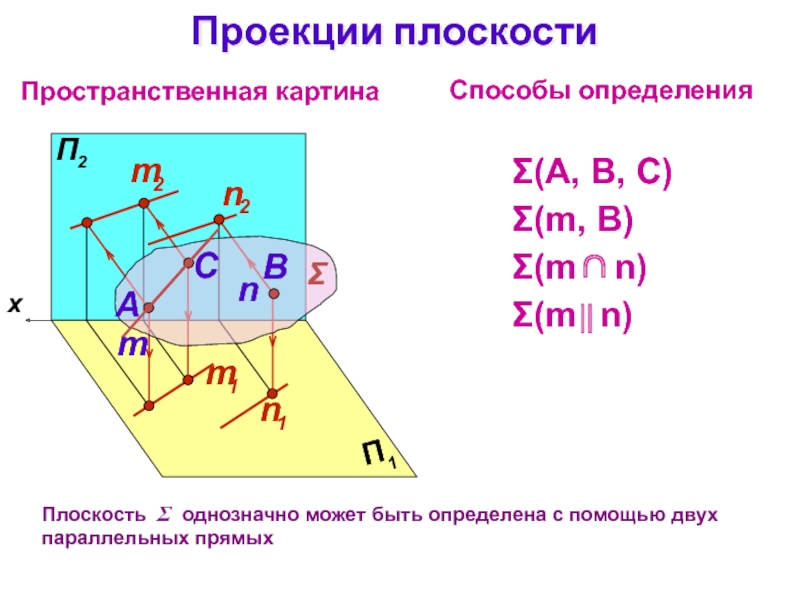
Слайд 6Проекции плоскости
Пространственная картина
Способы определения
(А, В, С)
B
(m, В)
n
(m n)
(m n)
Плоскость
однозначно может быть определена с помощью двух параллельных прямых
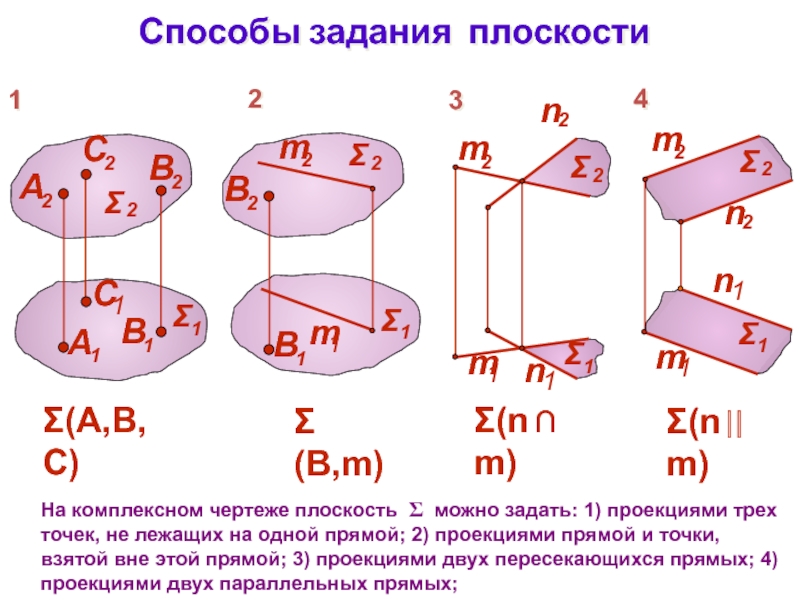
Слайд 7Способы задания плоскости
На комплексном чертеже плоскость можно задать: 1)
проекциями трех точек, не лежащих на одной прямой; 2) проекциями
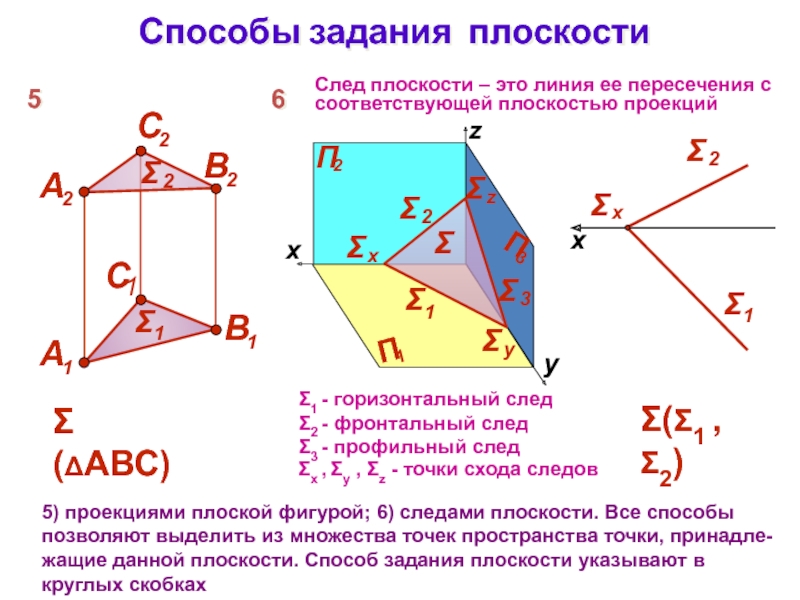
прямой и точки, взятой вне этой прямой; 3) проекциями двух пересекающихся прямых; 4) проекциями двух параллельных прямых;Слайд 8Способы задания плоскости
5) проекциями плоской фигурой; 6) следами плоскости. Все
способы позволяют выделить из множества точек пространства точки, принадле-жащие данной
плоскости. Способ задания плоскости указывают в круглых скобкахСлед плоскости – это линия ее пересечения с соответствующей плоскостью проекций
Слайд 9Положение плоскости относительно плоскостей проекций
Плоскость общего положения наклонена ко всем
плоскостям проекций
Плоскость частного положения перпендикулярна или параллельна одной из плоскостей
проекций Горизонтально проецирующая плоскость П1
Фронтально проецирующая плоскость П2 Профильно проецирующая плоскость П3
Горизонтальная плоскость П1
Фронтальная плоскость П2
Профильная плоскость П3
Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей плоскостью:
Плоскость, параллельная плоскости проекций, назы-вается плоскостью уровня (дважды проецирующей):
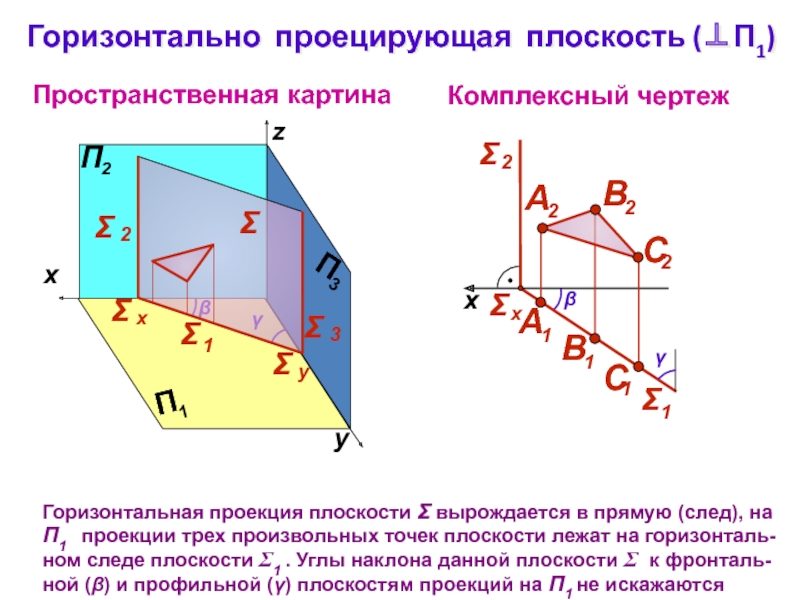
Слайд 10Горизонтально проецирующая плоскость (П1)
Пространственная картина
Комплексный чертеж
y
z
Горизонтальная проекция плоскости вырождается
в прямую (след), на П1 проекции трех произвольных точек
плоскости лежат на горизонталь-ном следе плоскости 1 . Углы наклона данной плоскости к фронталь-ной () и профильной () плоскостям проекций на П1 не искажаются
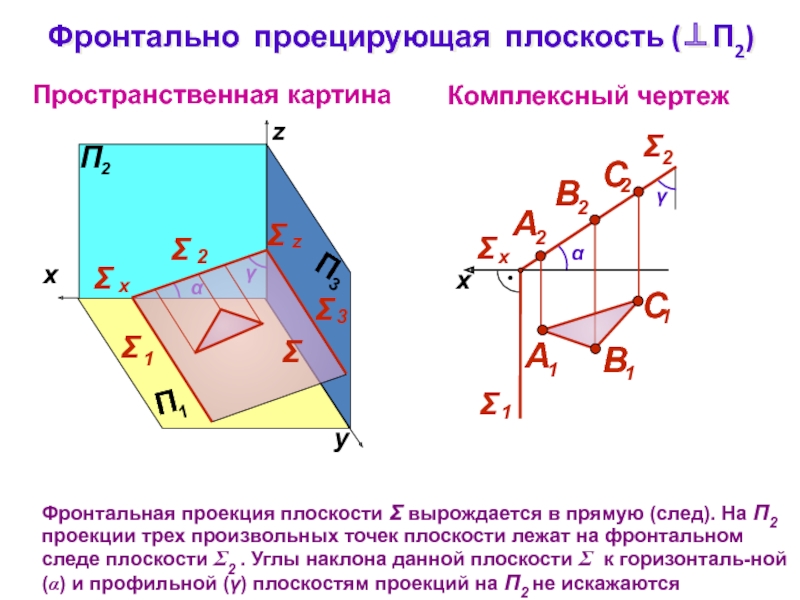
Слайд 11Фронтально проецирующая плоскость (П2)
Комплексный чертеж
y
z
Пространственная картина
Фронтальная проекция плоскости вырождается
в прямую (след). На П2 проекции трех произвольных точек плоскости
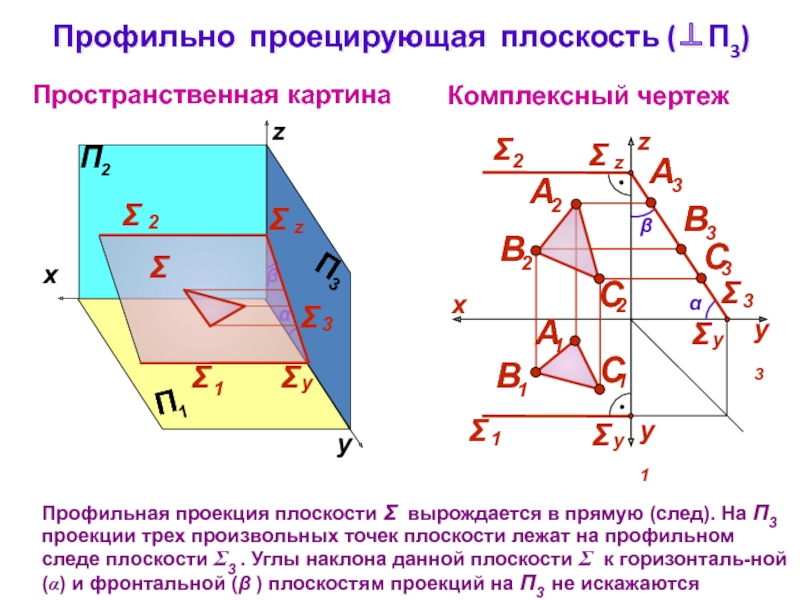
лежат на фронтальном следе плоскости 2 . Углы наклона данной плоскости к горизонталь-ной () и профильной () плоскостям проекций на П2 не искажаютсяСлайд 12Профильно проецирующая плоскость (П3)
Комплексный чертеж
z
Пространственная картина
Профильная проекция плоскости вырождается
в прямую (след). На П3 проекции трех произвольных точек плоскости
лежат на профильном следе плоскости 3 . Углы наклона данной плоскости к горизонталь-ной () и фронтальной ( ) плоскостям проекций на П3 не искажаютсяСлайд 13Горизонтальная плоскость уровня ( П1)
Комплексный чертеж
z
Пространственная картина
В силу параллельности следы
(фронтальный 2 и профильный 3 ) плоскости будут параллельны
соответствующим осям координат. Фигура, задающая плоскость , проецируется в натуральную величину на горизонтальную плоскость проекцийСлайд 14Фронтальная плоскость уровня ( П2)
Комплексный чертеж
z
Пространственная картина
В силу параллельности следы
(горизонтальный 1 и профильный 3 ) плоскости будут параллельны
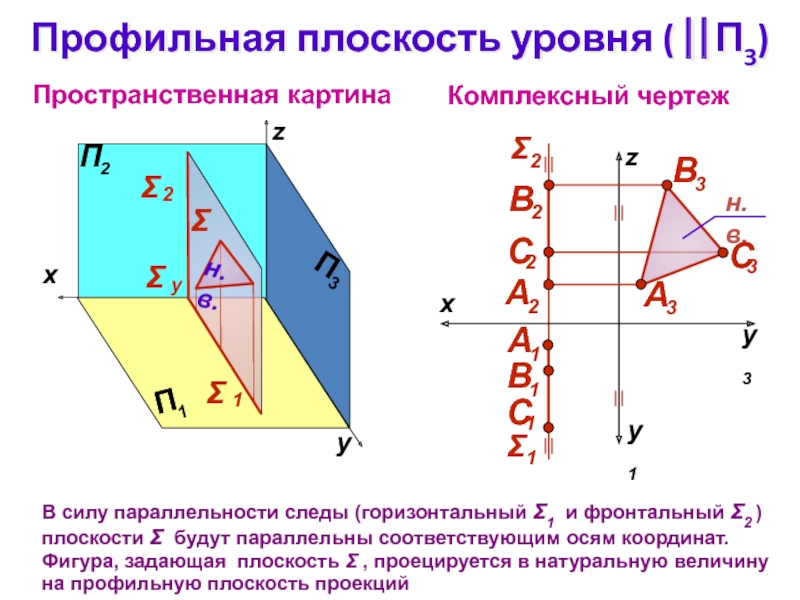
соответствующим осям координат. Фигура, задающая плоскость , изображается в натуральную величину на фронтальной плоскости проекцийСлайд 15Профильная плоскость уровня ( П3)
Комплексный чертеж
z
Пространственная картина
В силу параллельности следы
(горизонтальный 1 и фронтальный 2 ) плоскости будут параллельны
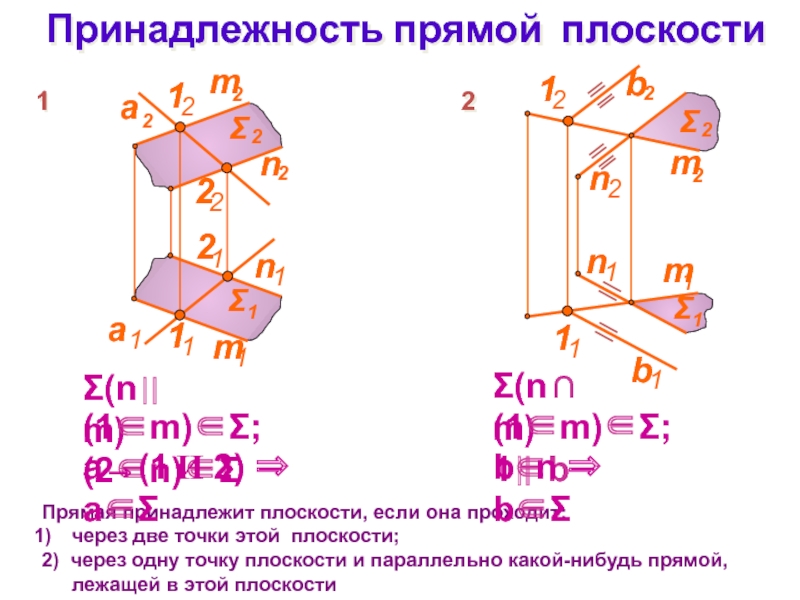
соответствующим осям координат. Фигура, задающая плоскость , проецируется в натуральную величину на профильную плоскость проекцийСлайд 16Принадлежность прямой плоскости
Прямая принадлежит плоскости, если она проходит:
через две
точки этой плоскости;
2) через одну точку плоскости и параллельно
какой-нибудь прямой, лежащей в этой плоскости(n m)
1
(1m); (2n)
а(1 И 2) а
2
(n m)
(1m); 1b
b n b
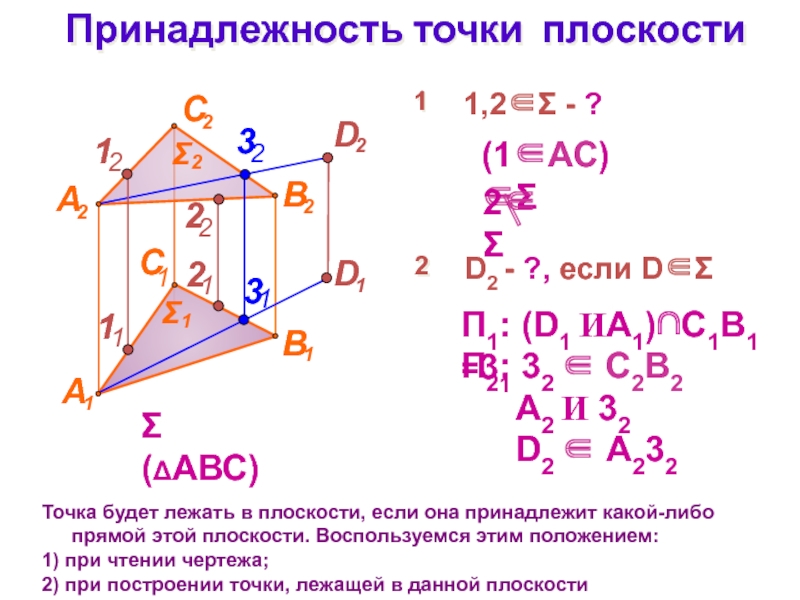
Слайд 17Принадлежность точки плоскости
Точка будет лежать в плоскости, если она принадлежит
какой-либо прямой этой плоскости. Воспользуемся этим положением:
1) при чтении чертежа;
2)
при построении точки, лежащей в данной плоскости(1АС)
П1: (D1 ИA1)С1В1 =31
(АВС)
1
П2: 32 C2B2
1,2 - ?
А2 И 32
D2 А232
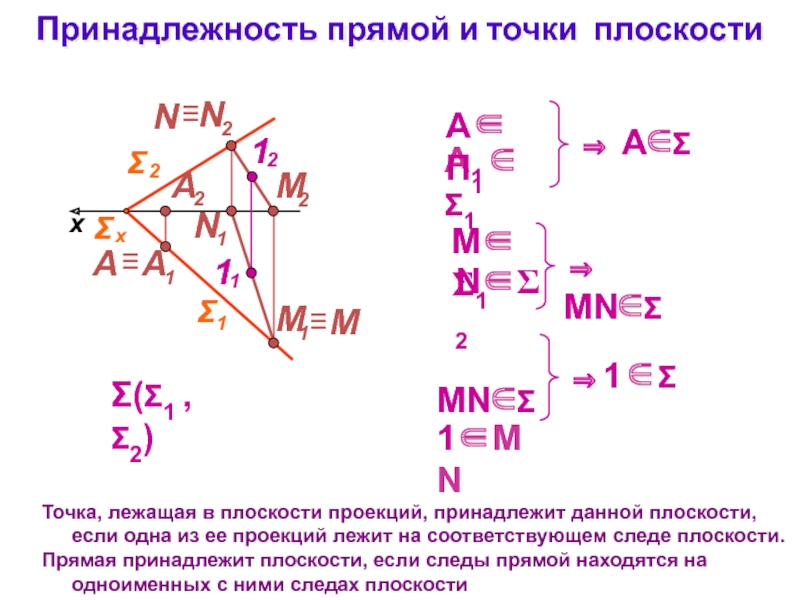
Слайд 18Принадлежность прямой и точки плоскости
(1 , 2)
x
A1 1
АП1
M1
N2
1MN
MN
Точка, лежащая в плоскости проекций, принадлежит данной
плоскости, если одна из ее проекций лежит на соответствующем следе плоскости.Прямая принадлежит плоскости, если следы прямой находятся на одноименных с ними следах плоскости
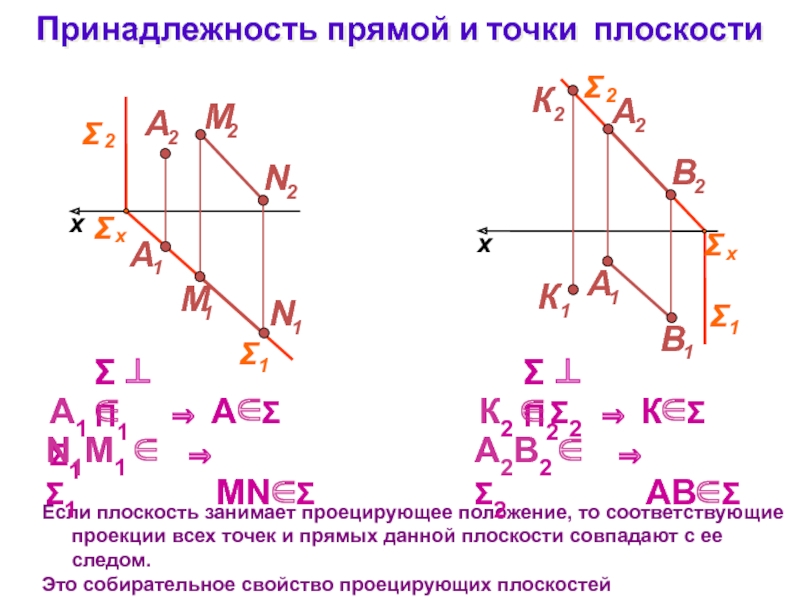
Слайд 19Принадлежность прямой и точки плоскости
Если плоскость занимает проецирующее положение, то
соответствующие проекции всех точек и прямых данной плоскости совпадают с
ее следом.Это собирательное свойство проецирующих плоскостей
П1
x
П2
x
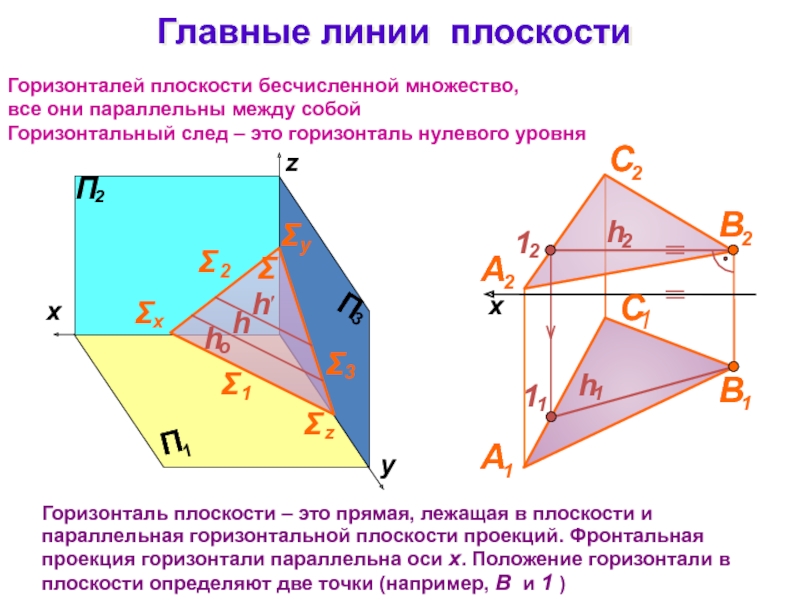
Слайд 20Главные линии плоскости
Горизонталь плоскости – это прямая, лежащая в плоскости
и параллельная горизонтальной плоскости проекций. Фронтальная проекция горизонтали параллельна оси
x. Положение горизонтали в плоскости определяют две точки (например, В и 1 )
Горизонталей плоскости бесчисленной множество,
все они параллельны между собой
Горизонтальный след – это горизонталь нулевого уровня
x
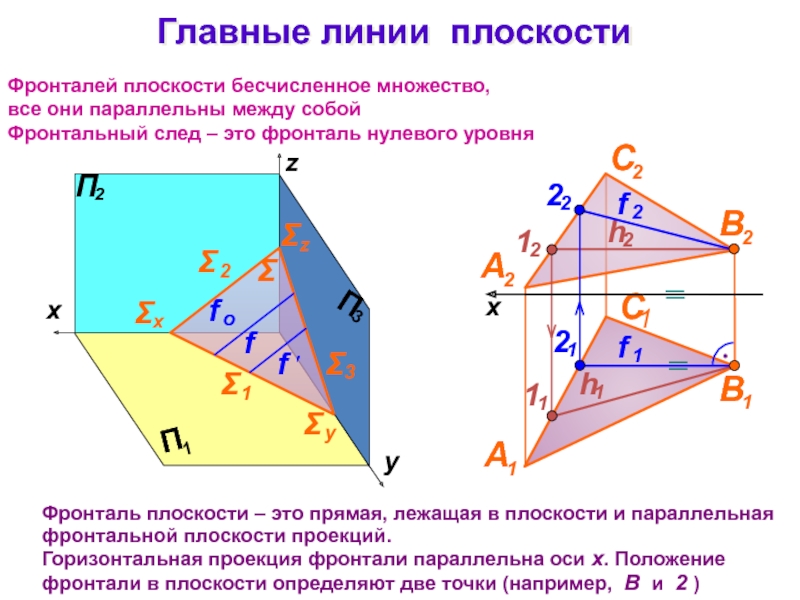
Слайд 21Главные линии плоскости
Фронталей плоскости бесчисленное множество,
все они параллельны между собой
Фронтальный
след – это фронталь нулевого уровня
Фронталь плоскости – это прямая,
лежащая в плоскости и параллельная фронтальной плоскости проекций.Горизонтальная проекция фронтали параллельна оси x. Положение фронтали в плоскости определяют две точки (например, В и 2 )
x
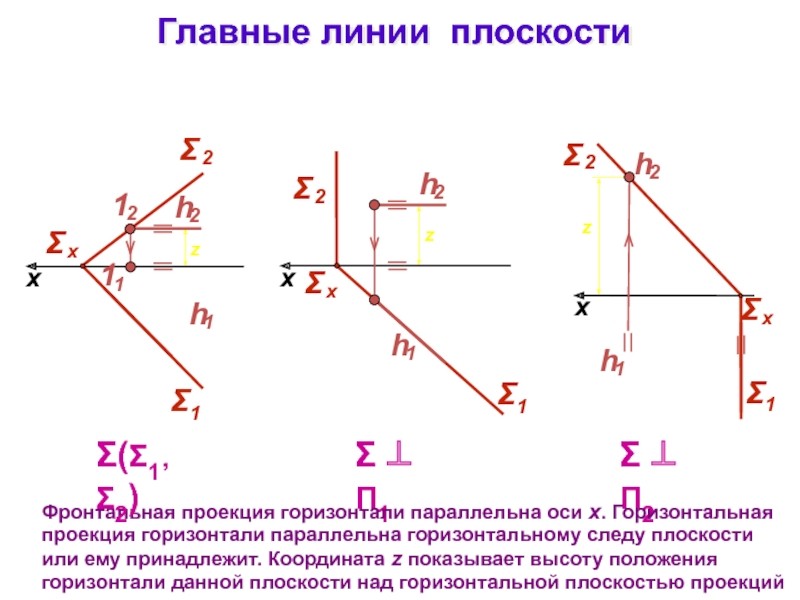
Слайд 22Главные линии плоскости
x
П1
x
П2
x
Фронтальная проекция горизонтали параллельна
оси x. Горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости или
ему принадлежит. Координата z показывает высоту положения горизонтали данной плоскости над горизонтальной плоскостью проекций(1 ,2)
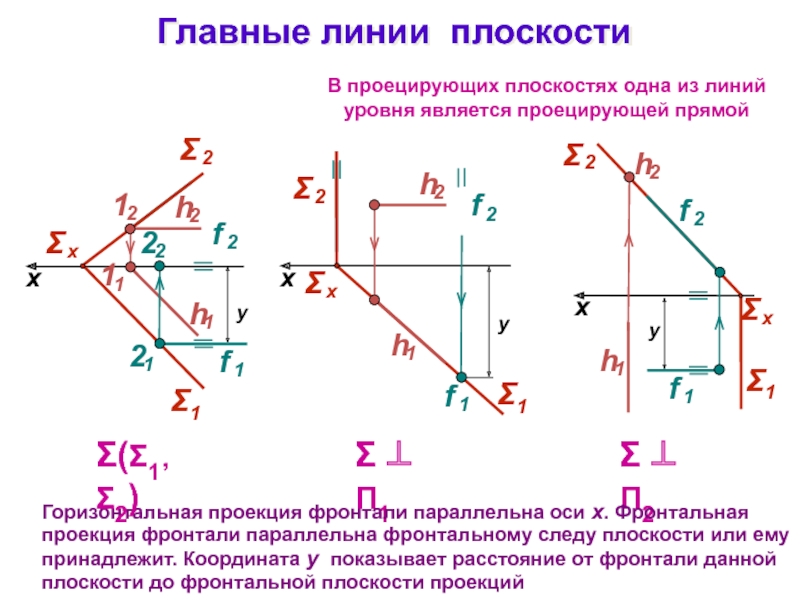
Слайд 23Главные линии плоскости
x
П1
x
П2
x
В проецирующих плоскостях одна
из линий уровня является проецирующей прямой
Горизонтальная проекция фронтали параллельна оси
x. Фронтальная проекция фронтали параллельна фронтальному следу плоскости или ему принадлежит. Координата y показывает расстояние от фронтали данной плоскости до фронтальной плоскости проекций(1 ,2)
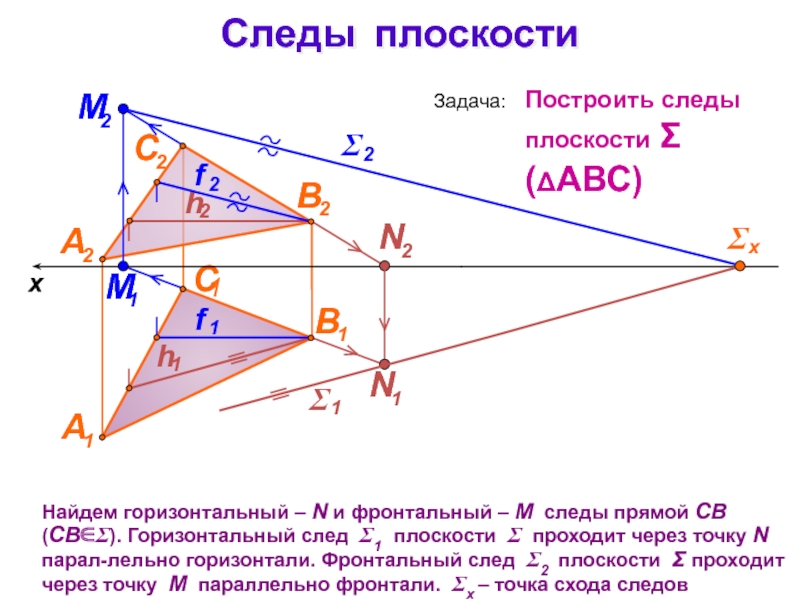
Слайд 24Следы плоскости
Найдем горизонтальный – N и фронтальный – М следы
прямой СВ (СВ). Горизонтальный след 1 плоскости проходит через
точку N парал-лельно горизонтали. Фронтальный след 2 плоскости проходит через точку M параллельно фронтали. x – точка схода следовx
Задача:
Построить следы
плоскости (АВС)
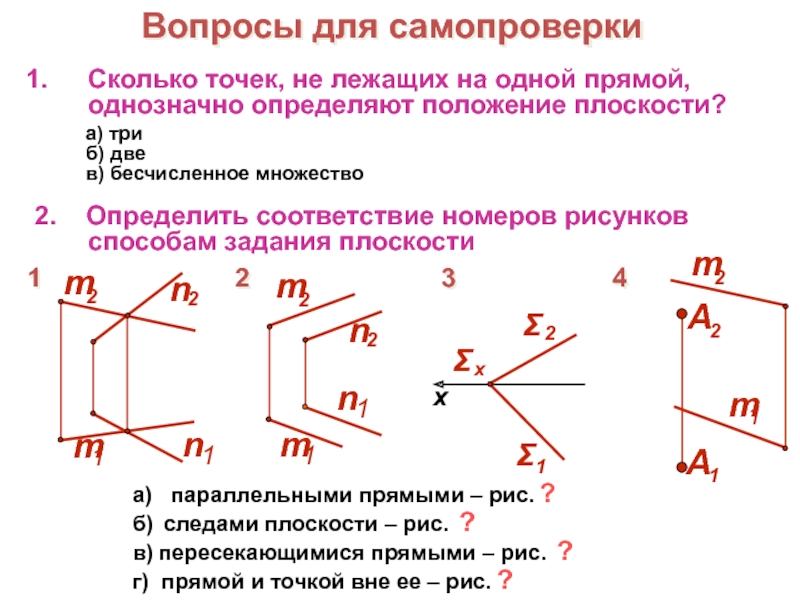
Слайд 25Сколько точек, не лежащих на одной прямой, однозначно определяют положение
плоскости?
а) три
б) две
в) бесчисленное множество
а) параллельными прямыми – рис. ?
б) следами плоскости – рис. ?
в) пересекающимися прямыми – рис. ?
г) прямой и точкой вне ее – рис. ?
Вопросы для самопроверки
Слайд 263. Какая проекция плоскости общего положения изображается в натуральную
величину?
а) фронтальная
б) везде искажается
в) профильная
4. Если плоскость перпендикулярна плоскости проекций, то она проецируется на эту плоскость в виде…
а) следа
б) двух параллельных прямых
в) окружности
5. Если плоскость параллельна плоскости проекций, то ее проекция на эту плоскость есть …
а) натуральная величина плоской фигуры
б) прямая
6. Какие плоскости обладают собирательным свойством?
а) общего положения
б) проецирующие
в) плоскости проекций
Вопросы для самопроверки
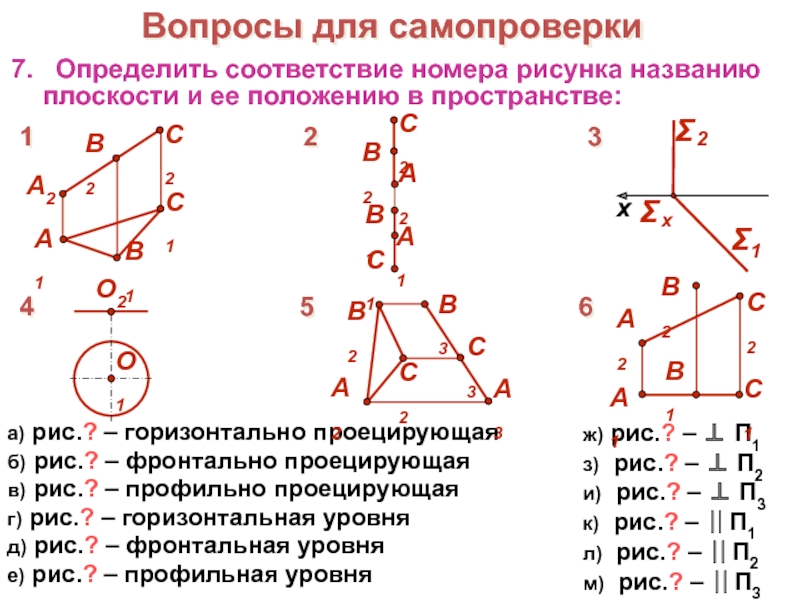
Слайд 27а) рис.? – горизонтально проецирующая
б) рис.? – фронтально проецирующая
в) рис.? – профильно проецирующая
г) рис.? – горизонтальная уровня
д)
рис.? – фронтальная уровняе) рис.? – профильная уровня
ж) рис.? – П1
з) рис.? – П2
и) рис.? – П3
к) рис.? – П1
л) рис.? – П2
м) рис.? – П3
7. Определить соответствие номера рисунка названию плоскости и ее положению в пространстве:
Вопросы для самопроверки
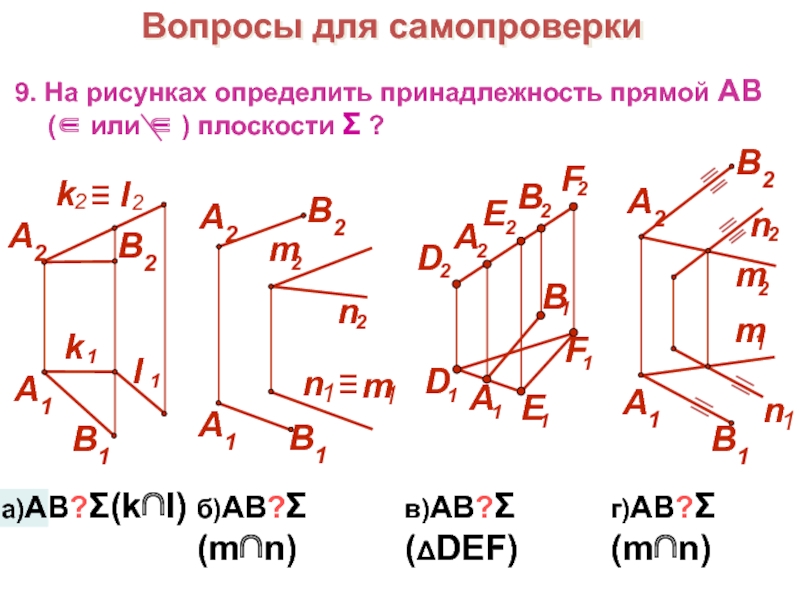
Слайд 30Вопросы для самопроверки
10. Как можно назвать горизонтальный след плоскости?
а) прямая общего положения
б) горизонталь нулевого уровня
в)
проецирующая прямая 11. Как на чертеже проходит фронтальный след плоскости общего положения?
а) параллельно фронтальной проекции фронтали плоскости
б) перпендикулярно оси x
в) параллельно горизонтальному следу плоскости
12. Горизонталь, принадлежащая фронтально проецирующей плоскости занимает положение…
а) фронтально проецирующее
б) общее
в) горизонтально проецирующее
13. Можно ли в плоскости общего положения провести проецирующую прямую?
а) да
б) нет