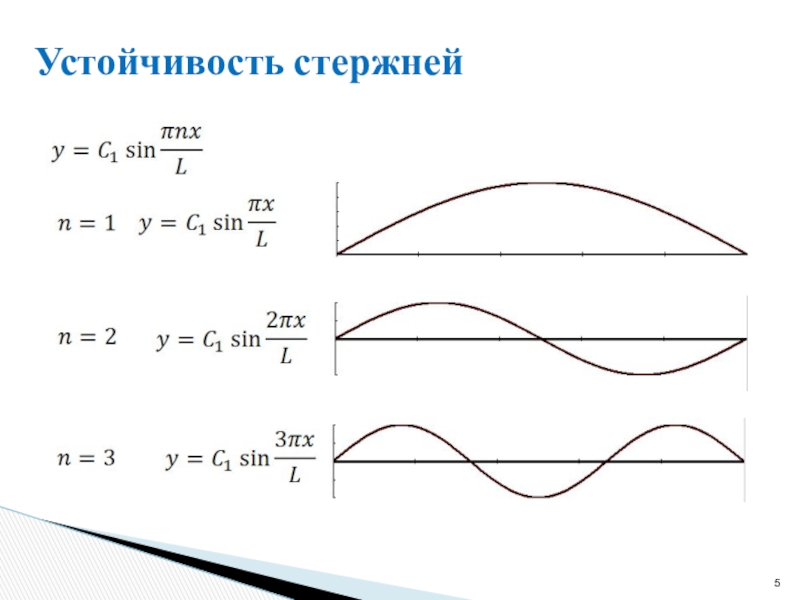
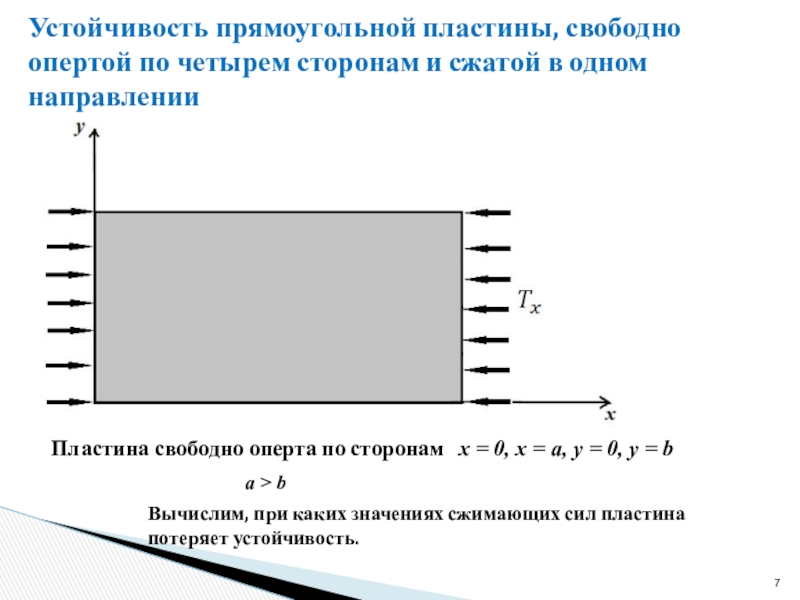
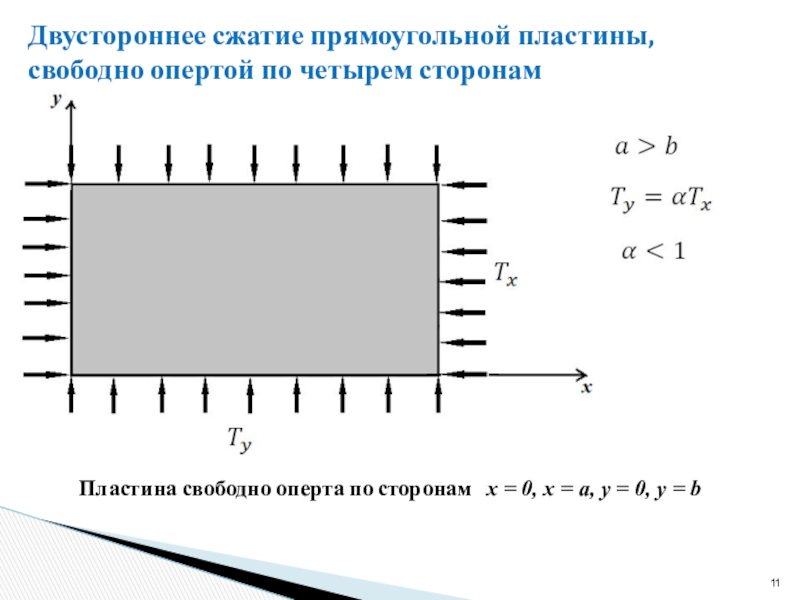
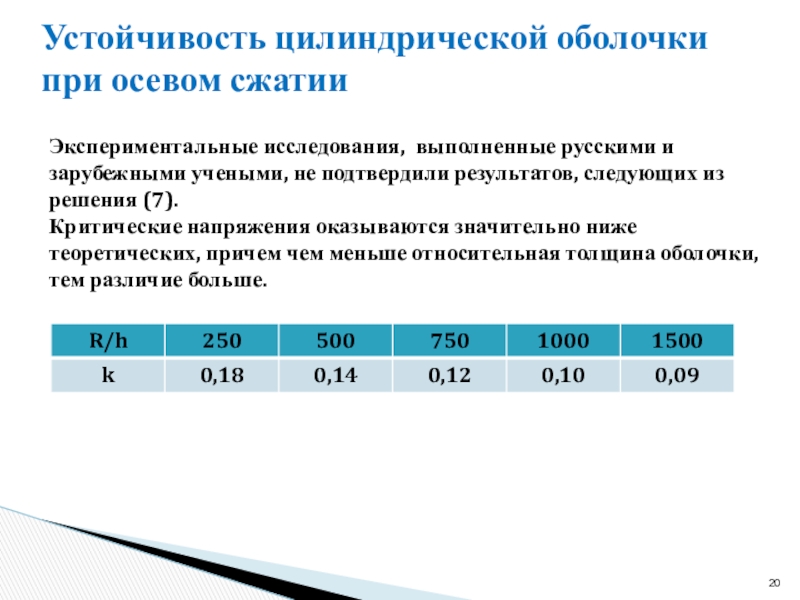
сжатого центральными силами
Под устойчивостью понимается свойство системы самостоятельно восстанавливать свое
первоначальное состояние после того, как ей было сообщено некоторое отклонение от положения равновесия.При малых прогибах
Изгиб стержня происходит в плоскости минимальной жесткости и поэтому под величиной I понимается минимальный момент инерции сечения.