Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕМА 7. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Содержание
- 1. ТЕМА 7. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
- 2. ПервоÓбразная: Задача дифференциального исчисления (предыдущая тема):
- 3. Пример:
- 4. Для всякой ли функции f(x) существует первообразная?
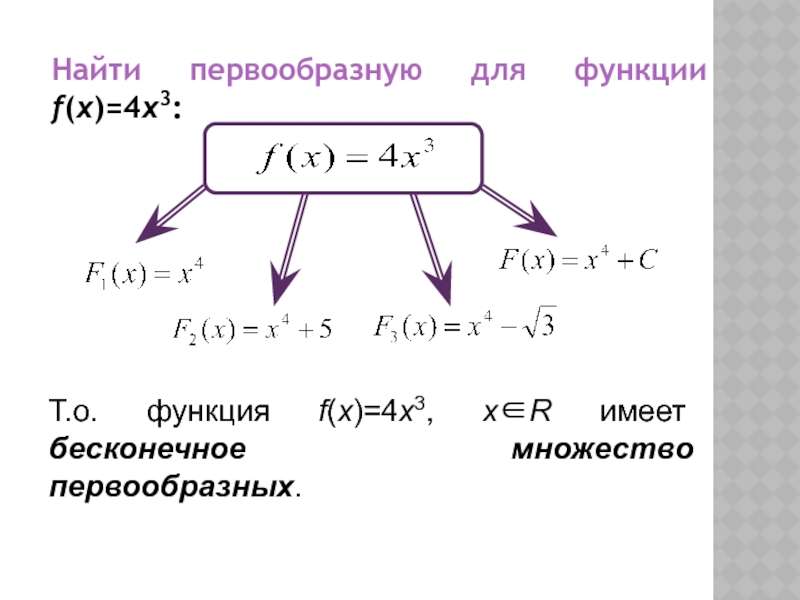
- 5. Найти первообразную для функции f(x)=4x3:Т.о. функция f(x)=4x3, х∈R имеет бесконечное множество первообразных.
- 6. Теорема. Если функция F(x) является первообразной для функции
- 7. Пример: Найти все первообразные функции f(x) = 2x
- 8. Неопределённый интеграл: Множество всех первообразных F(x)+C функции f(x)
- 9. Слайд 9
- 10. Свойства неопределённого интеграла10. Дифференциал от неопределённого интеграла
- 11. Доказательство: То есть правильность интегрирования проверяется дифференцированием.Равенство:верно, так как
- 12. 20. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е.:Доказательство:
- 13. 30. Неопределённый интеграл от алгебраической суммы (разности)
- 14. 40. Постоянный множитель можно выносить за знак интеграла, т.е
- 15. Таблица неопределенных интегралов Пользуясь тем, что интегрирование –
- 16. Таблица неопределенных интегралов (для замены переменной х на u)
- 17. Таблица неопределенных интегралов
- 18. Таблица неопределенных интегралов
- 19. Основные методы интегрированияМетод непосредственного интегрированияНепосредственным интегрированием называется
- 20. Метод интегрирования подстановкойМетод интегрирования подстановкой заключается
- 21. Метод интегрирования по частям
- 22. Теоремы
- 23. Интегрирование рациональных выражений
- 24. Пример 1. Вычислить интеграл
- 25. Пример 2. Вычислить интеграл
- 26. Пример 3. Вычислить интеграл
- 27. Пример 4. Вычислить интеграл
- 28. Пример 5. Вычислить интеграл
- 29. Пример 6. Вычислить интеграл
- 30. Пример 7. Вычислить интеграл
- 31. Пример 8. Вычислить интеграл
- 32. Пример 9. Вычислить интеграл
- 33. Пример 10. Вычислить интеграл
- 34. Скачать презентанцию
ПервоÓбразная: Задача дифференциального исчисления (предыдущая тема): по данной функции найти её производную. Задача интегрального исчисления: найти функцию, зная её производную.Функция F(x) называется первообразной для функции f(x) на заданном промежутке, если для
Слайды и текст этой презентации
Слайд 2 ПервоÓбразная:
Задача дифференциального исчисления (предыдущая тема): по данной функции
найти её производную.
F(x) называется первообразной для функции f(x) на заданном промежутке, если для любого х из этого промежутка справедливо равенство Fʹ(x) = f(x)Слайд 4 Для всякой ли функции f(x) существует первообразная?
Теорема. Если функция
непрерывна на каком- нибудь промежутке, то она имеет на нём первообразную.
Слайд 5Найти первообразную для функции f(x)=4x3:
Т.о. функция f(x)=4x3, х∈R имеет бесконечное
множество первообразных.
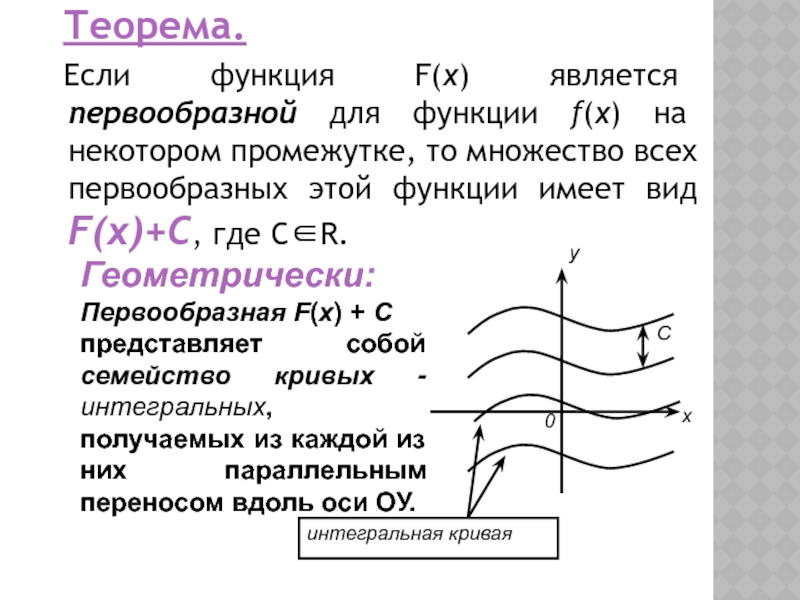
Слайд 6 Теорема.
Если функция F(x) является первообразной для функции f(x) на некотором
промежутке, то множество всех первообразных этой функции имеет вид F(x)+C,
где C∈R.Слайд 7Пример:
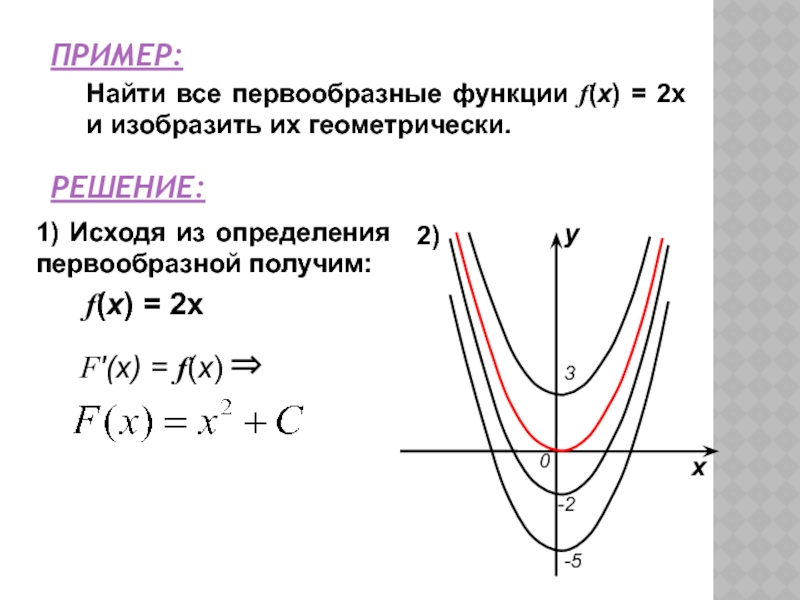
Найти все первообразные функции f(x) = 2x и изобразить их
геометрически.
решение:
1) Исходя из определения первообразной получим:
2)
f(x) =
2xFʹ(x) = f(x)
Слайд 8Неопределённый интеграл:
Множество всех первообразных F(x)+C функции f(x) на некотором промежутке
называется неопределённым интегралом и обозначается символом
, т.еСлайд 10Свойства неопределённого интеграла
10. Дифференциал от неопределённого интеграла равен подынтегральному выражению,
а производная неопределённого интеграла равна подынтегральной функции:
Слайд 11 Доказательство:
То есть правильность интегрирования проверяется дифференцированием.
Равенство:
верно, так как
Слайд 1220. Неопределённый интеграл от дифференциала некоторой функции равен этой функции
плюс произвольная постоянная, т.е.:
Доказательство:
Слайд 1330. Неопределённый интеграл от алгебраической суммы (разности) двух или нескольких
функций равен алгебраической суммы (разности) их интегралов, т.е.:
Доказательство: воспользуемся свойством 10.
Слайд 15Таблица неопределенных интегралов
Пользуясь тем, что интегрирование – процесс обратный дифференцированию,
можно получить таблицу основных интегралов путем обращения формул дифференцирования и
использования свойств неопределенного интегралаОтметим, что в таблице основных интегралов переменная интегрирования u может обозначать как независимую переменную, так и функцию от независимой переменой.
Слайд 19Основные методы интегрирования
Метод непосредственного интегрирования
Непосредственным интегрированием называется такой метод вычисления
интегралов, при котором они сводятся к табличным путём применения к
ним основных свойств неопределённого интеграла. При этом подынтегральную функцию обычно соответствующим образом преобразуют.Слайд 20 Метод интегрирования подстановкой
Метод интегрирования подстановкой заключается во введении новой
переменной интегрирования (т.е. подстановки ). При этом заданный интеграл приводится
к новому интегралу, который является табличным или к нему сводящимся (в случае удачной подстановки)Пусть требуется вычислить интеграл Сделаем подстановку где
функция имеющая непрерывную производную тогда
На основании инвариантности формулы интегрирования неопределенного интеграла получим формулу интегрирования подстановкой
Эта формула называется формулой интегрирования заменой переменой в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t к переменой x