Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 8. Многогранники. Тела вращения
Содержание
- 1. Тема 8. Многогранники. Тела вращения
- 2. ОпределениеМногогранником называется поверхность, которая составлена из многоугольников и ограничивает некоторое геометрическое телограньреброBвершинадиагональ гранидиагональ многогранника
- 3. Многогранник - геометрическое тело,
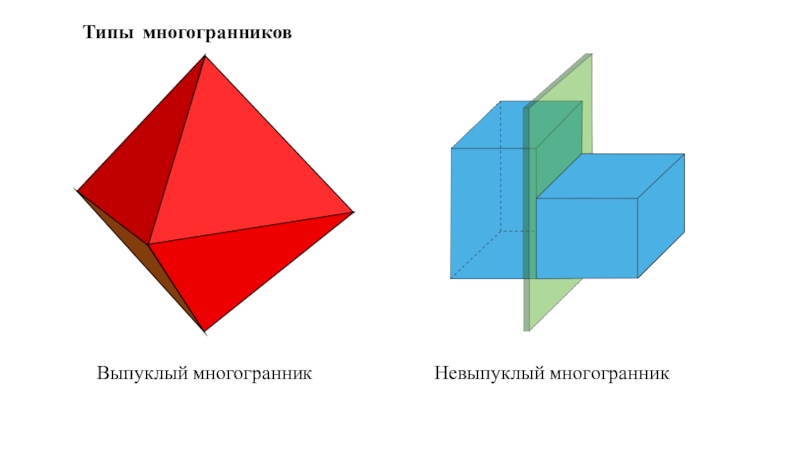
- 4. Выпуклый многогранникНевыпуклый многогранник Типы многогранников
- 5. φ1φ2φ3φ3φ2φ1φ1 + φ2 + φ3 < 360°
- 6. 90° + 90° + 90° = 270°
- 7. ТетраэдрКубОктаэдрДодекаэдрИкосаэдрМногогранник называется правильным, если его грани правильные
- 8. Слайд 8
- 9. Правильный икосаэдрсоставлен из двадцати равносторонних треугольников. Каждая
- 10. Правильный додекаэдрсоставлен из двенадцати правильных пятиугольников. Каждая
- 11. Правильный октаэдрсоставлен из восьми равносторонних треугольников. Каждая
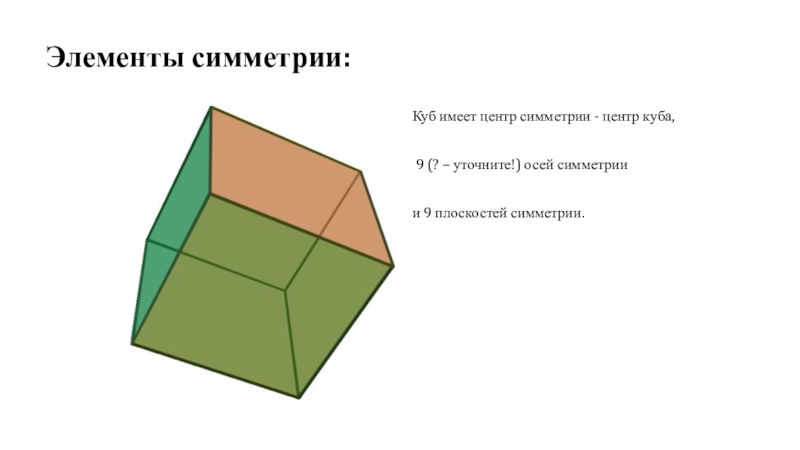
- 12. Элементы симметрии: Куб имеет центр симметрии -
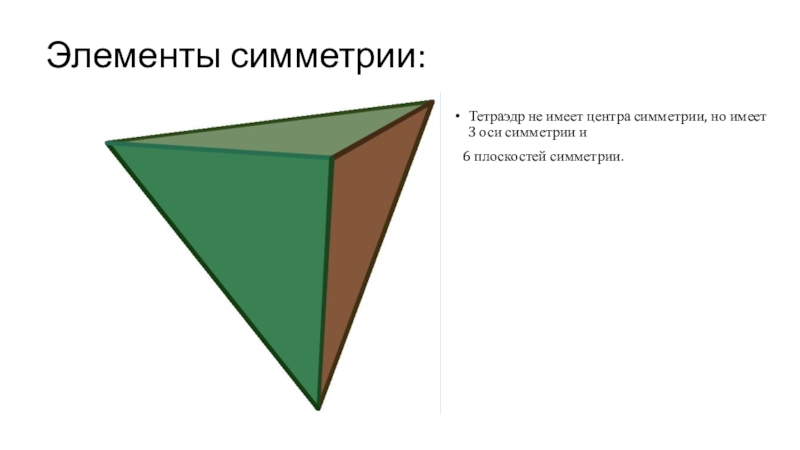
- 13. Элементы симметрии: Тетраэдр не имеет центра симметрии,
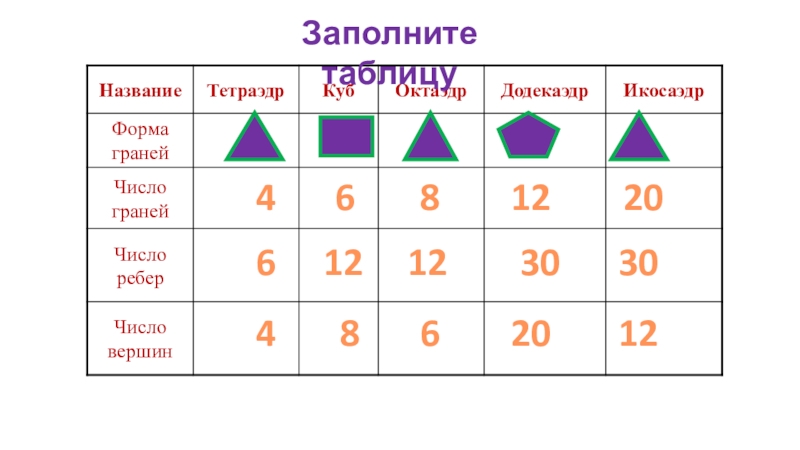
- 14. Заполните таблицу44666881212121220203030
- 15. Прямой параллелепипед – это параллелепипед, у которого боковые грани являются прямоугольниками.АВСDA1B1С1D1abc
- 16. Прямоугольный параллелепипед– это параллелепипед, у которого все
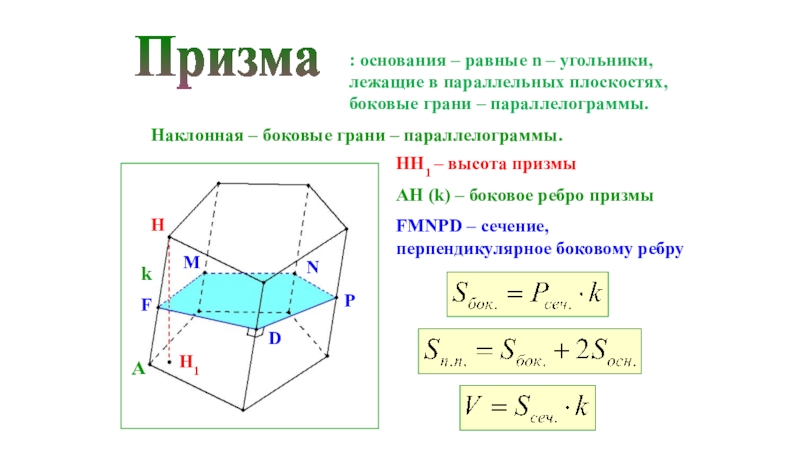
- 17. Призма: основания – равные n – угольники,
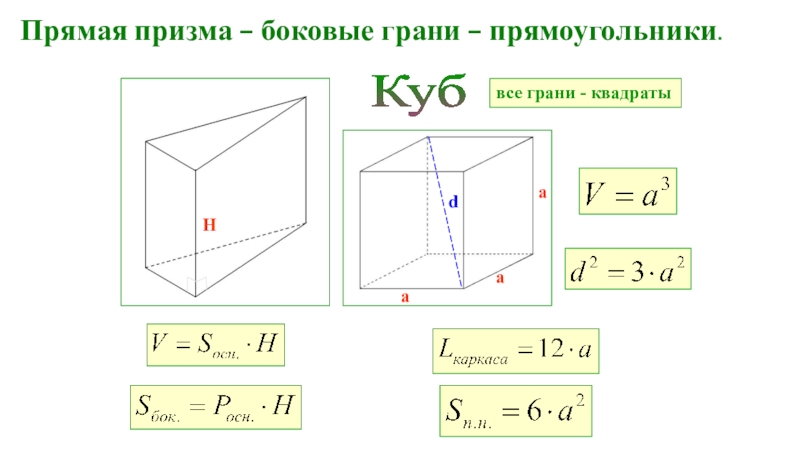
- 18. Прямая призма – боковые грани – прямоугольники. Кубаааdвсе грани - квадратыH
- 19. Пирамида– это многогранник, состоящий из n-угольника А1А2А3...Аn
- 20. Правильная пирамида основание – правильный многоугольник, вершина
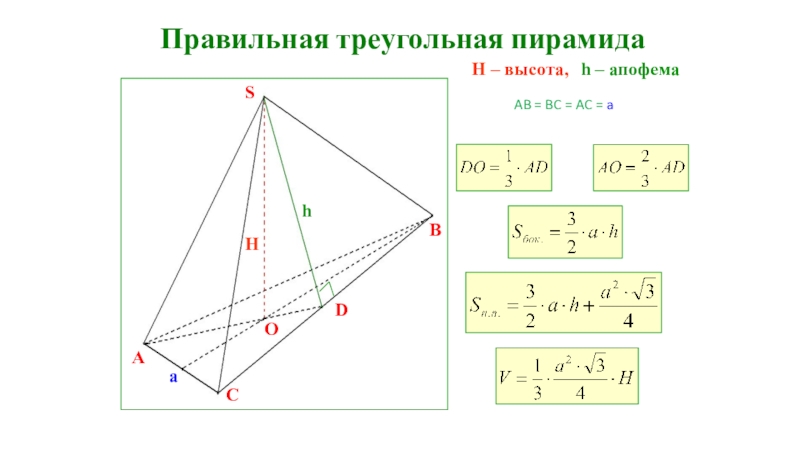
- 21. AB = BC = AC = aПравильная треугольная пирамидаH – высота, h – апофема AOBChHSDa
- 22. Правильная четырехугольная пирамидаh – апофема, H –
- 23. PA1A2…An – произвольная пирамидаα – плоскость основанияβ
- 24. Задача 1АВСDА1В1С1D1 — прямоугольный параллелепипедДано:АС1^(АВС) = 45°Найти:
- 25. Решение:1. Отрезок СС1 перпендикулярен плоскости (АВС), а
- 26. Задача 2АВСDА1В1С1D1 — прямой параллелепипедДано:АС = 24
- 27. Решение:1.В ромбе АВСD большей диагональю является АС,
- 28. Задача 3АВСА1В1С1 — прямая треугольная призмаДано:∠ВА1С =
- 29. Прежде чем приступить к решению задачи необходимо
- 30. Слайд 30
- 31. Многогранники в искусствеВ эпоху Возрождения большой интерес
- 32. Наука геометрия возникла из практических задач, ее
- 33. Великая пирамида была построена как гробница
- 34. Слайд 34
- 35. ТРИ БАШНИФаросский маяк состоял из трех мраморных
- 36. В III веке до н.э. был
- 37. Кристаллы белого фосфора образованы молекулами Р4 . Такая
- 38. Куб передает форму кристаллов поваренной соли NaCl.
- 39. Форму октаэдра имеет монокристалл алюмокалиевых
- 40. Вирус полиомиелита имеет форму додекаэдра. Он может
- 41. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема 8.
Многогранники.
Тела вращения
Часть 1 . Многогранники
https://infourok.ru/videouroki/1433
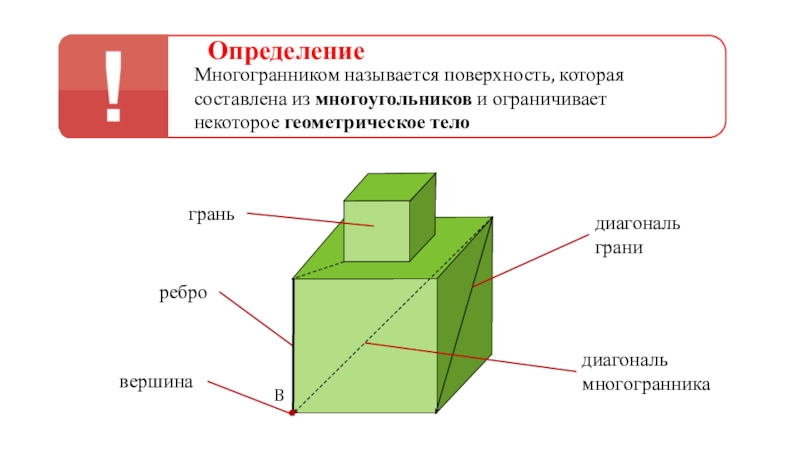
Слайд 2Определение
Многогранником называется поверхность, которая составлена из многоугольников и ограничивает некоторое
геометрическое тело
Слайд 3 Многогранник - геометрическое тело,
ограниченное со всех сторон плоскими
многоугольниками,
называемыми гранями. Стороны граней называются ребрами
многогранника, а концы ребер — вершинами
многогранника. По числу граней различают
четырехгранники, пятигранники и т. д.
Слайд 5φ1
φ2
φ3
φ3
φ2
φ1
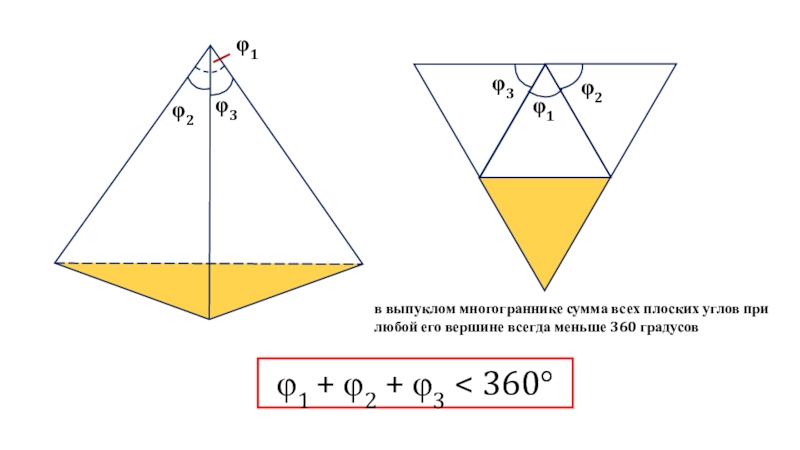
φ1 + φ2 + φ3 < 360°
в выпуклом многограннике
сумма всех плоских углов при любой его вершине всегда меньше
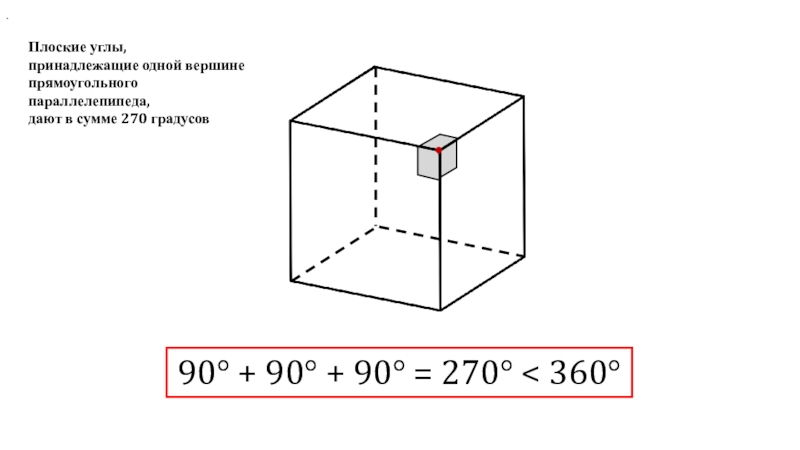
360 градусовСлайд 690° + 90° + 90° = 270° < 360°
.
Плоские углы,
принадлежащие одной вершине прямоугольного параллелепипеда,
дают в сумме 270 градусов
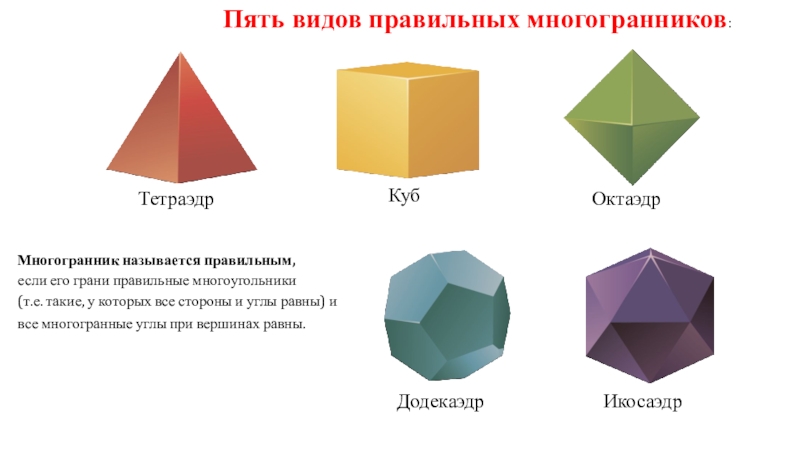
Слайд 7Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
Многогранник называется правильным,
если его грани правильные многоугольники
(т.е. такие,
у которых все стороны и углы равны) и все многогранные
углы при вершинах равны.Пять видов правильных многогранников:
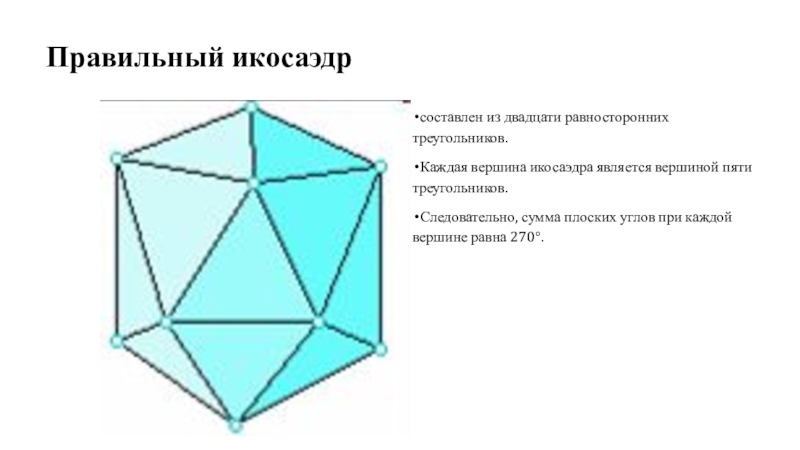
Слайд 9Правильный икосаэдр
составлен из двадцати равносторонних треугольников.
Каждая вершина икосаэдра является
вершиной пяти треугольников.
Следовательно, сумма плоских углов при каждой вершине
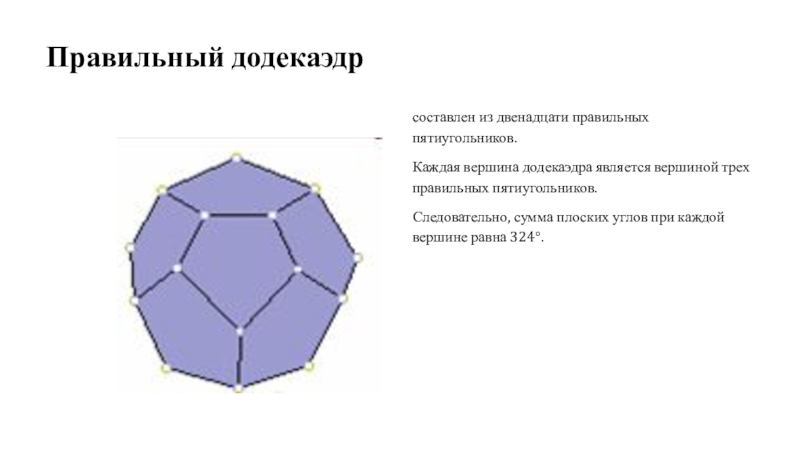
равна 270°.Слайд 10Правильный додекаэдр
составлен из двенадцати правильных пятиугольников.
Каждая вершина додекаэдра является
вершиной трех правильных пятиугольников.
Следовательно, сумма плоских углов при каждой
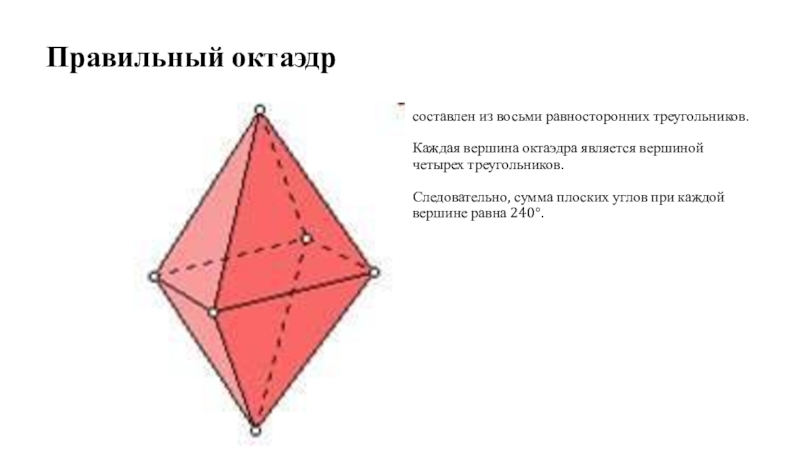
вершине равна 324°.Слайд 11Правильный октаэдр
составлен из восьми равносторонних треугольников.
Каждая вершина октаэдра является
вершиной четырех треугольников.
Следовательно, сумма плоских углов при каждой вершине
равна 240°.Слайд 12Элементы симметрии:
Куб имеет центр симметрии - центр куба,
9
(? – уточните!) осей симметрии
и 9 плоскостей симметрии.
Слайд 13Элементы симметрии:
Тетраэдр не имеет центра симметрии, но имеет 3
оси симметрии и
6 плоскостей симметрии.
Слайд 15Прямой параллелепипед
– это параллелепипед, у которого боковые грани являются
прямоугольниками.
А
В
С
D
A1
B1
С1
D1
a
b
c
Слайд 16Прямоугольный параллелепипед
– это параллелепипед, у которого все грани прямоугольники.
а
b
c
a –
длина, b – ширина,
с – высота, d – диагональ
d
d2
= a2 + b2 + c2Слайд 17Призма
: основания – равные n – угольники, лежащие в параллельных
плоскостях, боковые грани – параллелограммы.
Наклонная – боковые грани –
параллелограммы.H
H1
A
k
F
M
N
P
D
HH1 – высота призмы
AH (k) – боковое ребро призмы
FMNPD – сечение, перпендикулярное боковому ребру
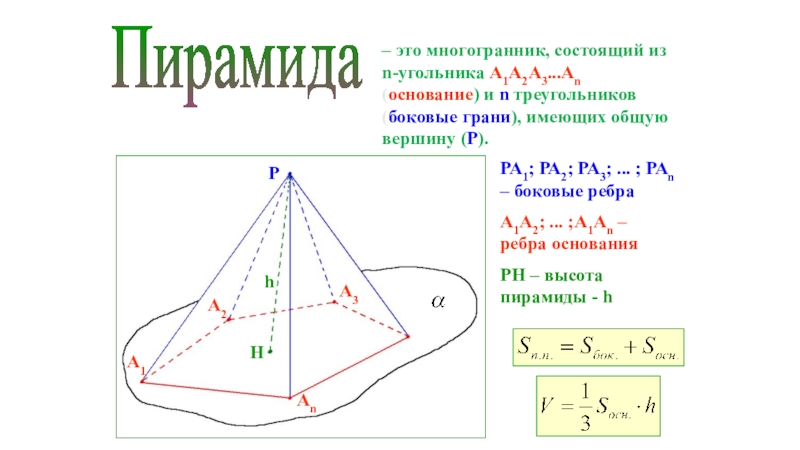
Слайд 19Пирамида
– это многогранник, состоящий из n-угольника А1А2А3...Аn (основание) и n
треугольников (боковые грани), имеющих общую вершину (Р).
Р
А1
А2
А3
Аn
H
РА1; РА2; РА3;
... ; РАn – боковые ребраА1А2; ... ;А1Аn – ребра основания
РH – высота пирамиды - h
h
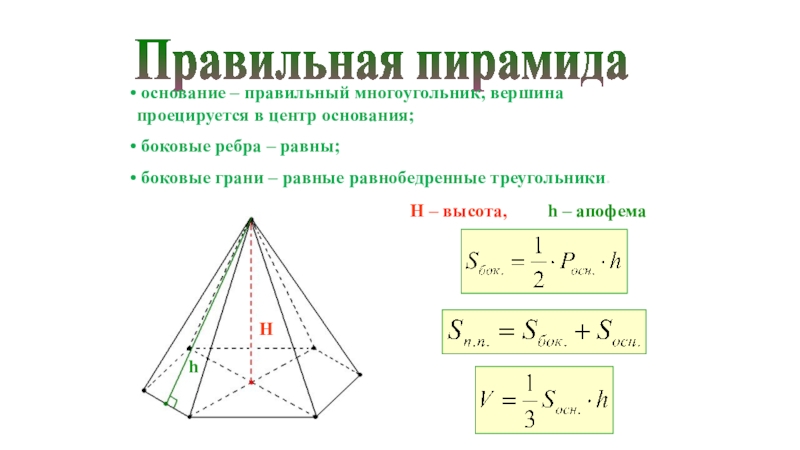
Слайд 20Правильная пирамида
основание – правильный многоугольник, вершина проецируется в центр
основания;
боковые ребра – равны;
боковые грани – равные равнобедренные
треугольники. H – высота,
h – апофема
H
h
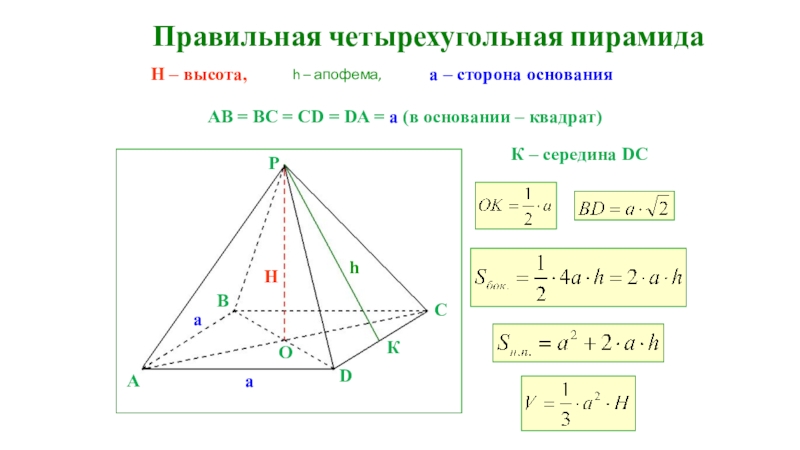
Слайд 22Правильная четырехугольная пирамида
h – апофема,
H – высота,
AB =
BC = CD = DA = a (в основании –
квадрат)H
h
a
a
A
B
D
O
P
К
К – середина DC
C
а – сторона основания
Слайд 23PA1A2…An – произвольная пирамида
α – плоскость основания
β – секущая плоскость,
PB1B2…Bn – пирамида
Усеченная пирамида
β
α
P
A1
A2
A3
An
B1
B3
Bn
B2
O
O1
H
B1B2…Bn – верхнее основание
A1A2…An –
нижнее снованиеA1B1B2A2; …; AnBnB1A1 – боковые грани – трапеции
A1B1; A2B2; …; AnBn – боковые ребра
OO1= H – высота
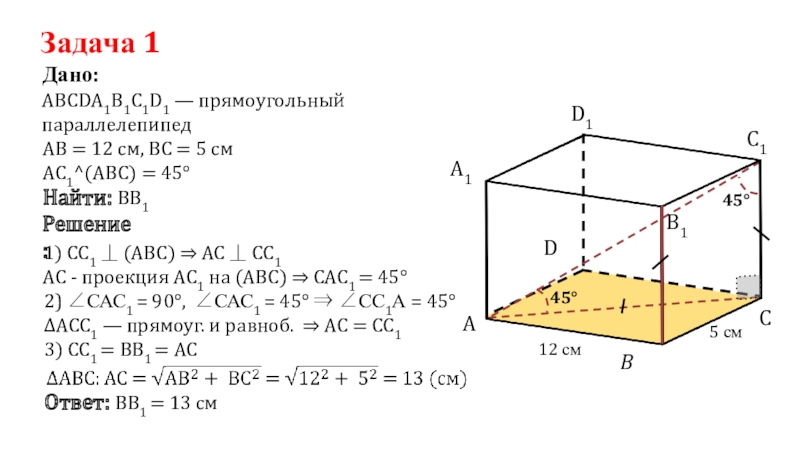
Слайд 24Задача 1
АВСDА1В1С1D1 — прямоугольный параллелепипед
Дано:
АС1^(АВС) = 45°
Найти: ВВ1
1) СС1 ⏊
(АВС) ⇒ АС ⏊ СС1
АС - проекция АС1 на (АВС)
⇒ САС1 = 45°АВ = 12 см, ВС = 5 см
2) ∠САС1 = 90°, ∠САС1 = 45° ⇒ ∠СС1А = 45°
ΔАСС1 — прямоуг. и равноб. ⇒ АС = СС1
3) СС1 = ВВ1 = АС
A
D
C
B
A1
D1
C1
B1
Ответ: ВВ1 = 13 см
12 см
5 см
45°
45°
Решение:
Слайд 25Решение:
1. Отрезок СС1 перпендикулярен плоскости (АВС), а значит отрезок АС
перпендикулярен отрезку СС1, поэтому проекцией АС1 на плоскость (АВС) является
АС. Отсюда следует, что углом между диагональю АС1 и плоскостью (АВС) является угол САС1, который по условию равен 45 градусов.2.Рассмотрим треугольник АСС1: угол САС1 прямой, угол САС1 равен 45 градусов. Известно, что сумма двух острых углов прямоугольного треугольника равна 90 градусов, значит угол СС1А так же равен 45 градусам.
Исходя из этого можно сделать вывод, что треугольник АСС1 прямоугольный и равнобедренный, поэтому отрезок АС равен отрезку СС1
3.В параллелепипеде противоположные рёбра равны, значит искомое ребро ВВ1 равно ребру СС1, которое в свою очередь равно отрезку АС.
Из треугольника АВС по теореме Пифагора найдем АС= = = =13см .
АС=ВВ 1=13 см
Задача 1
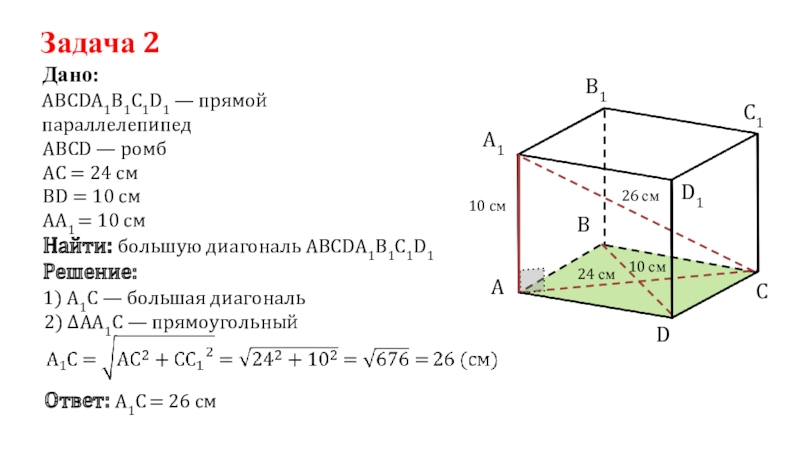
Слайд 26Задача 2
АВСDА1В1С1D1 — прямой параллелепипед
Дано:
АС = 24 см
ВD = 10
см
Найти: большую диагональ АВСDА1В1С1D1
1) А1С — большая диагональ
АВСD — ромб
2)
ΔАА1С — прямоугольный
A
B
C
D
A1
B1
C1
D1
Ответ: А1С = 26 см
АА1 = 10 см
24 см
10 см
10 см
Решение:
26 см
Слайд 27Решение:
1.В ромбе АВСD большей диагональю является АС, которая в свою
очередь является проекцией диагонали А1С параллелепипеда (чем больше проекция, тем
больше её наклонная.), значит диагональ А1С искомая.2. Треугольник АА1С прямоугольный, так как А1 А перпендикулярна плоскости (АСД). По теореме Пифагора найдем А1 С=√АС2+СС12=√242+102=√676=26 см.
Ответ: А1С=26 см
Задача 2
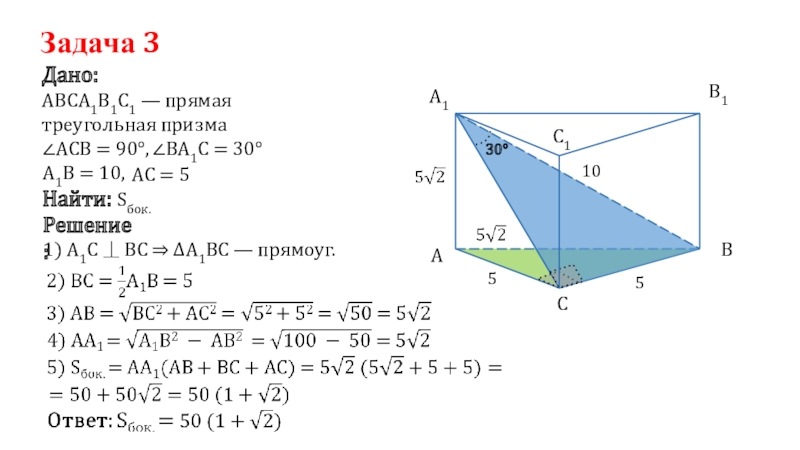
Слайд 28Задача 3
АВСА1В1С1 — прямая треугольная призма
Дано:
∠ВА1С = 30°
А1В = 10,
Решение:
1) А1С ⏊ ВС ⇒ ΔА1ВС — прямоуг.
∠AСB = 90°,
Найти:
Sбок.
A
B
C
A1
B1
C1
30°
АС = 5
10
5
5
Слайд 29Прежде чем приступить к решению задачи необходимо провести её краткий
анализ:
площадь боковой поверхности прямой призмы равна произведению высоты призмы на
периметр её основания,а это стороны: АС, ВС, АВ и высота АА1.Из условия известна длина только отрезка АС, поэтому прежде чем приступить к решению задачи, необходимо определить недостающие данные, а это ВС, АВ и АА1.Решение:
1.По теореме о трёх перпендикулярах отрезок А1С перпендикулярен ВС, таким образом треугольник А1ВС прямоугольный.
2.Известно, что катет лежащий против угла в 30 градусов равен половине гипотенузы, значит катет ВС равен половине гипотенузы А1В, то есть равен 5.
3.Теперь нам известна сторона ВС равная 5, АС равна 5 по условию и мы можем найти АВ по теореме Пифагора из прямоугольного треугольника АВС:
АВ=√ВС2+АС2=√52+52=√50=5√2
4.Из прямоугольного треугольника А1 АВ так же по теореме Пифагора находим АА1:
АА1=√А1В2-АВ2=√100-50=5√2
5.Таким образом, все неизвестные величины найдены и мы можем приступить к нахождению площади боковой поверхности призмы
Sбок=АА1(АВ+ВС+АС)=5√2(5√2+5+5)=50+50√2
Общий множитель 50 можно вынести за скобку
Отсюда Sбок=50(1+√2)
Ответ: Sбок=50(1+√2)
Задача 3
Слайд 31Многогранники в искусстве
В эпоху Возрождения большой интерес к формам правильных
многогранников проявили скульпторы. архитекторы, художники.
Леонардо да Винчи (1452 -1519)
например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал правильными и полуправильными многогранниками книгу
Монаха Луки Пачоли ''О божественной пропорции.''
Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в известной гравюре ''Меланхолия '‘ на переднем плане изобразил додекаэдр.
художник Эшер
Слайд 32Наука геометрия возникла из практических задач, ее предложения выражают реальные
факты и находят многочисленные применения. В конечном счете в основе
всей техники так или иначе лежит геометрия, потому что она появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров. И технику, и инженеру, и квалифицированному рабочему и людям искусства геометрическое воображение необходимо, как геометру или архитектору. Математика, в частности геометрия, представляет собой могущественный инструмент познания природы, создания техники и преобразования мира.Различные геометрические формы находят свое отражение практически во во всех отраслях знаний: архитектура, искусство.
Многогранники в архитектуре
Слайд 33 Великая пирамида была построена как гробница Хуфу, известного грекам
как Хеопс. Он был одним из фараонов, или царей древнего
Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте. ЦАРСКАЯ ГРОБНИЦА
Слайд 35ТРИ БАШНИ
Фаросский маяк состоял из трех мраморных башен, стоявших на
основании из
массивных каменных блоков.
Первая башня была прямоугольной, в
ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню.
Слайд 36 В III веке до н.э. был построен маяк, чтобы
корабли могли благополучно миновать рифы на пути в Александрийскую бухту.
Ночью им помогало в этом отражение языков пламени, а днем - столб дыма.
Это был первый в мире маяк, и простоял он 1500 лет.
Александрийский маяк.
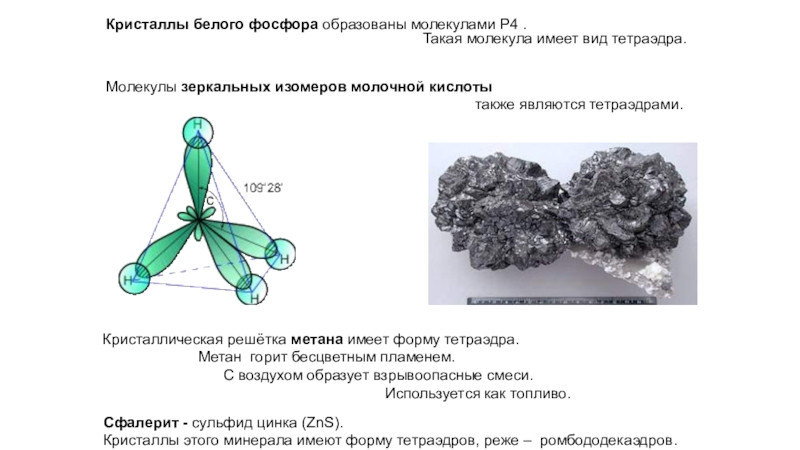
Слайд 37Кристаллы белого фосфора образованы молекулами Р4 .
Такая молекула имеет вид
тетраэдра.
Молекулы зеркальных изомеров молочной кислоты
также являются тетраэдрами. Кристаллическая решётка метана имеет форму тетраэдра.
Метан горит бесцветным пламенем.
С воздухом образует взрывоопасные смеси.
Используется как топливо.
Сфалерит - сульфид цинка (ZnS).
Кристаллы этого минерала имеют форму тетраэдров, реже – ромбододекаэдров.
Слайд 38Куб передает форму кристаллов поваренной соли NaCl.
Форму куба имеют
кристаллические решётки
многих металлов (Li, Na, Cr, Pb,
Al, Au, и другие)Интересно сравнить этот рисунок Леонардо с похожей работой Маурица Эшера,
относящейся к 1952 г., «Ячейки кубического пространства».
Леонардо да Винчи – метод жестких ребер
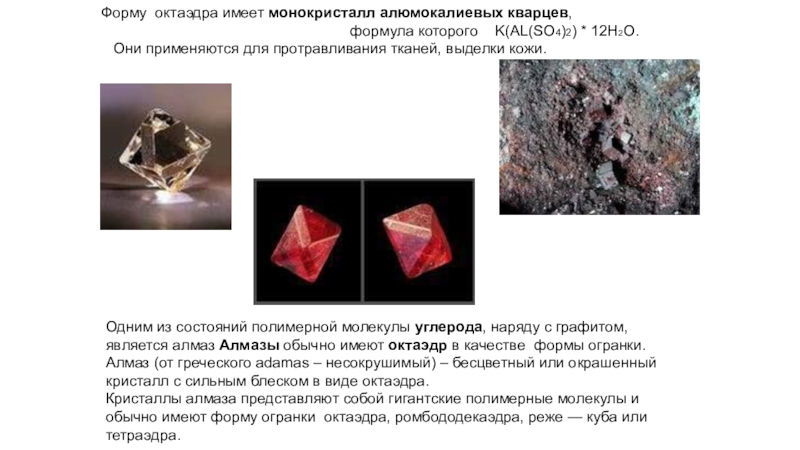
Слайд 39 Форму октаэдра имеет монокристалл алюмокалиевых кварцев,
Они применяются для протравливания тканей, выделки кожи.
Одним из состояний полимерной молекулы углерода, наряду с графитом, является алмаз Алмазы обычно имеют октаэдр в качестве формы огранки.
Алмаз (от греческого adamas – несокрушимый) – бесцветный или окрашенный кристалл с сильным блеском в виде октаэдра.
Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму огранки октаэдра, ромбододекаэдра, реже — куба или тетраэдра.