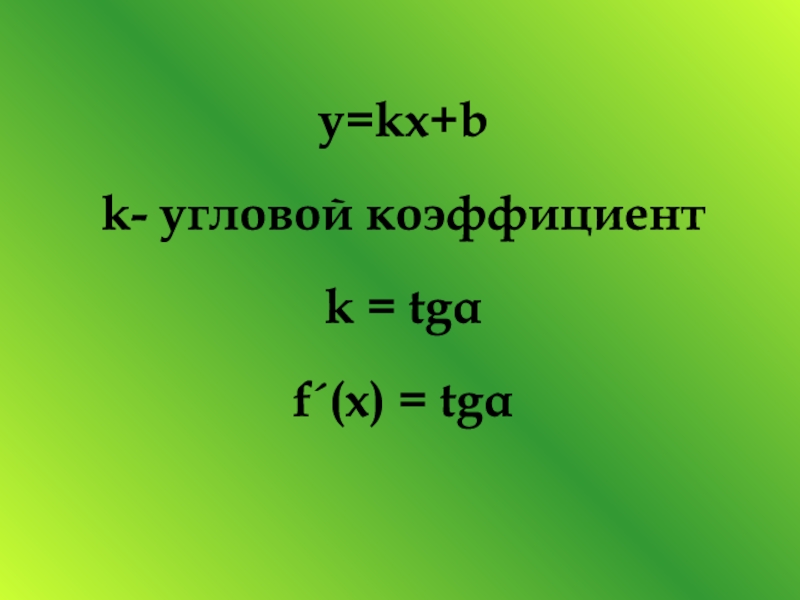Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕМА УРОКА: Касательная. Уравнение касательной
Содержание
- 1. ТЕМА УРОКА: Касательная. Уравнение касательной
- 2. Девиз урока:Плохих идей не бываетМыслите творческиРискуйте Не критикуйте
- 3. Используя формулы и правила дифференцирования, найдите производные следующих функций:
- 4. Согласны ли вы с утверждением:Касательная – это прямая, имеющая с данной кривой одну общую точку
- 5. ЦЕЛИ УРОКА:1. Уточнить понятие касательной к графику
- 6. y=kx+bk- угловой коэффициентk = tgαf´(x) = tgα
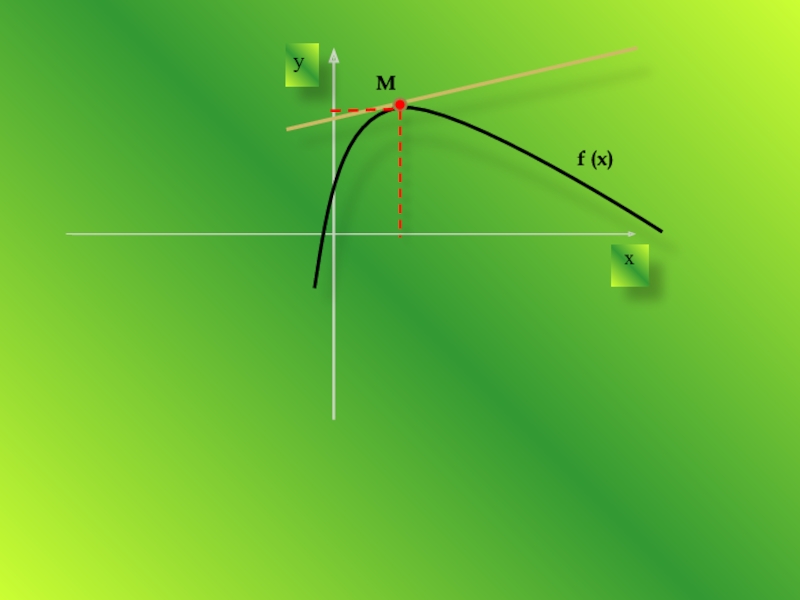
- 7. yxf (x)M
- 8. Уравнение касательнойy = f(a) + f /
- 9. Алгоритм 1. Обозначим абсциссу точки касания буквой
- 10. Потренируемся:Составить уравнение касательной к графику функции f(x)=x²-3x+5 в точке с абсциссой а = -1
- 11. Самостоятельная работа Напишите уравнение касательной к графику
- 12. Подведение итоговЧто называется касательной к графику функции
- 13. тревожно, не уверен в себеспокойно, у меня
- 14. Спасибо за урок!
- 15. Скачать презентанцию
Девиз урока:Плохих идей не бываетМыслите творческиРискуйте Не критикуйте
Слайды и текст этой презентации
Слайд 4Согласны ли вы с утверждением:
Касательная – это прямая, имеющая с
данной кривой одну общую точку
Слайд 5ЦЕЛИ УРОКА:
1. Уточнить понятие касательной
к графику функции.
2. Вывести уравнение
касательной.
3. Создать алгоритм составления уравнения
касательной к графику функции y=f(x).
4. Начать
отрабатывать умения и навыкив составлении уравнения касательной в
различных
математических ситуациях.
Слайд 8Уравнение касательной
y = f(a) + f / (a) · (x
- a)
(a;f(a)) – координаты точки касания
f´(a) = tgα =k
– тангенс угла наклона касательной в данной точке или угловой коэффициент(х;у) – координаты любой точки касательной
Слайд 9Алгоритм
1. Обозначим абсциссу точки касания буквой а
2. Вычислим f(а)
3.
Найдем f´(x) и вычислим f´(а)
4. Подставим найденные значения в
общее уравнение касательной. 5. y = f(a) + f / (a) · (x - a)
Слайд 10Потренируемся:
Составить уравнение касательной к графику функции f(x)=x²-3x+5 в точке с
абсциссой а = -1
Слайд 11Самостоятельная работа Напишите уравнение касательной к графику функции у=f(x) в точке
с абсциссой а. вариант 1
вариант 2f(x) = х²+ х+1, а=1
f(x)= х-3х², а=2