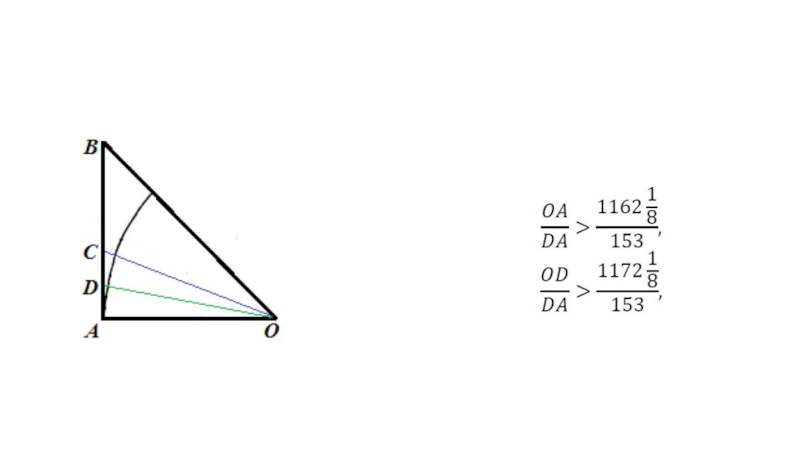Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о вписанном и центральном угле
Содержание
- 1. Теорема о вписанном и центральном угле
- 2. Теорема о вписанном и центральном углеВеличина вписанного
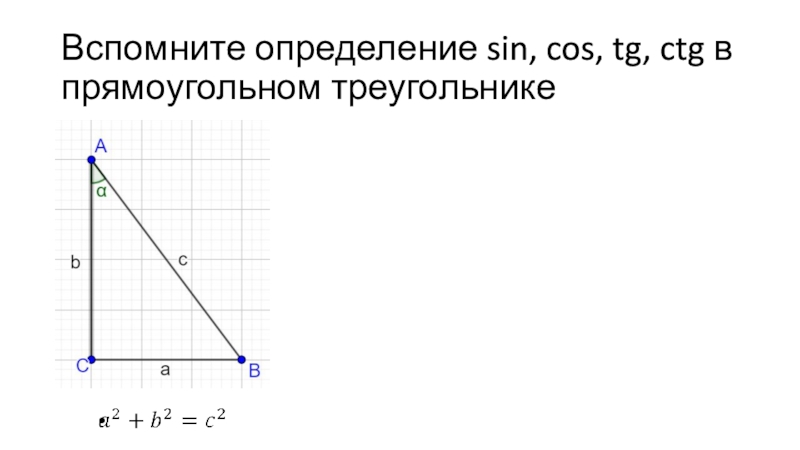
- 3. Вспомните определение sin, cos, tg, ctg в прямоугольном треугольнике
- 4. Единичная и координатная окружностьОпределение 1. Назовём единичной
- 5. Отображение координатной оси на координатную окружностьМножество R
- 6. свойства данного отображенияЕсли t-s=2*Pi*k, то им соответствует
- 7. Определение sin, cos, tg и ctg из
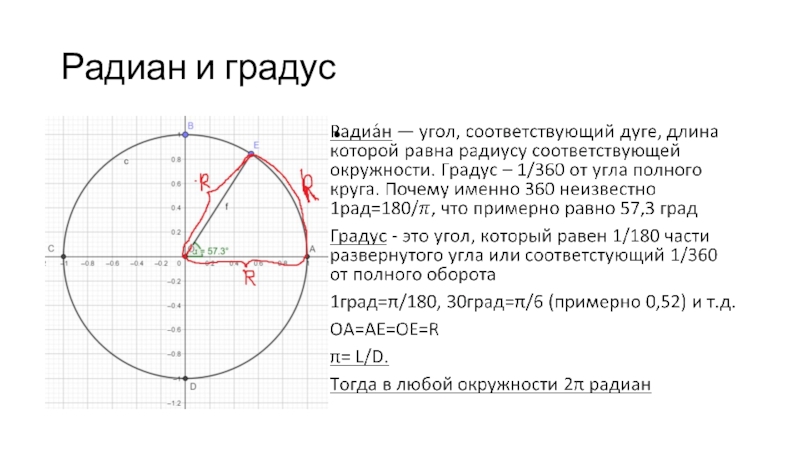
- 8. Длина окружности
- 9. Радиан и градус
- 10. Слайд 10
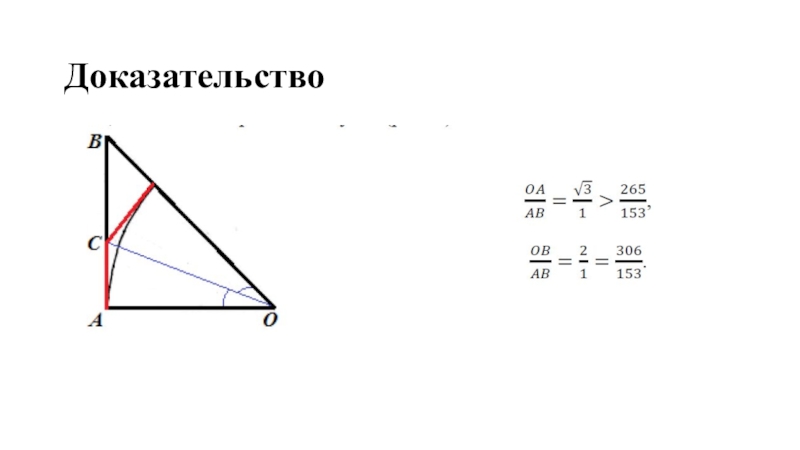
- 11. Доказательство
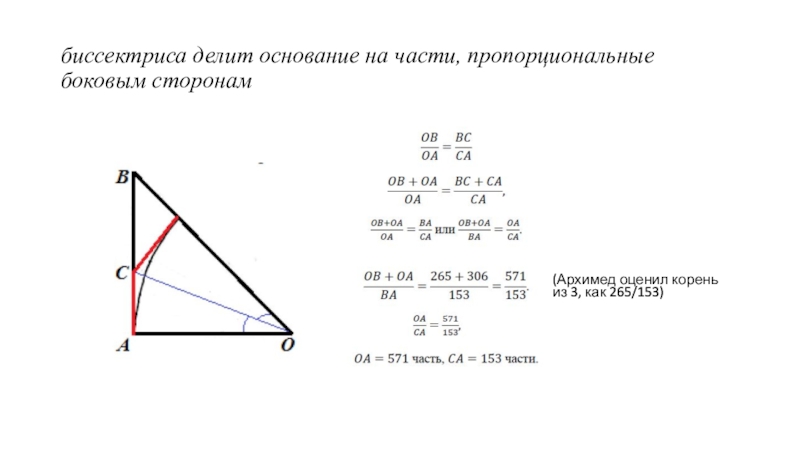
- 12. биссектриса делит основание на части, пропорциональные боковым сторонам (Архимед оценил корень из 3, как 265/153)
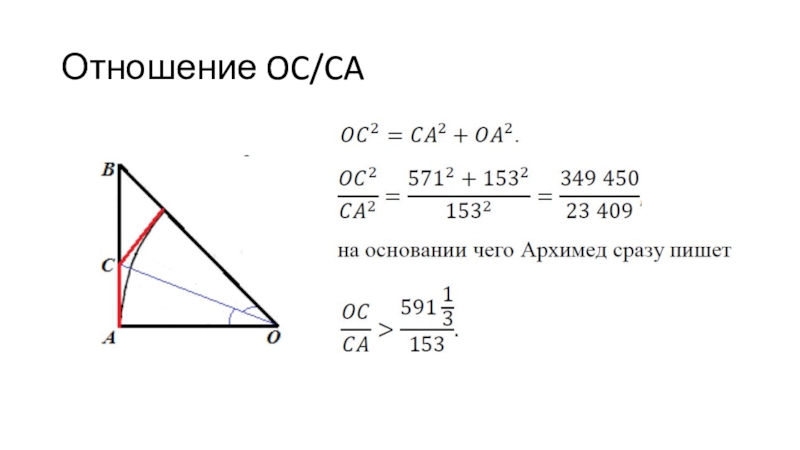
- 13. Отношение OC/CA
- 14. Слайд 14
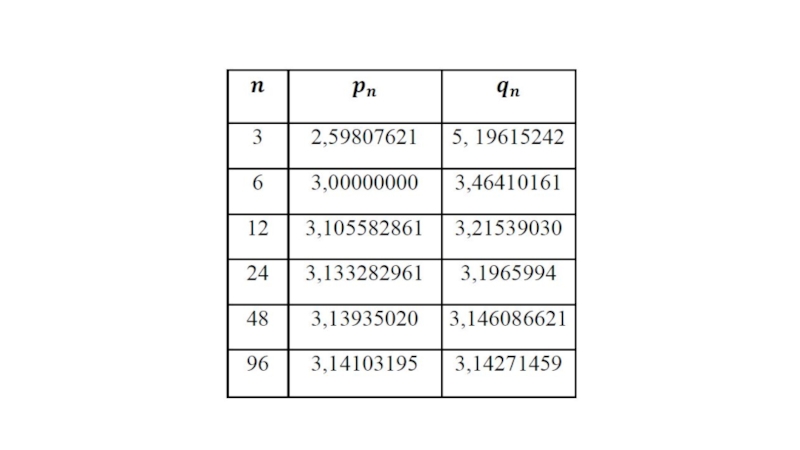
- 15. Отношение OA к полустороне 96-угольника
- 16. Определение нижнего предела1) Строим прямоугольный треугольник AA1B
- 17. От 6-угольника до 96-угольникаВ случае 6-угольника:Для 96-угольника:Последовательно
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
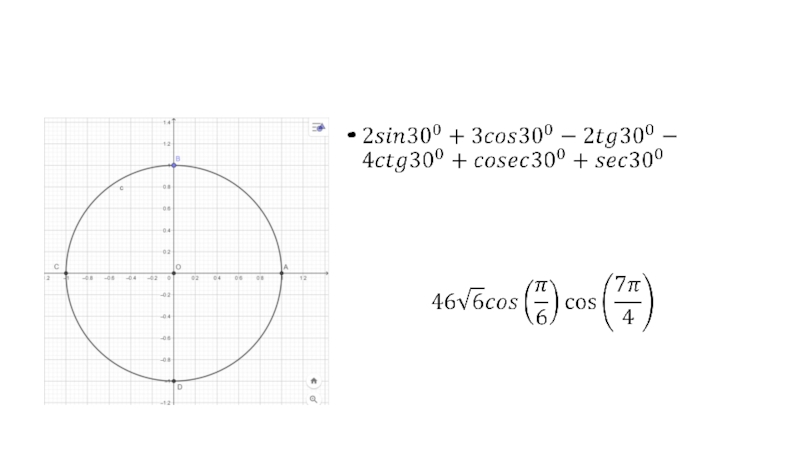
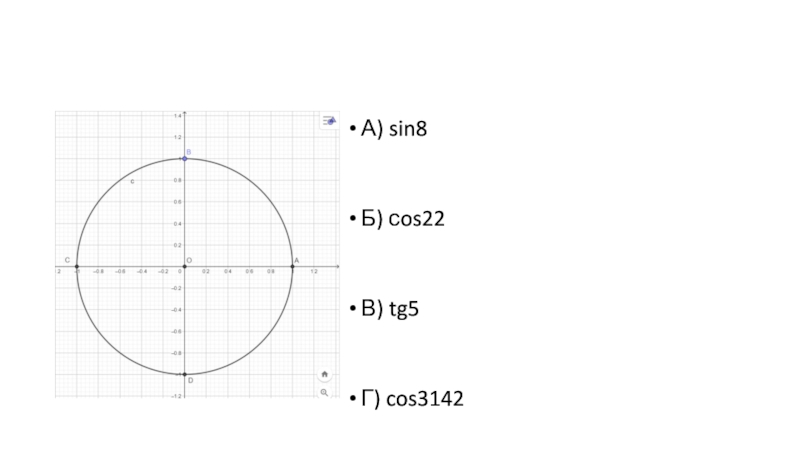
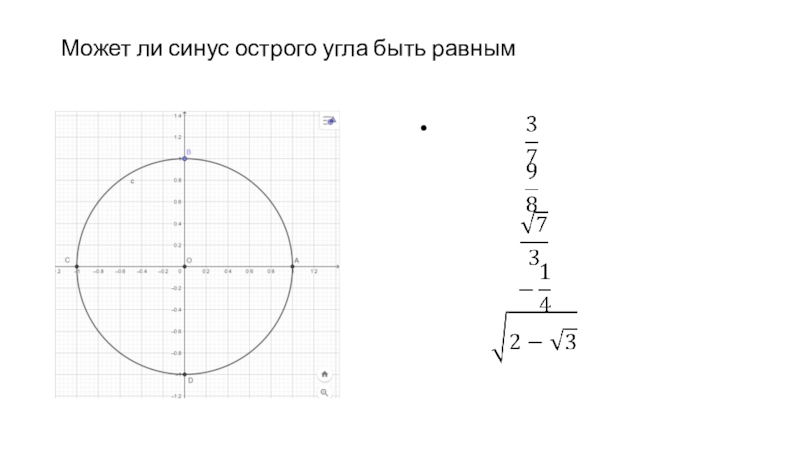
- 22. А) sin8Б) сos22В) tg5Г) cos3142
- 23. Слайд 23
- 24. Может ли синус острого угла быть равным
- 25. Скачать презентанцию
Теорема о вписанном и центральном углеВеличина вписанного угла равна половине центрального угла, опирающегося на ту же дугу.
Слайды и текст этой презентации
Слайд 1Теорема о вписанном и центральном угле
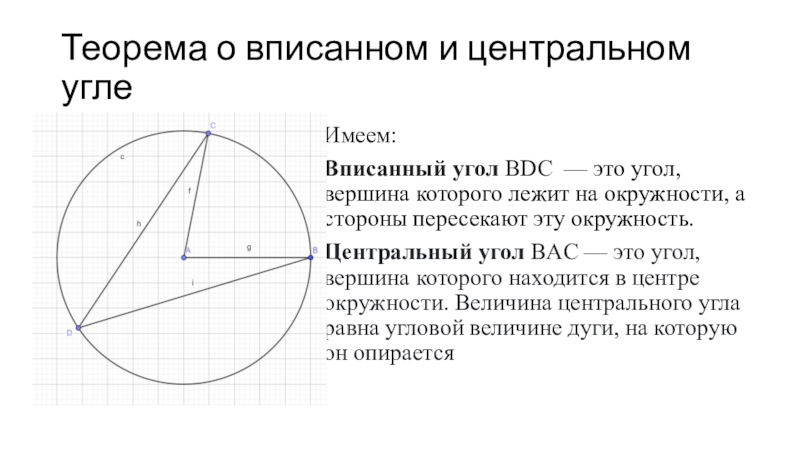
Имеем:
Вписанный угол BDC — это угол,
вершина которого лежит на окружности, а стороны пересекают эту окружность.
угол, вершина которого находится в центре окружности. Величина центрального угла равна угловой величине дуги, на которую он опираетсяСлайд 2Теорема о вписанном и центральном угле
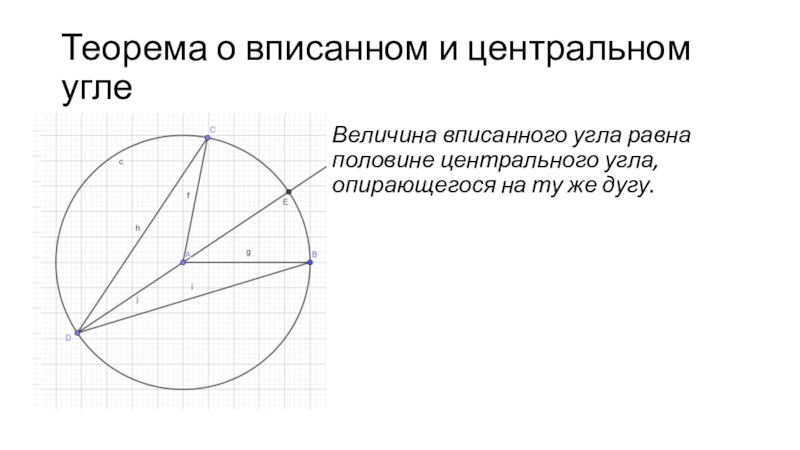
Величина вписанного угла равна половине
центрального угла, опирающегося на ту же дугу.
Слайд 4Единичная и координатная окружность
Определение 1. Назовём единичной окружностью окружность, радиус
которой равен масштабному отрезку (не указываем конкретную единицу измерения)
Определение 2.
Координатной окружностью называется окружность единичного радиуса, на которой выбраны начало отсчёта, направление обхода. Обычно положительное направление – против часовой стрелки.То есть задаётся система координат на окружности. Любая система координат состоит из начала отсчёта, единицы измерения длины, направления. Мы имеем одномерную систему координат c одной координатой, углом или длиной дуги от 0, можно задать точку на окружности т.е. провести отображение действительного числа на координатную окружность.
Слайд 5Отображение координатной оси на координатную окружность
Множество R разбиваем на промежутки
[2πn; 2π(n+1)] n – целое
Если t принадлежит промежутку [2πn;
2π(n+1)], то этой точке t ставим в соответствие точку на координатной окружности такую, что дуга AM, где A – начало отсчёта, равна t- 2πnСлайд 6свойства данного отображения
Если t-s=2*Pi*k, то им соответствует одна и та
же точка на координатной окружности
Точки M(t) и N(-t) симметричны
относительно прямой OA, где A – начало координат, O – центр окружностиТочки M(t) и N(t+π) диаметрально противоположны
Если |t-s|=|p-g|, то дуги TS=TG, где T=T(t) S=S(s) P=P(p) Q=Q(q)
Слайд 7Определение sin, cos, tg и ctg из тригонометрической окружности
Посмотрев на
то, чему равны тригонометрические функции в прямоугольном треугольнике, можно чисто
геометрически определить чему равны sin, cos, tg и ctg для каждой точки окружности, которой соответствует какой-то угол (угол является координатой точки на окружности).Таким образом, с учётом предыдущих рассуждений мы получили, что для каждой точки на числовой оси можно найти значение sin, cos, tg и ctg т.е. построили трингонометрические функции
Слайд 12биссектриса делит основание на части, пропорциональные боковым сторонам
(Архимед оценил
корень из 3, как 265/153)
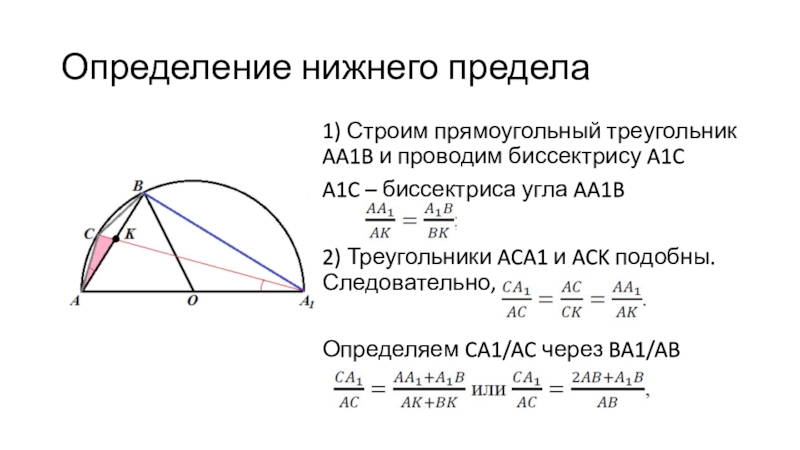
Слайд 16Определение нижнего предела
1) Строим прямоугольный треугольник AA1B и проводим биссектрису
A1C
A1C – биссектриса угла AA1B
2) Треугольники ACA1 и ACK подобны.
Следовательно,Определяем CA1/AC через BA1/AB

![Теорема о вписанном и центральном угле Отображение координатной оси на координатную окружностьМножество R разбиваем на промежутки [2πn; Отображение координатной оси на координатную окружностьМножество R разбиваем на промежутки [2πn; 2π(n+1)] n – целое Если t](/img/tmb/6/586784/a162e26e3e735bd1315f4e25af7013bd-800x.jpg)