Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Пифагора
Содержание
- 1. Теорема Пифагора
- 2. Содержание Формулировка теоремы Доказательства теоремы Значение теоремы Пифагора
- 3. Формулировка теоремы« Доказать, что квадрат, построенный
- 4. Современная формулировка« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 5. Доказательства теоремы Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
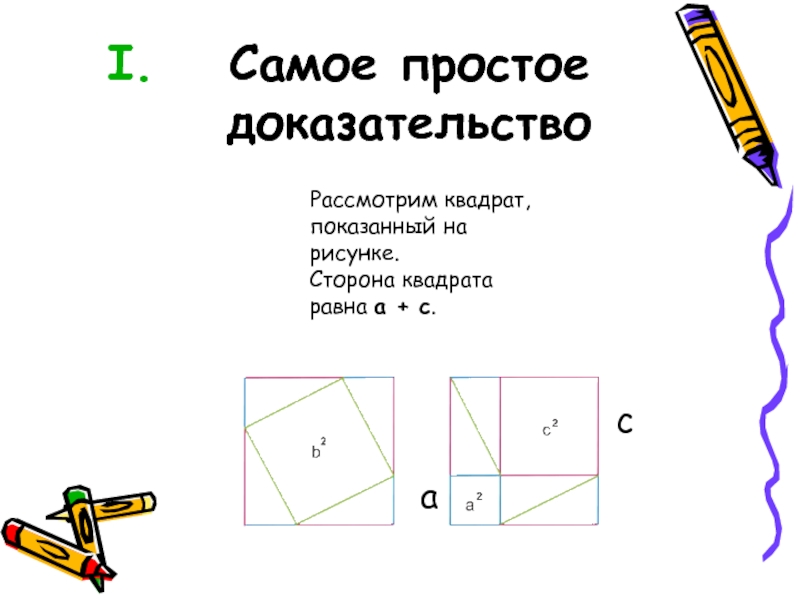
- 6. Самое простое доказательствоРассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c. ca
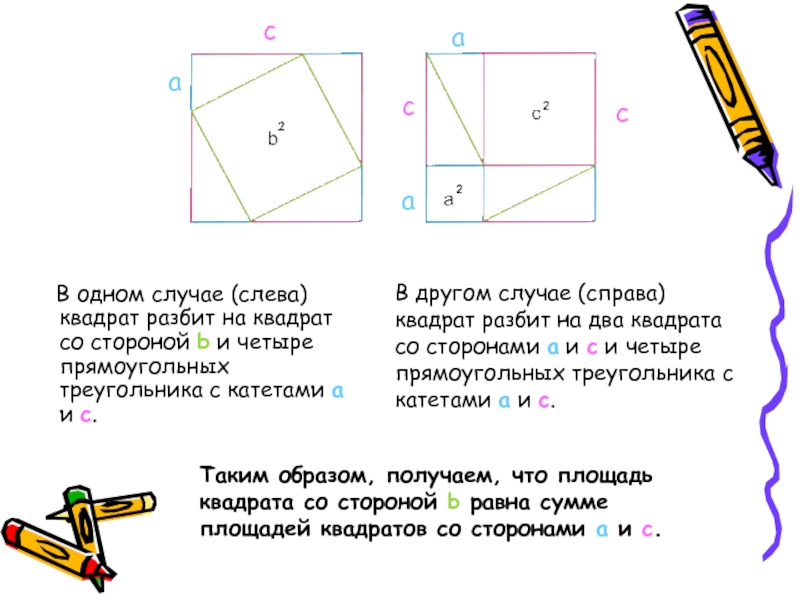
- 7. В одном случае (слева) квадрат
- 8. Геометрическое доказательство Дано: ABC-прямоугольный треугольникДоказать: BC2=AB2+AC2Доказательство: 1) Построим
- 9. Значение теоремы ПифагораТеорема Пифагора- это одна
- 10. Скачать презентанцию
Содержание Формулировка теоремы Доказательства теоремы Значение теоремы Пифагора
Слайды и текст этой презентации
Слайд 1Теорема Пифагора
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне
теорема Пифагора
Слайд 3Формулировка
теоремы
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника,
равновелик сумме квадратов, построенных на катетах»
« Площадь квадрата, построенного
на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах». Во времена Пифагора теорема звучала так:
или
Слайд 4Современная формулировка
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов».
Слайд 5Доказательства теоремы
Существует около 500 различных доказательств этой теоремы
(геометрических, алгебраических, механических и т.д.).
Слайд 6Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a
+ c.
c
a
Слайд 7
В одном случае (слева) квадрат разбит на квадрат
со стороной b и четыре прямоугольных треугольника с катетами a
и c.a
c
a
c
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
a
c
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
Слайд 8Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный отрезку
AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим
перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E. 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.
Слайд 9 Значение теоремы Пифагора
Теорема Пифагора- это одна из самых важных
теорем геометрии. Значение её состоит в том, что из неё
или с её помощью можно вывести большинство теорем геометрии.
