Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРЕМА ВАРИНЬОНА И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ
Содержание
- 1. ТЕОРЕМА ВАРИНЬОНА И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ
- 2. Предмет исследования --- планиметрические задачи ОБЪЕКТ ИССЛЕДОВАНИЯ
- 3. Цель: изучить теорему Вариньона и научиться на
- 4. Бимедианы четырехугольника – это отрезки, соединяющие середины противоположных сторон
- 5. ПЬЕР ВАРИНЬОН (1654-1722) Пьер Вариньон-
- 6. Теорема Вариньона Четырехугольник, образованный путем последовательного соединения
- 7. Теорема Вариньона Дано:ABCD- выпуклый
- 8. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ1. Центр параллелограмма
- 9. ТЕОРЕМА О БАБОЧКАХДоказательство. Воспользуемся теоремой о средней
- 10. Задачи из школьного курса геометрии.Рассмотрим задачи на
- 11. Конкурсные задачи.Все стороны выпуклого четырехугольника площади 1
- 12. Разбор задач с использованием теоремы Вариньона и
- 13. «Нет ничего нового под солнцем, но есть
- 14. Список использованной литературы1. Вавилов В., Красников П.
- 15. Слайд 15
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Предмет исследования --- планиметрические задачи
ОБЪЕКТ ИССЛЕДОВАНИЯ – ПАРАЛЛЕЛОГРАММ ВАРИНЬОНА,
БИМЕДИАНЫ ЧЕТЫРЕХУГОЛЬНИКА, ТЕОРЕМА ВАРИНЬОНА И СЛЕДСТВИЯ ИЗ НЕЁ
ПРОБЛЕМЫ – ВЫЯСНИТЬ,
ДЕЙСТВИТЕЛЬНО ЛИ ПАРАЛЛЕЛОГРАММ ВАРИНЬОНА ПОЗВОЛЯЕТ РАЦИОНАЛЬНЕЙ ПОЛУЧИТЬ РЕШЕНИЕ ЗАДАЧИГИПОТЕЗА ИССЛЕДОВАНИЯ – ПАРАЛЛЕЛОГРАММ ВАРИНЬОНА НАДЕЖНЫЙ ПОМОЩНИК В РЕШЕНИИ ЗАДАЧ
Слайд 3Цель: изучить теорему Вариньона и научиться на практике применять ее
с наименьшими временными затратами
ЗАДАЧИ:
А)Изучить теоретический материал: параллелограмм Вариньона, бимедианы четырехугольника
, теорему Вариньона и следствия из нее.Б)Сравнить количество времени, необходимое для решения задач традиционным способом и с помощью теоремы Вариньона.
В)Выяснить практическое применение данной теоремы в задачах по геометрии школьного курса и в конкурсных задачах.
Слайд 5ПЬЕР ВАРИНЬОН
(1654-1722)
Пьер Вариньон- французский математик, член Парижской
Академии наук, профессор математики колледжа Мазарини. Ему принадлежит одна из
основных теорем о бимедианах четырехугольника.Вариньон написал учебник по элементарной геометрии, в котором эта теорема впервые появилась.
Слайд 6Теорема Вариньона Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника,
является параллелограммом, и его площадь равна половине площади данного четырехугольника
Выпуклый
четырехугольникСамопересекающийся четырехугольник
Вогнутый четырехугольник
Слайд 7
Теорема Вариньона
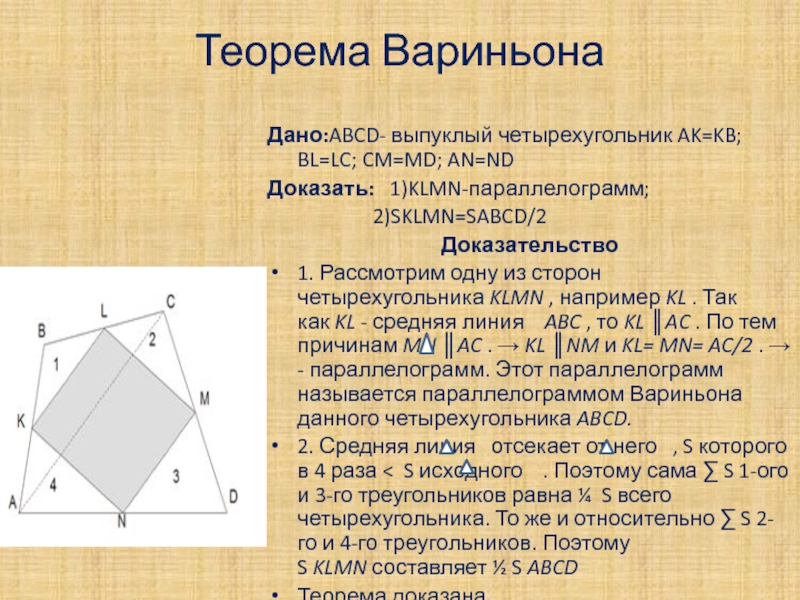
Дано:ABCD- выпуклый четырехугольник AK=KB; BL=LC; CM=MD; AN=ND
Доказать: 1)KLMN-параллелограмм;
2)SKLMN=SABCD/2
Доказательство
1. Рассмотрим одну из сторон четырехугольника KLMN , например KL . Так как KL - средняя линия ABC , то KL ║AC . По тем причинам MN ║AC . → KL ║NM и KL= MN= AC/2 . → KLMN - параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника ABCD.
2. Средняя линия отсекает от него , S которого в 4 раза < S исходного . Поэтому сама ∑ S 1-ого и 3-го треугольников равна ¼ S всего четырехугольника. То же и относительно ∑ S 2-го и 4-го треугольников. Поэтому S KLMN составляет ½ S ABCD
Теорема доказана.
Слайд 8СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ
1. Центр параллелограмма Вариньона лежит на
середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же
точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).2. Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.
3. Площадь параллелограмма Вариньона равна половине площади исходного четырёхугольника.
4. Для прямоугольника и равнобедренной трапеции параллелограммом Вариньона является ромб, а для ромба — прямоугольник.
Слайд 9ТЕОРЕМА О БАБОЧКАХ
Доказательство.
Воспользуемся теоремой о средней линии треугольника. Получаем:
Формулировка:
Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD
равны.Слайд 10Задачи из школьного курса геометрии.
Рассмотрим задачи на бимедианы четырехугольника и
теорему Вариньона, которые встречаются в школьном курсе геометрии (№567, 568)
Задача
1.Докажите, что а) середины сторон прямоугольника являются вершинами ромба. И наоборот, б) середины сторон ромба являются вершинами прямоугольника.
Доказательство.
а) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба;
Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба.
б) диагонали ромба перпендикулярны, поэтому середины сторон ромба являются вершинами прямоугольника;
Стороны ромба равны, поэтому середины сторон ромба являются вершинами прямоугольника.
Слайд 11Конкурсные задачи.
Все стороны выпуклого четырехугольника площади 1 разделены на 2n
равных частей, а затем точки деления на противоположных сторонах соединены
так, чтобы получилась «косоугольная шахматная доска», состоящая из белых и черных «клеток» (n = 2). Доказать, что сумма площадей всех белых «клеток» равна сумме площадей всех черных «клеток».ДОКАЗАТЕЛЬСТВО
Из следствия следует, что точки пересечения отрезков на этой доске делят каждый на равные части.
Тогда в любом «маленьком» четырехугольнике, куда входят ровно две белые и две черные клетки, выполняются условия теоремы о бабочках.
Нужное равенство установлено.
Слайд 12Разбор задач с использованием теоремы Вариньона и без её использования.
Докажите,
что середины сторон прямоугольника являются вершинами ромба. И наоборот.
1-ый способ
1-
AC – диагональ. FM - средняя линия треугольника ABC. NK – средняя линия треугольника ADC. Треугольники ABC и ADC равны по третьему признаку равенства треугольников (AB=DC, BC=AD, AC – общая сторона) => KN=FM. Также KN||FM (AC||FM, AC||KN) => KFMN- параллелограмм.
2- из первого следует, что KN=FM. Аналогично можно доказать, что FK=MN.
3- ABCD – прямоугольник => AC=BD. => KF=FM=MN=NK=> KFMN – ромб.
2-ой способ
А) Диагонали прямоугольника равны, поэтому середины сторон прямоугольника являются вершинами ромба (из следствия теоремы Вариньона);
Б) Стороны прямоугольника перпендикулярны, поэтому бимедианы перпендикулярны, тогда середины сторон прямоугольника являются вершинами ромба (из следствия теоремы Вариньона).
Слайд 13«Нет ничего нового под солнцем, но есть кое-что старое, чего
мы не знаем», – сказал американский литератор Лоренс Питер.
Пьер Вариньон
жил в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда, чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.Поэтому была поставлена цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.
Теорема Вариньона – красивейшая опорная задача, которая помогает решить, что называется, в один присест, массу планиметрических задач, в том числе повышенной сложности и олимпиадных.
Слайд 14Список использованной литературы
1. Вавилов В., Красников П. Бимедианы четырехугольника //
Математика . 2006 - №22.
2. Прасолов В.В. Задачи по планиметрии.
– Т.1,2 –М.: Наука, 19953. Штейнгауз Г. Математический калейдоскоп. - М.:Наука, 1981
4. BestReferat.ru// Бимедианы четырехугольника
5. dic.academic.ru// Что такое теорема о бабочках?
6. infourok.ru> issledovatelskaya… teorema variona // Исследовательская работа «Теорема Вариньона»
7. peoplе.su // Пьер Вариньон биография
8. referat.yabotanik.ru// бимедианы четырехугольника/ реферат по математике.
9. ru.vikipedia/org> Теорема Вариньона (геометрия)
10. treugolniki.ru>teorema-varinjоna// Лекции и примеры решения задач