Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоретическая (техническая) механика
Содержание
- 1. Теоретическая (техническая) механика
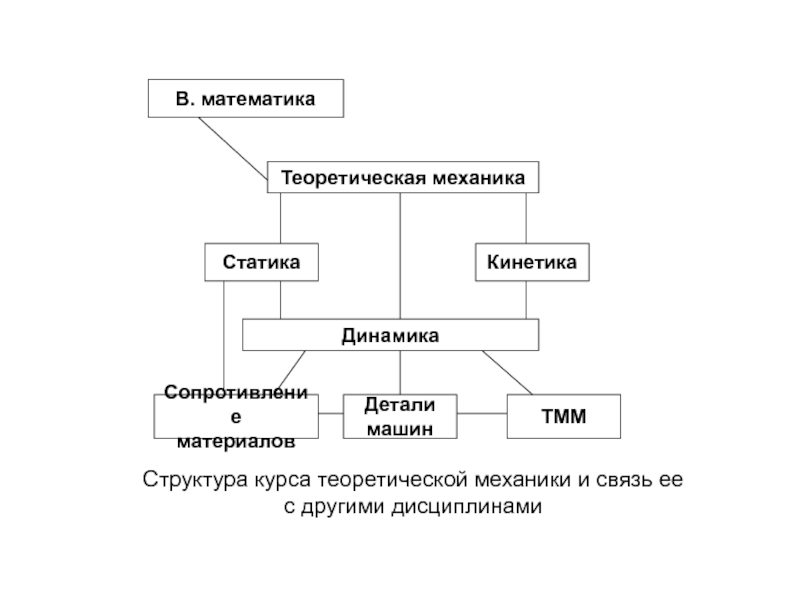
- 2. Структура курса теоретической механики и связь ее с другими дисциплинамиВ. математикаТеоретическая механикаСтатикаКинетикаДинамикаСопротивлениематериаловДеталимашинТММ
- 3. Теоретическая (классическая механика) - это наука, в
- 4. Сопротивление материалов –наука, в которой изучается
- 5. СТАТИКА Сила - это количественная
- 6. Система сил - это любая совокупность сил,
- 7. Слайд 7
- 8. 3. Аксиома параллелограмма.
- 9. Аксиома 4
- 10. 3. Связи и их реакции
- 11. Простейшие виды связей.Гибкая связь (нить, трос, цепь
- 12. 2. Гладкая (без трения) поверхность (опора). В
- 13. 3. Тонкий невесомый стержень с шарнирным закреплением
- 14. Одной из важных задач статики является определение
- 15. С силами, как и
- 16. Проекцией силы на ось называется скалярная величина,
- 17. Зная величины проекций силы на взаимно перпендикулярные
- 18. С помощью проекций можно находить
- 19. Слайд 19
- 20. Вторая задача статики - разработка условий равновесия.
- 21. Если все силы лежат в одной плоскости
- 22. Плоская произвольная ситема сипЭто система сил,
- 23. Для характеристики вращательного действия силы
- 24. Момент силы относительно точки равен
- 25. Слайд 25
- 26. Сумма сил пары равна нулю, поэтому пара
- 27. Эффект действия пары на твердое
- 28. Условия равновесия плоской произвольной системы сил
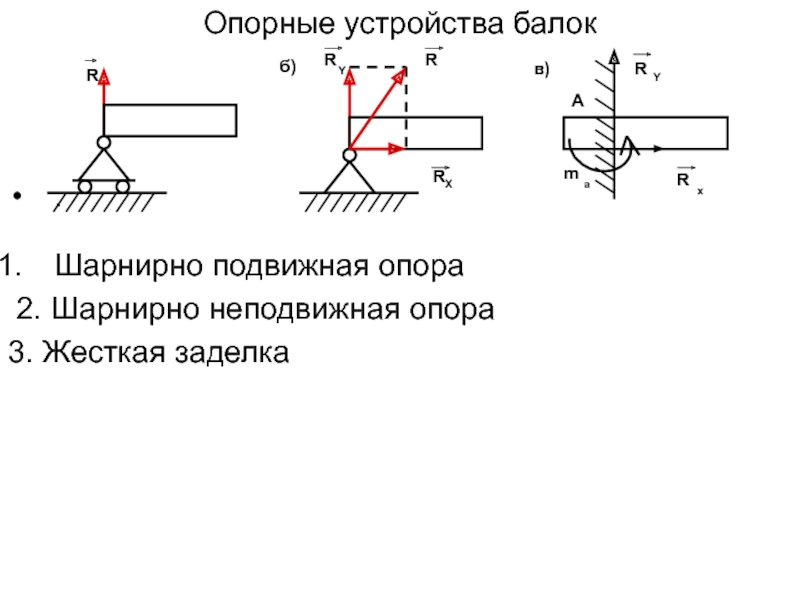
- 29. Опорные устройства балок. Шарнирно подвижная опора 2. Шарнирно неподвижная опора 3. Жесткая заделкаRRYRб)RXARYmaRxв)
- 30. Слайд 30
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Теоретическая (техническая) механика
Преподаватель:
Якубовская Светлана Васильевна
Механика - наука о движении и
равновесии материальных тел и взаимодействии между ними.
Слайд 2 Структура курса теоретической механики и связь ее с другими
дисциплинами
В. математика
Теоретическая механика
Статика
Кинетика
Динамика
Сопротивление
материалов
Детали
машин
ТММ
Слайд 3Теоретическая (классическая механика) - это наука, в которой изучаются общие
свойства движения и равновесия материальных тел.
В статике ( от
слова "статус"-покой) изучаются силы и законы равновесия материальных тел. Кинематика ( "кинема" - движение) изучает движение тел без учета действия сил, а динамика ("динамо"- сила в движении)- движение тел под действием сил.Слайд 4
Сопротивление материалов –наука, в которой изучается поведение твердых деформируемых
тел при различных видах нагружения
Задачи - инженерные методы расчета элементов
сооружений и машин на прочность, жесткость и устойчивость. Слайд 5СТАТИКА
Сила - это количественная мера взаимодействия материальных
тел.
Действие силы определяется тремя факторами: величиной
(модулем), направлением и точкой приложения, то есть сила является векторной величинойF
Слайд 6Система сил - это любая совокупность сил, действующая на данный
объект
Основные задачи статики:
1. Приведение данной системы сил к простейшему
виду (упрощение).2. Исследование условий равновесия данной системы сил.
Слайд 7
2. Аксиомы
статикиВсе уравнения статики выводятся из нескольких исходных положений - аксиом, то есть математически недоказуемых положений. Они представляют собой результаты обобщений практической деятельности.
1. Если на свободное твердое тело действуют две силы, то тело может находиться в равновесии, если эти силы равны по величине и направлены по одной прямой в разные стороны (рис.1.3).
2. Действие данной системы сил не изменится, если к ней добавить или от нее отнять уравновешенную систему сил.
=0 F = -F
F
F
2
1
1
2
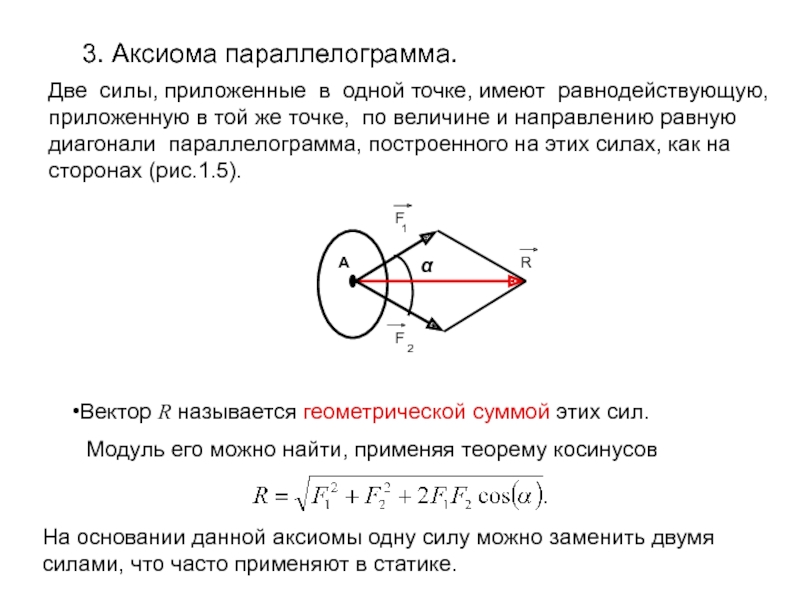
Слайд 8 3. Аксиома параллелограмма.
Вектор R
называется геометрической суммой этих сил.
Модуль его можно найти, применяя теорему
косинусовНа основании данной аксиомы одну силу можно заменить двумя силами, что часто применяют в статике.
Две силы, приложенные в одной точке, имеют равнодействующую, приложенную в той же точке, по величине и направлению равную диагонали параллелограмма, построенного на этих силах, как на сторонах (рис.1.5).
А
F
1
F
2
R
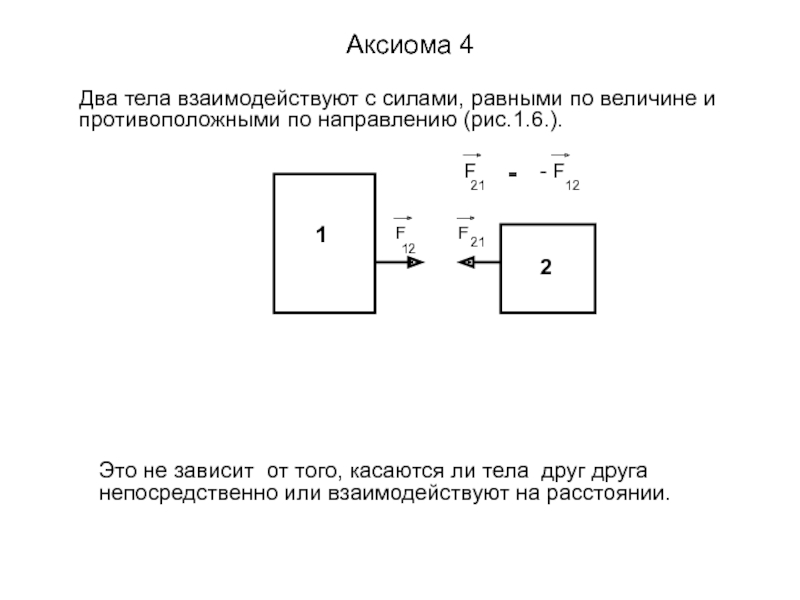
Слайд 9 Аксиома 4
Два
тела взаимодействуют с силами, равными по величине и противоположными по
направлению (рис.1.6.).Это не зависит от того, касаются ли тела друг друга непосредственно или взаимодействуют на расстоянии.
1
2
F
12
F
21
F
21
=
F
-
12
Слайд 10 3. Связи и их реакции
Рассматриваемые в
механике тела могут быть свободными и несвободными.
Свободным называется тело,
которое не связано с другими телами и может совершить из данного положения любое перемещение в пространстве. Тело, перемещение которого хотя бы в одном направлении ограничивается в пространстве другими телами, называется несвободным.
Тела, которые препятствуют перемещению данного тела , называются связями, а силы, с которыми связи действуют на это тело, - реакциями связей.
Реакция связи всегда направлена противоположно тому направлению, по которому связь препятствует перемещению тела.
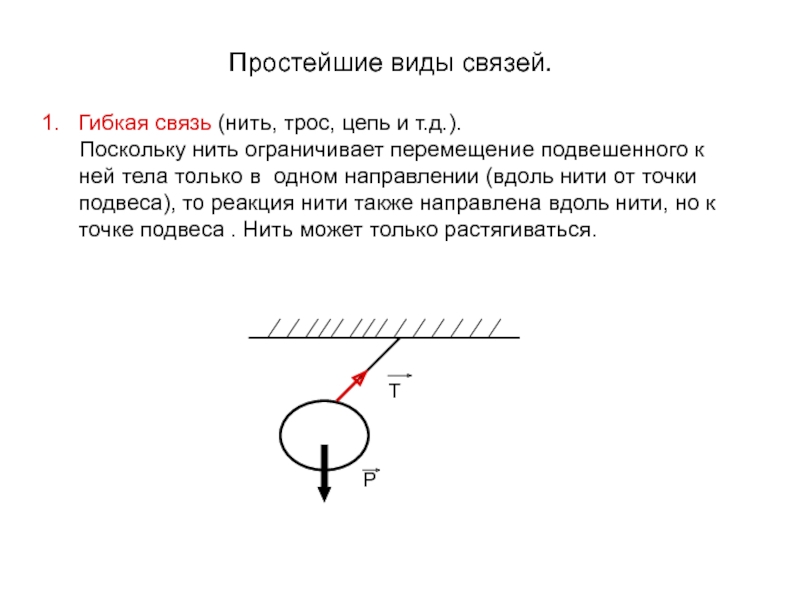
Слайд 11Простейшие виды связей.
Гибкая связь (нить, трос, цепь и т.д.).
Поскольку нить ограничивает перемещение подвешенного к ней тела
только в одном направлении (вдоль нити от точки подвеса), то реакция нити также направлена вдоль нити, но к точке подвеса . Нить может только растягиваться.P
T
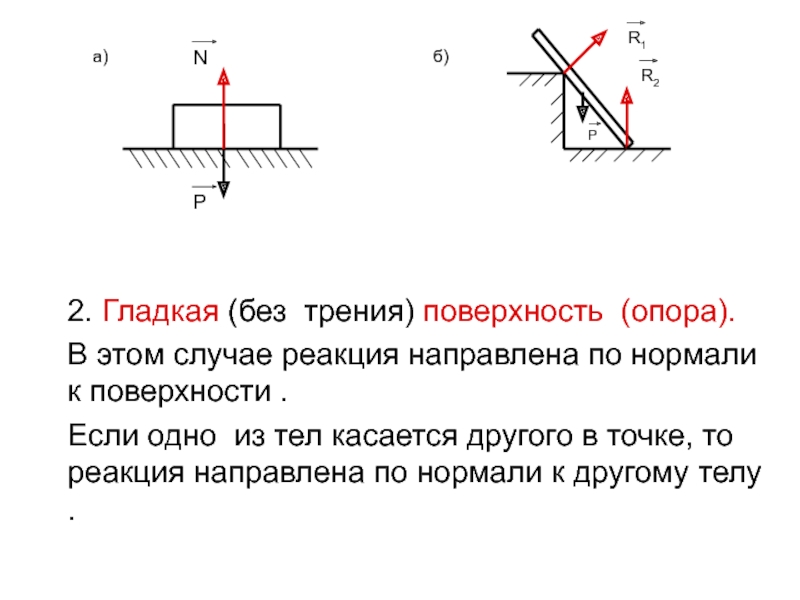
Слайд 122. Гладкая (без трения) поверхность (опора).
В этом случае реакция
направлена по нормали к поверхности .
Если одно из тел
касается другого в точке, то реакция направлена по нормали к другому телу .Р
N
а)
Р
R
1
R
2
б)
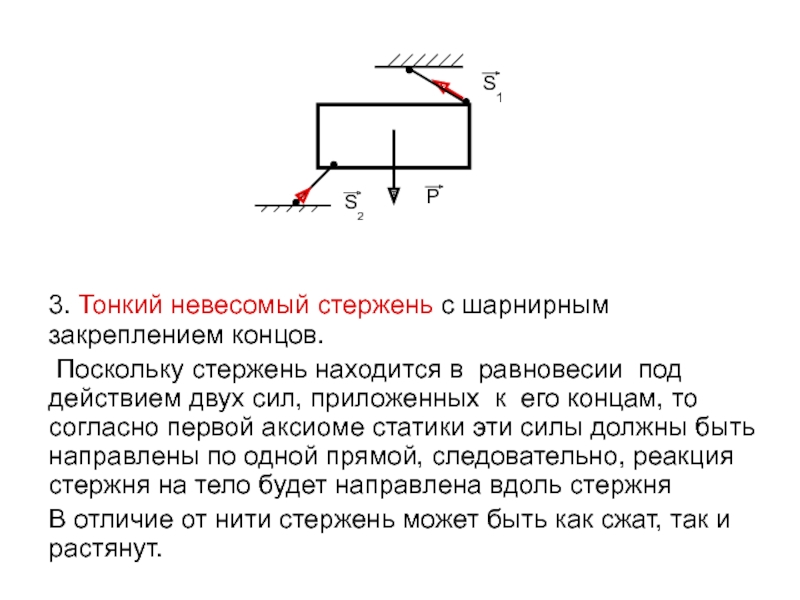
Слайд 133. Тонкий невесомый стержень с шарнирным закреплением концов.
Поскольку стержень
находится в равновесии под действием двух сил, приложенных к его
концам, то согласно первой аксиоме статики эти силы должны быть направлены по одной прямой, следовательно, реакция стержня на тело будет направлена вдоль стержняВ отличие от нити стержень может быть как сжат, так и растянут.
Р
S
2
S
1
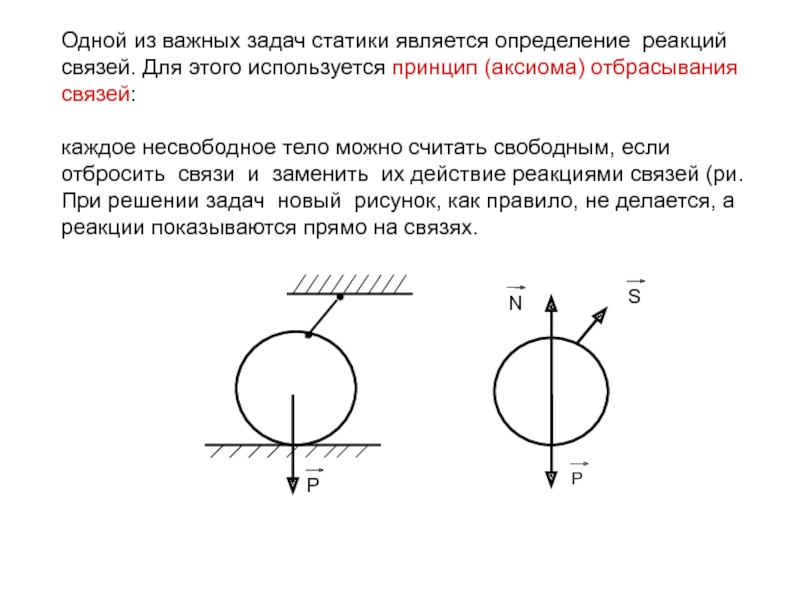
Слайд 14Одной из важных задач статики является определение реакций связей. Для
этого используется принцип (аксиома) отбрасывания связей:
каждое несвободное тело можно
считать свободным, если отбросить связи и заменить их действие реакциями связей (ри. При решении задач новый рисунок, как правило, не делается, а реакции показываются прямо на связях.Р
N
P
S
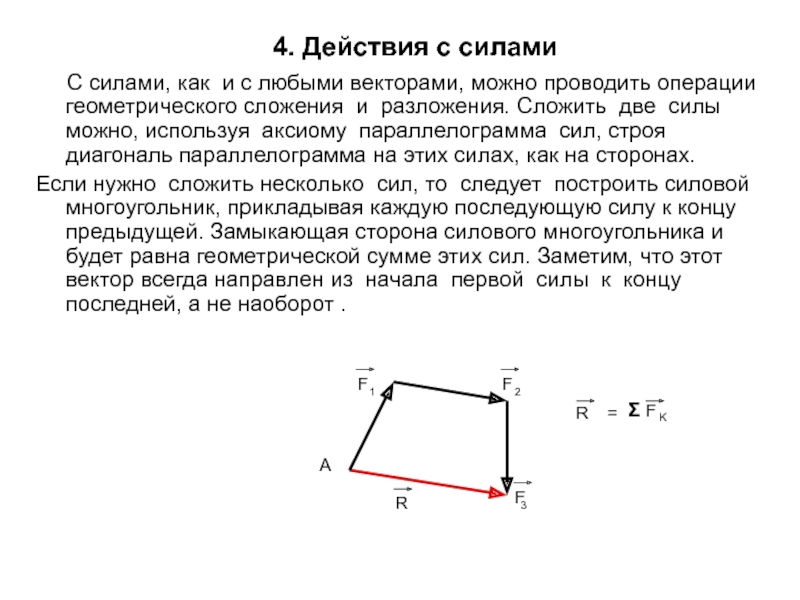
Слайд 15 С силами, как и с любыми векторами,
можно проводить операции геометрического сложения и разложения. Сложить две силы
можно, используя аксиому параллелограмма сил, строя диагональ параллелограмма на этих силах, как на сторонах.Если нужно сложить несколько сил, то следует построить силовой многоугольник, прикладывая каждую последующую силу к концу предыдущей. Замыкающая сторона силового многоугольника и будет равна геометрической сумме этих сил. Заметим, что этот вектор всегда направлен из начала первой силы к концу последней, а не наоборот .
4. Действия с силами
А
F
1
F
2
F
3
R
R
=
F
K
Слайд 16
Проекцией силы на ось называется скалярная величина, равная взятой с
соответствующим знаком длине отрезка, заключенного между проекциями начала и конца
вектора силы.Проекция считается положительной, если направление от начала к концу проекции совпадает с положительным направлением оси .
Проекция силы на ось равна произведению модуля силы на косинус угла между силой и положительным направлением оси.
а
b
O
A
F
Y
Y
B
F
F
X
X
Fx=Fcos
Слайд 17Зная величины проекций силы на взаимно перпендикулярные оси Х, У
и Z, модуль силы можно вычислить, как
Слайд 18 С помощью проекций можно находить не только силы,
но и сумму сил. Рассмотрим силы, строя векторный многоугольник, найдем
векторную сумму этих силИз рисунка видно, что проекция вектора суммы сил равна сумме проекций сил на эту же ось
Rx= F1x+F2x+F3x,
=Fкх.
F
1
F
1x
F
2x
F
3x
X
R
R
x
R
Y
Y
F
2
F
3
R
=
F
1
+
F
2
+
F
3
Ry =Fкy Rz =Fкz
Слайд 19
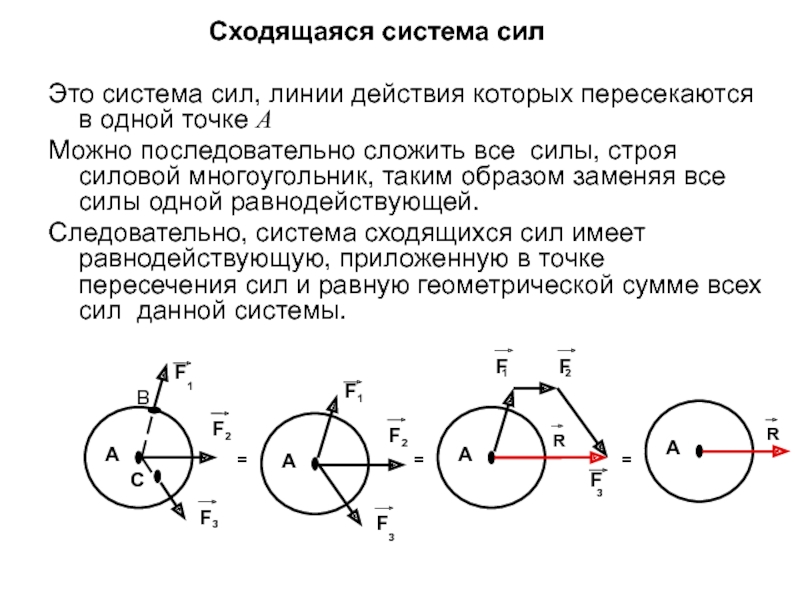
Сходящаяся система сил
Это система
сил, линии действия которых пересекаются в одной точке А Можно последовательно сложить все силы, строя силовой многоугольник, таким образом заменяя все силы одной равнодействующей.
Следовательно, система сходящихся сил имеет равнодействующую, приложенную в точке пересечения сил и равную геометрической сумме всех сил данной системы.
A
C
B
F
1
F
F
2
3
A
1
F
F
2
3
F
A
1
F
2
F
3
F
=
=
R
A
R
=
Слайд 20Вторая задача статики - разработка условий равновесия.
Они могут быть
получены в двух видах:
Геометрическое условие. Очевидно, что система сходящихся сил
будет эквивалентна нулю, если силовой многоугольник, построенный из сил системы, будет замкнут. Аналитическое условие. Величина равнодействующей будет равна нулю, если выполняются условия:
Fкx=0; Fкy=0; Fкz=0.
Слайд 21Если все силы лежат в одной плоскости (плоская сходящаяся система
сил), остаются два значащих уравнения
Fкx=0; Fкy=0.
Слайд 22
Плоская произвольная ситема сип
Это система сил, как угодно расположенных в
одной плоскости
Для данной системы нужно решить те-же задачи - упрощение
и изучение условий равновесияСлайд 23 Для характеристики вращательного действия силы вводится понятие момента
силы относительно точки.
Моментом силы относительно точки называется алгебраическая
величина, равная произведению модуля силы на кратчайшее расстояние между точкой и линией действия силы (плечо)Знак момента определяется следующим образом: если сила стремится повернуть тело вокруг данной точки против часовой стрелки, то он считается положительным , в противном случае - отрицательным.
Слайд 24 Момент силы относительно точки равен нулю только в
том случае, если линия действия силы проходит через данную точку.
Единицы измерения момента [HM] и в соответствующих кратных единицах..
Рис.1.20. Момент силы относительно точки
O
h
F
Слайд 25
Пара сил и ее свойства
Парой сил называется система, состоящая из
двух сил, равных по модулю, противоположных по направлению и не лежащих на одной прямой Плоскость, в которой лежат силы пары, называется плоскостью действия пары, а кратчайшее расстояние между силами пары называется плечом пары.
d
F
1
F
2
F
1
=
-
F
2
Слайд 26Сумма сил пары равна нулю, поэтому пара сил не имеет
равнодействующей, однако она оказывает на тело вращательное действие, характеризуемое ее
моментом.Моментом пары называется алгебраическая величина, модуль которой равен произведению одной из сил на плечо пары
m = F1d = F2 d.
Момент пары считается положительным, если пара стремится повернуть тело против часовой стрелки, и отрицательным, если пара стремится повернуть тело по часовой стрелке.
Слайд 27 Эффект действия пары на твердое тело не зависит
от ее положения в плоскости, поэтому ее можно переносить в
плоскости действия в любое положение. Кроме того, не изменяя действия пары на тело, ее можно заменить другой парой с равным моментом.Поэтому часто пары изображают в виде круговой стрелки и называют пару сосредоточенным моментом .
d
F
2
F
1
h
p
1
p
2
=
=
M
F d
1
=
P h
1
=
M
Слайд 28 Условия равновесия плоской произвольной системы сил
Для равновесия плоской
произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех
сил на оси Х и У и сумма моментов всех сил относительно произвольной точки были равны нулюFkx=0; Fky=0; m0=0.
- уравнения равновесия плоской системы сил.