Слайд 1Теоретические основы электротехники
Последовательность и методика
выполнения задачи №1
по курсовой работе
http://www.bestreferat.ru/referat-117052.html
Слайд 2Теоретические основы электротехники
Изменения к заданию для курсовой работы по дисциплине
«Теоретические
основы электротехники»
для учебных групп 21В, 22ВК и 43ППА
Рассмотрены и
обсуждены на заседании цикловой комиссии препода-
телей общетехнических дисциплин. Председатель ЦК А.И.Кейдо
Слайд 3Теоретические основы электротехники
Основные требования к текстовой документации
Слайд 4Основные требования к текстовой документации
Слайд 5Теоретические основы электротехники
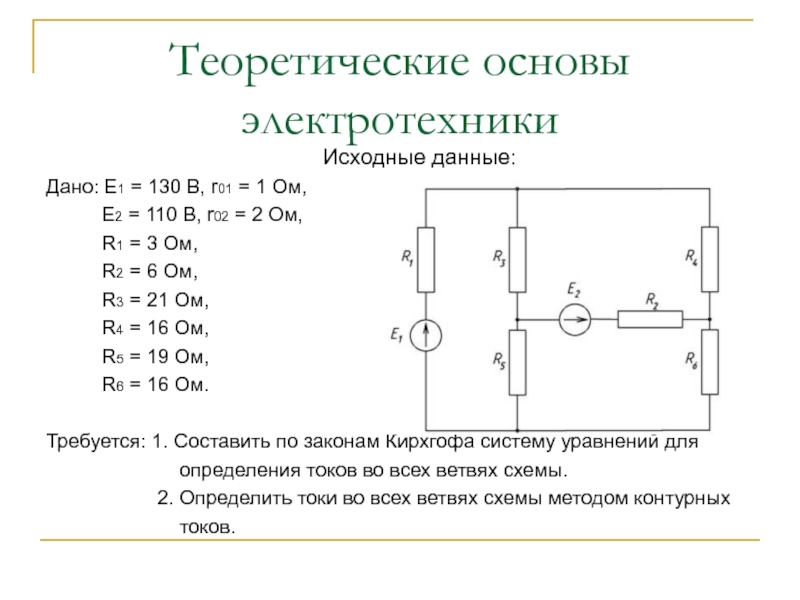
Исходные данные:
Дано: Е1 = 130 В, r01 =
1 Ом,
Е2 = 110 В,
r02 = 2 Ом,
R1 = 3 Ом,
R2 = 6 Ом,
R3 = 21 Ом,
R4 = 16 Ом,
R5 = 19 Ом,
R6 = 16 Ом.
Требуется: 1. Составить по законам Кирхгофа систему уравнений для
определения токов во всех ветвях схемы.
2. Определить токи во всех ветвях схемы методом контурных
токов.
Слайд 6Теоретические основы электротехники
Требуется:
3. Составить баланс мощности для заданной схемы.
4. Определить
токи во всех ветвях схемы на основании метода
наложения.
5. Результаты расчетов токов по пунктам 2 и 4 представить в виде
таблицы и сравнить.
6. Определить ток во второй ветви методом эквивалентного
генератора.
7. Построить потенциальную диаграмму для любого контура,
включающего обе ЭДС.
Слайд 7Теоретические основы электротехники
Выполнение
1. Составление по законам Кирхгофа системы уравнений для
определения токов во всех ветвях схемы
Обозначаем токи
ветвей и принимаем их направления на схеме, также
обозначаем узлы схемы.
В приведенной схеме 4 узла, значит
по первому закону Кирхгофа нужно
составить 3 уравнения:
Узел 1: I1 + I4 – I3 = 0.
Узел 2: I3 – I2 – I5 = 0.
Узел 3: I5 + I6 – I1 = 0.
Всего в схеме 6 ветвей и 6 неизвес-
тных токов – поэтому необходимо
составить шесть уравнений.
Слайд 8Теоретические основы электротехники
1. Составление по законам Кирхгофа системы уравнений для
определения токов во всех ветвях схемы
Недостающие 3 уравнения составляем по
второму закону Кирхгофа.
Для первого контура выберем обход по часовой
стрелке:
Е1 = I1(R1 + r01) + I5R5 + I3R3.
Для второго контура обход выберем против
часовой стрелки:
Е2 = I2(R2 + r02) + I4R4 + I3R3.
Для третьего контура направление обхода выберем по часовой стрелке:
Е2 = I2(R2 + r02) – I5R5 +I6R6.
Слайд 9Теоретические основы электротехники
1. Составление по законам Кирхгофа системы уравнений для
определения токов во всех ветвях схемы
В результате получили систему
из шести уравнений с шестью неизвестными токами:
I1 + I4 – I3 = 0
I3 – I2 – I5 = 0
I5 + I6 – I1 = 0
Е1 = I1(R1 + r01) + I5R5 + I3R3
Е2 = I2(R2 + r02) + I4R4 + I3R3
Е2 = I2(R2 + r02) – I5R5 +I6R6
Решив полученную систему уравнений можно определить токи во всех ветвях схемы.
Слайд 10Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом
контурных
токов
На схеме выбираем направления контурных токов I11, I22, I33,
направ- ления обхода контуров оставляем такими же как и направления токов.
Составляем уравнения для контурных
токов по второму закону Кирхгофа:
-Е1 = I11(R1 + r01 + R3 + R5) -I22R3 - I33R5
E2 = -I11R3 + I22(R2 + r02 + R3 + R4) - I33(R2 + r02)
-E2 = -I11R5 - I22(R2 + r02) + I33(R2 + r02 + R5 + R6)
В полученную систему уравнений
подставляем численные значения ЭДС и
сопротивлений.
Слайд 11Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом
контурных
токов
-130 = I11•(3 +1+21+19) - I22•21 - I33•19
110 = -I11•21 + I22•(6+2+21+16) - I33•(6+2)
-110 = -I11•19 - I22•(6+2) + I33•(6+2+19+16)
Выполнив сложения в скобках получим
следующую систему уравнений:
-130 = 44I11 – 21I22 – 19I33
110 = -21I11+ 45I22 – 8I33
-110 = -19I11 – 8I22 + 43I33
Решим полученную систему уравнений с помощью определителей.
Слайд 12Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом
контурных
токов
Вычисляем главный определитель системы
44 -21 -19
= -21 45 -8 = 44•45•43 + (-21)•(-8)•(-19) +
-19 -8 43 + (-19)•(-8)•(-21) – (-19)•45•(-19) –
- (-8)•(-8)•44 – 43•(-21)•(-21) = 40732
Вычисляем частные определители:
-130 -21 -19
11 = 110 45 -8 =(-130)•45•43 + (-21)(-8)(-110)+
-110 -8 43 +(-19)(-8)•110 – (-110)•45•(-19) –
- (-8)(-8)(-130) – 43•110(-21) = -239710
Слайд 13Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом
контурных
токов
Вычисляем частные определители для контурных токов второго и третьего
контуров:
44 -130 -19
22 = -21 110 -8 = 44•110•43 + (-130)(-8)(-19)+
-19 -110 43 + (-19)(-110)(-21) – (-19)•110•(-19) -
– (-110)(-8)•44 – 43•(-21)(-130) = -51390
44 -21 -130
33 = -21 45 110 = 44•45•(-110) + (-21)110(-19) +
-19 -8 -110 + (-130)(-8)(-21) – (-19)45(-130) -
- (-8)110•44 – (-110)(-21)(-21) = - 219670
Слайд 14Теоретические основы электротехники
2. Определить токи во всех ветвях схемы методом
контурных токов
Определяем контурные токи:
I11 = 11 / = -239710 / 40732 = -5,885 A,
I22 = 22 / = -51390 / 40732 = -1,262 A,
I33 = 33 / = -219670 / 40732 = -5,393 A.
Определяем токи ветвей
I1 = -I11 = 5,885 A,
I2 = I22 – I33 = -1,262 - (-5,393) = 4,131 A,
I3 = I22 – I11 = -1,262 - (-5,885) = 4,623 A,
I4 = I22 = -1,262 A,
I5 = I33 – I11 = -5,393 - (-5,885) = 0,493 A,
I6 = -I33 = 5,393 A.
Слайд 15Теоретические основы электротехники
3. Составление баланса мощности для заданной схемы
Cоставим баланс мощности
Мощность источников:
Ри = Е1 • I1 + E2 • I2 = 130 • 5,885 + 110 • 4,131 =
= 1219,46 Вт.
Мощность приемников:
Р = I1²(R1 + r01) + I2²(R2 + r02) + I3²R3 + I4²R4 + I5²R5 +
+ I6²R6 =
= 5,885² • (3 + 1) + 4,131² • (6 + 2) + 4,623² • 21 + (-1,262)² • 16 +
+ 0,493² • 19 + 5,393² • 16 = 1219,32 Вт.
Таким образом, Ри = 1219,46 Вт Р = 1219,32 Вт – баланс мощности подтверждается – ошибка в расчетах составляет:
(Ри – Р) / Ри = (1219,46 – 1219,32) / 1219,46 = 0,000115•100% = 0,0115%.
Слайд 16Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на
основании метода наложения
Определим частичные токи ветвей под действием источника
Е1.
Для этого исключим из схемы источник Е2, а вместо его оставим внутреннее сопротивление источника r02. Нанесем на схеме частичные токи от ЭДС Е1 и обозначим их с одним штрихом (I). Решаем задачу методом
«свертывания», но для этого предва-
рительно заменим звезду сопротивле-
ний R4 – R6 – R202 треугольником.
Определим сопротивления сторон
треугольника:
R4202 = R4 + R202 + R4 • R202 / R6 =
= 16 + (6+2) + 16 • (6+2) / 16 = 32 Ом,
R6202 = R6 + R202 + R6 • R202 / R4 =
= 16 + (6+2) + 16 • (6+2) / 16 = 32 Ом,
Слайд 17Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на
основании метода
наложения
R46 = R4 + R6 + R4 • R6 / R202 =
= 16 + 16 + 16 • 16 / (6+2) = 64 Ом.
Определим эквивалентные сопротивле-
ния параллельно соединенных резисторов:
R34202 = R3 • R4202 / (R3 + R4202) =
= 21 • 32 / (21 + 32) = 12,679 Ом,
R56202 = R5 • R6202 / (R5 + R6202) =
= 19 • 32 / (19 + 32) = 11,922 Ом.
Определим сопротивление последовательно соединенных резисторов
R3546202 = R34202 + R56202 = 12,679 + 11,922 = 24,601 Ом.
Определим эквивалентное сопротивление относительно первой ветви
R1-3 = R3546202 • R46 / (R3546202 + R46) = 24,601 • 64 / (24,601 + 64) = 17,77Ом.
Слайд 18Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на
основании метода
наложения
Определим частичный ток в первое ветви
I1 = E1 / (R1-3 + R1 + r01) = 130 / (17,77 + 3 + 1) = 5,972 A.
Определим ток в последовательном участке
I35-46 = I1 • R46 / (R3546202 + R46) =
= 5,972 • 64 / (24,601 + 64) = 4,314 A.
Определим частичные токи в третьем и пятом
резисторах
I3=I35-46•R4202/(R3+R4202)=4,314•32/(21+32)=2,605 А,
I5=I35-46•R6202/(R5+R6202)=4,314•32/(19+32)=2,707 А.
Для определения частичных токов в остальных ветвях схемы с источником Е1 вернемся к исходной схеме с этим источником.
Слайд 19Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на
основании метода
наложения
Определим частичные токи во второй,
четвертой и шестой ветвях на основании
первого закона Кирхгофа:
I4 = I1 – I3 = 5,972 – 2,605 = 3,367 A,
I6 = I1 – I5 = 5,972 – 2,707 = 3,265 A,
I2 = I3 – I5 = 2,605 – 2,707 = -0,102 A.
Для определения частичных токов от
действия источника Е2 исключаем из схемы
источник Е1, вместо него включаем
внутреннее сопротивление и частичные
токи обозначаем с двумя штрихами.
Слайд 20Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на
основании метода
наложения
Частичные токи определяем методом «сворачивания»
схемы, но предварительно треугольник сопротивлений
(R1+r01), R3, R5 заменяем эквивалентной звездой.
Тогда схема будет иметь вид.
Определим сопротивления лучей звезды:
R3101 = R3 • R101 / (R3 + R101 + R5) =
= 21 • (3+1) / (21 + 3 + 1 + 19) = 1,909 Ом,
R5101 = R5 • R101 / (R3 + R101 + R5) =
= 19 • (3+1) / (21 + 3 + 1 + 19) = 1,727 Ом,
R35 = R3 • R5 / (R3 + R101 + R5) =
= 21 • 19 / (21 + 3 + 1 + 19) = 9,068 Ом.
Слайд 21Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на
основании метода
наложения
Определим эквивалентное сопротивление цепи относительно источника Е2:
Rэ =
(R3101 + R4) • (R5101 + R6) / (R3101 + R4 + R5101 + R6) + R35 + R2 =
= (1,909 + 16) • (1,727 + 16) / (1,909 + 16 + 1,727 + 16) + 9,068 + 6 = 23,977 Ом.
Определим ток в ветви с источником
I2 = E2 / (Rэ + r02) = 110 / (23,977 + 2) = 4,235 А.
Определим токи в четвертой и шестой ветвях
I4 = I2 • (R5101 + R6) / (R3101 + R4 + R5101 + R6) =
= 4,235 • (1,727 + 16) / (1,909 + 16 + 1,727 + 16) = 2,107 A
I6 = I2 • (R3101 + R4) / (R3101 + R4 + R5101 + R6) =
= 4,235 • (1,909 + 16) / (1,909 + 16 + 1,727 + 16) = 2,128 A
Для определения токов в первой, третьей и пятой ветвях возвращаемся к исходной схеме с источником Е2.
Слайд 22Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на
основании метода
наложения
Определим потенциалы первого и третьего узлов,
принимая потенциал четвертого узла равным нулю:
1 = -I4 • R4 = -2,107 • 16 = -33,712 B,
3 = -I6 • R6 = -2,128 • 16 = -34,048 B.
Определим напряжение между третьим и первым узлами:
U31 = 3 - 1 = -34,048 – (-33,712) = -0,336 B.
Определим частичный ток в первой ветви при действии источника Е2
I1 = U31 / (R1 + r01) = -0,336 / (3 + 1) = -0,084 A.
Для определения токов в третьей и пятой ветвях воспользуемся первым законом Кирхгофа: I3 = I1 + I4 = -0,084 + 2,107 = 2,023 A,
I5 = I6 - I1 = 2,128 – (-0,084) = 2,212 A.
Слайд 23Теоретические основы электротехники
4. Определить токи во всех ветвях схемы на
основании метода
наложения
Определяем токи ветвей:
I1 = I1 + I1 =
5,972 – 0,084 = 5,888 А, I2 = I2 + I2 = -0,102 + 4,235 = 4,133 А,
I3 = I3 + I3 = 2,605 + 2,023 = 4,628 А, I4 = I4 - I4 = 2,107 – 3,367 = -1,26 А,
I5 = I5 - I5 = 2,707 – 2,212 = 0,495 А, I6 = I6 + I6 = 3,265 +2,128 = 5,393 А.
Слайд 24Теоретические основы электротехники
5. Результаты расчетов токов по пунктам 2 и
4 представить в виде
таблицы и сравнить
Метод расчёта
Ток
в ветви
Слайд 25Теоретические основы электротехники
6. Определить ток во второй ветви методом эквивалентного
генератора
Для определения эквивалентной ЭДС Еэ или напряже-
ния холостого хода Uо исключаем во второй ветви резис-
тор R2, оставляем ветвь разомкнутой с зажимами а и б и
определяем напряжение между этими зажимами, которое
и называется напряжением холостого хода.
Для определения Uо рассчитаем токи I01, I05 и I06
R3546 = (R3 + R5) • (R4 + R6) / (R3 + R5 + R4 + R6) =
= (21 + 19)•(16 + 16) / (21 + 19 + 16 + 16) = 17,778 Ом,
I01 = Е1 / (R3546 + R1 +r01) =130/(17,778+3+1)=5,969 A
I05 = I01 • (R4 + R6) / (R3 + R5 + R4 + R6) =
= 5,969 • (16 + 16) / (21 + 19 + 16 + 16) = 2,653 A,
I06 = I01 • (R3 + R5) / (R3 + R5 + R4 + R6) =
= 5,969 • (21 + 19) / (21 + 19 + 16 + 16) = 3,316 A.
Слайд 26Теоретические основы электротехники
6. Определить ток во второй ветви методом эквивалентного
генератора
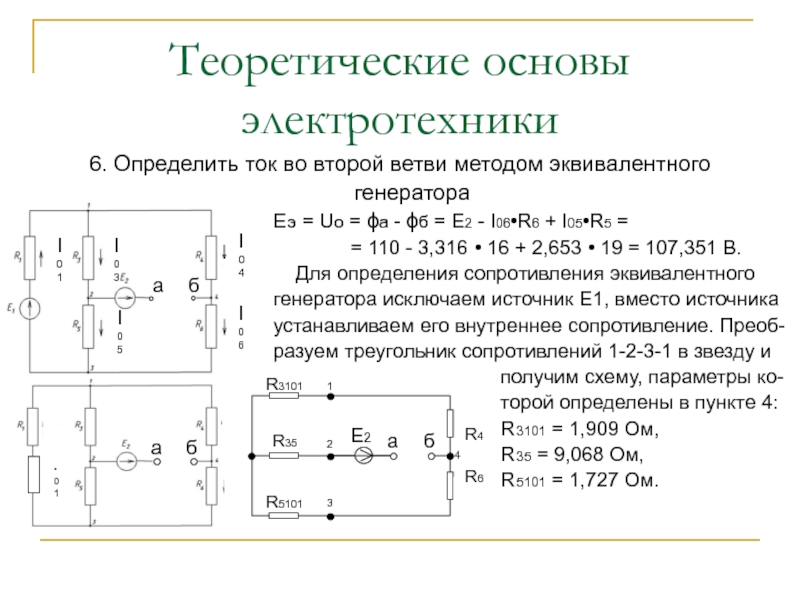
Eэ = Uo = a - б = Е2 - I06•R6 + I05•R5 =
= 110 - 3,316 • 16 + 2,653 • 19 = 107,351 B.
Для определения сопротивления эквивалентного
генератора исключаем источник Е1, вместо источника
устанавливаем его внутреннее сопротивление. Преоб-
разуем треугольник сопротивлений 1-2-3-1 в звезду и
получим схему, параметры ко-
торой определены в пункте 4:
R3101 = 1,909 Ом,
R35 = 9,068 Ом,
R5101 = 1,727 Ом.
E2
Слайд 27Теоретические основы электротехники
6. Определить ток во второй ветви методом эквивалентного
генератора
Тогда сопротивление эквивалентного генератора
составит:
rэ = (R3101 + R4)•(R5101 + R6)/(R3101 + R4 + R5101 + R6) + R35 +
+ r02 = (1,909+16)•(1,727+16)/(1,909+16+1,727+16) +
+ 9,068 + 2 = 19,977 Ом.
Определяем ток во второй ветви схемы:
I2 = Eэ / (rэ + R2) = 107,351 / (19,977 + 6) = 4,133 А.
Таким образом, при расчете методом эквивалентного
генератора ток во второй ветви получился таким же, как и
при расчете методом контурных токов и методом
наложения.
E2
Слайд 28Теоретические основы электротехники
7. Построить потенциальную диаграмму для любого контура,
включающего обе ЭДС
Для построения потенциальной диаграммы выбираем контур с двумя
источниками питания. Такому условию соответствует контур, отмеченный на ниж-
нем рисунке.
Выбираем в качестве начального узел 1 и придаем ему
потенциал, равный нулю. Для расчета потенциалов осталь-
ных точек обходим контур по часовой стрелке. Тогда:
1 = 0,
4 = 1 + I4 • R4 = 0 + (-1,262 • 16) = -20,2 B,
5 = 4 + I2 • R2 = -20,2 + 4,131 • 6 = 4,6 B,
2 = 5 - E2 + I2• r02 = 4,6 - 110 + 4,131 • 2 = -97,1 B,
3 = 2 – I5• R5 = -97,1 – 0,493 • 19 = -106,5 B,
6 = 3 + E1 – I1 • r01 = -106,5 + 130 – 5,885 • 1 = 17,6 B,
1 = 6 – I1 • R1 = 17,6 – 5,885 • 3 = -0,06 B – проверочная
точка.
Слайд 29Теоретические основы электротехники
7. Построить потенциальную диаграмму для любого контура,
включающего обе ЭДС
По полученным данным строим для контура потенциальную диаграмму
- зависимость потенциалов точек от сопротивлений участков контура.
Слайд 30Теоретические основы электротехники
Последовательность и методика
выполнения задачи №2
по курсовой работе
Слайд 31Теоретические основы электротехники
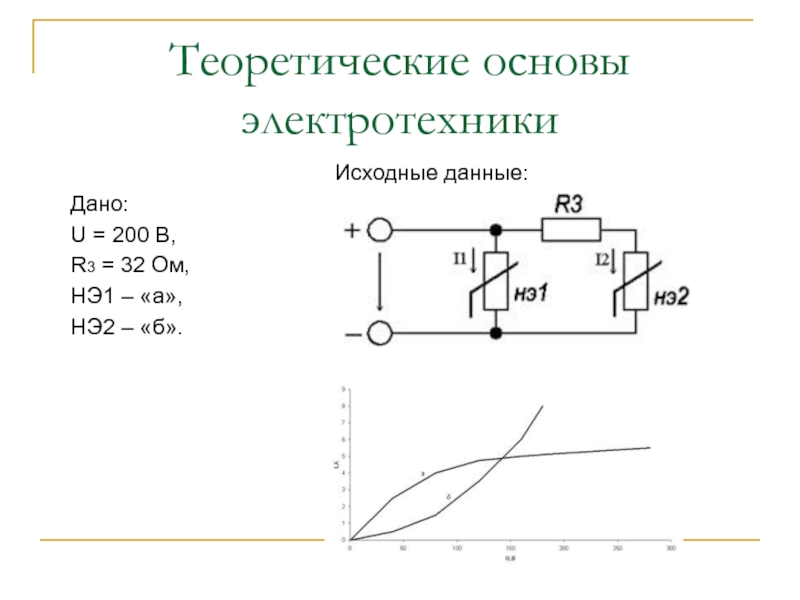
Исходные данные:
Дано:
U = 200 B,
R3 = 32 Ом,
НЭ1
– «а»,
НЭ2 – «б».
Слайд 32Теоретические основы электротехники
Требуется:
1. Определить графическим методом все токи.
2. Определить напряжения
на всех участках цепи.
Р е ш е н и е
1.
Расчет цепи производим графическим методом. Для этого в общей системе координат (U,I) строим заданные вольт-амперные характеристики нелинейных элементов (НЭ1 и НЭ2).
Для построения характеристик принимаем масштабы:
Для напряжений Mu = 25 B/cм.
Для токов MI = 1 A/cм.
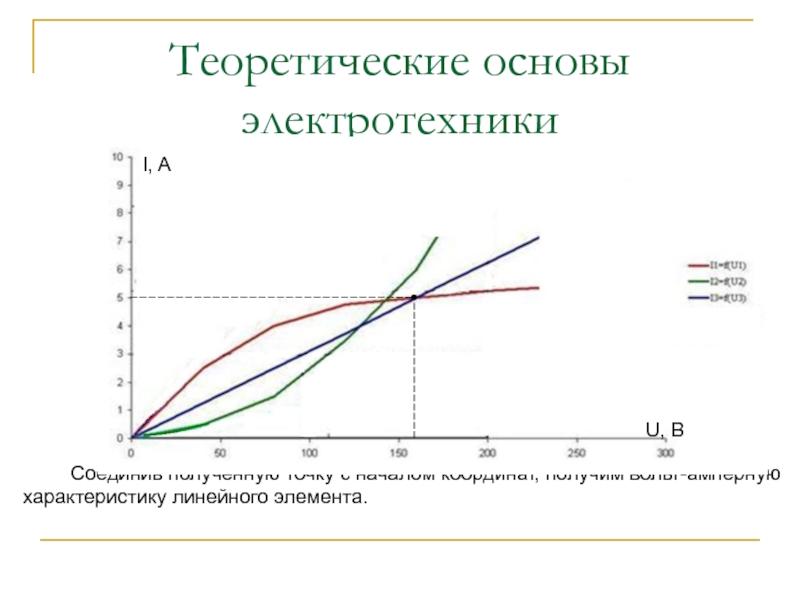
Для построения вольт-амперной характеристики линейного элемента (R3) определим координаты одной из точек характеристики. Пусть абсциссой этой точки будет U = 160 B. Тогда ордината этой точки составит:
I = U / R3 = 160 / 32 = 5 A.
Слайд 33Теоретические основы электротехники
Р е ш е н и е
Соединив полученную
точку с началом координат, получим вольт-амперную характеристику линейного элемента.
Слайд 34Теоретические основы электротехники
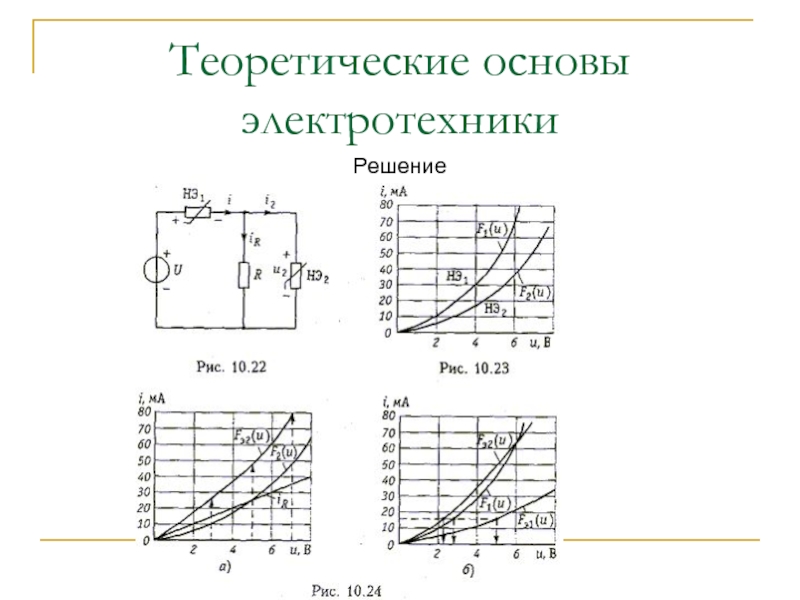
Решение
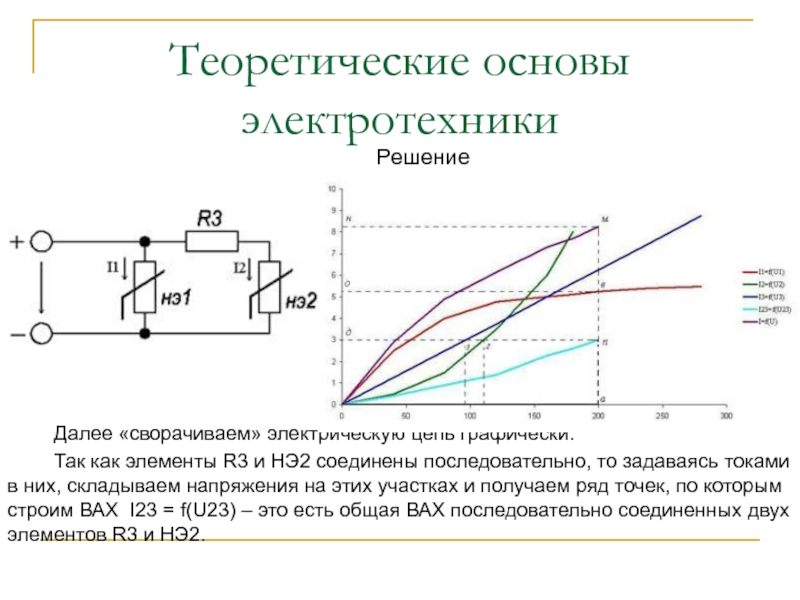
Далее «сворачиваем» электрическую цепь графически.
Так как элементы R3
и НЭ2 соединены последовательно, то задаваясь токами в них, складываем
напряжения на этих участках и получаем ряд точек, по которым строим ВАХ I23 = f(U23) – это есть общая ВАХ последовательно соединенных двух элементов R3 и НЭ2.
Слайд 35Теоретические основы электротехники
Решение
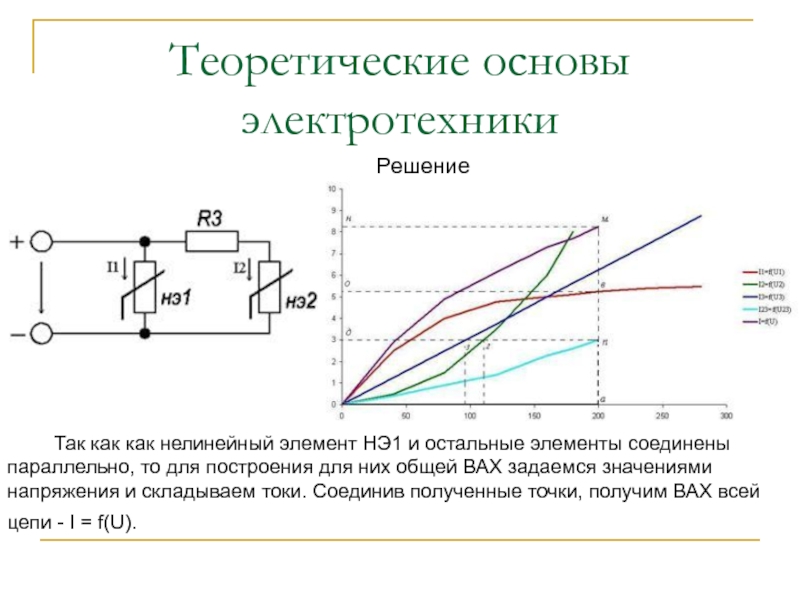
Так как как нелинейный элемент НЭ1 и остальные
элементы соединены параллельно, то для построения для них общей ВАХ
задаемся значениями напряжения и складываем токи. Соединив полученные точки, получим ВАХ всей цепи - I = f(U).
Слайд 36Теоретические основы электротехники
Решение
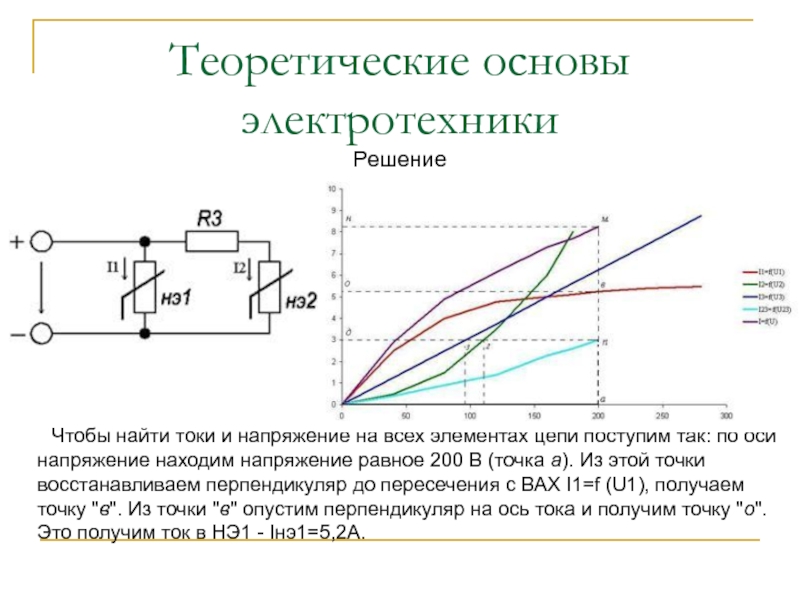
Чтобы найти токи и
напряжение на всех элементах цепи поступим так: по оси напряжение
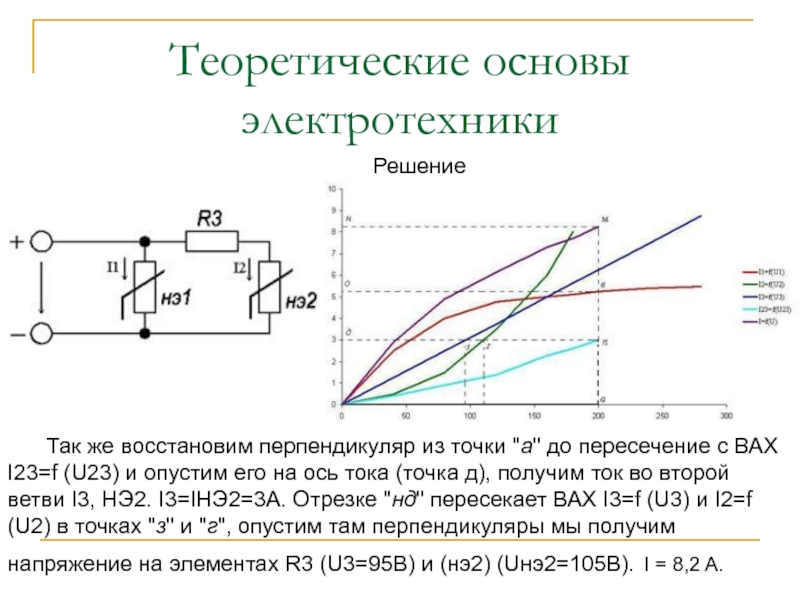
находим напряжение равное 200 В (точка а). Из этой точки восстанавливаем перпендикуляр до пересечения с ВАХ I1=f (U1), получаем точку "в". Из точки "в" опустим перпендикуляр на ось тока и получим точку "о". Это получим ток в НЭ1 - Iнэ1=5,2А.
Слайд 37Теоретические основы электротехники
Решение
Так же восстановим перпендикуляр из точки "а" до
пересечение с ВАХ I23=f (U23) и опустим его на ось
тока (точка д), получим ток во второй ветви I3, НЭ2. I3=IНЭ2=3А. Отрезке "нд" пересекает ВАХ I3=f (U3) и I2=f (U2) в точках "з" и "г", опустим там перпендикуляры мы получим напряжение на элементах R3 (U3=95В) и (нэ2) (Uнэ2=105В). I = 8,2 A.
Слайд 38Теоретические основы электротехники
Решение
Слайд 40Теоретические основы электротехники
Последовательность и методика
выполнения задачи №4
по курсовой работе
Слайд 41Теоретические основы электротехники
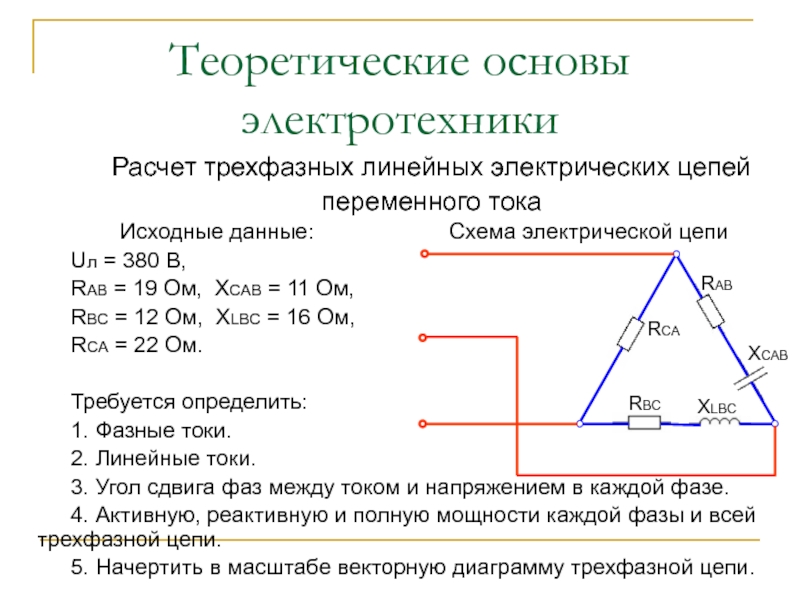
Расчет трехфазных линейных электрических цепей
переменного тока
Исходные данные:
Схема электрической цепи
Uл = 380 B,
RAB = 19 Ом, XCAB = 11 Ом,
RBC = 12 Ом, XLBC = 16 Ом,
RCA = 22 Ом.
Требуется определить:
1. Фазные токи.
2. Линейные токи.
3. Угол сдвига фаз между током и напряжением в каждой фазе.
4. Активную, реактивную и полную мощности каждой фазы и всей трехфазной цепи.
5. Начертить в масштабе векторную диаграмму трехфазной цепи.
Слайд 42Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока
Решение
Для расчета
трехфазной цепи применим символический метод.
1. При соединении нагрузки треугольником модули
фазных напряжений равны линейным напряжениям:
Uф = Uл = 380 B, то есть UAB = UBC = UCA = 380 B.
2. Комплексы данных напряжений запишем из условия, что вектор фазного напряжения UАВ совпадает с действительной осью комплексной плоскости:
Слайд 43Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока
Решение
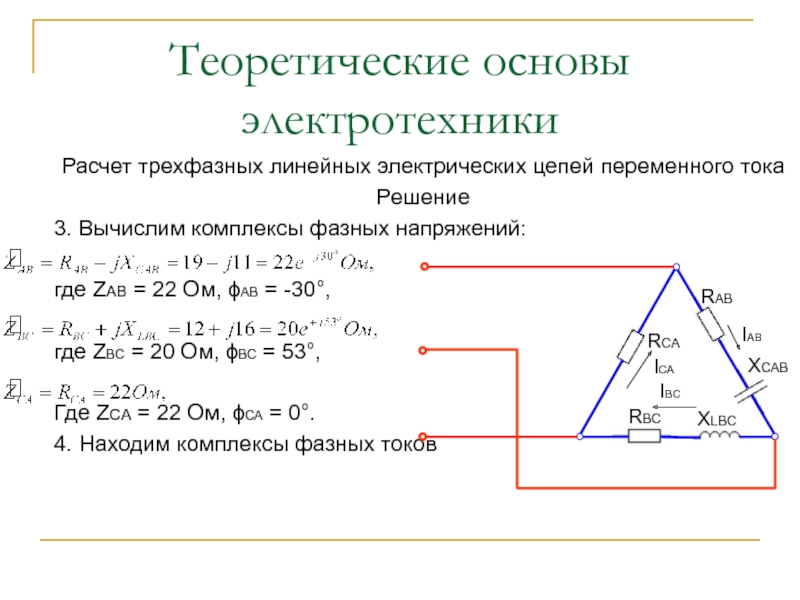
3. Вычислим
комплексы фазных напряжений:
где ZAB = 22 Ом, АВ = -30,
где
ZBC = 20 Ом, ВС = 53,
Где ZCA = 22 Ом, СА = 0.
4. Находим комплексы фазных токов
Слайд 44Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока
Решение
4. Находим
комплексы фазных токов
модуль IAB = 17,27 A, AB = 30,
модуль
IВС = 19 A, BC = -173,
модуль ICA = 17,27 A, СА = 120.
Слайд 45Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока
Решение
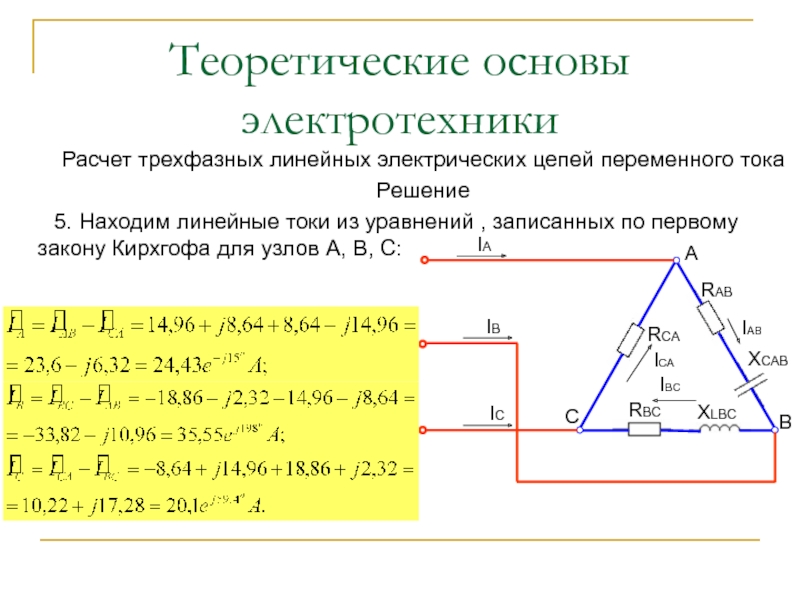
5. Находим
линейные токи из уравнений , записанных по первому закону Кирхгофа
для узлов А, В, С:
Слайд 46Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока
Решение
6.Вычисляем мощность
каждой фазы и всей цепи
Слайд 47Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока
Решение
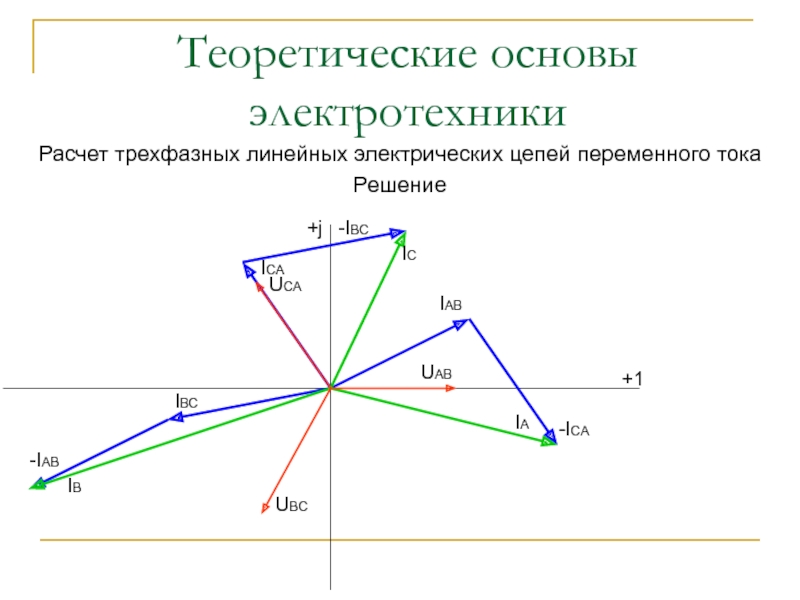
7. Строим
в масштабе векторную диаграмму напряжений и токов.
Выбираем масштабы напряжений и
токов:
Mu = 100 B/cм, Mi = 4 A/cм.
Векторы фазных токов IAB, IBC, ICA строим под углами АВ, ВС, СА к действительной оси.
К концам векторов IAB, IBC, ICA пристраиваем отрицательные фазные токи согласно уравнениям: Замыкающие векторные
треугольники векторов IAB, IBC, ICA
представляют в выбранном
масштабе линейные токи.
Слайд 48Теоретические основы электротехники
Расчет трехфазных линейных электрических цепей переменного тока
Решение
Слайд 49Теоретические основы электротехники
Расчет однофазной цепи
Исходные данные:
Схема электрической цепи
R1
= 10 Ом, R2 = 20 Ом,
L1 = 38 мГн, L2 = 25 мГн,
C1 = 45 мкФ, C2 = 198 мкФ,
Um = 65 B, u = 45,
f = 50 Гц.
Требуется
1. Определить токи отдельных участков цепи.
2. Написать уравнение изменения тока источника питания цепи.
3. Составить баланс мощности.
4. Построить векторную диаграмму токов и топографическую диаграмму напряжений.
Слайд 50Теоретические основы электротехники
Слайд 51Теоретические основы электротехники