Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теоретические основы электротехники
Содержание
- 1. Теоретические основы электротехники
- 2. ОбщееТрудоемкость дисциплины: 6 з.е. (216 часов)Аудиторные занятия
- 3. Контрольная работаРасчет электрических цепей постоянного тока.Расчет однофазных
- 4. Требования к предъявлению контрольной работыВыполняется свой вариант
- 5. Определение варианта задач контрольной работыНомер варианта -
- 6. Определение варианта задач контрольной работыНомер варианта -
- 7. Определение варианта задач контрольной работыНомер варианта -
- 8. Основные моменты дисциплиныЧто надо знать, чтобы не получить неудовлетворительную отметку?
- 9. Основные законы электрических цепей постоянного тока Закон
- 10. Закон Ома для участка цепи без источника
- 11. Обобщенный закон Ома (для участка цепи с ЭДС)
- 12. Обобщенный закон Ома (для участка цепи с ЭДС)
- 13. I закон КирхгофаАлгебраическая сумма токов в узле
- 14. II закон КирхгофаАлгебраическая сумма падений напряжений любого
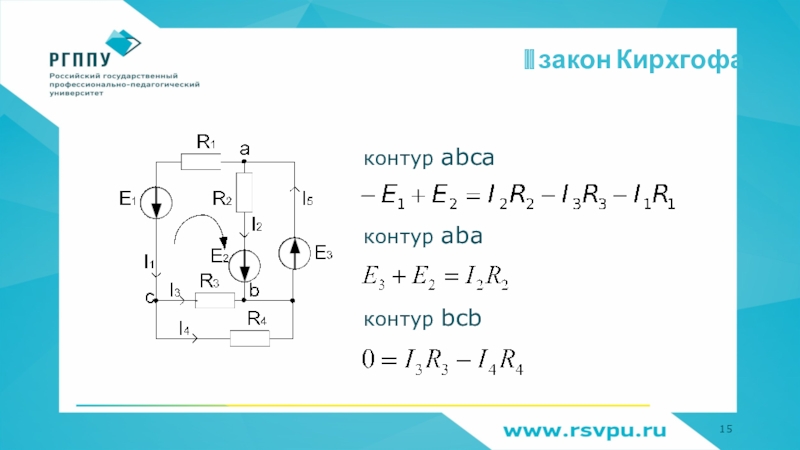
- 15. II закон Кирхгофаконтур abca контур aba контур bcb
- 16. Метод преобразования цепиПоследовательное соединение резисторов Ток во всех последовательно соединенных элементах одинаков
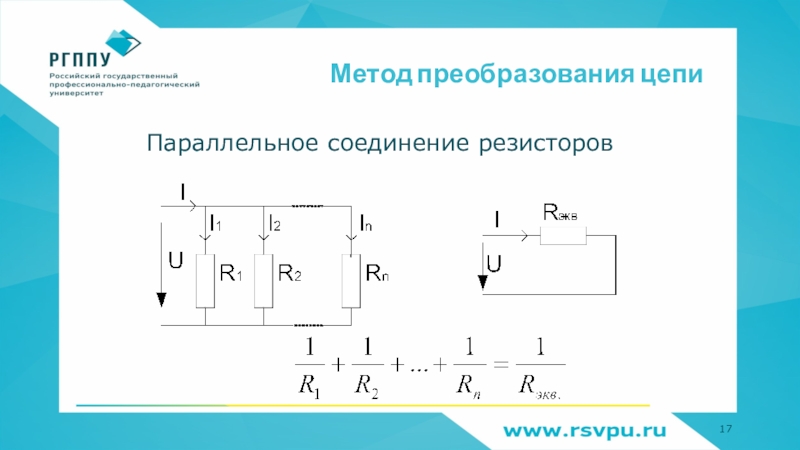
- 17. Метод преобразования цепиПараллельное соединение резисторов
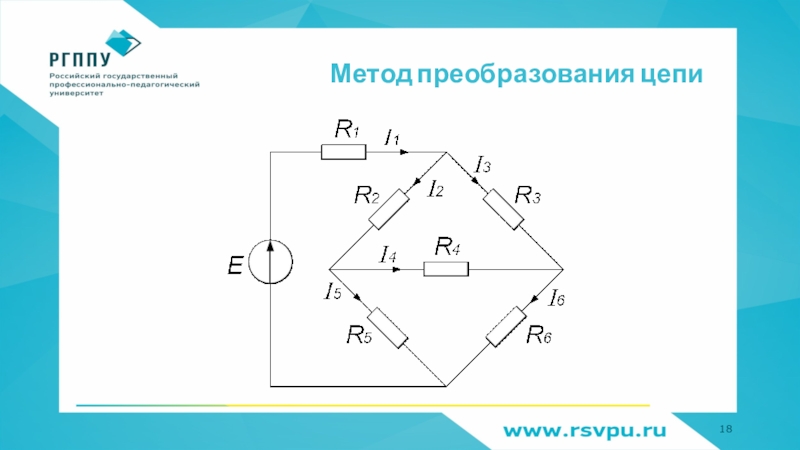
- 18. Метод преобразования цепи
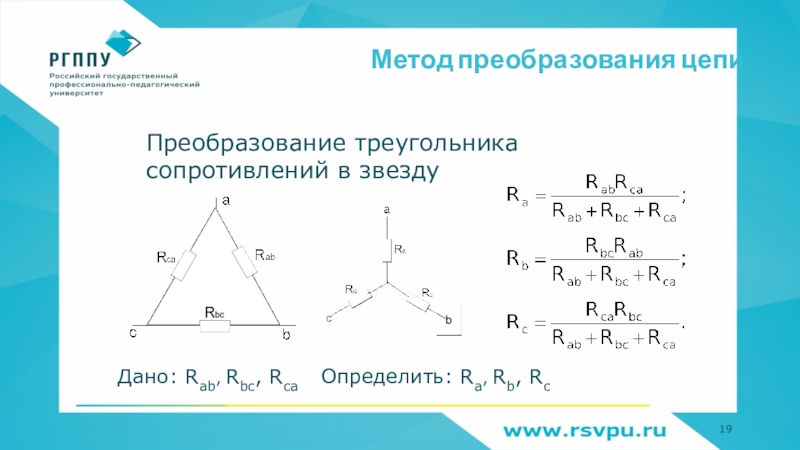
- 19. Метод преобразования цепиПреобразование треугольника сопротивлений в звездуДано: Rab, Rbc, RcaОпределить: Ra, Rb, Rc
- 20. Метод преобразования цепиПреобразование звезды сопротивлений в треугольник Дано: Ra, Rb, RcОпределить: Rab, Rbc, Rca
- 21. Метод непосредственного применения законов КирхгофаОпределить число ветвей
- 22. Метод непосредственного применения законов КирхгофаПроизвольно выбрать условно положительные направления обхода контура.
- 23. Метод непосредственного применения законов КирхгофаСоставить уравнения для
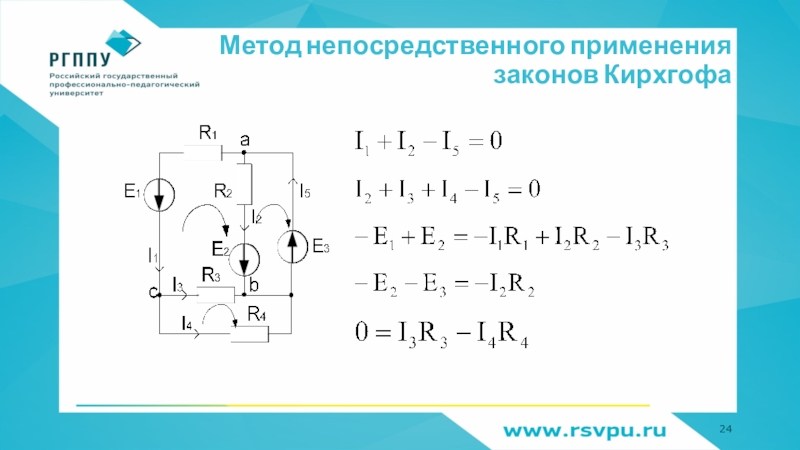
- 24. Метод непосредственного применения законов Кирхгофа
- 25. Метод непосредственного применения законов КирхгофаРешить систему уравнений
- 26. Основные параметры синусоидально изменяющихся величин В линейных
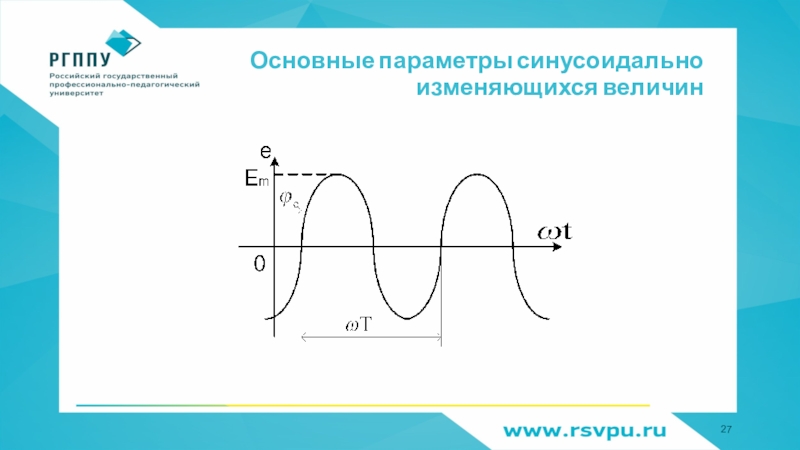
- 27. Основные параметры синусоидально изменяющихся величин
- 28. Um, Im, Em - амплитуда - максимальное
- 29. Основные параметры синусоидально изменяющихся величинначальная фаза, значение
- 30. Основные параметры синусоидально изменяющихся величинf - частота
- 31. Основные параметры синусоидально изменяющихся величинU, I, E
- 32. Основные параметры синусоидально изменяющихся величинФизический смысл действующего
- 33. Основные параметры синусоидально изменяющихся величинДля синусоидального тока:
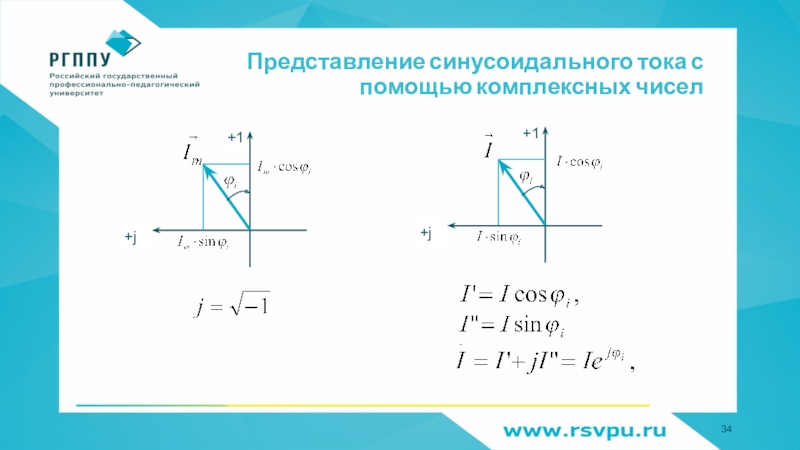
- 34. Представление синусоидального тока с помощью комплексных чисел
- 35. Представление синусоидального тока с помощью комплексных чиселДано:Определить:
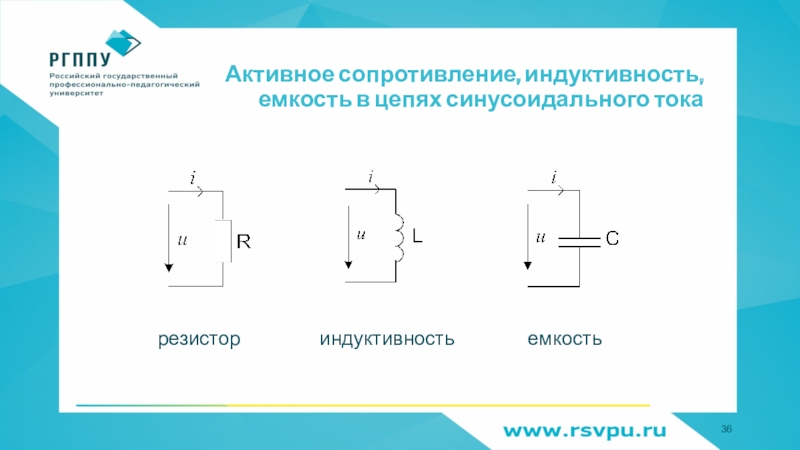
- 36. Активное сопротивление, индуктивность, емкость в цепях синусоидального тока
- 37. Цепь с резисторомДано:Определить:Закон Ома для цепи с резистором
- 38. Цепь с резистором действующие значениязакон Ома для действующих значений напряжения и тока на резисторе
- 39. Цепь с резистором В комплексной форме:закон Ома в комплексной форме для цепи с активным сопротивлением
- 40. Цепь с индуктивностьюДано:Определить: По закону электромагнитной индукции
- 41. Цепь с индуктивностьют.к. в линейных электрических цепях синусоидального тока ток и напряжение изменяются по синусоидальному закону
- 42. Цепь с индуктивностьюиндуктивное сопротивление Ток на участке
- 43. Цепь с индуктивностью В комплексной форме:закон Ома в комплексной форме для цепи с индуктивным сопротивлением
- 44. Цепь с емкостьюДано:Определить:Электрический ток, протекающий через конденсатор, есть скорость изменения заряда на его обкладках:
- 45. Цепь с емкостью
- 46. Цепь с емкостьюемкостное сопротивление
- 47. Цепь с емкостьюзакон Ома для действующих значений
- 48. Цепь с емкостью - закон Ома в комплексной форме
- 49. Последовательное соединение активного, индуктивного, емкостного сопротивленийДано:Определить:
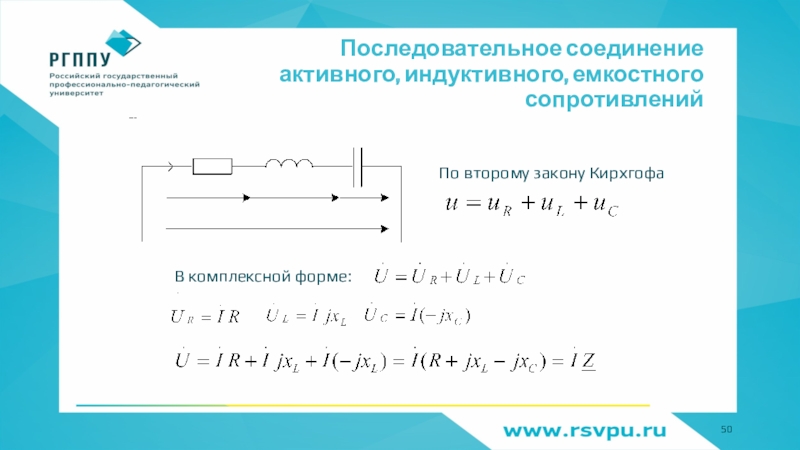
- 50. Последовательное соединение активного, индуктивного, емкостного сопротивленийПо второму закону КирхгофаВ комплексной форме:
- 51. Последовательное соединение активного, индуктивного, емкостного сопротивленийкомплексное сопротивление цепигде х=хL –xC – реактивное сопротивление цепи
- 52. Последовательное соединение активного, индуктивного, емкостного сопротивленийКомплексное сопротивление в показательной форме
- 53. Последовательное соединение активного, индуктивного, емкостного сопротивленийПусть вектор
- 54. Основные характеристики периодического несинусоидального токаЭДС, напряжения, токи
- 55. Расчет электрической цепи с несинусоидальными ЭДС и
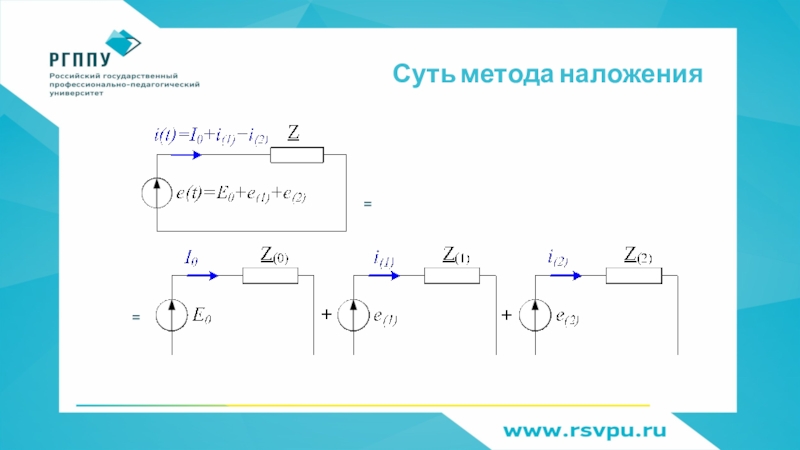
- 56. Суть метода наложения=
- 57. Суть метода наложения==
- 58. Трехфазные электрические цепи. Мгновенные значения и комплексы действующих значений ЭДС
- 59. Мгновенные значения и комплексы действующих значений ЭДС
- 60. Векторная диаграмма ЭДС трехфазного генератора
- 61. Обозначения на схемахначала фаз -первыми буквами латинского
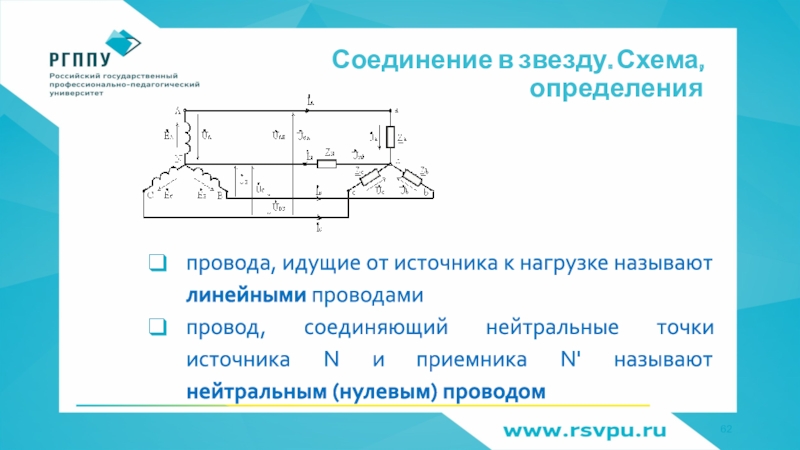
- 62. Соединение в звезду. Схема, определенияпровода, идущие от
- 63. Соединение в звезду. Схема, определенияНапряжения между началами
- 64. Соединение в звезду. Схема, определенияНапряжения между началом
- 65. Соединение в звезду. Схема, определениятоки в фазах
- 66. Соединение генератора с нагрузкойТрехфазный генератор соединяется с
- 67. Соединение в звезду. Фазные и линейные напряжения
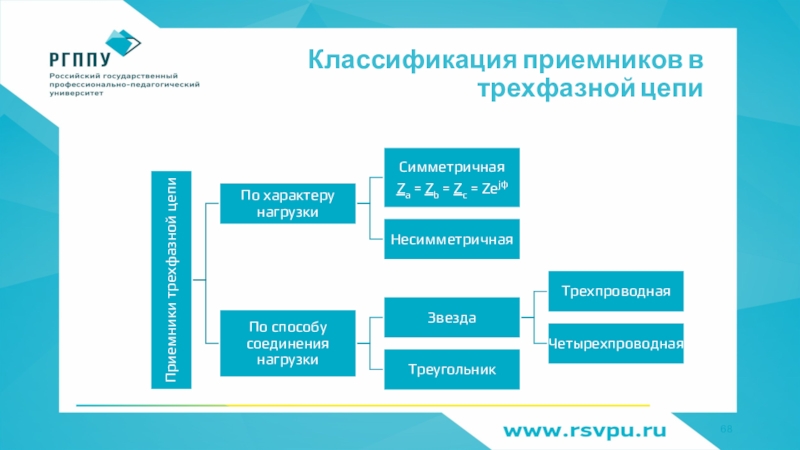
- 68. Классификация приемников в трехфазной цепи
- 69. Четырехпроводная звезда (звезда с нейтральным проводом)İa = Úa / Za; İb = Úb / Zb; İc = Úc / ZcİN = İa + İb + İc
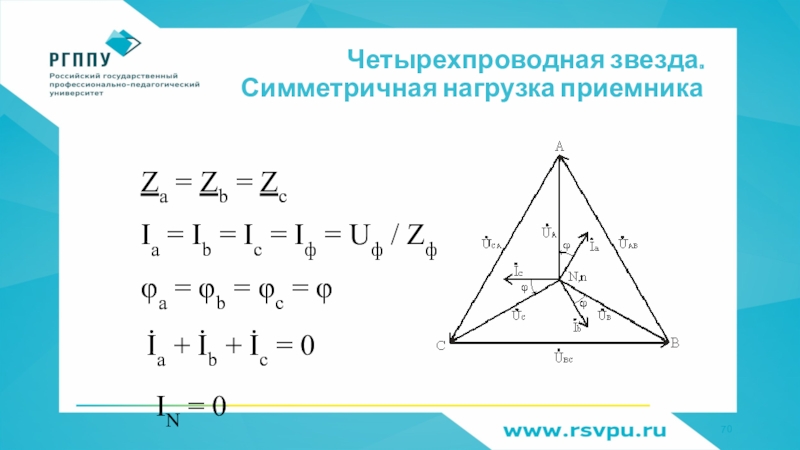
- 70. Четырехпроводная звезда. Симметричная нагрузка приемникаZa = Zb = ZcIa = Ib = Ic = Iф = Uф / Zфφa = φb = φc = φİa + İb + İc = 0IN = 0
- 71. Четырехпроводная звезда. Несимметричная нагрузка приемникаZa ≠ Zb ≠ Zc φa ≠ φb ≠ φc İa = Úa / Za; İb = Úb / Zb; İc = Úc / ZсİN = İa + İb + İc
- 72. Четырехпроводная звезда. Несимметричная нагрузка приемникаНейтральный провод обеспечивает
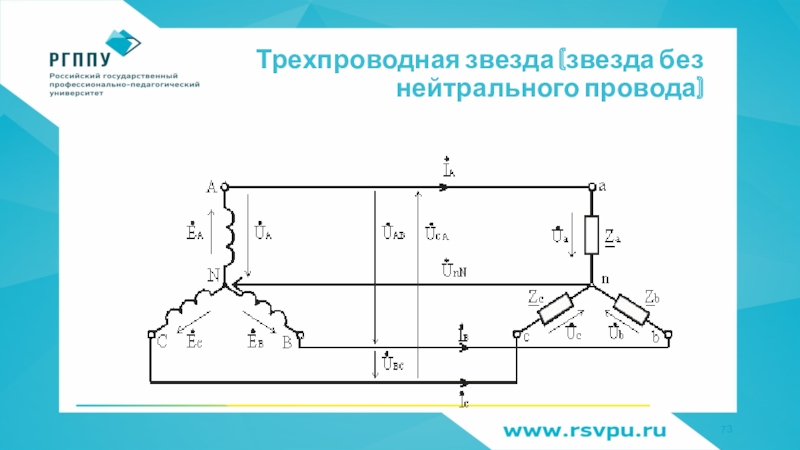
- 73. Трехпроводная звезда (звезда без нейтрального провода)
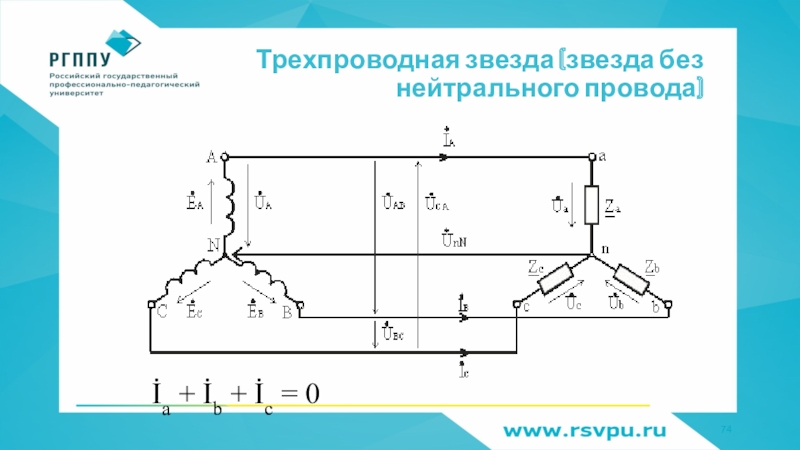
- 74. Трехпроводная звезда (звезда без нейтрального провода)İa + İb + İc = 0
- 75. Трехпроводная звезда. Симметричная нагрузкаZa = Zb = ZcIa = Ib = Ic = Iф = Uф / Zфφa = φb = φc = φİa + İb + İc = 0 нейтрального провода нет
- 76. Трехпроводная звезда. Симметричная нагрузка
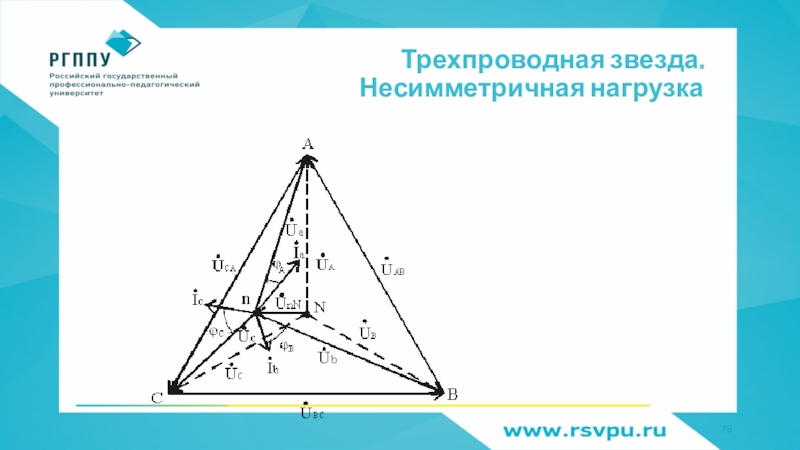
- 77. Трехпроводная звезда. Несимметричная нагрузкаZa ≠ Zb ≠ Zc φa ≠ φb ≠ φc напряжение смещения нейтралиYa = 1 / Za; Yb = 1 / Zb; Yc = 1 / Zc комплексы проводимостей фаз
- 78. Трехпроводная звезда. Несимметричная нагрузкаÚa = ÚA - ÚnN; Úb =
- 79. Трехпроводная звезда. Несимметричная нагрузка
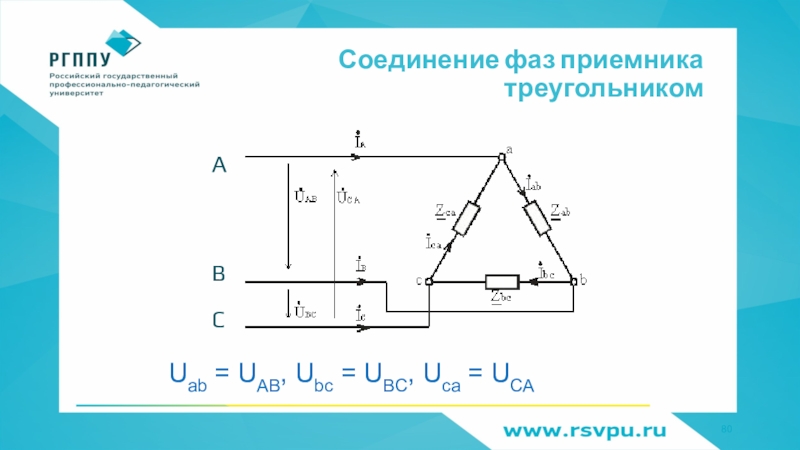
- 80. Соединение фаз приемника треугольникомUab = UAB, Ubc = UBC, Uca = UCAABC
- 81. Соединение фаз генератора и приемника треугольникомİab, İbc ,
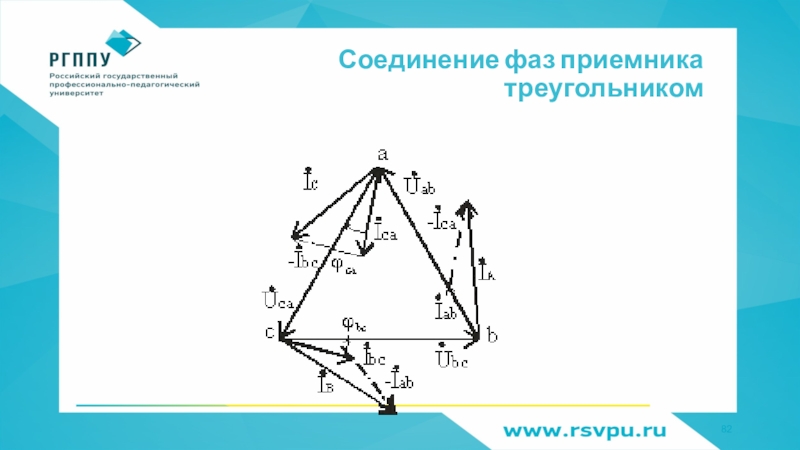
- 82. Соединение фаз приемника треугольником
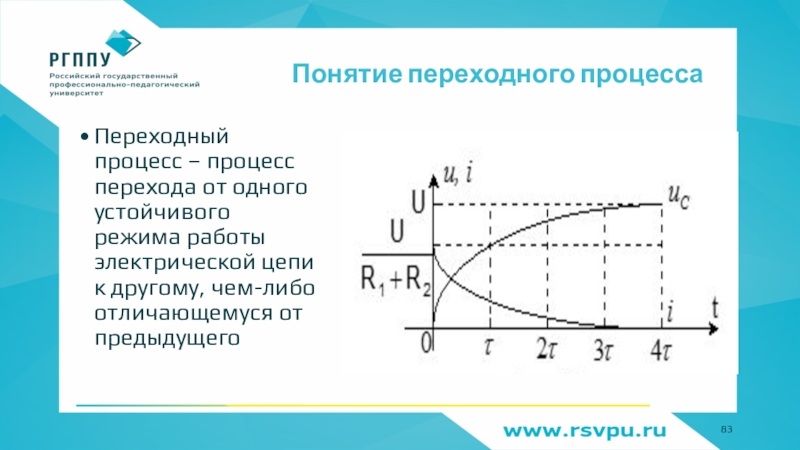
- 83. Понятие переходного процессаПереходный процесс – процесс перехода
- 84. Понятие переходного процессаВозникает вследствие коммутации:включения или отключения
- 85. Понятие переходного процессаКоммутация в переходных процессах —
- 86. Понятие переходного процессаНачало отсчета времени переходного процесса
- 87. Понятие переходного процессаЦель расчета – в определении законов изменения токов и напряжений во время коммутации
- 88. Законы коммутации. Первый закон коммутацииТок через
- 89. Законы коммутации. Второй закон коммутацииНапряжение на
- 90. Независимые и зависимые начальные условияНачальные условия –
- 91. Независимые и зависимые начальные условияНезависимые начальные условия
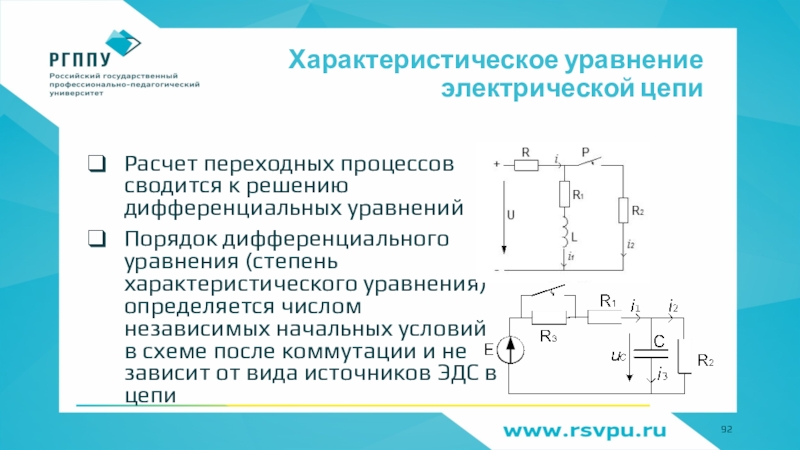
- 92. Характеристическое уравнение электрической цепиРасчет переходных процессов сводится
- 93. Спасибо за внимание!
- 94. Скачать презентанцию
ОбщееТрудоемкость дисциплины: 6 з.е. (216 часов)Аудиторные занятия (16 часов):лекции 4 часа практические занятия 6 часалабораторные работы 6 часовсамостоятельная работа 216-16=200 часовКонтрольная работа (8 задач)Экзамен
Слайды и текст этой презентации
Слайд 1Теоретические основы электротехники
Прокубовская Алла Олеговна, руководитель образовательных проектов Института инженерно-педагогического
образования, зав. кафедрой энергетики и транспорта
Слайд 2Общее
Трудоемкость дисциплины: 6 з.е. (216 часов)
Аудиторные занятия (16 часов):
лекции 4
часа
практические занятия 6 часа
лабораторные работы 6 часов
самостоятельная работа 216-16=200
часовКонтрольная работа (8 задач)
Экзамен
Слайд 3Контрольная работа
Расчет электрических цепей постоянного тока.
Расчет однофазных электрических цепей синусоидального
тока.
Расчет однофазных электрических цепей периодического несинусоидального тока.
Расчет трехфазных цепей синусоидального
тока при соединении нагрузки четырехпроводной звездой.Расчет трехфазных цепей синусоидального тока при соединении нагрузки трехпроводной звездой.
Расчет трехфазных цепей синусоидального тока при соединении нагрузки треугольником.
Расчет переходных процессов в цепях постоянного тока, содержащих емкость.
Расчет переходных процессов в цепях постоянного тока, содержащих индуктивность.
Слайд 4Требования к предъявлению контрольной работы
Выполняется свой вариант в каждом задании.
Количество заданий в каждой задаче разное, поэтому надо определить свой
вариант каждой задачиЗадания представляются в формате MS Word, расчеты – в формате MS Excel
Все векторные диаграммы строятся в масштабе с указанием масштаба по току и по напряжению
В ТаймЛайн задачи размещаются по одной, каждая в свою отдельную ячейку
Преподаватель имеет право попросить обучающегося объяснить решение той или иной задачи
Слайд 5Определение варианта задач контрольной работы
Номер варианта - остаток от деления
двух последних цифр номера зачетной книжки (студенческого билета) на количество
вариантов в данном задании
Слайд 6Определение варианта задач контрольной работы
Номер варианта - остаток от деления
двух последних цифр номера зачетной книжки (студенческого билета) на количество
вариантов в данном задании
Слайд 7Определение варианта задач контрольной работы
Номер варианта - остаток от деления
двух последних цифр номера зачетной книжки (студенческого билета) на количество
вариантов в данном задании
Слайд 9Основные законы электрических цепей постоянного тока
Закон Ома
для участка цепи
без источника ЭДС
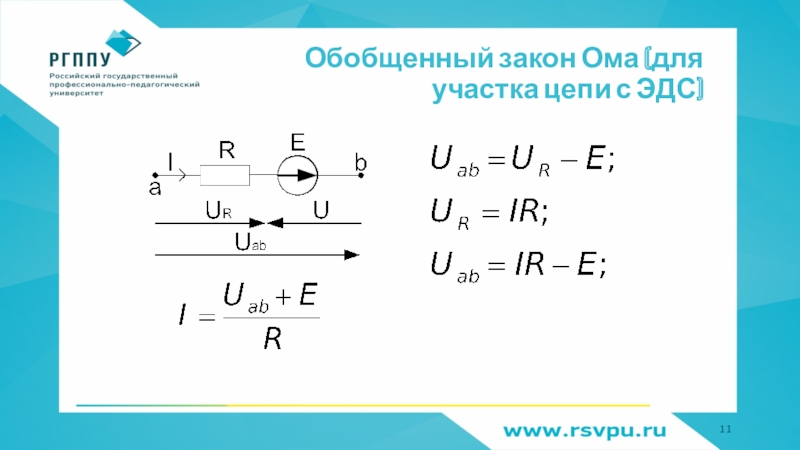
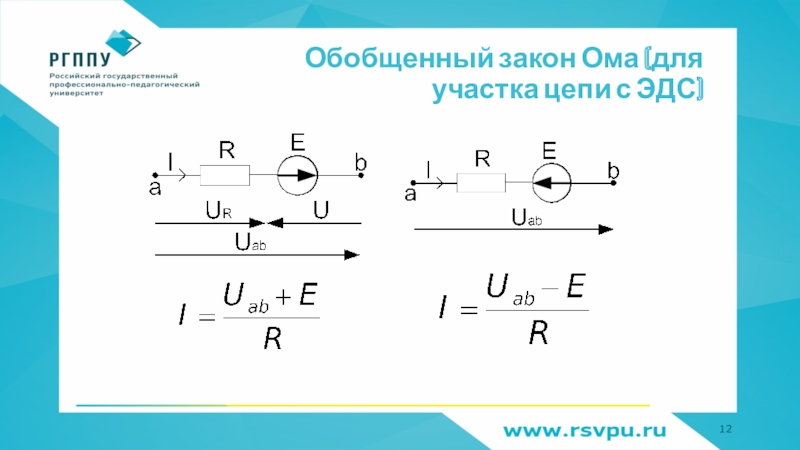
обобщенный закон Ома (для участка цепи с ЭДС)
I закон Кирхгофа
II закон Кирхгофа
Слайд 10Закон Ома для участка цепи без источника
Сила тока на
участке электрической цепи прямо пропорциональна напряжению на концах этого участка
и обратно пропорциональна сопротивлению этого участка
Слайд 13I закон Кирхгофа
Алгебраическая сумма токов в узле электрической цепи равна
нулю.
Для узла а:
Токи, одинаково направленные относительно узла, записываются
с одинаковым знаком 
Слайд 14II закон Кирхгофа
Алгебраическая сумма падений напряжений любого контура равна алгебраической
сумме ЭДС этого контура
Падения напряжения: знак «+», если направления
тока совпадает с направлением обхода контура; ЭДС: знак «+», если направления ЭДС и обхода контура совпадают
Слайд 16Метод преобразования цепи
Последовательное соединение резисторов
Ток во всех последовательно соединенных
элементах одинаков
Слайд 19Метод преобразования цепи
Преобразование треугольника сопротивлений в звезду
Дано: Rab, Rbc, Rca
Определить:
Ra, Rb, Rc
Слайд 20Метод преобразования цепи
Преобразование звезды сопротивлений в треугольник
Дано: Ra, Rb,
Rc
Определить: Rab, Rbc, Rca
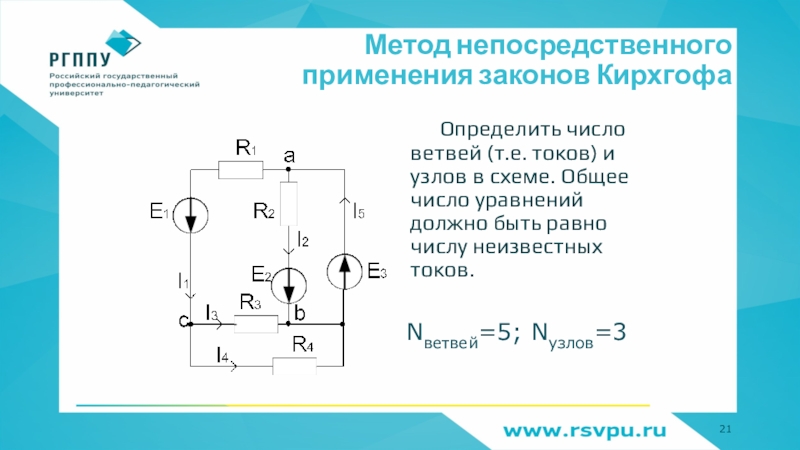
Слайд 21Метод непосредственного применения законов Кирхгофа
Определить число ветвей (т.е. токов) и
узлов в схеме. Общее число уравнений должно быть равно числу
неизвестных токов.Nветвей=5; Nузлов=3
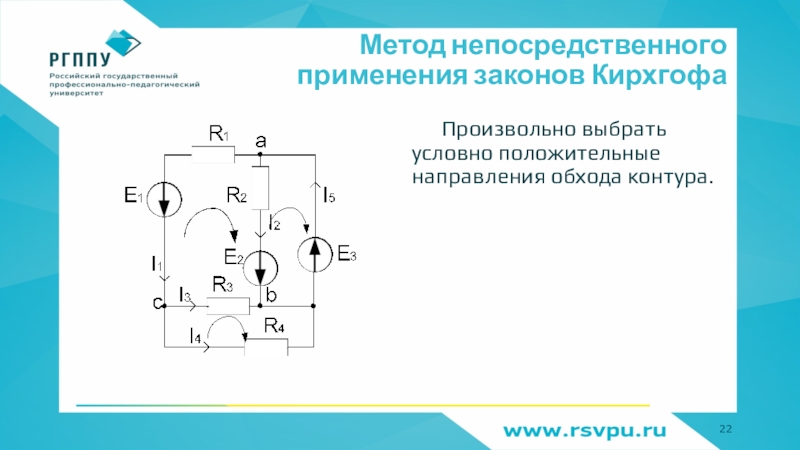
Слайд 22Метод непосредственного применения законов Кирхгофа
Произвольно выбрать условно положительные направления обхода
контура.
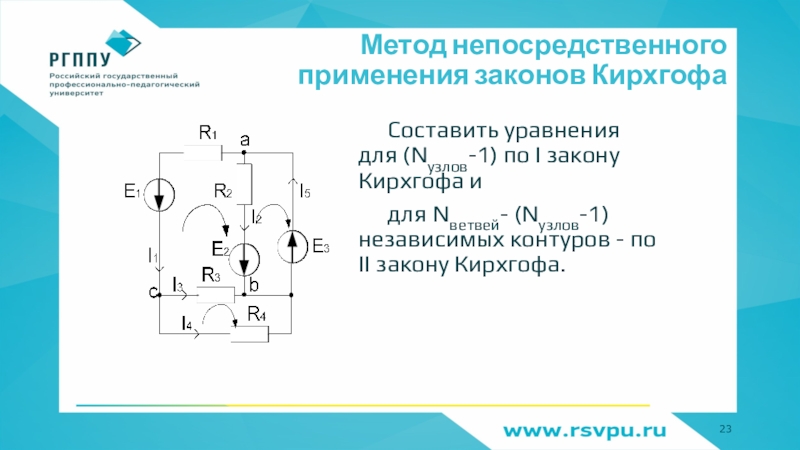
Слайд 23Метод непосредственного применения законов Кирхгофа
Составить уравнения для (Nузлов-1) по I
закону Кирхгофа и
для Nветвей- (Nузлов-1) независимых контуров - по
II закону Кирхгофа. 
Слайд 25Метод непосредственного применения законов Кирхгофа
Решить систему уравнений относительно токов. Если
в результате ток получился отрицательным, то его действительное направление противоположно
выбранному.Проверить правильность решения задачи, составив уравнение баланса мощности.
Слайд 26Основные параметры синусоидально изменяющихся величин
В линейных цепях синусоидального тока
напряжение, ЭДС, ток изменяются по синусоидальному закону:
Слайд 28Um, Im, Em - амплитуда - максимальное значение синусоидальной величины;
Основные параметры синусоидально изменяющихся величин
u, i, e -
мгновенные значения напряжения, тока, ЭДС (значения в данный момент времени);фаза (фазовый угол);
- угловая частота (с-1)
Слайд 29Основные параметры синусоидально изменяющихся величин
начальная фаза, значение аргумента в начальный
момент времени;
Т - период - наименьший интервал времени, через который
мгновенные значения величины повторяются; 
Слайд 30Основные параметры синусоидально изменяющихся величин
f - частота (Гц) – число
периодов в секунду
- сдвиг фаз между напряжением и
током 
Слайд 31Основные параметры синусоидально изменяющихся величин
U, I, E - действующее значение
(тепловой эквивалент постоянному току):
;
;
Слайд 32Основные параметры синусоидально изменяющихся величин
Физический смысл действующего значения переменного тока:
это такой постоянный ток, который за то же время, проходя
через то же сопротивление, выделяет такое же количество тепла, что и данный переменный ток.
Слайд 38Цепь с резистором
действующие значения
закон Ома для действующих значений напряжения
и тока на резисторе
Слайд 39Цепь с резистором
В комплексной форме:
закон Ома в комплексной форме
для цепи с активным сопротивлением
Слайд 41Цепь с индуктивностью
т.к. в линейных электрических цепях синусоидального тока ток
и напряжение изменяются по синусоидальному закону
Слайд 42Цепь с индуктивностью
индуктивное сопротивление
Ток на участке цепи синусоидального
тока, содержащем индуктивность, отстает от напряжения на угол 90о
Слайд 43Цепь с индуктивностью
В комплексной форме:
закон Ома в комплексной форме
для цепи с индуктивным сопротивлением
Слайд 44Цепь с емкостью
Дано:
Определить:
Электрический ток, протекающий через конденсатор, есть скорость изменения
заряда на его обкладках:
Слайд 47Цепь с емкостью
закон Ома для действующих значений тока и напряжения
на участке цепи, содержащем емкость.
ток на емкости опережает напряжение на
угол 90°, или напряжение отстает от тока на угол 90°
Слайд 49Последовательное соединение активного, индуктивного, емкостного сопротивлений
Дано:
Определить:
Слайд 50Последовательное соединение активного, индуктивного, емкостного сопротивлений
По второму закону Кирхгофа
В комплексной
форме:
Слайд 51Последовательное соединение активного, индуктивного, емкостного сопротивлений
комплексное сопротивление цепи
где х=хL –xC
– реактивное сопротивление цепи
Слайд 52Последовательное соединение активного, индуктивного, емкостного сопротивлений
Комплексное сопротивление в показательной форме
Слайд 53Последовательное соединение активного, индуктивного, емкостного сопротивлений
Пусть вектор тока совпадает с
положительным направлением оси действительных чисел
Вектор падения напряжения на резисторе совпадает
по направлению с вектором тока, протекающего через него.Вектор падения напряжения на индуктивности опережает вектор тока, протекающего через него, на угол 90°
Вектор падения напряжения на емкости отстает от вектора тока, протекающего через него, на угол 90°
Слайд 54Основные характеристики периодического несинусоидального тока
ЭДС, напряжения, токи удовлетворяют условиям Дирихле,
поэтому их можно представить в виде ряда Фурье (гармонического ряда):
Слайд 55Расчет электрической цепи с несинусоидальными ЭДС и токами
Суть метода: линейная
электрическая цепь для каждой гармонической составляющей ЭДС независима.
Расчет выполняется
методом наложения
Слайд 61Обозначения на схемах
начала фаз -первыми буквами латинского алфавита ( А, В,
С ),
концы фаз - последними буквами ( X, Y, Z ),
направления
ЭДС указывают от конца фазы обмотки генератора к ее началу. 
Слайд 62Соединение в звезду. Схема, определения
провода, идущие от источника к нагрузке
называют линейными проводами
провод, соединяющий нейтральные точки источника N и
приемника N' называют нейтральным (нулевым) проводом 
Слайд 63Соединение в звезду. Схема, определения
Напряжения между началами фаз или между
линейными проводами называют линейными напряжениями (UAB, UBC, UCA)
Слайд 64Соединение в звезду. Схема, определения
Напряжения между началом и концом фазы
или между линейным и нейтральным проводами называются фазными напряжениями (UA, UB, UC у
источника; Ua, Ub, Uc у приемника).
Слайд 65Соединение в звезду. Схема, определения
токи в фазах приемника или источника
называют фазными токами,
токи в линейных проводах называются линейными токами
Слайд 66Соединение генератора с нагрузкой
Трехфазный генератор соединяется с нагрузкой четырьмя линейными
проводами либо тремя.
Общие точки генератора О и потребителя О'
называют нулевыми (нейтральными).Провод 00' — нулевой (О) или нейтральный (N) провод.
Слайд 69Четырехпроводная звезда (звезда с нейтральным проводом)
İa = Úa / Za;
İb = Úb / Zb;
İc =
Úc / Zc
İN = İa + İb + İc
Слайд 70Четырехпроводная звезда. Симметричная нагрузка приемника
Za = Zb = Zc
Ia = Ib = Ic = Iф = Uф / Zф
φa =
φb = φc = φ
İa + İb + İc = 0
IN = 0
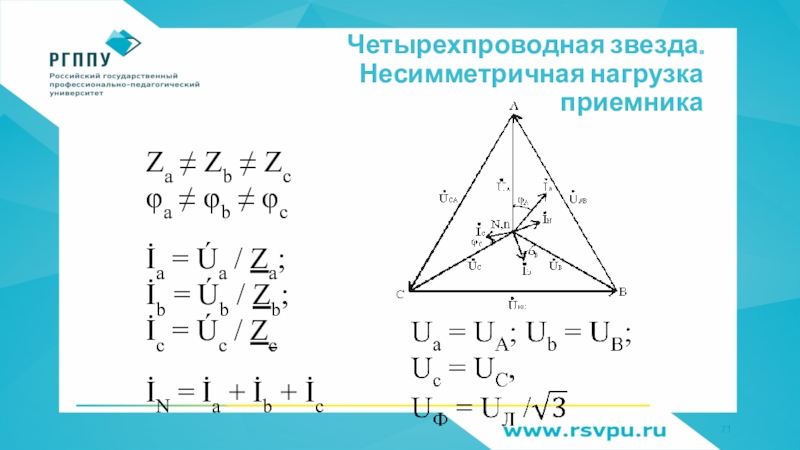
Слайд 71Четырехпроводная звезда. Несимметричная нагрузка приемника
Za ≠ Zb ≠ Zc
φa ≠ φb ≠ φc
İa = Úa / Za;
İb = Úb / Zb;
İc = Úc / Zс
İN =
İa + İb + İc
Слайд 72Четырехпроводная звезда. Несимметричная нагрузка приемника
Нейтральный провод обеспечивает симметрию фазных напряжений
приемника при несимметричной нагрузке
Режим работы каждой фазы нагрузки, находящейся под
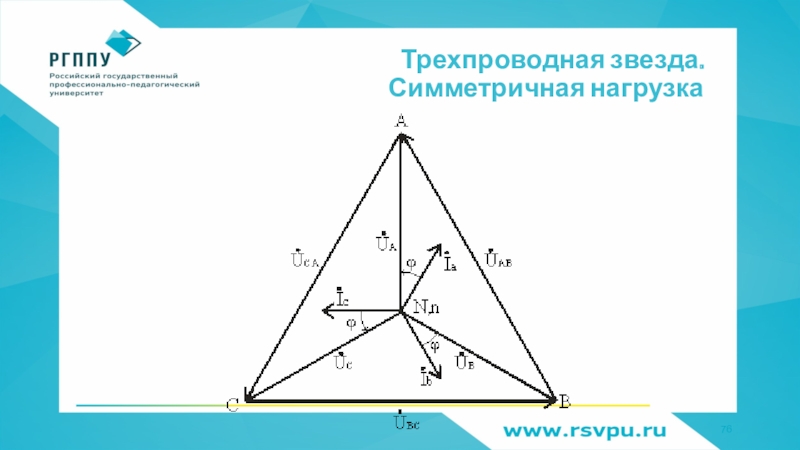
неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз
Слайд 75Трехпроводная звезда. Симметричная нагрузка
Za = Zb = Zc
Ia = Ib = Ic = Iф = Uф / Zф
φa = φb =
φc = φ
İa + İb + İc = 0
нейтрального провода нет
Слайд 77Трехпроводная звезда. Несимметричная нагрузка
Za ≠ Zb ≠ Zc
φa ≠ φb ≠ φc
напряжение смещения нейтрали
Ya = 1 / Za;
Yb = 1 / Zb;
Yc =
1 / Zc
комплексы проводимостей фаз
Слайд 78Трехпроводная звезда. Несимметричная нагрузка
Úa = ÚA - ÚnN;
Úb = ÚB - ÚnN;
Úc =
ÚC - ÚnN
По второму закону Кирхгофа
По закону Ома
İa = Úa / Za = Ya Úa;
İb = Úb / Zb = Yb Úb;
İc = Úc / Zc = Yc Úc
Слайд 81Соединение фаз генератора и приемника треугольником
İab, İbc , İca
фазные токи
İA, İB ,
İC
линейные токи
İA = İab - İca;
İB = İbc - İab;
İC = İca - İbc
İA +
İB + İC = 0
Слайд 83Понятие переходного процесса
Переходный процесс – процесс перехода от одного устойчивого
режима работы электрической цепи к другому, чем-либо отличающемуся от предыдущего
Слайд 84Понятие переходного процесса
Возникает вследствие коммутации:
включения или отключения пассивных или активных
ветвей,
коротких замыканий отдельных участков,
различного рода переключений,
внезапного изменения
параметров и т.д.Заканчивается спустя некоторое время после коммутации
Слайд 85Понятие переходного процесса
Коммутация в переходных процессах — мгновенное изменение параметров
электрической цепи
Коммутация — процессы, происходящие в первый момент времени после
переключения в электрических цепях при замыканиях и размыканиях различных участков цепи
Слайд 86Понятие переходного процесса
Начало отсчета времени переходного процесса t=0 начинается с
момента коммутации
Момент времени непосредственно перед коммутацией t=0-
Момент времени сразу
после коммутации - t=0+
Слайд 87Понятие переходного процесса
Цель расчета – в определении законов изменения токов
и напряжений во время коммутации
Слайд 88Законы коммутации.
Первый закон коммутации
Ток через индуктивность непосредственно до коммутации
равен току через ту же индуктивность непосредственно после коммутации
Ток
на индуктивности не может изменяться скачком
Слайд 89Законы коммутации.
Второй закон коммутации
Напряжение на емкости непосредственно до коммутации
равно напряжению на той же емкости непосредственно после коммутации,
Напряжение
на емкости не может измениться скачком
Слайд 90Независимые и зависимые начальные условия
Начальные условия – значения токов и
напряжений в первый момент после коммутации t=0+
Слайд 91Независимые и зависимые начальные условия
Независимые начальные условия определяются из законов
коммутации:
Зависимые начальные условия определяются из законов Кирхгофа и известных независимых
начальных условий
Слайд 92Характеристическое уравнение электрической цепи
Расчет переходных процессов сводится к решению дифференциальных
уравнений
Порядок дифференциального уравнения (степень характеристического уравнения) определяется числом независимых начальных
условий в схеме после коммутации и не зависит от вида источников ЭДС в цепи
