Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория чисел
Содержание
- 1. Теория чисел
- 2. План:Вопрос 1. История становления теории чисел.Вопрос 2.
- 3. Вопрос 1. История становления теории чисел
- 4. Теория чисел - этоветвь математики, имеющая дело
- 5. Археология и история учат нас, что человек
- 6. НумерологияНекоторые следы размышлений о числах в давние
- 7. Примером ранней теории чисел может служить теорема
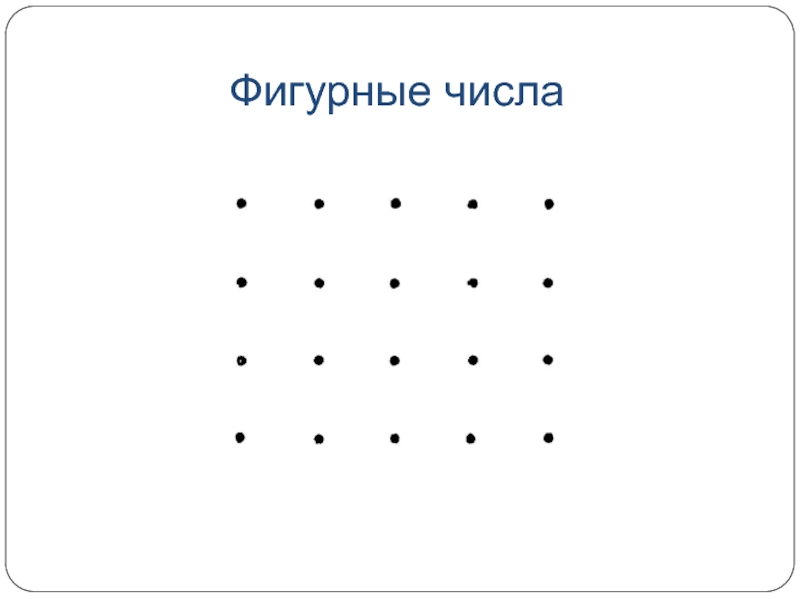
- 8. Фигурные числаВ теории чисел мы часто встречаемся
- 9. Фигурные числаГреки предпочитали думать о числах, как
- 10. Фигурные числа
- 11. Фигурные числаЛюбое целое число, которое является произведением
- 12. Фигурные числаТакие числа греки называли простыми числами.
- 13. Магические квадратымагическим квадратом является расположение чисел от
- 14. Вопрос 2. Простые и составные числа
- 15. Одним из первых свойств чисел, открытых человеком,
- 16. Простые и составные числаЛюбое число с >
- 17. Простые числа среди первой тысячи чисел
- 18. ЗадачиКакие из следующих чисел являются простыми: а)
- 19. Вопрос 3. Делители чисел
- 20. Основная теорема о разложении на множителиЛюбое
- 21. Основная теорема о разложении на множителиНезависимо
- 22. Вопрос 4. Системы счисления
- 23. Система счисления — это совокупность правил наименования
- 24. Людьми использовались различные способы записи чисел, которые можно объединить в несколько групп:унарная;непозиционная;позиционная.
- 25. Унарная система Система счисления, в которой для
- 26. Непозиционная система счисления — система счисления, в
- 27. Двоичная система счисления0 – ноль1 – один
- 28. Восьмеричная система счисления000 – ноль001 – один010
- 29. Из непозиционных наиболее распространенной можно считать римскую
- 30. Основание системы счисления – это количество знаков,
- 31. Скачать презентанцию
План:Вопрос 1. История становления теории чисел.Вопрос 2. Простые и составные числа.Вопрос 3. Делители чисел.Вопрос 4. Системы счисления.
Слайды и текст этой презентации
Слайд 4Теория чисел - это
ветвь математики, имеющая дело с целыми положительными
числами (1, 2, 3…, n), которые также называют натуральными числами
.Слайд 5Археология и история учат нас, что человек рано начал считать.
Сначала он научился складывать числа, потом, много позже, умножать и
вычитать их. Деление чисел было необходимым для распределения на равные части кучи яблок или улова рыбы. Эти действия над числами называются вычислениями. В некоторых случаях последовательность вычислений называют «калькуляцией». Это слово происходит от латинского «calculus», означающего «маленький камень», поскольку римляне пользовались морской галькой при вычислениях на своих счетных досках.Слайд 6Нумерология
Некоторые следы размышлений о числах в давние времена можно обнаружить
в суеверных предрассудках, связанных с числами.
Среди чисел есть «счастливые»,
которым нужно отдавать предпочтение и радоваться при встрече с ними, и «несчастливые», которых нужно остерегаться, как дурного глаза. Например, из нумерологии в античной Греции, нечетные числа, большие единицы, символизировали мужское начало, а четные — женское; таким образом, число 5 — сумма первого мужского и первого женского чисел — символизировало супружество или союз.
Слайд 7Примером ранней теории чисел может служить теорема Пифагора
В прямоугольном
треугольнике длины сторон удовлетворяют соотношению Пифагора: с2 = а2 +
b2, где с – длина гипотенузы.Это дает возможность в прямоугольном треугольнике вычислить длину одной стороны, если известны две другие.
Не совсем справедлива эту теорему назвали в честь греческого философа Пифагора, она была известна вавилонянам почти за 2000 лет до Пифагора.
Слайд 8Фигурные числа
В теории чисел мы часто встречаемся с квадратами, т.
е. такими числами, как:
32 = 9, 72 = 49, 102
= 100,и аналогично с кубами, т. е. такими числами, как:
23 = 8, 33 = 27, 53 = 125.
Слайд 9Фигурные числа
Греки предпочитали думать о числах, как о геометрических величинах:
произведение с = а*b рассматривалось как площадь с прямоугольника со
сторонами a и b. Также можно было рассматривать a*b как число точек в прямоугольной таблице с а точками на одной стороне и b точками на другой. Например, 20 = 4*5 есть число точек в прямоугольной таблице..Слайд 11Фигурные числа
Любое целое число, которое является произведением двух целых чисел,
можно было назвать прямоугольным числом. Когда две стороны прямоугольника имеют
одну и ту же длину, то такое число является квадратным числом, или квадратом.Некоторые числа нельзя представлять в виде прямоугольных чисел иначе, как тривиальным способом — в виде цепочки точек, лежащих в одном ряду.
Например, пять может быть представлено как прямоугольное число лишь единственным способом, взяв одну сторону равной единице, а другую — пяти. Поэтому число 5 представлялось в виде цепочки точек, лежащих в одном ряду: . . . . .
Слайд 12Фигурные числа
Такие числа греки называли простыми числами.
Точка, взятая в
одном экземпляре, не рассматривалась как число.
Число 1 явилось тем
кирпичом, из которого строились все остальные числа. Таким образом, 1 не была для них и не считается сейчас простым числом.
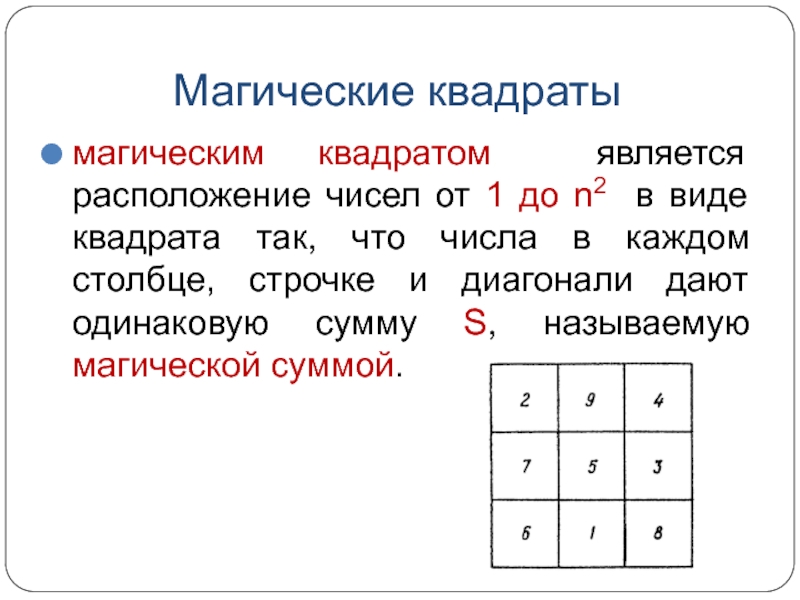
Слайд 13Магические квадраты
магическим квадратом является расположение чисел от 1 до n2
в виде квадрата так, что числа в каждом столбце, строчке
и диагонали дают одинаковую сумму S, называемую магической суммой.Слайд 15Одним из первых свойств чисел, открытых человеком, было то, что
некоторые из них могут быть разложены на два или более
множителя, например,6 = 2*3, 9 = 3*3, 30 = 2*15 = 3*10,
в то время как другие, например, 3, 7, 13, 37, не могут быть разложены на множители подобным образом.
Когда число c = a*b является произведением двух чисел a и b, то мы называем а и b множителями или делителями числа с .
Каждое число имеет тривиальное разложение на множители с = 1*с = с *1.
Соответственно числа 1 и с называются тривиальными делителями числа с .
Слайд 16Простые и составные числа
Любое число с > 1, у которого
существует нетривиальное разложение на множители, называется составным.
Если число с
имеет только тривиальное разложение на множители, то оно называется простым. Среди первых 100 чисел простыми являются следующие 25 чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Все остальные числа, кроме 1, являются составными.
Можем сформулировать следующее утверждение:
Любое целое число с > 1 является, либо простым, либо имеет простой множитель.
Слайд 18Задачи
Какие из следующих чисел являются простыми:
а) год вашего рождения;
б) текущий год;
в) номер вашего дома.
Найдите простое число, следующее
за простым числом 1973.Заметим, что числа от 90 до 96 включительно являются семью последовательными составными числами; найдите девять последовательных составных чисел.
Слайд 20Основная теорема о разложении
на множители
Любое составное число с может
быть записано в виде произведения с = a*b, причем ни
один из делителей не равен 1 и каждый из них меньше, чем с ; например, 72 = 8*9, 150 = 10*15.При разложении числа с на множители один из них, и даже оба (а и b ) могут оказаться составными. Если а — составное, то разложение на множители можно продолжить: а = a 1 * a 2, с = a 1 * a 2 * b .
Примерами этого могут служить рассмотренные выше числа
72 = 2 * 4 * 9; 150 = 2 * 5 * 15.
Этот процесс разложения на множители можно продолжить до тех пор, пока он не закончится; это должно произойти, так как делители становятся все меньше и меньше, но не могут стать единицей.
Когда ни один из делителей нельзя уже будет разложить на множители, то все делители будут простыми числами.
Таким образом показали, что каждое целое число, большее 1, является простым числом или произведением простых чисел.
Слайд 21Основная теорема о разложении
на множители
Независимо от способа разложения числа
на простые множители результат всегда будет одним и тем же,
различаясь лишь порядком их записи, т. е. любые два разложения числа на простые множители содержат одни и те же простые числа; при этом каждое простое число содержится одинаковое число раз в обоих разложениях.Этот результат можем кратко выразить следующим образом: разложение числа на простые множители единственно.
Слайд 23Система счисления — это
совокупность правил наименования и записи чисел.
В
любой системе счисления для представления чисел выбираются некоторые символы (цифры,
буквы, черточки и т. д.), которые называются цифрами.Слайд 24Людьми использовались различные способы записи чисел, которые можно объединить в
несколько групп:
унарная;
непозиционная;
позиционная.
Слайд 25Унарная система
Система счисления, в которой для записи чисел используется
только один знак – I («палочка»).
Следующее число получается из предыдущего
добавлением новой I, их количество (сумма) равно самому числу.Именно такая система применяется для начального обучения счету детей («счетные палочки»);
Унарная система важна также в теоретическом отношении, поскольку в ней число представляется наиболее простым способом и, следовательно, просты операции с ним.
Именно унарная система определяет значение целого числа количеством содержащихся в нем единиц, которое не зависит от формы представления.
Слайд 26Непозиционная система счисления — система счисления, в которой значение каждой
цифры не зависит от ее положения в записи числа (римская
система).Позиционная система счисления — система счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр (двоичная, восьмеричная, десятичная).
Слайд 27Двоичная система счисления
0 – ноль
1 – один (и это предел
разряда)
10 – два
11 – три (и это снова предел)
100 –
четыре101 – пять
110 – шесть
111 – семь и т.д.
Слайд 28Восьмеричная система счисления
000 – ноль
001 – один
010 – два
011 –
три
100 – четыре
101 – пять
110 – шесть
111 – семь
Слайд 29Из непозиционных наиболее распространенной можно считать римскую систему счисления. В
ней некоторые базовые числа обозначены заглавными латинскими буквами:
1 – I,
5
– V,10 – X,
50 – L,
100 – C,
500 – D,
1000 – M.
Слайд 30Основание системы счисления – это количество знаков, которое используется для
записи цифр (в десятичной системе основанием является 10).
Разряд - это
позиция цифры в числе. Разрядность числа - количество цифр, из которых состоит число (например, 264 - трехразрядное число, 00010101 - восьмиразрядное число).
Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка - третий).