Слайд 1Теория и технология развития
математических представлений у детей дошкольного возраста
Слайд 2Федеральный государственный образовательный стандарт дошкольного образования от 17 октября 2013
г. N 1155
2.6. Содержание Программы должно обеспечивать развитие личности, мотивации
и способностей детей в различных видах деятельности и охватывать следующие структурные единицы, представляющие определенные направления развития и образования детей (далее - образовательные области):
социально-коммуникативное развитие; познавательное развитие; речевое развитие; художественно-эстетическое развитие; физическое развитие.
Познавательное развитие предполагает развитие интересов детей, любознательности и познавательной мотивации, формирование познавательных действий, развитие воображения и творческой активности; формирование первичных представлений …. об объектах окружающего мира, о свойствах и отношениях объектов окружающего мира (форме, … размере, ….количестве, числе, части и целом, пространстве и времени, движении и покое, причинах и следствиях и др.),
Слайд 3Формирование элементарных математических представлений – это целенаправленный процесс передачи и
усвоения знаний, приемов и способов умственной деятельности, предусмотренных программными требованиями.
Основная его цель – не только подготовка к успешному овладению математикой в школе, но и всестороннее развитие детей.
Формирование элементарных математических представлений дошкольников осуществляется с помощью научно обоснованной методической системы, компонентами которой являются цель, содержание, методы, средства и формы организации работы, теснейшим образом связанных между собой и взаимообусловленных друг другом.
Слайд 4Задачи формирования элементарных математических знаний и последующего математического развития детей:
-приобретение знаний о множестве, числе, величине, форме, пространстве и времени
как основы математического развития;
-формирование широкой начальной ориентации в количественных, пространственных и временных отношениях окружающей действительности;
-формирование навыков и умений в счете, вычислениях, измерении, моделировании, общеучебных умений;
- овладение математической терминологией;
-развитие познавательных интересов и способностей, логического мышления, общее интеллектуальное развитие ребенка.
Слайд 5Современные авторы связывают процесс математического развития ребенка, прежде всего, с
развитием его познавательной сферы, разнообразных способов познания, познавательной деятельностью, а
также развитием математического стиля мышления.
Познавательная деятельность – это активная деятельность ребенка по приобретению и использованию знаний.
Познавательная деятельность характеризуется познавательной активностью ребенка, его активной преобразующей позицией как субъекта этой деятельности, заключающейся:
- в способности видеть и самостоятельно ставить познавательные задачи;
-намечать план действий;
-отбирать способы решения поставленной задачи;
-добиваться результата и анализировать его.
Слайд 6Теоретические основы формирования и развития математических представлений у дошкольников
Основная
цель теоретических основ развития математических представлений — математическое описание и
уточнение смысла всего того, что практикуется на занятиях с дошкольниками, разъяснение тех понятий, о которых у детей формируют соответствующие представления.
Весь процесс формирования элементов математики непосредственно связан с усвоением специальной терминологии. Слово делает понятие осмысленным, подводит к обобщениям, к абстрагированию.
Слайд 7Основные математические понятия
Ключевые слова: множество, число, цифра натуральный ряд
чисел, операции с множествами, объединение множеств, пересечение множеств, вычитание множеств.
Слайд 8Множества и
операции над ними
Слайд 9Множество-основное понятие курса математики.
Суть понятия передается словами «совокупность», «собрание», «набор»
и т.д.
Универсальность понятия- под него можно подвести любую совокупность явлений,
предметов и объектов реального мира.
Примеры множеств-?
В математике приходится рассматривать те или иные группы объектов как единое целое :числа от 1 до 10,натуральные числа, однозначные числа, треугольники, квадраты и т.д.
Все эти совокупности называются множествами.
Слайд 10Обозначение множеств
Множества обозначаются буквами латинского алфавита: А, В, С, …Z.
Как называются объекты, из которых образовано множество?
Элементы множества(обозначают строчными
буквами латинского алфавита: а, в, с,…z.)
{∅}
Объект а принадлежит множеству А
Объект а –элемент множества А
Множество А содержит элемент а
Слайд 12
а А
Объект а не принадлежит множеству А
Объект а не
является элементом множества А
Множество А не содержит элемента а
Слайд 13Пусть А –множество однозначных чисел
Прочтите запись «3 А»
Что
можно сказать о числе 3?
Число 3- однозначное
Прочтите запись «12 А»
Что
можно сказать о числе 12?
Число 12 не является однозначным
Слайд 14A={а, в, с, d, е}
A={а, в, с, d, е …}
Чем
отличаются данные множества?
Конечные и бесконечные множества
Примеры конечных множеств-?
Множество дней недели,
множество детей в конкретной группе, множество букв в алфавите,…
Примеры бесконечных множеств-?
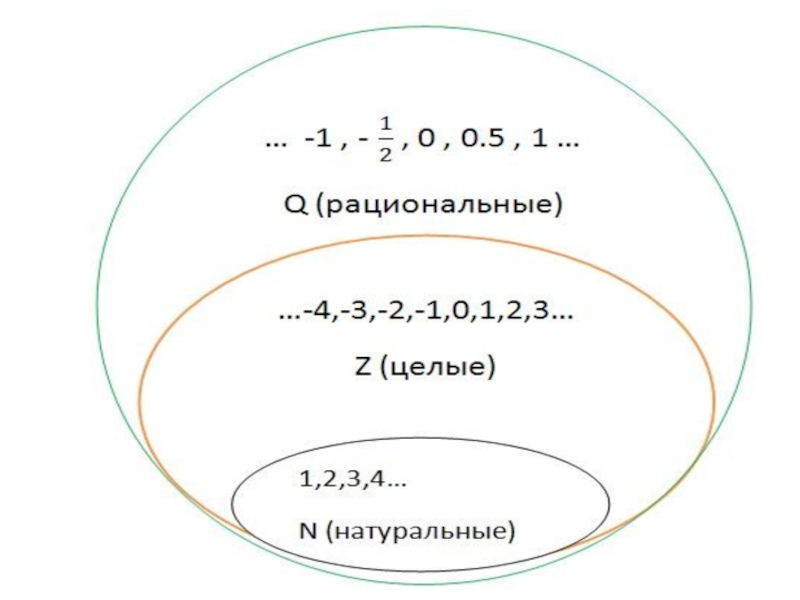
Множество точек на прямой, множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество действительных чисел…
N-?
множество натуральных чисел
Натуральные числа-это…
Натуральные числа — это числа,
используемые для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов.
Натуральные числа, расположенные в порядке возрастания, образуют числовой ряд. Он начинается с наименьшего натурального числа — 1. Наибольшего натурального числа нет, так как ряд натуральных чисел бесконечен
Слайд 16Натуральный ряд чисел обладает следующими свойствами:
Наименьшим натуральным числом
является единица
Единица непосредственно не следует ни за каким
натуральным числом.
Для любого натурального числа существует одно и только одно непосредственно следующее за ним натуральное число.
Любое натуральное число непосредственно следует не более, чем за одним натуральным числом.
Всякое натуральное число, кроме единицы, является «правым» соседом одного и только одного натурального числа, его «левого» соседа.
0 – не является натуральным числом.
Множество натуральных чисел – бесконечное множество
Z-?
Множество целых чисел
Целые числа-это…
Натуральные числа, а
также все числа противоположные им по знаку, и число ноль называют целыми
Q-?
множество рациональных чисел
Рациональные числа -это…
Рациональные числа -
это целые и дробные числа (обыкновенные дроби, конечные десятичные дроби и бесконечные периодические дроби).
π = 3,1415926535897932384626433832795… –это рациональное число
Бесконечные непериодические дроби НЕ входят в множество рациональных чисел. Поэтому число «Пи» , основание натурального логарифма e (e = 2,718..) НЕ являются рациональными числами.
I-?
Множество иррациональных чисел
Множество иррациональных чисел- это…
бесконечные непериодические дроби.
√ 3 = 1,730508075...
число Пи π = 3,14159...
основание натурального логарифма e = 2,71845...
Среди множества чисел иррациональные числа занимают особое место. Они не входят в рациональные числа.
R-?
множество действительных чисел
Действительное число – это
…
Действительное число - это любое положительное число, отрицательное число и нуль.
Действительные числа разделяются на 2 группы:
рациональные и иррациональные.
Слайд 22Задание №1
выпишите истинные высказывания
1) 4 N
2) 60/4 Z
3) -100
R
4) 1 Q
5) 2Q
6) -10/5 N
7) 0
Z
8) 0,089731… I
9) 0 R
10) 1 I
Слайд 23Способы задания множеств
Множество можно задать, перечислив его элементы.
А={3, 4,
5, 6 }
Такой способ используется для задания конечных множеств с
небольшим кол-вом эл-тов; иногда для задания бесконечных мн-в : N ={1, 2, 3 . . . }
Другой способ задания: указывают характеристическое свойство его элементов.
( св-во, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит)
Такой способ задания используется если множество бесконечно или конечное с большим числом элементов
Множество задано, если о любом объекте можно сказать, принадлежит он этому множеству либо не принадлежит.
Слайд 24Характеристическое свойство элементов
Мн-во А – двузначные числа
Характеристическое свойство- ?
Быть двузначным
числом
Характеристическое свойство дает возможность решить вопрос о том, принадлежит какой-либо
объект мн-ву А или не принадлежит
21-? 145-?
Слайд 25Различные характеристические св-ва элементов мн-ва
Мн-во В –мн-во квадратов
Характеристическое св-ва- ?
1-
мн-во прямоугольников с равными сторонами
2-мн-во ромбов с прямыми углами
Слайд 26Задания
№ 2 А-множество двузначных чисел, запись которых оканчивается цифрой1.
Выпишите
числа, которые принадлежат этому множеству 28; 31; 0,21;
61; 147/ 7
Проанализируйте данные множества и устно укажите характеристическое свойство элементов множества:
1) {а, е, ё, и, о, у, э, ю, я, ы}
2) {23, 22, 21, 20, 19, 18, 17, 16, 15}
3) {11, 22, 33, 44, 55, 66, 77, 88, 99}
Множество С состоит из квадрата, треугольника, круга. Принадлежит ли этому множеству диагональ квадрата?
Слайд 27Отношения между множествами
A={а, в, с, d, е}
B={ в, d, k, е}
в,d,е –общие
элементы мн-в А и В-множества А и В пересекаются
A={а, в, с, d, е} В={m, r, z, f, k}
Множества, которые не имеют общих элементов не пересекаются
Слайд 28Отношения между множествами
A={а, в, с, d, е}
B={ с, d, е}
Пересекаются, каждый
эл-т мн-ва В яв-ся эл-том мн-ва А
мн-во В яв-ся подмножеством А
Сформулируйте определение для множества В относительно множества А
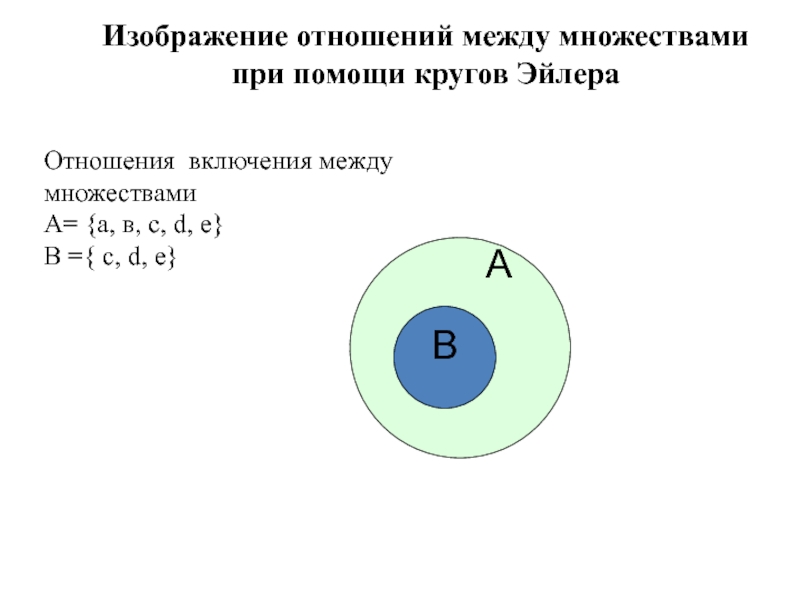
Множество В называется подмножеством множества А, если каждый элемент множества В является также элементом множества А.
В⊂А - «В подмножество А», «В включается в А»
Слайд 29Отношения между множествами
{∅}-?
Приведите пример множества, у которого подмножеством
будет {∅}
{∅} является подмножеством любого заданного множества А
Среди
всех подмножеств заданного множества А должно быть обязательно {∅} и само множество А
Выпишем все подмножества мн-ва А ={2,3,4}
{2} {3} {4}
{2,3} {2,4} {3,4}
{2,3,4}
{∅}
Слайд 30Равные множества А=В
A= {а, в, с, d, е}
В ={а, в,
с, d, е}
Пересекаются
Каждый элемент мн-ва А яв-ся элементом мн-ва В
А В
Каждый элемент мн-ва В яв-ся элементом мн-ва А
В А
Множества А и В называются равными, если А-подмножество В и В-подмножество А. ( А=В)
Слайд 31Задания
№ 3. Дано множество Р={3, 5, 7, 9}.
Образуй все возможные
подмножества множества Р.
{3} {5} {7} {9}
{3,5} {3,7} {3,9} {5,7} {5,9}
{7,9}
{3,5,7} {3,5,9} {5,7,9}
{3,5,7,9}
{∅}
№ 4. Найди и запиши равные множества.
В={123, 213, 312, 132, 321};С={312,321,231,213,123}; Е={132, 321, 123, 213, 312};
В=Е
Слайд 32 А
Изображение отношений между множествами при помощи
кругов Эйлера
В
Отношения включения между множествами
A= {а, в,
с, d, е}
В ={ с, d, е}
Слайд 33 А
Изображение отношений между множествами при помощи
кругов Эйлера
В
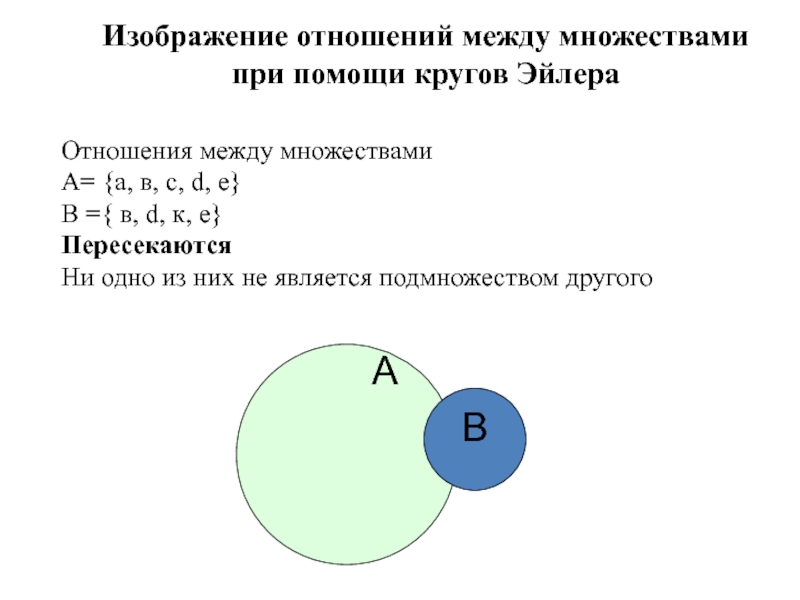
Отношения между множествами
A= {а, в, с,
d, е}
В ={ в, d, к, е}
Пересекаются
Ни одно из них не является подмножеством другого
Слайд 34 А
Изображение отношений между множествами при помощи
кругов Эйлера
В
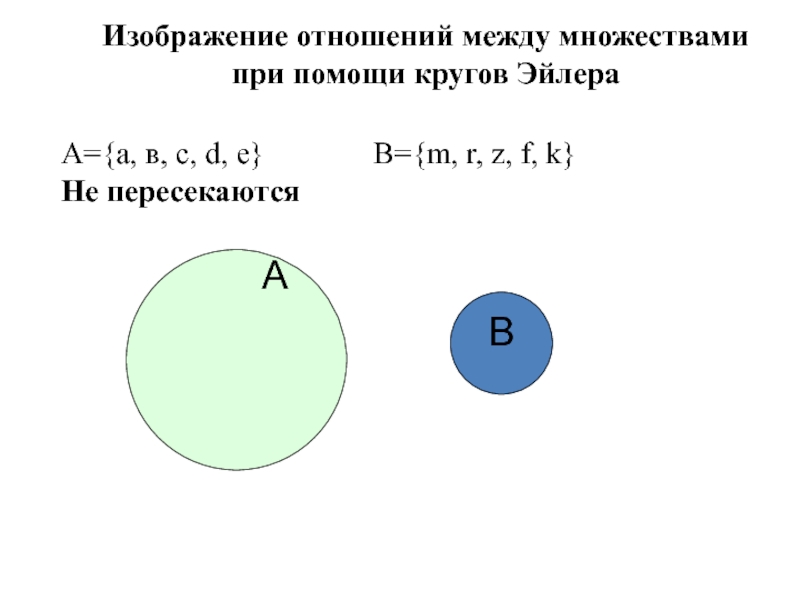
A={а, в, с, d, е}
В={m, r, z, f, k}
Не пересекаются
Слайд 35 А
В
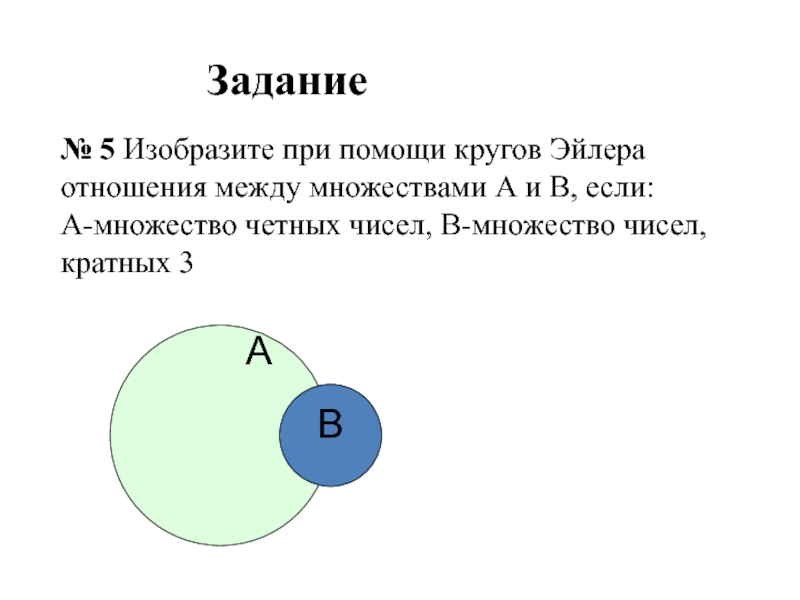
Задание
№ 5 Изобразите при
помощи кругов Эйлера отношения между множествами А и В, если:
А-множество
четных чисел, В-множество чисел, кратных 3
Слайд 36
А=В
Задание
№ 6 Изобразите при помощи кругов
Эйлера отношения между множествами А и В, если:
А-множество квадратов, В-множество
прямоугольников с равными сторонами
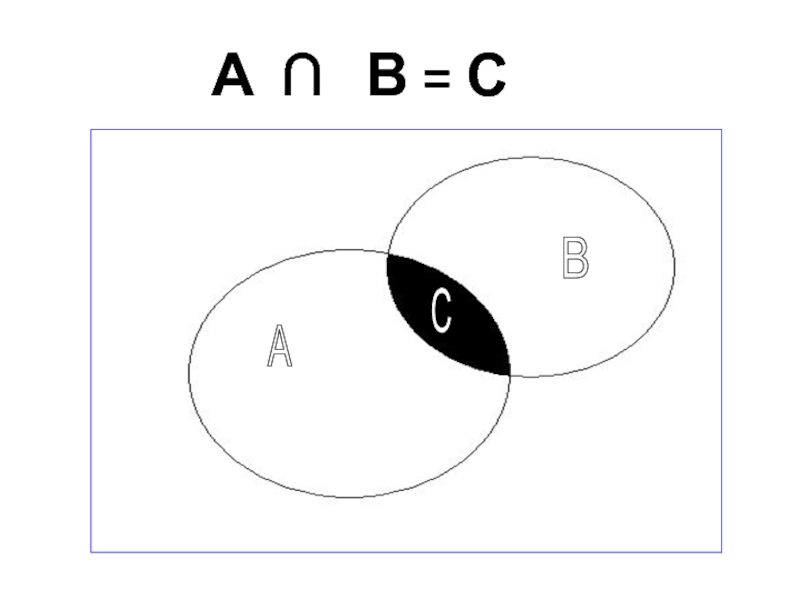
Слайд 38Пересечением множеств А и В называется…
множество, содержащее только такие элементы,
которые принадлежат множеству А и множеству В.
Слайд 39
А ∩ В = ∅
Множества А и В не
имеют общих элементов-пересечение пусто
Чтобы найти А ∩ В достаточно
перечислить элементы, которые принадлежат А и В, т.е их общие элементы
Если множества А и В заданы с помощью характеристических св-в, то характеристическое св-во мн-ва А ∩ В составляется из характеристических св-в пересекаемых мн-в с помощью союза «И»
Слайд 40Мн-во А –четные натуральные числа
Мн-во В –двузначные натуральные числа
Характеристическое св-во
эл-тов мн-ва А
«быть четным натуральным числом»
Характеристическое св-во эл-тов мн-ва В
«быть
двузначным натуральным числом»
Характеристическое св-во элементов
А ∩ В ?
«быть четным и двузначным натуральным числом»
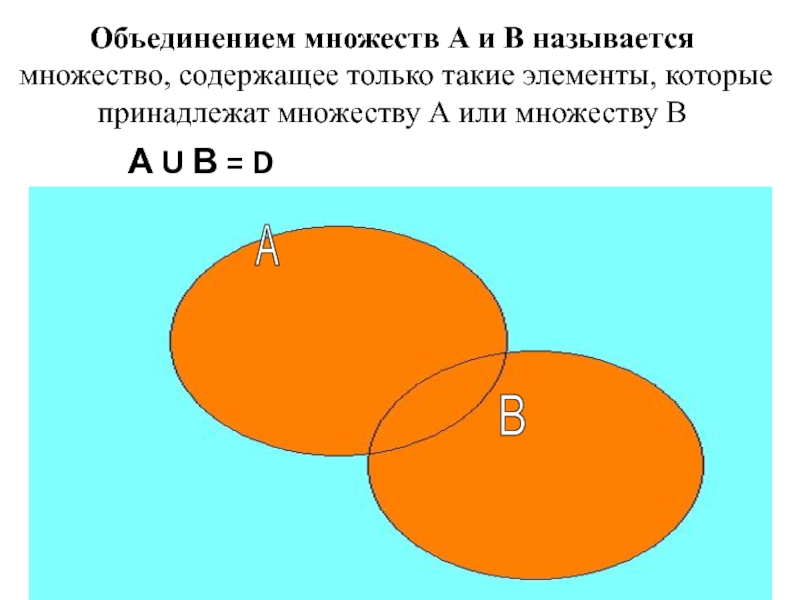
Слайд 41 А U В = D
Объединением множеств А и
В называется
множество, содержащее только такие элементы, которые принадлежат множеству
А или множеству В
А
В
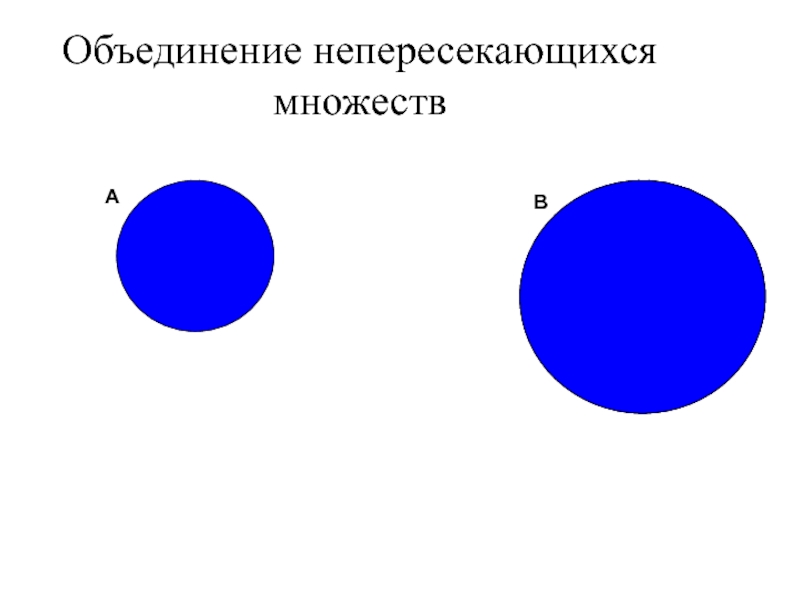
Слайд 42Объединение непересекающихся множеств
В
А
Слайд 43Если эл-ты мн-ва А и В перечислены, то, чтобы найти
объединение мн-в А U В достаточно перечислить элементы, принадлежащие А
или В, т.е хотя бы одному из мн-в
A={2, 4, 6, 8} B={ 5, 6, 7,8,9}
А U В =?
А U В ={ 2,4,5, 6, 7,8,9}
Слайд 44Если множества А и В заданы с помощью характеристических св-в,
то характеристическое св-во мн-ва А U В составляется из характеристических
св-в мн-в с помощью союза «ИЛИ»
Слайд 45Мн-во А –четные числа
Мн-во В –двузначные числа
Характеристическое св-во эл-тов мн-ва
А
«быть четным числом»
Характеристическое св-во эл-тов мн-ва А
«быть двузначным числом»
Характеристическое св-во
элементов
А U В ?
«быть четным или двузначным числом»
Сколько таких чисел?
Таких чисел бесконечное множество. Характеристическое св-во позволяет узнать содержится тот или иной эл-т в А U В или нет
Слайд 46Задание № 7
Мн-во А –четные числа
Мн-во В –двузначные числа
Выпишите числа,
которые принадлежат А U В
8, 13, 1357,36
Слайд 47«ГЕОМЕТРИЯ» «ГЕОГРАФИЯ»
Задание № 8
Даны 2 мн-ва букв, из которых
составлены слова «геометрия» и «география»
Выпишите буквы, которые являются пересечением и
объединением этих 2 мн-в
Слайд 48
«ПЕРЕСЕЧЕНИЕ ЭТИХ МНОЖЕСТВ СОСТОИТ ИХ БУКВ:
Г Е О Р
Ф И Я
ОБЪЕДИНЕНИЕ СОСТОИТ ИЗ БУКВ: Г Е О
М Е Т Р И Я А Ф
«ГЕОМЕТРИЯ»«ГЕОГРАФИЯ» проверьте правильность выполнения задания:
Слайд 49Вместо многоточия поставьте «и» либо «или»:
Элемент х принадлежит объединению множеств
P и Q тогда и только тогда, когда он принадлежит
множеству P…множеству Q
Элемент х не принадлежит объединению множеств P и Q тогда и только тогда, когда он не принадлежит множеству P… не принадлежит множеству Q
Элемент х принадлежит пересечению множеств P и Q тогда и только тогда, когда он принадлежит множеству P…множеству Q
Элемент х не принадлежит пересечению множеств P и Q тогда и только тогда, когда он не принадлежит множеству P… не принадлежит множеству Q
Слайд 50Дополнение
Пусть В-подмножество А, т.е. В⊂А.
Дополнением множества В до множества
А называется множество, содержащее только те элементы множества А, которые
не принадлежат множеству В.
А\В
Операция, при помощи которой находят дополнение подмножества, называется вычитанием
Х А \ В Х А и Х В
В случае, когда В является подмножеством А, т.е. В⊂А, разность А\В называется дополнением множества В до множества А (или относительно множества А).
Слайд 51Дополнение
Если эл-ты мн-ва А и В перечислены, то чтобы найти
А\В, достаточно перечислить эл-ты, принадлежащие А и не принадлежащие В
A=
{1, 2, 3, 5}
В ={ 1, 5}
А\В= ?
А\В={ 2, 3}
Если указаны характеристические св-ва эл-тов мн-в А и В (В⊂А), характеристическое св-во мн-ва А\В имеет вид «Х А и Х В»
Слайд 52Задание
А- множество четных чисел
В-множество чисел, кратных 4
Найдите А\В
Определите содержатся ли
в этом дополнении числа 20 и 26
Все числа, кратные 4-
четные, значит В⊂А
Если из мн-ва А удалить все числа, кратные 4, то в нем останутся четные числа, не кратные 4.
Значит А\В –мн-во четных чисел, не кратных 4. Характеристическое св-во элементов этого мн-ва «быть четным числом и не кратным 4»
20-? 26-?
Слайд 53Задание № 9
1)Найдите А∪В, А∩В, А\В, В\А, если: А={1,2,4,6}
В={6,16,26}
А∪В={1,2,4,6,16,26}
А∩В={6}
А\В={1,2,4}
В\А={16,26}
Слайд 54Классификация-?
Это действие распределения объектов по классам на основании сходств объектов
внутри класса и их отличия от объектов других классов
Цель классификации-
систематизация наших знаний.(биология: виды животных ботаника-классификация растений, математика- углы, натуральные числа)
Слайд 55
Каким условиям должна удовлетворять правильно выполненная классификация?
Считают, что множество Х разбито на классы Х1, Х2,…,Хn,если:
1)
подмножества Х1, Х2,…,Хn попарно не пересекаются
2) объединение подмножеств Х1, Х2, …, Хn совпадает с множеством Х
Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.
Слайд 56Классификация связана с выделением из множества его подмножеств.
Для этого достаточно
указать характеристическое св-во его элементов
Рассмотрим мн-во N (четные,нечетные,кратные 3, 5
и т.д)
Предположим нас интересуют нат.числа, обладающие св-вом «делиться на 3»
Выделяем из N подмножество чисел, кратных 3
Остальные нат.числа не кратны 3. Это еще одно подмножество N
Эти 2 подмножества не пересекаются,а их объединение совпадает с мн-вом N
Задание одного св-ва эл-тов N привело к разбиению этого мн-ва на 2 класса(кратных 3;не кратных 3)
Слайд 57Разбиение мн-ва на классы, если указаны
2св-ва(выделение из мн-ва 2
различных подмн-ва)
Дано N
Выделим 2 св-ва «быть кратным 3»; «быть кратным
5»
Эти св-ва позволяют из N выделить 2 подмножества: А-числа,кратные 3 и В-числа,кратные 5.
1.Эти подмножества пересекаются
2.Ни одно из них не является подмножеством другого
Выделение двух св-в нат.чисел привело к разбиению мн-ва N на 4 класса:
1) кратных 3 и 5; 2) кратных 3, но не кратных 5; 3) кратных 5, но не кратных 3 4) не кратных 5 и не кратных 3
Слайд 58Задания
Разбейте множество целых чисел на классы с помощью одного свойства.
Установите
правильны ли следующие классификации:
а) множество натуральных чисел делится на однозначные,
двузначные и трехзначные числа
б) параллелограммы могут быть прямоугольниками, квадратами и ромбами
в) треугольники бывают равносторонними и неравносторонними
г) четырехугольники делятся на параллелограммы и трапеции
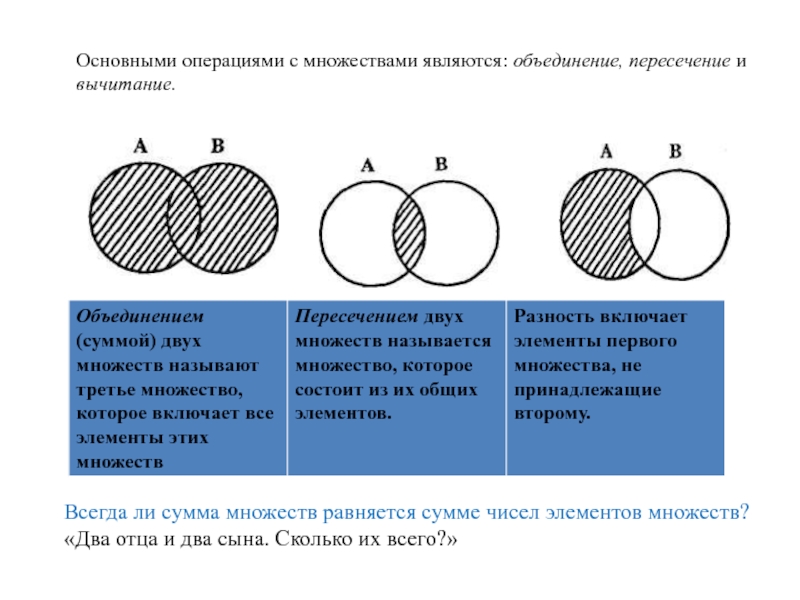
Слайд 59Основными операциями с множествами являются: объединение, пересечение и вычитание.
Всегда ли
сумма множеств равняется сумме чисел элементов множеств?
«Два отца и два
сына. Сколько их всего?»
Слайд 61Счет объектов
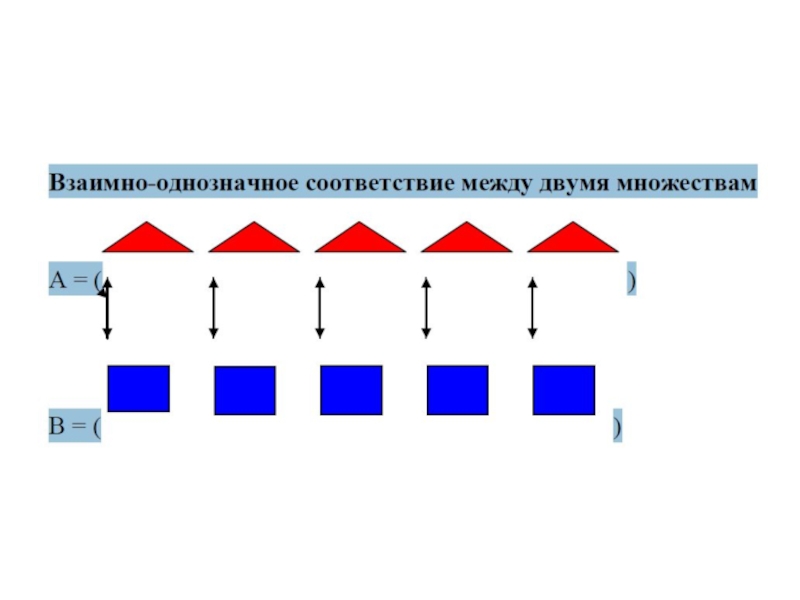
Счет – это процесс установления взаимно-однозначного соответствия между
элементами заданного конечного множества и числами –элементами начального отрезка натурального
ряда , при котором каждое названное число характеризует рассмотренное подмножество элементов заданного множества, а последнее названное число характеризует все заданное множество .
В истории развития человечества долгое время использовался дочисловой счет. Человек сравнивал множества, констатировал их равночисленность (равенство) или не равночисленность (столько же, меньше, больше...).
С появлением натуральных чисел человек в качестве одного из множеств стал использовать числовой ряд
Слайд 62Число — показатель мощности прерывной (множества) или непрерывной величины.
Число
всегда есть отношение этой величины к избранной мере, поэтому число
не является постоянной характеристикой, оно относительно к той единице, которая принимается за меру (считать можно парами, десятками;
измерять можно разными мерами — результат будет разный).
Число и цифра
Число – показатель мощности множества, т.е. того, сколько элементов содержит множество
Цифра- символ, знак числа.
Слайд 63Понятие «величина» в математике рассматривается как основное.
Величина — это
и протяженность, и объем, и скорость, и масса, и число,
и т.д.
Величина является свойством предмета, воспринимаемым различными анализаторами: зрительным, тактильным и двигательным.
Величина предмета, т.е. размер предмета, определяется только на основе сравнения.
Восприятие величины зависит от расстояния, с которого предмет воспринимается, а также от величины предмета, с которым он сравнивается.
Характеристика величины предмета зависит также от расположения его в пространстве.
Величина конкретного предмета характеризуется такими особенностями: сравнимость, изменчивость и относительность.
Слайд 64Величина предмета определяется человеком только в сравнении с другой величиной
— мерой.
Мера является эталоном величины. В качестве эталонов величины
выступают наши представления об отношениях между предметами и обозначаются словами, указывающими на место предмета среди других (большой, маленький, высокий, длинный, короткий, толстый, тонкий и т.д.).
Слайд 65Начальному выделению величины, возникновению элементарных представлений о ней способствуют предметные
действия, включающие различные виды непосредственного сопоставления объектов между собой по
их величине (накладывание, прикладывание, приставление), а также опосредованное сравнение с помощью измерения.
Измерение — один из видов математической деятельности. С помощью измерения определяется непрерывная величина: масса, объем, протяженность.
Основной момент в обучении измерению — ознакомление детей с мерой.
Введение измерения в программу воспитания в детском саду решает две цели:
- познакомить детей с мерой и научить измерять, сравнивать предметы по величине,
- показать детям зависимость между мерой, ее величиной и результатом — количеством измерений.
Слайд 66Классическая дидактика выделила величину и форму как самостоятельные категории действительности.
Уровень познания формы весьма существен, так как на него опираются
при формировании представлений о величине, пространстве и др.
Исходным содержанием понятия о форме служат реальные предметы окружающей действительности.
Первые представления о форме конкретных предметов дает ребенку взрослый, воспитатель. Однако на определенном этапе развития у ребенка возникает потребность как-то разобраться в разнообразии форм. Этот процесс осуществляется первоначально в результате уподобления одного предмета по форме другому. Например, дети, рассматривая какой-то предмет, говорят: похожий на огурчик, на морковку. Постепенно возникает необходимость построить некоторые доступные детям обобщения, являющиеся не чем иным, как усвоением определенной классификации геометрических фигур.
Слайд 67Образцами — эталонами формы выступают геометрические фигуры. Они являются абстрагированием
от формы реальных предметов.
С помощью геометрических фигур проводится анализ
окружающей действительности по форме.
Восприятие ребенком окружающих предметов на первых порах еще не означает выделение им формы. Для ребенка сначала выступает сам предмет, а не особенности его формы. Ознакомление детей с системой геометрических фигур создает у них обобщенные представления о форме.
Слайд 68Основные понятия геометрии
Краткая характеристика основных понятий планиметрии
Плоские фигуры
Краткая
характеристика основных понятий стереометрии
Объемные фигуры (тела)
Слайд 71Основные понятия геометрии
Точка — неопределяемое понятие геометрии, элемент пространства. Считается,
что точка не имеет ни длины, ни ширины, ни площади.
Прямая
– основное неопределяемое понятие, подмножество пространства.
Плоскость – основное неопределяемое понятие, специальное подмножество пространства.
Геометрическая фигура – множество точек.
Свойства и взаимосвязи основных понятий описываются с помощью определенной группы аксиом.
Через основные понятия вводятся определения всех других геометрических понятий.
На основании аксиом и определений доказывают теоремы.
Слайд 72Некоторые характеристические
свойства плоскости
Плоскость — поверхность,
содержащая полностью каждую
прямую, соединяющую
любые её точки;
Две
плоскости являются либо параллельными, либо пересекаются по прямой.
Прямая либо
параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.
Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.
Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.
Слайд 73Краткая характеристика
основных понятий планиметрии
Планиметрия – раздел геометрии, изучающий свойства
фигур, лежащих в одной плоскости.
Если все точки фигуры принадлежат одной
плоскости, то фигура называется плоской.
Линия — неопределяемое понятие геометрии.
Прямую линию удобно моделировать, сгибая любой лист бумаги.
Основное свойство прямой линии: прямая линия бесконечна.
Кривую линию удобно моделировать из шнура. Кривая линия также бесконечна (если она не замкнутая).
Линии могут быть замкнутыми и незамкнутыми.
Линии могут быть расположены на плоскости и в пространстве.
Основные взаимоотношения точки и линии:
1. Через одну точку можно провести множество прямых.
2. Через одну точку можно провести множество кривых.
3. Через две точки можно провести только одну прямую.
4. Через две точки можно провести множество кривых.
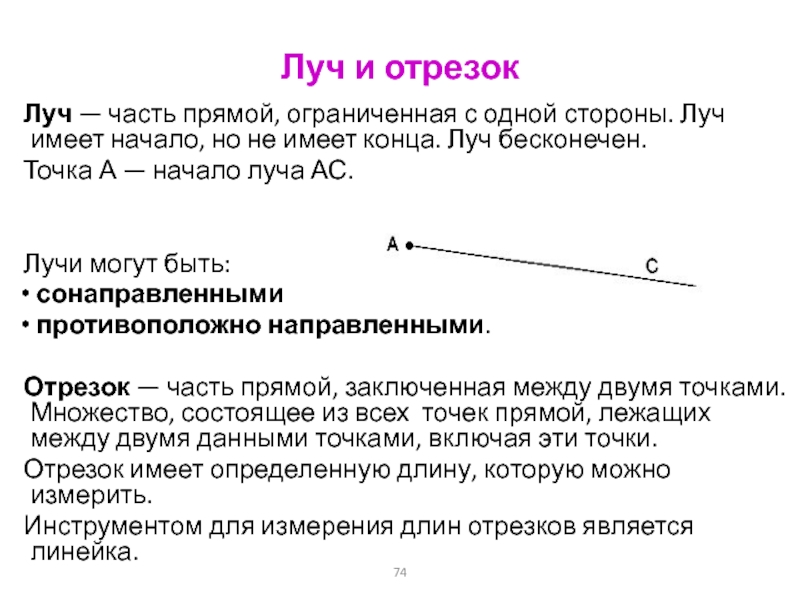
Слайд 74Луч и отрезок
Луч — часть прямой, ограниченная с одной стороны.
Луч имеет начало, но не имеет конца. Луч бесконечен.
Точка А
— начало луча АС.
Лучи могут быть:
сонаправленными
противоположно направленными.
Отрезок — часть прямой, заключенная между двумя точками. Множество, состоящее из всех точек прямой, лежащих между двумя данными точками, включая эти точки.
Отрезок имеет определенную длину, которую можно измерить.
Инструментом для измерения длин отрезков является линейка.
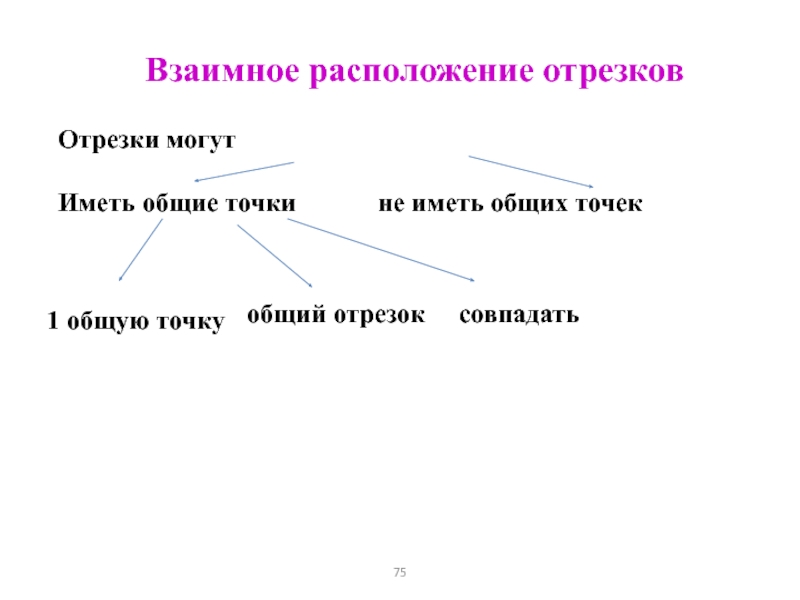
Слайд 75Взаимное расположение отрезков
Отрезки могут
Иметь общие точки не иметь общих точек
1 общую
точку
общий отрезок
совпадать
Слайд 76Углы
Угол — это часть плоскости, ограниченная двумя лучами, имеющими
общее начало.
Лучи, образующие угол, называются сторонами угла, а их общее
начало — вершиной угла.
Множество всех точек плоскости между сторонами угла – внутренняя плоскость угла.
Углы равны, если при наложении их стороны совпадают.
Виды углов
По расположению
Два угла, имеющих общую сторону и вершину, являются смежными, если две другие их стороны лежат на одной прямой.
Два угла называются вертикальными, если стороны одного являются дополнительными полупрямыми сторон другого.
По величине (градусной мере)
Угол развернутый – если лучи, выходящие из одной точки, лежат на одной прямой.
Прямой угол - 90°
Тупой угол – больше прямого
Острый угол – меньше прямого
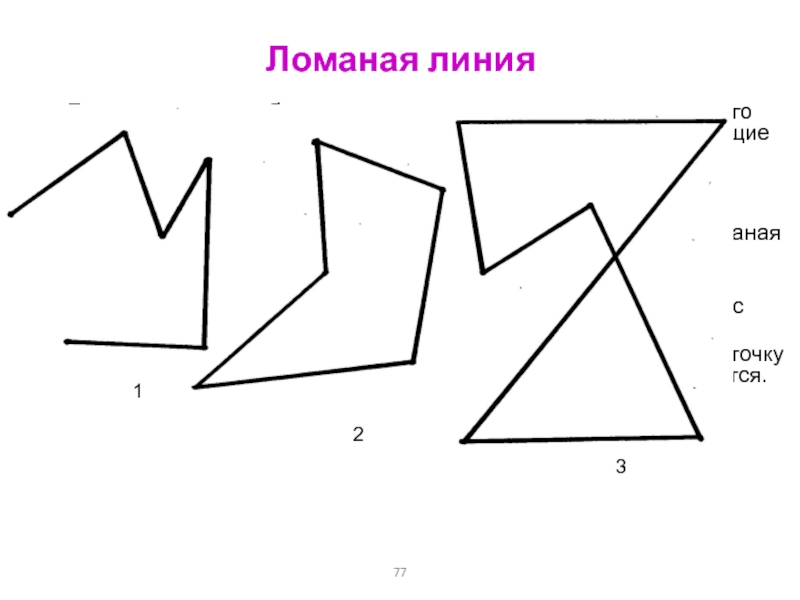
Слайд 77Ломаная линия
Ломаная линия – объединение отрезков, в котором конец каждого
отрезка является началом следующего отрезка, и отрезки, имеющие общий конец,
не лежат на одной прямой.
Отрезки, составляющие ломаную – звенья ломаной.
Точки соединения концов звеньев - вершины ломаной.
Звенья ломаной должны быть соединены последовательно. Ломаная линия содержит конечное число звеньев.
Длина ломаной — сумма длин звеньев ломаной.
Ломаная замкнутая, если конец ее последнего звена совпадает с началом первого звена.
Ломаная простая, если каждое звено имеет только одну общую точку с другим звеном (конец звена). Несмежные звенья не пересекаются.
1
2
3
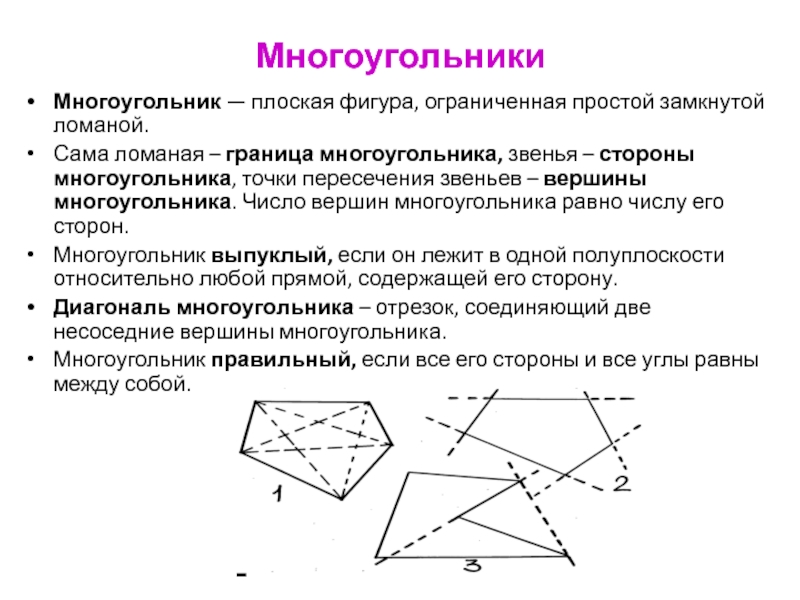
Слайд 78Многоугольники
Многоугольник — плоская фигура, ограниченная простой замкнутой ломаной.
Сама
ломаная – граница многоугольника, звенья – стороны многоугольника, точки пересечения
звеньев – вершины многоугольника. Число вершин многоугольника равно числу его сторон.
Многоугольник выпуклый, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Диагональ многоугольника – отрезок, соединяющий две несоседние вершины многоугольника.
Многоугольник правильный, если все его стороны и все углы равны между собой.
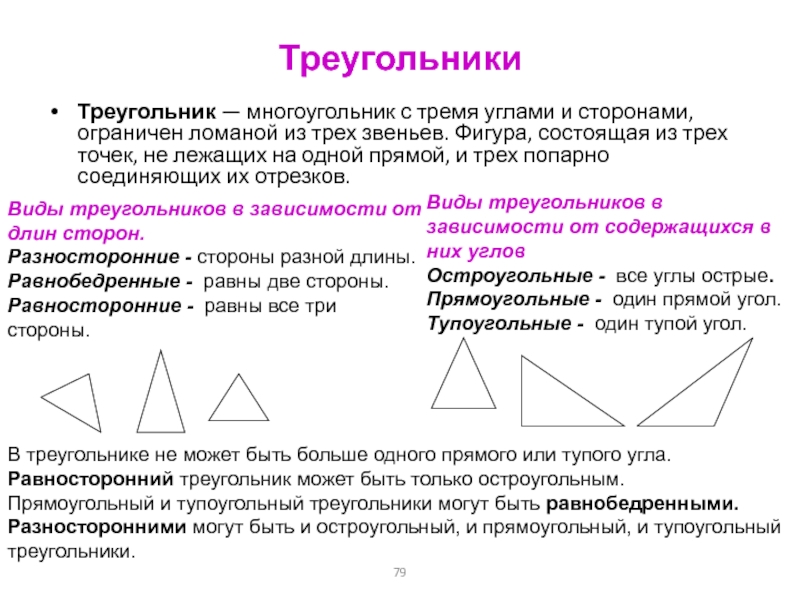
Слайд 79Треугольники
Треугольник — многоугольник с тремя углами и сторонами, ограничен
ломаной из трех звеньев. Фигура, состоящая из трех точек, не
лежащих на одной прямой, и трех попарно соединяющих их отрезков.
Виды треугольников в зависимости от длин сторон.
Разносторонние - стороны разной длины.
Равнобедренные - равны две стороны.
Равносторонние - равны все три стороны.
Виды треугольников в зависимости от содержащихся в них углов
Остроугольные - все углы острые.
Прямоугольные - один прямой угол.
Тупоугольные - один тупой угол.
В треугольнике не может быть больше одного прямого или тупого угла.
Равносторонний треугольник может быть только остроугольным.
Прямоугольный и тупоугольный треугольники могут быть равнобедренными.
Разносторонними могут быть и остроугольный, и прямоугольный, и тупоугольный треугольники.
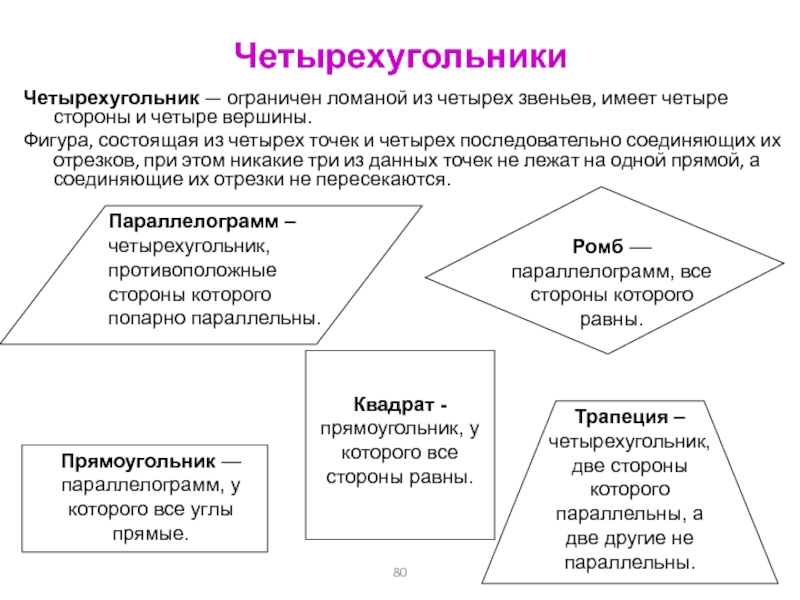
Слайд 80Четырехугольники
Четырехугольник — ограничен ломаной из четырех звеньев, имеет четыре
стороны и четыре вершины.
Фигура, состоящая из четырех точек и
четырех последовательно соединяющих их отрезков, при этом никакие три из данных точек не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
Параллелограмм – четырехугольник, противоположные стороны которого попарно параллельны.
Трапеция –четырехугольник, две стороны которого параллельны, а две другие не параллельны.
Ромб –– параллелограмм, все стороны которого равны.
Прямоугольник — параллелограмм, у которого все углы прямые.
Квадрат - прямоугольник, у которого все стороны равны.
Слайд 81Среди следующих предложений укажите истинные, ответы
обоснуйте:
Если в четырехугольнике
все углы прямые, то этот четырехугольник – прямоугольник;
Если в
четырехугольнике диагонали равны, то этот четырехугольник – прямоугольник;
Если треугольник АВС – равносторонний, то он – равнобедренный;
Если четырехугольник АВСD – квадрат, то он – ромб;
Если трапеция – четырехугольник, то это – параллелограмм.
Слайд 82Окружность и круг
Окружность — это замкнутая кривая линия, состоящая из
точек, находящихся на одинаковом расстоянии от заданной точки О. Множество
всех точек плоскости, находящихся на одном и том же расстоянии от данной точки плоскости.
Точка О называется центром окружности (от лат. «острый конец палочки»).
Радиус — (от лат. «спица колеса») отрезок, соединяющий центр окружности с какой-нибудь ее точкой.
Хорда окружности – отрезок, концы которого принадлежат окружности.
Диаметр окружности — (от гр. «поперечник»)
отрезок (хорда), проходящий через центр окружности
(круга) и соединяющий две любые ее точки.
Диаметр равен двум радиусам.
Круг — часть плоскости, ограниченная окружностью. Множество всех точек плоскости, расстояние которых от некоторой данной точки плоскости (центра) не больше данного.
Граница круга — окружность.
Сектор – часть круга между двумя его радиусами.
Сегмент – часть круга, ограниченная хордой и стягиваемой ею дугой.
Слайд 83Краткая характеристика основных понятий стереометрии
Стереометрия – раздел геометрии, который изучает
свойства всех фигур пространства.
Объемные фигуры в геометрии чаще называют телами.
Геометрическое
тело – ограниченная связная фигура в пространстве, которая содержит все свои граничные точки.
Фигура ограниченная, если ее можно заключить в какую-либо сферу.
Фигура связная, если любые две ее точки можно соединить непрерывной линией, целиком принадлежащей фигуре.
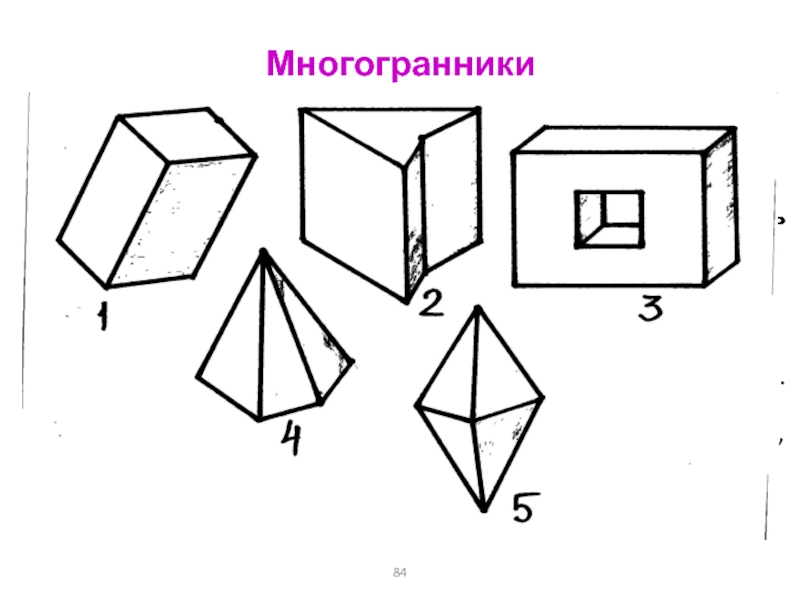
Слайд 84Многогранники
Многогранник – тело, поверхность которого состоит из конечного числа
плоских многоугольников.
Грани многогранника – плоские многоугольники, образующие его поверхность. Ребра
– стороны граней. Вершины многогранников – вершины граней. Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Многогранник выпуклый, если он лежит целиком по одну сторону от плоскости любой его грани. Вместе с двумя любыми точками содержит целиком весь отрезок, соединяющий эти точки. Грани – выпуклые многоугольники.
В любом выпуклом многограннике выполняется условие: b – p + r = 2, где b – число вершин, p – число ребер, r – число граней (теорема Эйлера).
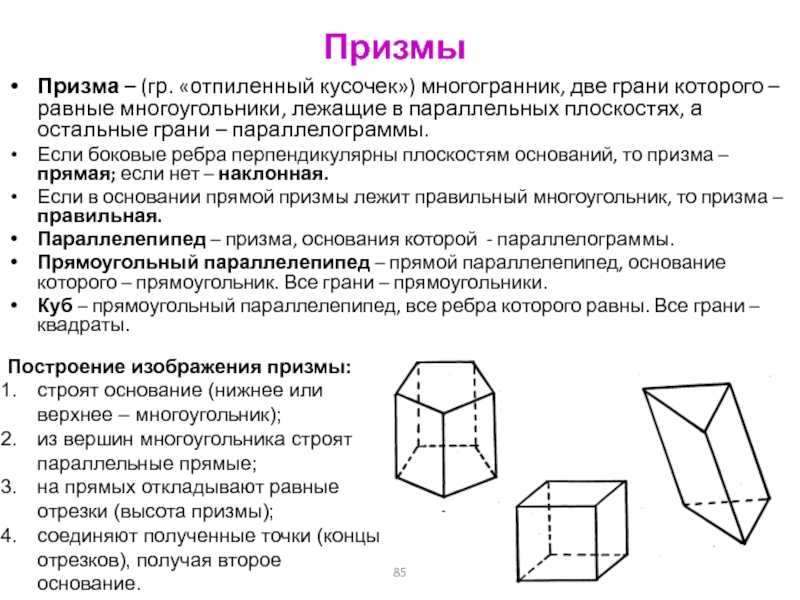
Слайд 85Призмы
Призма – (гр. «отпиленный кусочек») многогранник, две грани которого
– равные многоугольники, лежащие в параллельных плоскостях, а остальные грани
– параллелограммы.
Если боковые ребра перпендикулярны плоскостям оснований, то призма – прямая; если нет – наклонная.
Если в основании прямой призмы лежит правильный многоугольник, то призма – правильная.
Параллелепипед – призма, основания которой - параллелограммы.
Прямоугольный параллелепипед – прямой параллелепипед, основание которого – прямоугольник. Все грани – прямоугольники.
Куб – прямоугольный параллелепипед, все ребра которого равны. Все грани – квадраты.
Построение изображения призмы:
строят основание (нижнее или верхнее – многоугольник);
из вершин многоугольника строят параллельные прямые;
на прямых откладывают равные отрезки (высота призмы);
соединяют полученные точки (концы отрезков), получая второе основание.
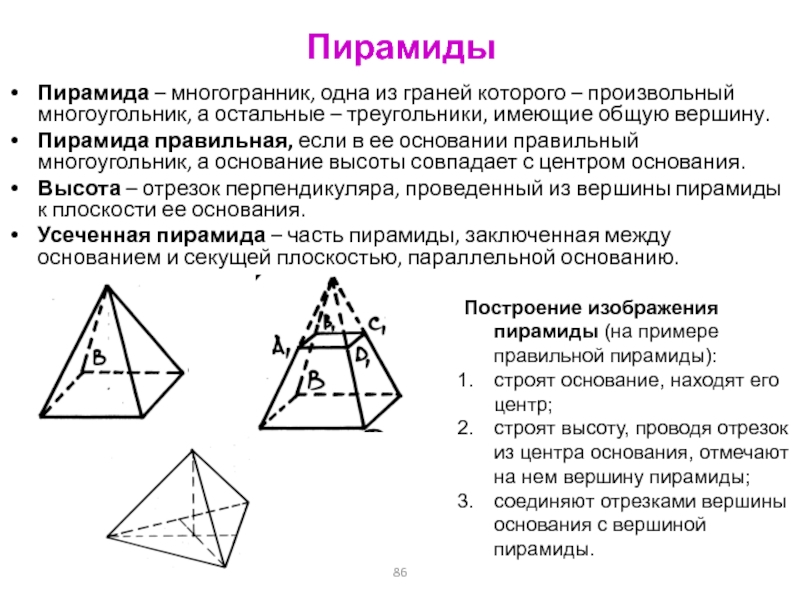
Слайд 86Пирамиды
Пирамида – многогранник, одна из граней которого – произвольный многоугольник,
а остальные – треугольники, имеющие общую вершину.
Пирамида правильная, если в
ее основании правильный многоугольник, а основание высоты совпадает с центром основания.
Высота – отрезок перпендикуляра, проведенный из вершины пирамиды к плоскости ее основания.
Усеченная пирамида – часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию.
Построение изображения пирамиды (на примере правильной пирамиды):
строят основание, находят его центр;
строят высоту, проводя отрезок из центра основания, отмечают на нем вершину пирамиды;
соединяют отрезками вершины основания с вершиной пирамиды.
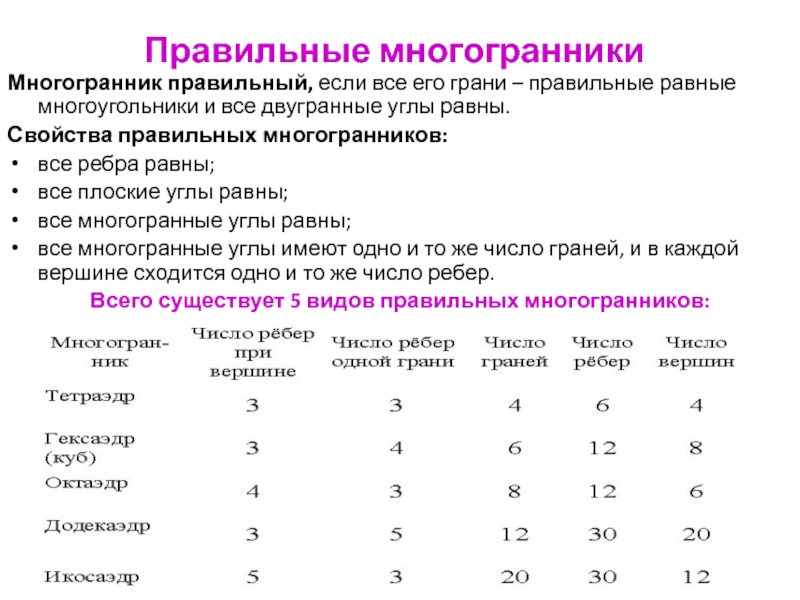
Слайд 87Правильные многогранники
Многогранник правильный, если все его грани – правильные равные
многоугольники и все двугранные углы равны.
Свойства правильных многогранников:
все ребра равны;
все
плоские углы равны;
все многогранные углы равны;
все многогранные углы имеют одно и то же число граней, и в каждой вершине сходится одно и то же число ребер.
Всего существует 5 видов правильных многогранников:
Слайд 88Тетраэдр
Правильная треугольная пирамида
Слайд 89Гексаэдр
Правильный шестигранник,
правильная четырехугольная призма, прямоугольный параллелепипед с равными
ребрами, куб.
Слайд 90Октаэдр
Правильный восьмигранник,
бипирамида четырехугольная
Слайд 91Додекаэдр
Правильный двенадцатигранник
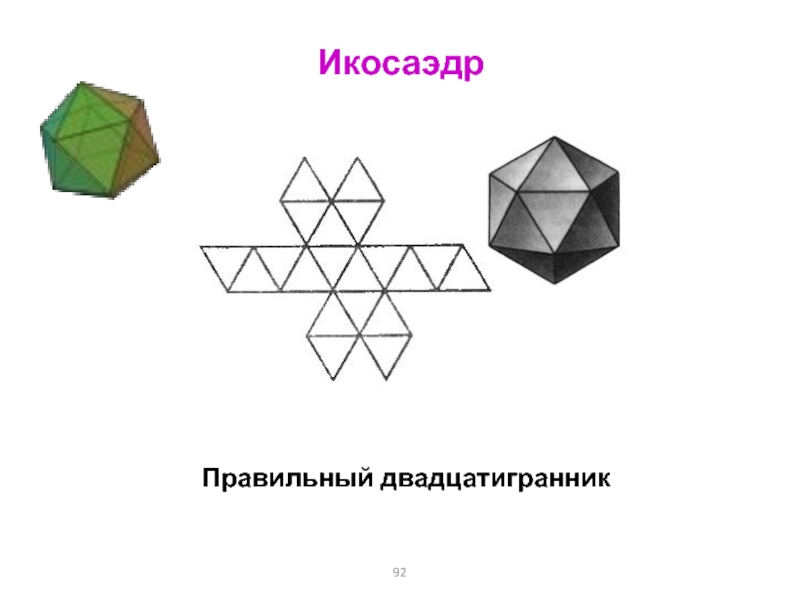
Слайд 92Икосаэдр
Правильный двадцатигранник
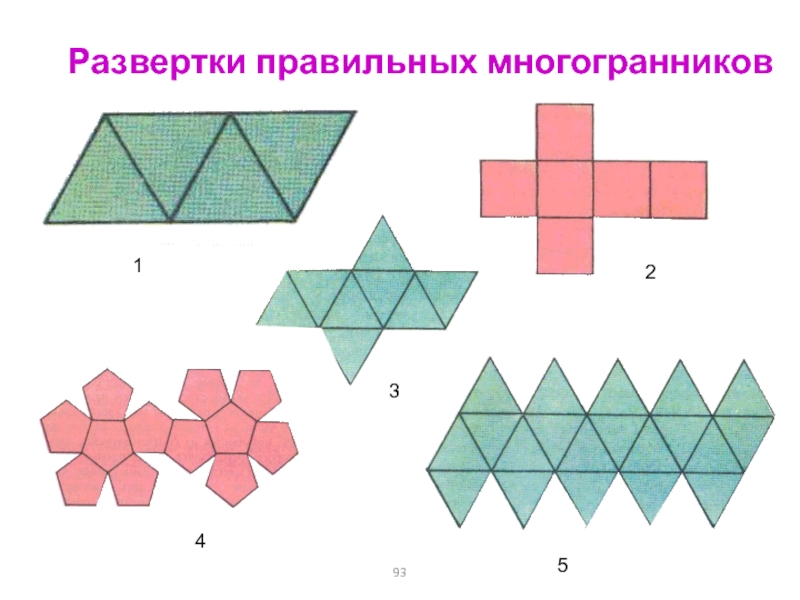
Слайд 93Развертки правильных многогранников
1
2
3
4
5
Слайд 94Тела вращения
Тела вращения образуются при вращении плоской фигуры
вокруг
не пересекающей ее оси, имеют гладкие криволинейные
поверхности.
Прямой круговой цилиндр
(гр. «валик, каток») получается
вращением прямоугольника вокруг одной из сторон.
Прямая, содержащая неподвижную сторону, вокруг которой вращается прямоугольник,
называется осью цилиндра.
Круги, описываемые двумя противоположными вращающимися сторонами,
называются основаниями цилиндра.
Прямой круговой конус (лат. «шишка») –
вращением прямоугольного треугольника вокруг катета.
Прямая, содержащая неподвижный катет, вокруг которого поворачивается треугольник,
называется осью конуса.
Круг, описываемый вращающимся катетом, называется основанием конуса.
Вершина треугольника, не лежащая в плоскости основания, называется вершиной конуса.
Отрезок, соединяющий вершину конуса и точку на окружности основания, называется
образующей конуса. Все образующие конуса равны.
Шар – вращением полукруга вокруг диаметра.
Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара.
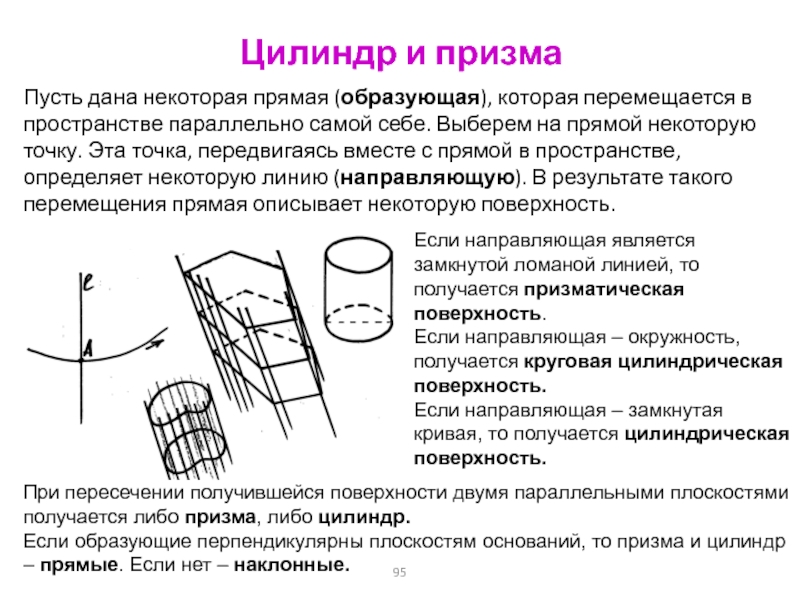
Слайд 95Цилиндр и призма
Пусть дана некоторая прямая (образующая), которая перемещается в
пространстве параллельно самой себе. Выберем на прямой некоторую точку. Эта
точка, передвигаясь вместе с прямой в пространстве, определяет некоторую линию (направляющую). В результате такого перемещения прямая описывает некоторую поверхность.
Если направляющая является замкнутой ломаной линией, то получается призматическая поверхность.
Если направляющая – окружность, получается круговая цилиндрическая поверхность.
Если направляющая – замкнутая кривая, то получается цилиндрическая поверхность.
При пересечении получившейся поверхности двумя параллельными плоскостями получается либо призма, либо цилиндр.
Если образующие перпендикулярны плоскостям оснований, то призма и цилиндр – прямые. Если нет – наклонные.
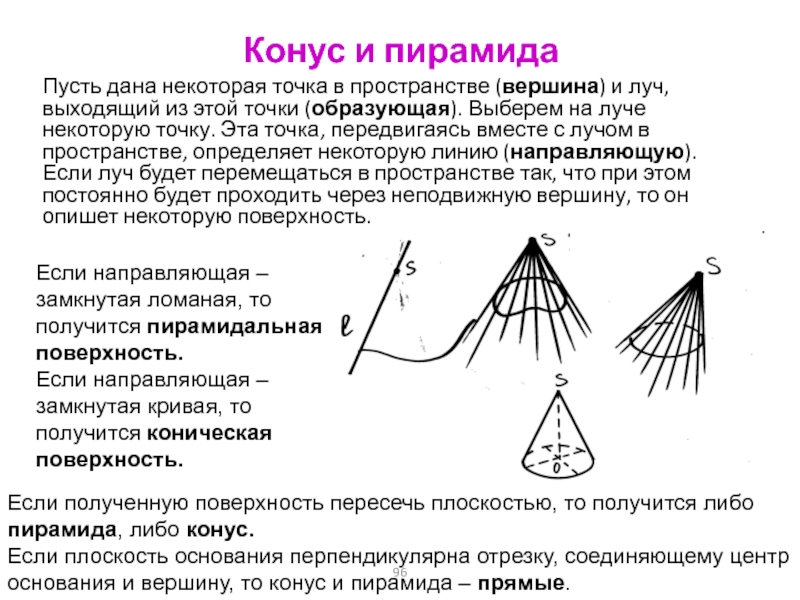
Слайд 96Конус и пирамида
Пусть дана некоторая точка в пространстве (вершина) и
луч, выходящий из этой точки (образующая). Выберем на луче некоторую
точку. Эта точка, передвигаясь вместе с лучом в пространстве, определяет некоторую линию (направляющую). Если луч будет перемещаться в пространстве так, что при этом постоянно будет проходить через неподвижную вершину, то он опишет некоторую поверхность.
Если направляющая – замкнутая ломаная, то получится пирамидальная поверхность.
Если направляющая – замкнутая кривая, то получится коническая поверхность.
Если полученную поверхность пересечь плоскостью, то получится либо пирамида, либо конус.
Если плоскость основания перпендикулярна отрезку, соединяющему центр основания и вершину, то конус и пирамида – прямые.
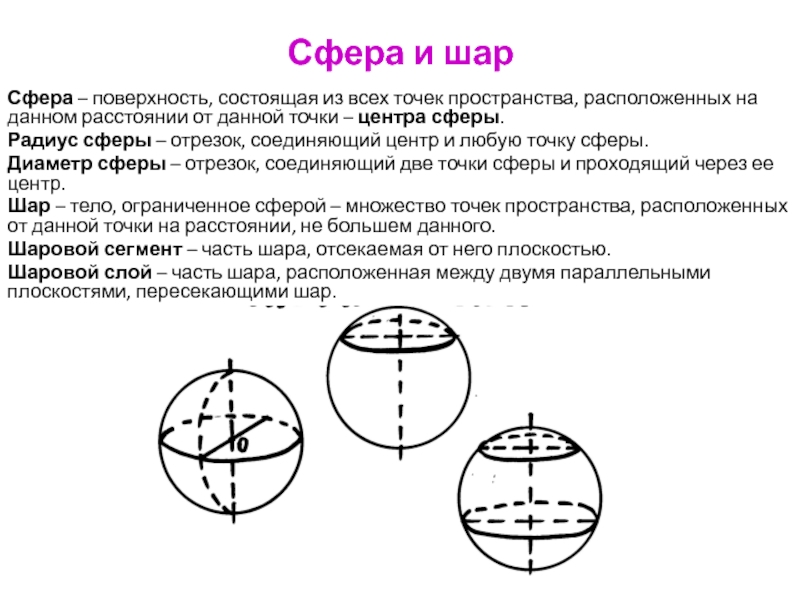
Слайд 97Сфера и шар
Сфера – поверхность, состоящая из всех точек
пространства, расположенных на данном расстоянии от данной точки – центра
сферы.
Радиус сферы – отрезок, соединяющий центр и любую точку сферы.
Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через ее центр.
Шар – тело, ограниченное сферой – множество точек пространства, расположенных от данной точки на расстоянии, не большем данного.
Шаровой сегмент – часть шара, отсекаемая от него плоскостью.
Шаровой слой – часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.
Слайд 98Выбери правильный ответ
1. Конус и цилиндр – это 2. Конус
получается вращением
а) плоские фигуры а) любого треугольника
б) многогранники
б) прямоугольного треугольника
в) тела вращения в) многоугольника
3. Цилиндр получается вращением 4. Шар получается вращением
а) прямоугольника а) сегмента
б) многоугольника б) полукруга
в) треугольника в) окружности
Слайд 99
Понятие симметрии
«Симметрия» в переводе с греческого означает «соразмерность» (повторяемость).
Симметричным наз.
объект,
который можно как-то
изменять, получая в
результате то же,
с чего начали. Герман Вейль
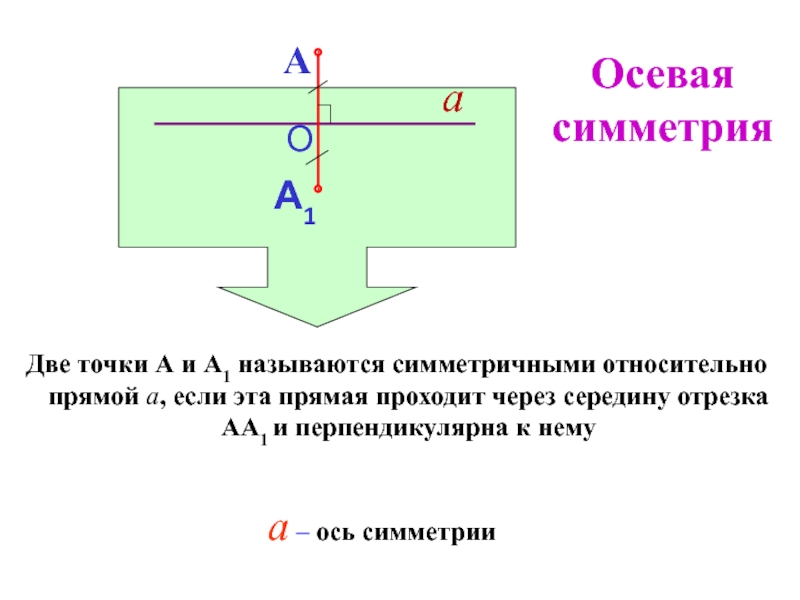
Слайд 100Две точки А и А1 называются симметричными относительно прямой а,
если эта прямая проходит через середину отрезка АА1 и перпендикулярна
к нему
А
А1
а
О
а – ось симметрии
Осевая симметрия
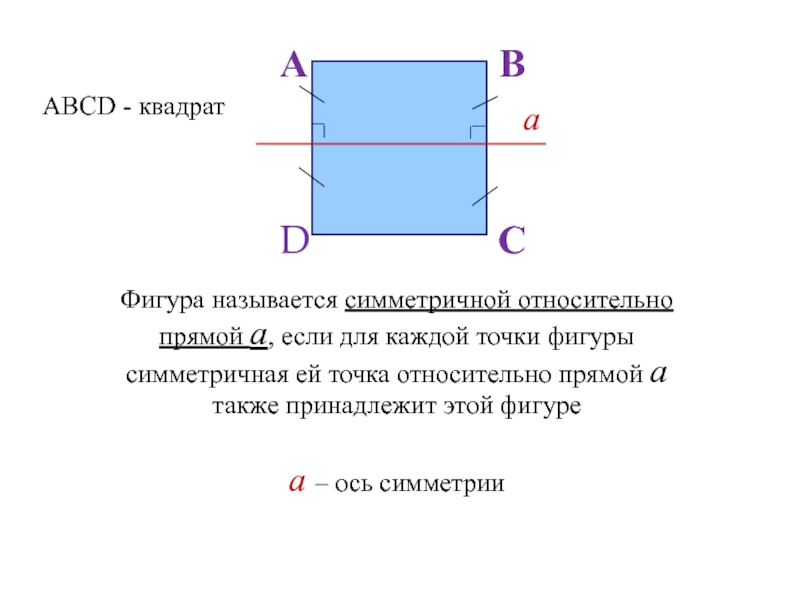
Слайд 101Фигура называется симметричной относительно прямой а, если для каждой точки
фигуры симметричная ей точка относительно прямой а также принадлежит этой
фигуре
а – ось симметрии
А
В
С
D
а
АВСD - квадрат
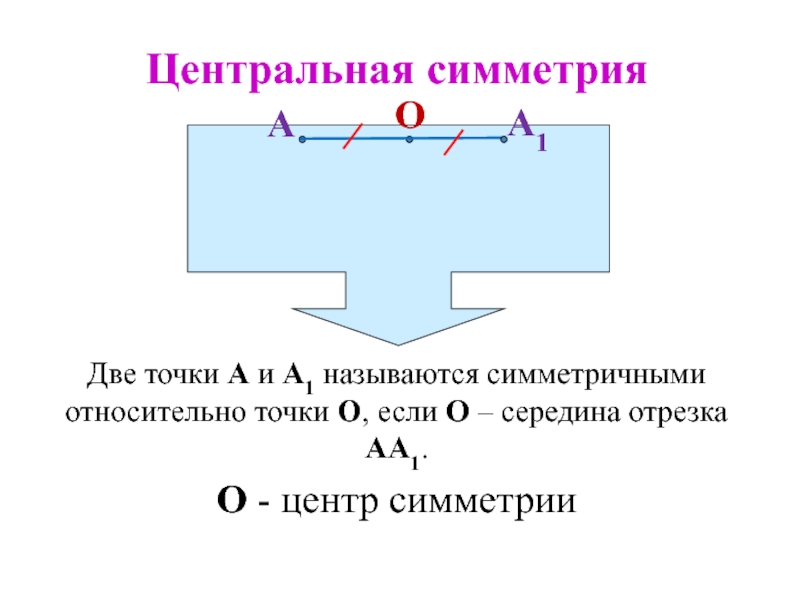
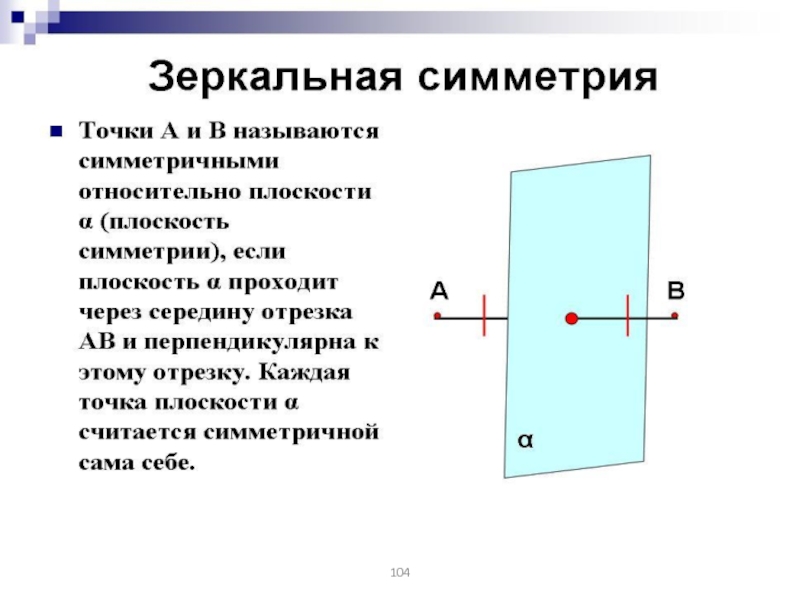
Слайд 102Две точки А и А1 называются симметричными относительно точки О,
если О – середина отрезка АА1.
О - центр симметрии
А
О
А1
Центральная симметрия
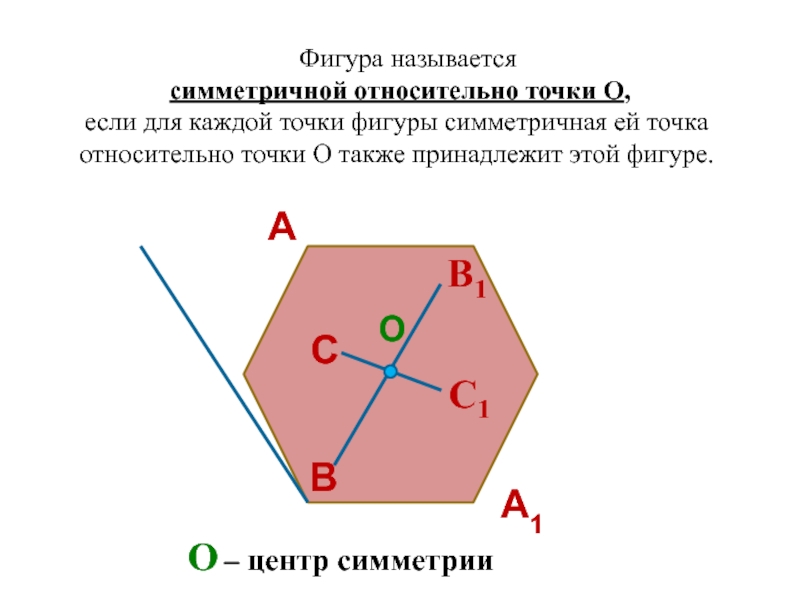
Слайд 103 Фигура называется
симметричной относительно точки О,
если для
каждой точки фигуры симметричная ей точка относительно точки О также
принадлежит этой фигуре.
О
В
А
С
А1
В
1
С
1
О – центр симметрии
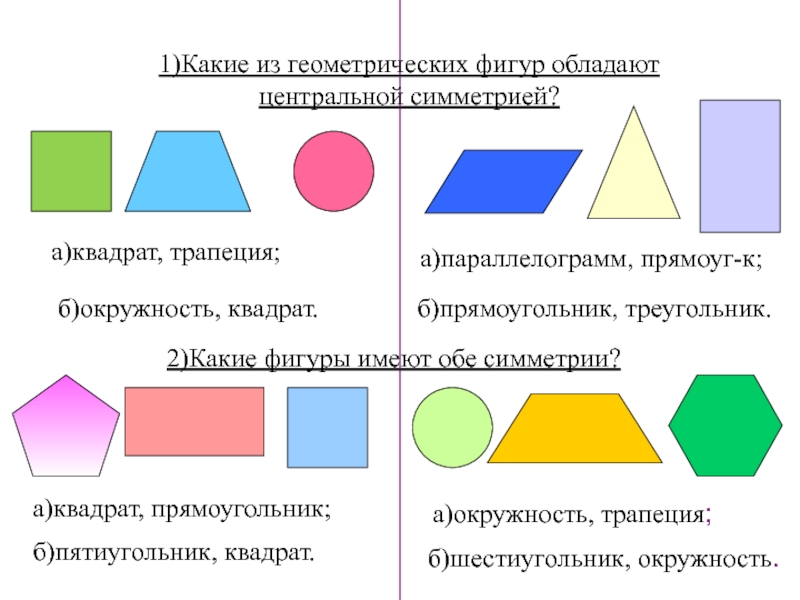
Слайд 1061)Какие из геометрических фигур обладают центральной симметрией?
2)Какие фигуры имеют обе
симметрии?
а)квадрат, трапеция;
б)окружность, квадрат.
а)параллелограмм, прямоуг-к;
б)прямоугольник, треугольник.
а)квадрат, прямоугольник;
а)окружность, трапеция;
б)пятиугольник, квадрат.
б)шестиугольник, окружность.
Слайд 107
В презентации использованы материалы
Габовой Марины Анатольевны
канд. пед. наук, доцент кафедры
ПМДО КГПИ
Слайд 108Технология математического образования -последовательную систему действий педагога по планированию, применению
и оцениванию всего процесса взаимодействия с ребенком посредством специально отобранной
совокупности содержания, методов, средств, форм обучения математике, видов деятельности, соответствующих возрастным особенностям познания математической действительности детьми дошкольного возраста.
В технологии эта последовательность действий педагога обеспечивает гарантированное достижение поставленных целей, комфортные условия педагогу и ребенку.
Слайд 109Содержание математического развития дошкольников
Под содержанием обучения понимается объем и
характер знаний, умений и навыков, которыми должны овладеть дети в
процессе организации разных видов деятельности.
В программах представлены три направления:
-представления и понятия;
-зависимости и отношения;
-математические действия.
Слайд 110Основные представления и понятия:
«количество», «число», «множество», «подмножество», «величина», «мера»,
«форма предмета». «геометрические фигуры»; представления о пространстве и времени.
Каждое
математическое понятие формируется поэтапно, по линейно-концентрическому принципу. Разные математические понятия тесно связаны между собой. В дошкольном возрасте основные математические понятия вводятся описательно, без всяких определений и даже описания этих понятий.
Каждое понятие вводится наглядно, путем созерцания конкретных предметов или практического оперирования ими.
Слайд 111Математические зависимости и отношения:
отношения между предметными множествами (равночисленность – неравночисленность),
отношение порядка в натуральном ряду, временные отношения; зависимости между свойствами
геометрических фигур, между величиной, мерой и результатом измерения и др.
Слайд 112В методике выделяются две группы математических действий:
-основные ( счет,
измерение, вычисления);
-дополнительные, пропедевтические, сконструированные в дидактических целях (практическое сравнение,
наложение, приложение; уравнивание и комплектование; сопоставление )
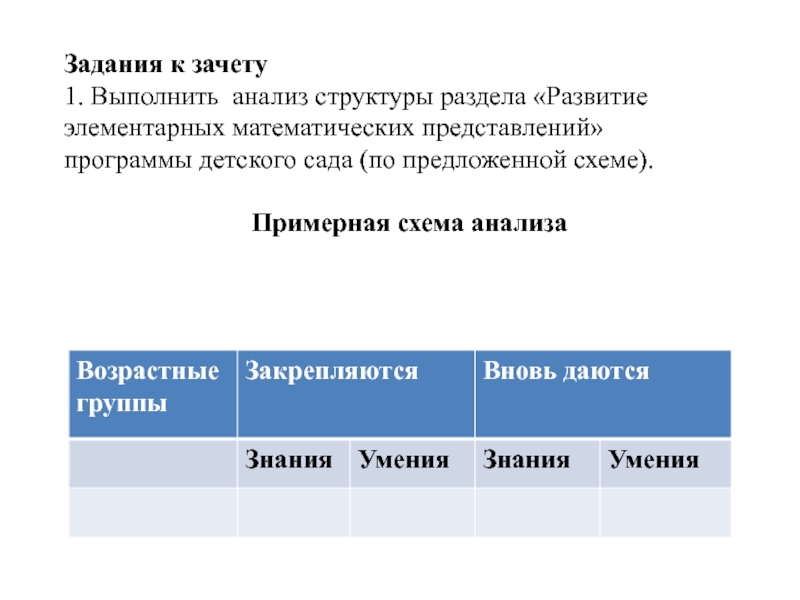
Слайд 113Задания к зачету
1. Выполнить анализ структуры раздела «Развитие элементарных математических
представлений»
программы детского сада (по предложенной схеме).
Примерная схема
анализа
Слайд 1142. Составить библиографический список статей из научно-методических журналов и пособий
(не менее 10 наименований) по математическому развитию дошкольников, опубликованных за
последние 5 лет.
Написать аннотацию к одной из статей по плану:
- название, автор, выходные данные;
- какие вопросы поднимает автор;
- какое практическое значение имеет данный материал для воспитателя.
Слайд 115Развитие у детей представлений о множестве
Ключевые слова: восприятие и
отображение множеств детьми раннего и дошкольного возраста, количественный счет, порядковый
счет, этапы обучения счетной деятельности.
Познание количества, количественных отношений осуществляется детьми в основном в наглядно-образной форме, в процессе предметной деятельности.
Ребенок имеет дело с конкретными количествами предметов (например, различного вида игрушками). Он выделяет из группы отдельный предмет (выбирает один карандаш из всех находящихся в коробке, одну машину из всех стоящих в игровом уголке), объединяет предметы (складывает кубики в ящик, надевает на стержень колечки пирамидки), отделяет часть от других предметов (из всего строительного материала берет только кирпичики, чтобы ставить забор).
Действуя с предметами, ребенок сравнивает их количество и сообщает об этом: «Вот у меня сколько!», «А у меня больше!».
Слайд 116Исследования А. М. Леушиной показали, что сначала учить детей надо
не числу, а сравнению (способствовать формированию у них представлений о
количественных отношениях), а затем уже знакомить со счетной деятельностью, пользуясь числительными.
Представления о совокупностях формируются у детей благодаря накоплению однородных восприятий: слуховых, двигательных, зрительных.
Ребенок первого года жизни реагирует на множество иначе, чем на один предмет: он замечает большое количество однородных предметов. Он рано начинает отличать один предмет от группы предметов и употреблять существительные во множественном числе.
Развитие у детей представлений о множестве
Слайд 117Например, игры с куклами. Взрослый просит ребят собрать всех кукол
вместе, затем отобрать самых маленьких из них. Позже малыши получают
следующее задание: посадить рядом кукол в платочках и т. д.
Как видим, куклы разделены на группы по размеру, наличию головных уборов, цвету одежды. Если дети умеют произвести такой анализ, их можно научить сравнению: каких кукол много (маленьких или больших), каких мало или поровну.
Работа со множествами заключается в умении практически установить взаимно однозначное соответствие между элементами двух групп и определить их равенство и неравенство.
Развитие у детей представлений о множестве
Слайд 118
Развитие у детей представлений о множестве
Слайд 119Организуя обучение детей, следует:
-приучать дошкольников наблюдать за действиями взрослых
с предметами, слушать, как словами характеризуются эти действия;
- учить
их действовать и сопровождать действия словами;
побуждать детей повторять за взрослыми сказанное о свойствах, качествах предметов.
Чтобы восприятие было более полным, в нем должно участвовать одновременно несколько анализаторов, т. е. ребенок должен не только видеть и слышать, но и действовать с предметами — ощупывать, производить различные движения.
Развитие у детей представлений о множестве
Слайд 120Воспитатель должен иметь в виду, что простейшее представление о количестве
можно дать детям лишь в том случае, если в достаточной
степени развиты речь и восприятие.
При проведении игры или специального упражнения детей объединяют в подгруппы из 6 — 8 человек. В одной подгруппе должны быть обязательно и активные, и пассивные дети.
Игры, упражнения должны занимать не более 8—10 мин.
Формы обучения малыша, основанные на использовании его способности к наблюдению и подражанию, обязательно включают в себя элемент заинтересованности .
Развитие у детей представлений о множестве
Слайд 121К 3 годам активный словарь ребенка включает более чем 1300—1400
слов.
Как правило, называют слова-числительные в беспорядке (один, три, восемь,
пять), хотя иногда и в общепринятой последовательности (один, два, три, четыре). Однако это еще не означает, что они овладели счетом, и не дает основания делать вывод об их математических способностях (А.М. Леушина).
Очень часто дети начинают раньше понимать и использовать слово-числительное два, нежели один. Количество одноэлементного множества, как правило, не обозначается и взрослыми, а называется: не одна кукла, а просто кукла.
Развитие представления о числе
Слайд 122 Ребенок становится свидетелем того, как взрослые считают разные предметы: «Принеси
две конфеты», «Дай второй ботинок». Это способствует усвоению детьми количественных
отношений с помощью соответствующих слов.
Лучше всего они овладевают теми словами-числительными, которые используются непосредственно в процессе практических действий ребенка.
Во время обучения детей счету следует учитывать раннее усвоение (заимствование) числительных из речи взрослых.
Однако не следует начинать обучение счету с усвоения числительных. Этому должны предшествовать практические действия с множествами (игрушками).
Развитие представления о числе
Слайд 123Этапы формирования количественных представлений.
Дочисловой этап и обучение счету
Слайд 129После усвоения счета предметов дети считают другие объекты:
Счет звуков. Дети
считают до 5 звуков. Рекомендуется использовать: барабан, металлофон, пианино, камертон,
дудку, стук, хлопки, топот. Задания: посчитай, сколько звуков. Отсчитай столько же предметов. Сколько отложил? Почему столько? Проверь, пересчитай.
Счет на ощупь. В качестве материала используются объемные предметы, знакомые детям (кубики, пуговицы, камешки, желуди и т.п.). Счетные карточки с пуговицами или дырочками в чехлах плотной ткани. Чехлы снимаются.
Счет движений. Используются простые, доступные детям виды движений: прыжки, приседания, наклоны и др. Задания: по названному числу, по образцу, счет движений комбинируется со счетом звуков и на ощупь.
Слайд 130Независимость числа от формы расположения предметов и расстояния между предметами.
После обучения счету детей знакомят с независимостью числа от размеров
предметов и их пространственного расположения.
Дети должны понять, что число – это абстрактное математическое понятие – количественная характеристика множества.
Одинаковые предметы двух контрастных размеров располагаем так, чтобы не прослеживалось приложение и действительно казалось, что одних предметов больше. А других – меньше. Используя приемы наложения и приложения, дети убеждаются в том, что хотя одни предметы большие, а другие маленькие, их поровну, одинаковое количество. Число не зависит от размеров предметов.
Слайд 135Методика формирования умения решать и
составлять арифметические задачи
Арифметические задачи (решаются арифметическим
действием).
Текстовые задачи (сформулированы на естественном языке).
Простые задачи (в одно действие).
Составные задачи (в несколько действий).
Прямые задачи (вопрос подсказывает
действие).
Обратные (косвенные) задачи (вопрос не отражает явно ситуацию)
Предварительная работа
Практическая работа с множествами и числами является основой для обучения детей умению решать и составлять арифметические задачи.
Особенности наглядного материала
В процессе обучения дошкольников умению решать и составлять арифметические задачи применяем различные модели: вещественные (предметы и их заменители), графические (рисунки, схемы), словесные и математические (числовые выражения).
Слайд 136Методика формирования умения решать и
составлять арифметические задачи
По характеру наглядности
задачи делятся на:
1. Задачи-драматизации (сюжет и действия разыгрывают сами дети: “Петя, поставь
3 флажка в вазу. Маша, поставь 2 флажка в вазу. Дети, про это можно придумать задачу”).
2. Задачи-иллюстрации (условие изображается на картинках):
а) картинки, обеспечивающие предметную наглядность (предметы и действия ярко выражены: в вазе лежат 3 яблока, девочка кладет еще 2 яблока);
б) парные картинки (на левой – 3 лягушки на кочке, на правой – 2 лягушки на кочке, а 1 лягушка плавает);
в) картинки, обеспечивающие частичную наглядность (3 снежные бабы и 2 лужи);
г) картинки, отражающие только жизненную ситуацию (на верхней полке 4 книги, а на нижней – 3 книги).
3. Устные задачи (без наглядности).
Слайд 137Методика формирования умения решать и
составлять арифметические задачи
При обучении дошкольников
часто используются различные задачи, отражающие знакомые детям ситуации, но специальная
работа ведется в подготовительной группе.
В начале используем простые прямые задачи, где в решении второе слагаемое и вычитаемое равны единице.
При прочном знании состава числа из двух меньших используем любые числа в пределах десятка. Затем при хорошем усвоении можно предложить косвенные задачи.
Слайд 138Методика формирования умения решать и составлять арифметические задачи
Этапы обучения:
Подготовительный этап:
Работа
с множествами, их объединение и разъединение, знакомство с понятиями “часть
и целое”.
I этап:
Ознакомление с понятием “арифметическая задача”:
а) формирование представления об арифметической задаче;
б) усвоение структуры задачи и выделение ее частей;
в) практическое составление задач;
г) полная формулировка ответа.
II этап:
Запись и формулировка решения задачи:
а) знакомство с арифметическими действиями: сложением и вычитанием;
б) поиск нужного арифметического действия и его формулировка;
в) выкладывание решения задачи с помощью карточек;
г) запись решения задачи на листе бумаги в клетку.
III этап:
Выработка вычислительных навыков и логических рассуждений:
а) присчитывание и отсчитывание по единице;
б) применение знания состава числа из двух меньших чисел;
в) использование моделей арифметических действий;
г) решение косвенных задач, логических задач и др.
Слайд 139Особенности и методика формирования и развития у дошкольников представлений о
размерах предметов
Величина — это и протяженность, и объем, и
скорость, и масса, и число, и т.д.
Величина является свойством предмета, воспринимаемым различными анализаторами: зрительным, тактильным и двигательным.
Величина предмета, т.е. размер предмета, определяется только на основе сравнения.
Восприятие величины зависит от расстояния, с которого предмет воспринимается, а также от величины предмета, с которым он сравнивается.
Характеристика величины предмета зависит также от расположения его в пространстве.
Величина конкретного предмета характеризуется такими особенностями: сравнимость, изменчивость и относительность.
Слайд 140Величины, с которыми знакомятся дошкольники
Длина – это характеристика линейных
размеров предметов. Длины любых предметов можно сравнивать на глаз, приложением
или наложением. При этом всегда можно либо приблизительно, либо точно определить, на сколько одна длина больше (меньше) другой.
Масса - это физическое свойство предмета, измеряемое с помощью взвешивания. Следует различать массу и вес предмета. Чтобы ребенок усвоил правильную терминологию, следует всегда говорить: «масса предмета».
Кроме взвешивания массу можно приблизительно определить прикидкой на руке («барическое чувство»).
Емкость - это объем мер жидкости
Площадь – это свойство фигуры занимать определенное место на плоскости.
Время - это длительность протекания процессов
Скорость – это путь, пройденный телом за единицу времени. Скорость – величина физическая, ее наименование содержит 2 величины: единицы длины и единицы времени: 3км/час, 45м/сек и т.п.
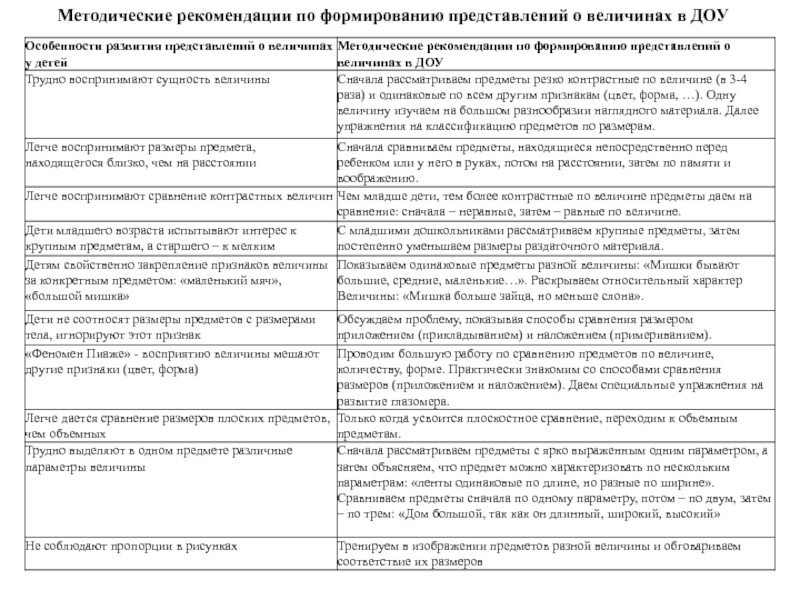
Слайд 141Методические рекомендации по формированию представлений о величинах в ДОУ
Слайд 142Дошкольники знакомятся:
• с плоскими геометрическими фигурами: точкой, различными линиями (обычно
в процессе изобразительной деятельности), квадратом, кругом, треугольником, прямоугольником, овалом;
• обобщающими
понятиями: четырехугольником, многоугольником;
• объемными фигурами (телами): шаром, кубом, цилиндром, параллелепипедом, конусом, пирамидой, призмой (часто используются предэталонные названия: “кирпичик”, “крыша” и др.).
Необходимо обучать детей:
• правильным приемам обследования формы;
• развивать способность выявлять простейшие свойства фигур;
• учить выбирать по образцу и слову предметы и фигуры;
• группировать предметы и фигуры по признаку формы;
• определять форму окружающих предметов;
• видоизменять фигуры;
• создавать модели предметов из геометрических фигур.
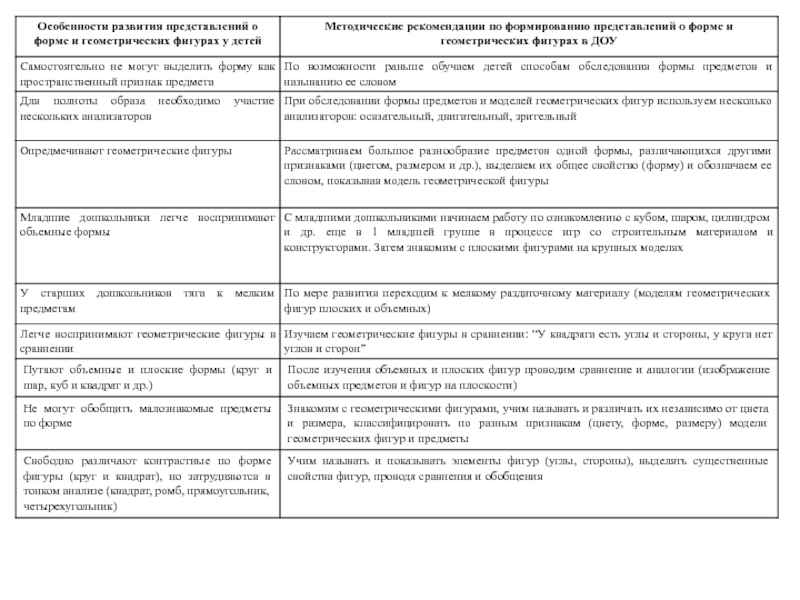
Особенности формирования и развития у дошкольников представлений о форме предметов и геометрических фигурах
Слайд 143Особенности формирования и развития у дошкольников представлений о форме предметов
и геометрических фигурах
Механизмы восприятия формы:
Ранний возраст: хватание предметов и манипуляция с
ними.
Второй год жизни: обследование предмета (направленные действия).
Третий-четвертый годы жизни: ощупывательные движения ладошкой, взгляд падает по центру предмета (для обследования формы используем осязательно-двигательный путь).
Пятый-шестой годы жизни: ощупывают предмет обеими руками.
К семи годам: последовательно прослеживают кончиками пальцев весь контур фигуры, обследуют контур предмета глазами.
Первичное познание формы предметов осуществляется в процессе действия с ним (узнавание бутылочки с молоком).
В конце второго года жизни появляются зрительные реакции определения формы предмета, которые предшествуют практическим действиям.
Дети третьего года жизни, прежде чем действовать, подробно зрительно и осязательно-двигательно знакомятся с предметом. У них возникает интерес к форме предметов, что необходимо использовать в обучении и познакомить детей с эталонами (геометрическими фигурами).

Слайд 144Особенности формирования и развития у дошкольников представлений о форме предметов
и геометрических фигурах
Этапы восприятия формы:
I. (3-4 года). Узнавание предметов по
форме (выделение формы как существенного признака).
II. (4-5 лет). Знакомство с эталонами (распознавание, называние геометрических фигур и некоторых их свойств).
III. (5-6 лет). Умение определять форму предметов и их частей, составлять из геометрических фигур модели различных предметов, выявлять свойства, связи и отношения геометрических фигур.
Проблему знакомства детей с геометрическими фигурами и их свойствами следует рассматривать в двух аспектах:
• в плане сенсорного восприятия и использования как эталонов в познании форм окружающих предметов;
• в смысле познания особенностей структуры фигур, их свойств, основных связей, отношений, закономерностей в их построении (т. е. собственно геометрического материала).
Слайд 145Особенности формирования и развития у дошкольников представлений о форме предметов
и геометрических фигурах
Этапы восприятия геометрических фигур:
В начале дети воспринимают геометрические фигуры
как игрушки (называют их именами предметов: цилиндр – стаканом, столбиком, треугольник – крышей и т. п.).
II. В процессе обучения дети перестраиваются и уже не отождествляют, а сравнивают фигуры с предметами (цилиндр – как стакан, шар похож на мячик и т. п.).
III. Воспринимают геометрические фигуры как эталоны (платок квадратный, пуговица круглая и т. д.).
Задачей сенсорного развития является формирование у ребенка умения узнавать форму различных предметов и соотносить ее с эталоном. (Л.А. Венгер).
В дальнейшем необходимо сосредотачивать внимание детей на осмыслении и анализе свойств геометрических фигур (Т. Игнатьева).
Слайд 146Особенности формирования и развития у дошкольников представлений о форме предметов
и геометрических фигурах
Этапы восприятия свойств геометрических фигур:
I. Фигура воспринимается как
целое. Ребенок не выделяет в ней отдельные элементы (углы, стороны), не замечает сходства и различия.
II. Ребенок выделяет в фигуре ее элементы, устанавливает отношения между ними (у квадрата все стороны равны по длине).
III. Ребенок в состоянии установить связи между свойствами и структурой фигуры (у большого квадрата стороны длиннее, чем у маленького).
Переход от одного уровня к другому протекает не самопроизвольно, а под влиянием целенаправленного обучения (А.М. Пышкало, А.А. Столяр). Отсутствие обучения тормозит развитие.
Слайд 147Особенности формирования и развития у дошкольников представлений о форме предметов
и геометрических фигурах
Последовательность в формировании представлений о геометрических фигурах
1.
Демонстрация геометрической фигуры и называние ее.
2. Обследование геометрической фигуры путем конкретных практических действий.
3. Показ еще нескольких таких же геометрических фигур, но разных и по цвету и величине.
4. Сравнение геометрических фигур с предметами, близкими по форме; нахождение среди окружающих предметов таких, которые близки по своей форме с этой фигурой.
5. Сравнение предметов по форме между собой с использованием геометрический фигур как эталона.
6. Сравнение знакомых геометрических фигур, определение общих качеств и различий (овал и круг, квадрат и прямоугольник и т.д. ).
7. Закрепление свойств геометрических фигур с помощью измерения, лепки, рисования, выкладывания, построения и др.
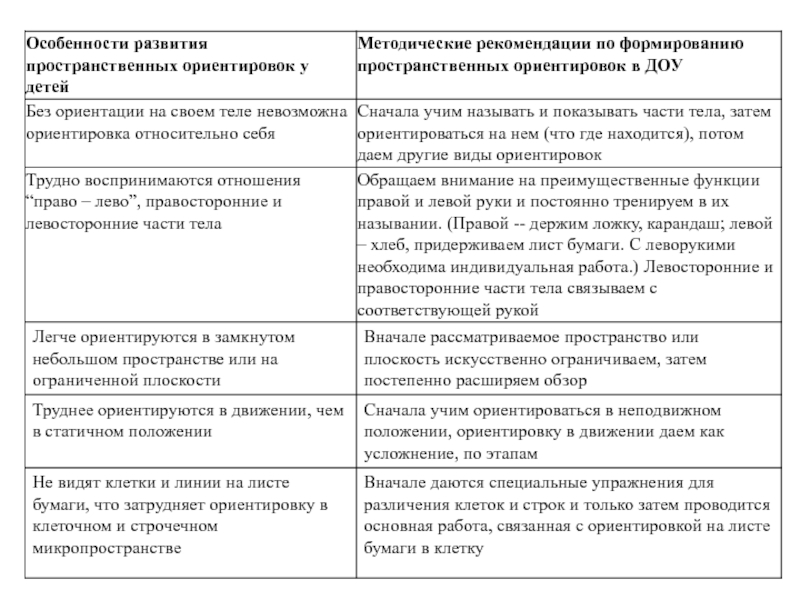
Слайд 149Особенности и методика формирования и развития пространственных представлений у дошкольников
В понятие пространственной ориентации входит оценка расстояний, размеров, формы, взаимного
положения предметов и их положения относительно ориентирующегося.
Пространственная ориентировка осуществляется на основе непосредственного восприятия пространства и словесного обозначения пространственных категорий (местоположения, удаленности, пространственных отношений между предметами).
В более узком значении выражение “пространственная ориентировка” имеет в виду ориентировку на местности:
• определение “точки стояния” (“Я нахожусь справа от дома”);
• определение местонахождения объектов относительно ориентирующегося (“Шкаф находится слева от меня”);
• определение расположения предметов относительно друг друга (“Мяч лежит под столом”).
При передвижении человека пространственная ориентировка происходит постоянно:
• постановка цели и выбор маршрута движения (направление);
• сохранение направления движения и достижение цели.
Слайд 150Особенности и методика формирования и развития пространственных представлений у дошкольников
В период раннего детства ребенок ориентируется в пространстве на основе чувственной
системы отсчета (по сторонам собственного тела).
В дошкольном возрасте ребенок овладевает словесной системой отсчета по основным пространственным направлениям: вперед – назад, вверх – вниз, направо – налево.
В школьные годы дети овладевают новой системой отсчета – по сторонам горизонта: север, юг, запад, восток.
Система работы (предложенная Т.А. Мусейибовой) по развитию у дошкольников пространственных представлений включает:
1) ориентировку “на себе” (знание собственного тела);
2) ориентировку “на внешних объектах” (выделение различных сторон предметов: передней, тыльной, верхней, нижней, боковой);
3) освоение и применение словесной системы отсчета по основным направлениям: вперед – назад, вверх – вниз, направо – налево;
4) определение расположения предметов в пространстве “от себя”;
5) определение собственного положения в пространстве;
6) определение пространственного размещения предметов относительно друг друга;
7) определение расположения предметов на плоскости.

Слайд 151Особенности и методика формирования и развития пространственных представлений у дошкольников
Этапы восприятия пространственных отношений между предметами:
I этап: Пространственные отношения не выделяются
ребенком. Окружающие предметы воспринимаются отдельно без пространственной взаимосвязи.
II этап: Практическое примеривание. (Контактная близость.) Ребенок прислоняется спиной: “Шкаф сзади”; дотрагивается рукой: “Стол справа”. При расположении предметов в ряд или по кругу дети плотно прижимают их друг к другу.
III этап: Зрительная оценка. Прием контактной близости заменяется поворотом корпуса, потом указательным движением руки, далее легким движением головы и, наконец, взглядом. Большую роль играет слово.
Практические действия постепенно сворачиваются и переходят в умственные.
В 3 года у детей появляется возможность зрительной оценки расположения объектов на ограниченном пространстве. В 5 лет возрастает степень удаленности предметов.
Выводы:
Дошкольный возраст – это период освоения словесной системой отсчета по основным пространственным направлениям.
Ориентировка на собственном теле служит исходной в освоении ребенком пространственных направлений.
При обучении необходимо формировать взаимно обратные пространственные отношения одновременно.

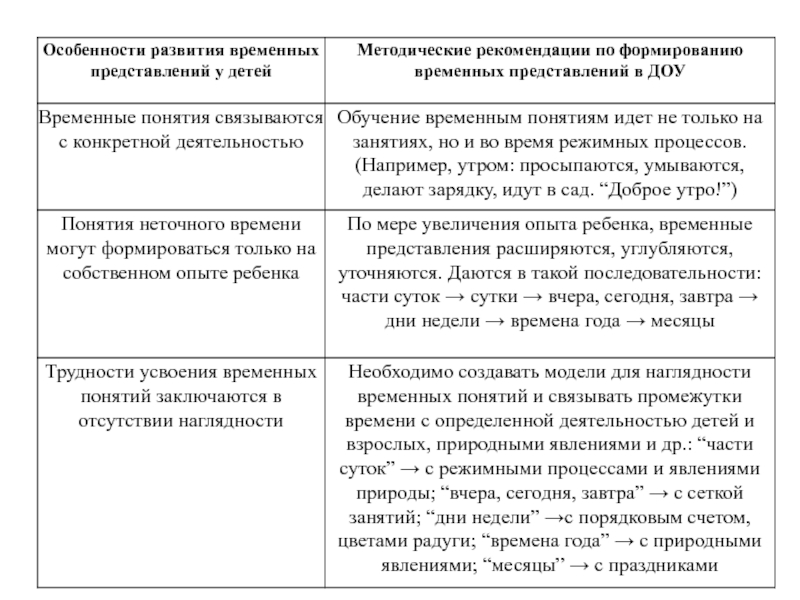
Слайд 153Особенности и методика формирования и развития
представлений о времени у
дошкольников
Слово «время» происходит от древнерусского «веремя», что означает «вращение».
Особенности времени:
• текучесть (нельзя остановить);
• необратимость (нельзя повернуть вспять);
• непрерывность (нельзя разбить на отдельные элементы);
• отсутствие наглядности (вызывает основные трудности у детей).
Окружающий нас мир существует во времени. Временными характеристиками природных явлений являются:
продолжительность, последовательность, частота, ритм, темп.
Промежутки времени измеряют.
Единицей времени выбирается регулярно повторяющийся процесс. Такие единицы времени, как год, сутки, были взяты из природы, а час, минута, секунда придуманы человеком. Все меры времени (секунда, минута, час, сутки, неделя, месяц, год) представляют систему временных эталонов, где каждая мера складывается из единиц предыдущей.
Слайд 154Особенности и методика формирования и развития
представлений о времени у
дошкольников
Факторы, формирующие чувство времени:
- знание временных эталонов;
-
переживание - чувствование детьми длительности временных интервалов в деятельности;
- развитие у детей умения оценивать временные интервалы без часов, на основе чувства времени.
Этапы организации работы:
- учить определять окончание срока выполнения деятельности по песочным часам (задание, сделать за 1 минуту лодочку);
- учить оценивать по представлению длительность интервала времени в процессе деятельности (за 3 минуты);
- учить предварительно планировать объем деятельности на указанный отрезок времени на основе имеющегося представления о его длительности (проверку намеченного объема работы по песочным часам);
- учить переносить умения оценивать длительность временных отрезков в жизнь
Слайд 155Особенности и методика формирования и развития
представлений о времени у
дошкольников
В младшей группе дети способны воспринять такие промежутки времени,
как части суток (утро, день, вечер, ночь), связывая их со своей деятельностью.
В средней группе необходимо углубить и расширить эти знания и дать понятия “вчера, сегодня, завтра”.
В старшей и подготовительной группах знакомим детей с днями недели, временами и месяцами года, с календарем.
Учат пользоваться в речи словами-понятиями: сначала, потом до, после, раньше, позже, в одно и то же время.
Детей можно познакомить с интервалами в 1, 2, 3, 5, 10 минут, полчаса, час; научить пользоваться часами (песочными и механическими), секундомером.
Слайд 156Особенности и методика формирования и развития
представлений о времени у
дошкольников
Значение развития временных представлений у дошкольников
Детям уже в раннем
возрасте жизненно необходимо научиться самим ориентироваться во времени:
• планировать деятельность во времени (сначала – потом);
• менять темп (быстро – медленно) и ритм (часто – редко) своих действий в зависимости от наличия времени;
• правильно обозначать в речи временные понятия;
• определять время по часам;
• измерять временные промежутки и др.
Умение регулировать и планировать деятельность во времени создает основу для развития таких качеств личности, как организованность, собранность, целенаправленность, точность, что необходимо ребенку в повседневной жизни и при обучении в школе.
Слайд 157Особенности и методика формирования и развития
представлений о времени у
дошкольников
Н.И. Красногорский подчеркивал необходимость развития у детей “чувства времени”.
С.Л.
Рубинштейн обращала внимание на то, что на правильную оценку длительности времени оказывают три фактора:
• содержание деятельности;
• интерес к деятельности;
• возраст детей.
Ю.Д. Фаусек рекомендовала проводить “уроки тишины” (предложить детям 1 минуту посидеть тихо, закрыв глаза).
Т. Д. Рихтерман предложила систему работы по формированию умения ориентироваться во времени, придавала большое значение выработке “установки на время” (не опоздать, уложиться), чтобы дисциплинировать детей.
Слайд 159Предметно-развивающая среда как условие эффективного математического развития ребенка.
Под развивающей
предметно-пространственной средой следует понимать естественную комфортабельную обстановку, рационально организованную в
пространстве и времени, насыщенную разнообразными предметами и игровыми материалами.
Предметно-пространственная развивающая среда включает в себя три компонента: предметное содержание, его пространственную организацию и их изменения во времени.
К предметному содержанию относятся:
игры, предметы и игровые материалы, с которыми ребенок действует преимущественно самостоятельно или в совместной со взрослым и сверстниками деятельности (например, геометрический конструктор, пазлы);
учебно-методические пособия, модели, используемые взрослым в процессе обучения детей (например, числовая лесенка, обучающие книги);
оборудование для осуществления детьми разнообразных деятельностей (например, материалы для экспериментирования, измерений).
Слайд 160Требования к наглядному материалу :
-предметы для счета и их
изображения должны быть известны детям, они берутся из окружающей жизни;
-чтобы научить детей сравнивать количества в разных совокупностях, необходимо разнообразить дидактический материал, который можно было бы воспринимать разными органами чувств (на слух, зрительно, на ощупь);
-наглядный материал должен быть динамичным и в достаточном количестве; отвечать гигиеническим, педагогическим и эстетическим требованиям.
Требования к методике использования наглядного материала:
При подготовке к занятию тщательно продумать, когда (в какой части занятия), в какой деятельности и как будет использован данный наглядный материал.
Необходимо правильно дозировать наглядный материал. Негативно сказывается на результатах обучения как недостаточное его использование, так и излишки.
Наглядность не должна использоваться только для активизации внимания. Это слишком узкая цель.
Слайд 161Для каждой возрастной группы имеется свой комплект наглядного материала.
Это
—комплексное дидактическое средство, обеспечивающее формирование элементарных математических представлений в условиях
целенаправленного обучения на занятиях. Благодаря ему возможно решение практически всех программных задач.
Наглядный дидактический материал рассчитан на определенное содержание, методы, фронтальные формы организации обучения, соответствует возрастным особенностям детей, отвечает разнообразным требованиям: научным, педагогическим, эстетическим, санитарно-гигиеническим, экономическим и т. д. Он используется на занятиях при объяснении нового, его закреплении, для повторения пройденного и при проверке знаний детей, т. е. на всех этапах обучения.
Слайд 162Мария Фидлер Математика уже в детском саду : Пособие для воспитателя дет.
сада ;
Перевод с польского О. А. Павлович
М. Просвещение 1981
Слайд 163Примеры, рассмотренные в книге, подтверждают возможность проведения самой разнообразной работы
как с младшими детьми (трех и четырех лет), так и
со старшими (пяти и шести лет) с целью:
а) развития умения выделять различные качественные признаки предметов и их множеств; умения выявлять качественные соотношения, как предметов, так и множеств предметов;
б) развития представления о числе предметов и о количественных соотношениях, существующих между множествами; выработки навыков выполнения элементарных действий, связанных с числами: расчленение множеств на непересекающиеся подмножества, прибавление и вычитание чисел в объеме, предусматриваемом программой.
Это в основном примеры применения методов обучения, связанных с действием, с движением. Здесь продемонстрированы богатые возможности, позволяющие путем постановки специальных заданий, путем ненавязчивого принуждения ребенка к многократному выполнению различных действий (сравнения, упорядочения, установления соответствия между элементами множеств) стимулировать его самостоятельную деятельность, направить ее в нужном направлении. Имеются здесь и примеры использования словесных методов: бесед, рассказов, загадок, а также примеры наглядных методов обучения.

Слайд 164ДЕТИ МЛАДШЕГО ВОЗРАСТА — ТРЕХ - И ЧЕТЫРЕХЛЕТНИЕ
КЛАССИФИКАЦИЯ ПРЕДМЕТОВ ПО
РАЗЛИЧНЫМ ПРИЗНАКАМ
(«принадлежит к...» или «не принадлежит к...»)
После дождя четырехлетние дети
вышли на прогулку в парк.
На дорожках были лужи. Кто-то из мальчиков бросил в воду камешек. Камешек утонул. Началось бросание. Детям было интересно узнать, каждый ли камешек утонет. Тонули даже самые маленькие.
Тогда воспитательница предложила Вальдеку бросить в воду шишку, которая была больше камня. И вдруг оказалось, что шишка не утонула. И другие шишки плавали на поверхности лужи. Почему?
А потому, что камень тяжелее шишки, — ответил кто-то.
Ну нет, моя шишка больше всех. Она такая большая, а камень такой маленький. Но и она не утонула, — резко запротестовала Зося.
Прутик Юрека тоже не утонул. Почему? — На этот раз вопрос остался без ответа, но разделение предметов на те, которые тонут, и те, которые не тонут, было замечено детьми.
Слайд 165Дидактический материал по формированию элементарных математических представлений для детей 3–4
лет
«Собери неваляшку»
Есть у нас одна игрушка
Не машинка, не зверюшка.
Положить
нельзя милашку –
Она зовется Неваляшка.
Наша добрая и любимая игрушка
- Неваляшка, которой уже около 200 лет, а она не стареет и не исчезает из детской игровой жизни.
В дошкольном воспитании Неваляшка помогает в разных видах детской деятельности. В режимных и сюрпризных моментах, неваляшка поможет, подскажет и поиграет с детьми. В продуктивной деятельности для Неваляшки можно построить дом, нарисовать или слепить подружек. А нам Неваляшка поможет при обучении детей элементарным математическим представлениям.
Слайд 166Этот дидактический материал приготовлен из картона (для более практичности можно
заламинировать, с помощью которого решаются сразу несколько задач :
продолжать учить
счету в пределах 4;
закреплять умение сравнивать две группы предметов, отвечать на вопросы чего больше (меньше) ;
расширять представления о том, что результат счета не зависит от качественных признаков предмета;
упражнять в умение сравнивать предметы по величине;
продолжать учить сравнивать две группы предметов путем наложения и приложения, находить одинаковые;
раскладывать в убывающей и возрастающей последовательности;
подвести к пониманию, что результат счета не зависит от величины предметов;
упражнять в определении расположения предметов (впереди, сзади, справа, слева).
Слайд 167Задание:
Собрать из предложенных фигур неваляшку
Какой формы фигуры, из которых собрали
неваляшку?
Сколько кругов?
Какого цвета круги?
Все круги одинакового цвета?
Одинакового ли размера круги?
Как
узнать, что круги разные?
Задание:
Наложите круги друг на друга.
Найдите самый большой круг.
Найдите самый маленький круг.
Есть ли круги одинакового размера?
Одинаковые круги большие, средние или маленькие?
Сколько маленьких кругов?
Сколько всего кругов?
Каких кругов больше больших или средних?
Каких кругов больше больших или маленьких?
Слайд 168
Задание:
Под каждый большой круг приложите маленький.
Каких кругов больше?
Сколько всего будет
кругов, если убрать один маленький?
Задание:
Разложите три круга в порядке от
самого большого к самому маленькому.
Разложите три круга в порядке от самого маленького к самому большому.
Какого размера круг посередине?
Какого размера круг справа (слева)
Задание:
Положите перед собой один маленький круг, снизу положите
самый большой, а сверху средний.
Сколько перед вами кругов?
Задание:
Соберите неваляшку.
Что еще может быть круглым у неваляшки?
Слайд 169"Счетные палочки Кюизенера»
Что представляют собой палочки Кюизенера?
Каждая палочка Кюизенера символизирует
число от 1 до 10. Они отличаются по длине (от
1 до 10 см соответственно), а также по цвету. Цвета для каждого числа подобраны не случайно, они собраны в определенные блоки:
2, 4, 8 - оттенки красного (элементы длиной 2 см - розового цвета, 4 см - коричневого или красного, а 8 см - вишневого или темно-бордового);
3, 6, 9 - зеленый и синий (3 см - светло-зеленый или голубой, 6 см - зеленый или фиолетовый, 9 см - синий);
5, 10 - оттенки желтого (элементы длиной 5 см - желтого цвета, а длиной 10 см - оранжевого).
Маленькие палочки-кубики, которые символизируют число 1 (длиной и шириной 1 см), просто белые, их в наборе больше других.
Число 7, которое также стоит особняком, обрело нейтральный черный цвет.
еще называют "универсальными цветными числами" или "цветными линейками". Придумал пособие учитель младших классов из Бельгии Джордж Кюизенер в далеком 1952 году. Это великолепный материал для обучения и развития интеллектуальных способностей ребенка от 1,5 до 7 лет.
Слайд 170Занятия начинаются с простых и понятных малышу игр (подбираем детали
по длине и цвету, складываем пирамидку от большого к маленькому
и наоборот, ищем деталь длиннее или короче, складываем паровозики, дорожки и т.д.). Даже складывание этих цветных линеечек в коробку уже является непростой и увлекательной задачей для маленького ребенка. Нужно подобрать каждой палочке свой "домик", правильно собрать их вместе.
Со временем занятия усложняются, игровой этап переходит в математическое обучение.
Дети учатся основам счета (белый кубик - один, а на других палочках таких кубиков поместится много), они изучают состав каждого числа, учатся находить нужные палочки по цвету и длине, создают картинки из разного количества деталей и др.
Палочки Кюизенера развивают и другие навыки: мелкую моторику рук, творческий потенциал, пространственное восприятие. Детали всегда нужно собирать в их коробочку, это приучает ребенка к порядку и дисциплине.
Слайд 171Логические блоки Дьенеша
Логические блоки придумал венгерский математик и психолог Золтан
Дьенеш. Игры с блоками доступно, на наглядной основе знакомят детей
с формой, цветом, размером и толщиной объектов, с математическими представлениями и начальными знаниями по информатике. Развивают у детей мыслительные операции (анализ, сравнение, классификация, обобщение), логическое мышление, творческие способности и познавательные
Логические блоки Дьенеша представляют собой набор из 48 геометрических фигур:
а) четырех форм (круги, треугольники, квадраты, прямоугольники);
б) трех цветов (красные, синие и желтые);
в) двух размеров (большие и маленькие);
г) двух видов толщины (толстые и тонкие).
В наборе нет ни одной одинаковой фигуры. Каждая геометрическая фигура характеризуется четырьмя признаками: формой, цветом, размером, толщиной.
Слайд 172Первое знакомство с геометрическими фигурами Дьенеша
Воспитательница сказала детям, что принесла
новые кубики, каких у них еще не было. Она поставила
четыре столика и высыпала на середину каждого из них разноцветные геометрические фигурки, предварительно рассортированные по форме:
на один стол — круги, на второй — треугольники, на третий — квадраты, на четвертый — прямоугольники.
Воспитательница дает ребятам время на изучение свойств геометрических фигур и на дальнейшую самостоятельную классификацию их по признакам величины и толщины.
Слайд 173Каждая пара распределяет свои геометрические фигуры так, чтобы было видно,
что одни из них — большие, а другие—маленькие, что одни
— толстые, а другие — тонкие.
Перед каждой парой детей имеется только одна геометрическая фигура (или круг, или треугольник, или квадрат, или прямоугольник), которая будет и большой и толстой или и большой и тонкой; только одна геометрическая фигура определенного вида, которая будет и маленькой и толстой или и маленькой и тонкой.
Среди желтых кругов имеются два больших круга, один из которых толстый, а другой — тонкий.
На другом столе лежат красные квадраты, но только один из них большой и толстый и только один большой и тонкий, только один маленький и толстый, только один маленький и тонкий.
Слайд 175В следующий раз игра проводилась по-другому: ребенок, видя перед собой
какую-либо геометрическую фигуру, должен был перечислить четыре ее признака: форму,
величину, толщину и цвет. Сначала каждый из детей по очереди называл признаки своей геометрической фигуры, например:
У меня квадрат, большой, толстый, голубой.
У меня круг, красный, маленький, толстый.
У меня треугольник, желтый, тонкий, большой.
Слайд 176Большое познавательное значение имеет складывание из геометрических фигур Дьенеша домиков,
машинок, башен, скворечников и т. п. В процессе постройки дети
убеждаются, что во всем комплекте нет двух совершенно одинаковых геометрических фигур: если, например, геометрическая фигура является, голубым толстым большим кругом, то все другие большие круги или не будут толстые, или будут толстые, но другого цвета; если нужен маленький тонкий голубой треугольник, то он будет только один, другого голубого не найдется среди маленьких тонких треугольников
Слайд 177Для проверки того, насколько хорошо дети усвоили признаки геометрических фигур,
был введен специальный код, графически изображающий эти признаки с помощью
рисунков. С этой целью воспитательница использовала код, предложенный для дошкольников профессором Семадени
Слайд 178Для детей это что-то совершенно новое. Они удивляются тому, что
могут «прочитать», какой является выбранная геометрическая фигура.
Слайд 179Что умеют счетные палочки?
1)Задачи на построение простых фигур;
2)Задачи на построение
сложных фигур;
3)Задачи на преобразование фигур
(головоломки- добавь/убери палочки)
Слайд 180Сфинкс
В состав относительно несложной головоломки "Сфинкс" входит семь простых
геометрических фигур: четыре треугольника и три четырехугольника с разным соотношением
сторон. Игра развивает восприятие формы, способность выделять фигуру из фона, выделение основных признаков объекта, глазомер, воображение (репродуктивное и творческое), зрительно-моторную координацию, зрительный анализ и синтез, умение работать по правилам.
Слайд 181Танграм
Одна из первых древних игр головоломок. Родина возникновения -
Китай, возраст - более 4 000 лет.
Головоломка представляет собой квадрат
разрезанный на 7 частей: 2 больших треугольника, один средний, 2 маленьких треугольника, квадрат и параллелограмм.
Суть игры - собирать всевозможные фигурки из данных элементов по принципу мозаики. Всего насчитывают более 7 000 различных комбинаций. Самые распространенные из них - фигуры животных и человека.
Игра способствует развитию образного мышления, воображения, комбинаторных способностей, а также умения визуально делить целое на части.
Слайд 182Листик
Геометрическая фигура сложной конфигурации, напоминающая схематичное изображение человеческого сердца
или листа дерева, разделенная на 9 элементов.
Особенно хорошо из
элементов этой головоломки получаются силуэты различных видов транспорта. Полученные изображения напоминают детские рисунки (собачки, птички, человечки). Конструируя простые образные фигуры, дети учатся восприятию формы, способности выделять, фигуру из фона, выделению основных признаков объекта. Головоломка развивает глазомер, аналитико-синтетические функции, воображение (репродуктивное и творческое), зрительно-моторную координацию, умение работать по правилам.
Слайд 183Пентамино
Запатентовал головоломку “Pentomino” Соломон Голомб, житель Балтимора, математик и инженер,
профессор университета Южная Калифорния. Игра состоит из плоских фигур, каждая
из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами, отсюда и название. Существуют еще версия головоломок Тетрамино, состоящие из четырех квадратов, от этой игры и произошел известный Тетрис. Игровой набор “Пентамино” состоит из 12 фигурок. Каждая фигура обозначается латинской буквой, форму которой она напоминает.
Слайд 185 ПЕДАГОГИЧЕСКАЯ ДИАГНОСТИКА
Педагогическая диагностика позволяет:
– установить уровень овладения учебной деятельностью;
– выявить характер трудностей ученика и установить их причины;
–определить особенности
усвоения учащимися предметных знаний, умений и навыков;
– оценить изменения, происходящие в развитии учащихся.
Слайд 186 Первое диагностическое обследование (сентябрь)
Задание 1
Зрительное восприятие
Слайд 187Задание 1
Цель: выявить умение передавать форму фигуры (нарисовать равную или
подобную фигуру, соблюдая пропорции между элементами фигуры).
Кроме того, задание
позволяет судить о твердости руки ребенка, умении рисовать углы, не округляя их, и прямолинейные отрезки.
Текст задания: «Посмотрите сюда (указывается рисунок к заданию). Здесь вы будете выполнять задание. Внутри маленькой рамочки вы видите фигуру. Рассмотрите ее на своих листах. Возьмите карандаш. Нарисуйте похожую фигуру в большой рамочке» (учитель обводит указкой большую рамочку).
Оценка выполнения задания:
0 баллов — не схвачена общая форма фигуры, но изображена какая-либо замкнутая линия.
1 балл — существенно изменены пропорции между элементами фигуры; общая форма фигуры схвачена плохо.
2 балла — изображена подобная или равная фигура, пропорции слегка изменены, но не все углы прямые, не везде соблюдается параллельность линий. Этот же балл ставится, если общая форма фигуры схвачена хорошо, но пропорции между элементами фигуры существенно изменены, однако все углы прямые и параллельность соблюдена.
3 балла — изображена подобная или равная фигура, пропорции между элементами фигуры в основном сохранены.
Если фигура изображена «нетвердой» рукой, в дополнение к баллу ставится знак «минус».

Слайд 188Пространственное восприятие
Выбор и выполнение
арифметических действий
Слайд 189Задание 2
Цель: выявить умение ориентироваться на плоскости (влево, вправо, вверх,
вниз). Проверяется также умение пересчитывать клеточки.
Текст задания: «Задание будете выполнять
на клетчатой части своего листа (указывается место для выполнения задания). Найдите на клетчатом поле чёрную клеточку.
1. Возьмите красный карандаш, отсчитайте от черной клеточки вправо четыре клеточки и пятую закрасьте красным карандашом.
2. Возьмите синий карандаш. От красной клетки отступите вниз на две клеточки и третью закрасьте синим карандашом.
3. Возьмите зеленый карандаш и клеточку, расположенную слева от синей, через одну клеточку от нее, закрасьте зеленым карандашом.
4. Возьмите желтый карандаш. Отсчитайте от зеленой клетки вверх пять клеток и шестую закрасьте желтым карандашом».
Оценка выполнения задания:
0 баллов — не приступил к выполнению задания; несколько клеток закрашены, но их расположение не соответствует инструкции.
1 балл — выполнен верно только один пункт задания, допущены ошибки в направлении, пересчете клеток, начале отсчета.
2 балла — выполнены верно два или три пункта задания.
3 балла — все пункты задания выполнены верно.
Если клетки плохо раскрашены, в дополнение к баллу ставится знак «минус».

Слайд 190Задание 3
Цель: выявить умение выбрать и выполнить операцию сложения и
вычитания; при умение правильно понять текст задачи и перейти от
заданного числа к соответствующему конечному множеству предметов (кружков, квадратов).
Текст задания: «Здесь вы будете выполнять третье задание (указывается место для выполнения задания 3). Посмотрите на свои листы. Послушайте задание.
1. В классе (группе) сегодня дежурят 3 девочки и 2 мальчика. Сколько детей дежурят сегодня в классе? Нарисуйте столько кружков, сколько детей дежурят сегодня в классе. (Текст задачи можно повторить.)
2. В легковой машине ехало 6 человек. Двое вышли из машины. Нарисуйте столько квадратов, сколько человек осталось в машине. (Текст задачи можно повторить.)»
Оценка выполнения задания:
0 баллов — есть попытка решить одну задачу, но число кружков или квадратов неверное.
1 балл — выполнена верно только одна задача, попыток выполнить вторую задачу нет.
2 балла — одна задача выполнена верно, есть попытка решать вторую задачу, но число кружков или квадратов неверное.
3 балла — обе задачи выполнены верно.
Слайд 191Задание 4
Цель: выявить умение сравнивать множества по числу элементов (вне
зависимости от навыка счета).
Текст задания: «Найдите у себя на листках
рисунок, на котором изображены круги и треугольники (указывается рисунок к заданию 4). Чего больше: кругов или треугольников? Если больше кругов, то нарисуйте рядом еще один круг. Если больше треугольников, то нарисуйте еще один треугольник».
Оценка выполнения задания:
0 баллов — сравнение проведено неверно (нарисован один треугольник).
3 балла — сравнение проведено верно (нарисован один круг)
Сравнение множеств
Слайд 192Задание 5
Цель: выявить умение классифицировать, находить признаки, по которым произведена
классификация.
Текст задания: «Рассмотрите эти два рисунка (указываются рисунки к заданию
5). На одном из этих рисунков нужно нарисовать белочку. Подумайте, на каком рисунке вы бы ее нарисовали. От белочки к этому рисунку проведите карандашом линию».
Оценка выполнения задания:
0 баллов — задание не принято, линия не проведена.
3 балла — линия проведена правильно.
Классификация предметов
Слайд 194http://www.maam.ru/obrazovanie/igry-po-matematike
Слайд 195http://ideas4parents.ru/mamina_shkola/matematika.html
Слайд 196Математика- это интересно!
Использованные интернет- ресурсы
Бесплатные настольные игры
www.printplay.ru/
РАЗВИТИЕ РЕБЕНКА
Все для
раннего Развития Детей