Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория игр
Содержание
- 1. Теория игр
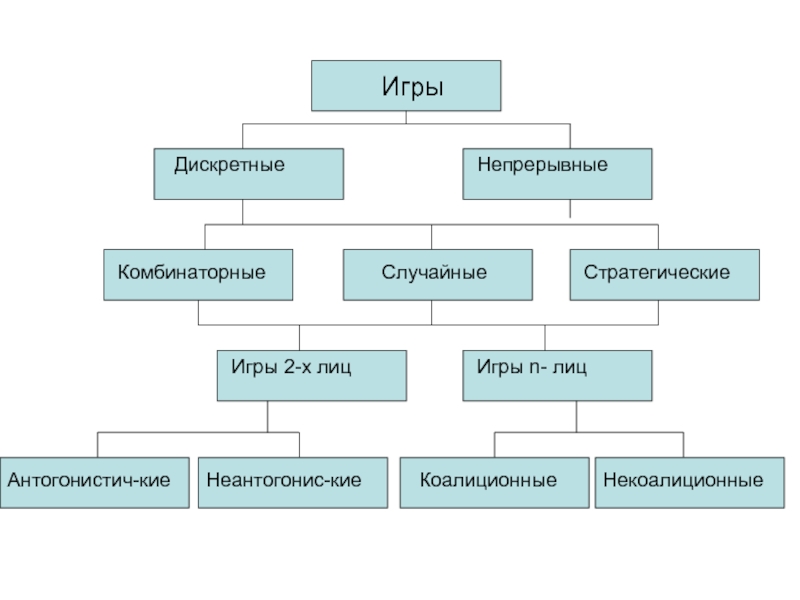
- 2. ИгрыДискретныеНепрерывныеКомбинаторныеСлучайныеСтратегическиеИгры 2-х лицИгры n- лицАнтогонистич-киеНеантогонис-киеКоалиционныеНекоалиционные
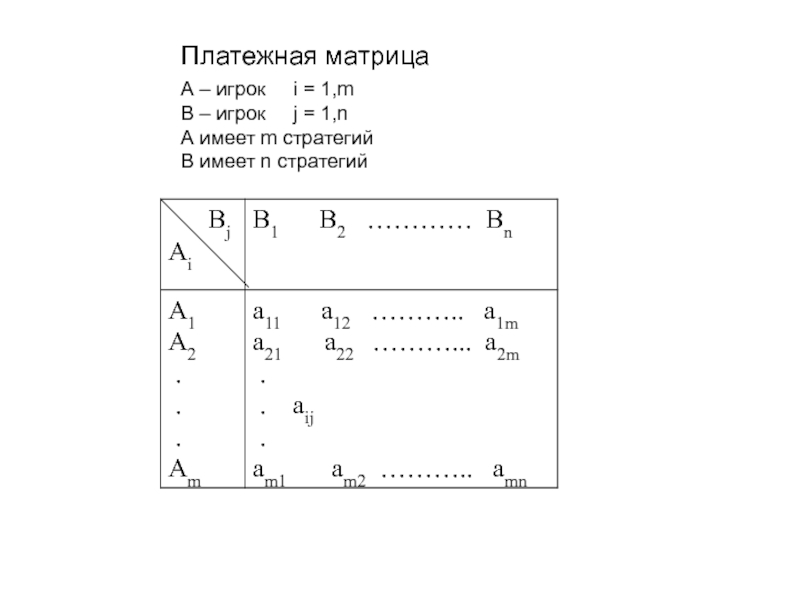
- 3. Платежная матрица А – игрок
- 4. Принцип минимакса
- 5. Принцип минимаксаИз каждой строчки выбирается минимальное значение:
- 6. Пример 3. Игра «Вооружение и самолеты»Здесь
- 7. Игры со смешанной стратегиейα = β =
- 8. Смешанная стратегияИгрок А имеет m стратегийp1, p2,
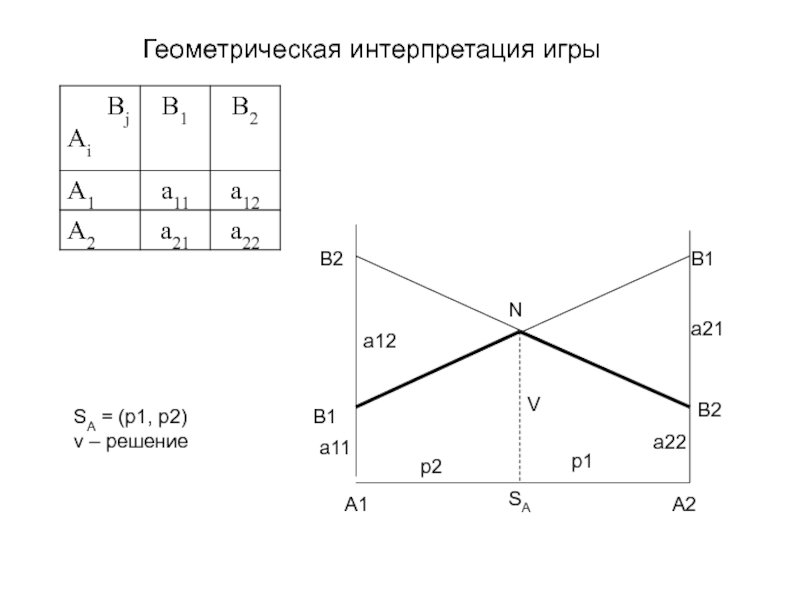
- 9. Геометрическая интерпретация игры A1A2B1B1B2B2a11a21a22a12p1p2SANSA = (p1, p2)ν – решениеV
- 10. p | 6 4 3 1 -1 01-p| -2 -1 1 0 5 4Чистые стратегии для игрока BW1
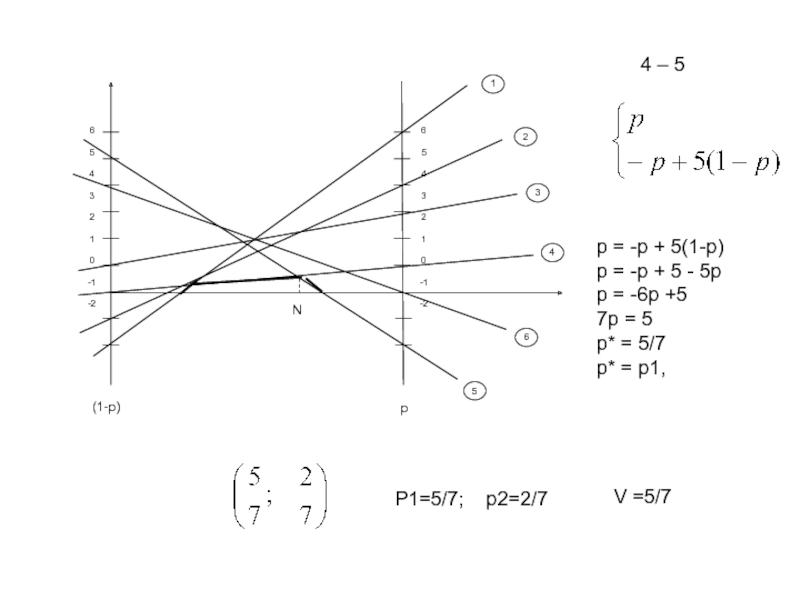
- 11. p = -p + 5(1-p)p = -p
- 12. Смешанные стратегииПример. Имеются 4 образца зенитных управляемых
- 13. Требуется, исходя из принципов теории игр, обосновать
- 14. Решение. Замечаем, что стратегия А1 заведомо невыгодна
- 15. Остается игра 2 х 3 с матрицей:
- 16. Игры против «природы»Пусть у нас m возможных
- 17. Пример. Планируется операция в заранее неясных условиях,
- 18. Критерий, основанный на вероятностных условияхПроще решать задачу
- 19. Критерии Вальда, Сэвиджа и ГурвицаПример. Рассматривается игра с природой 4 х 3. Найти оптимальное решение.
- 20. Критерий максиминный Вальда. F=max min aijВ каждой
- 21. Критерий минимаксного риска Сэвиджа F=min max rijОптимальной является любая из стратегий А2, А3
- 22. Критерий пессимизма-оптимизма Гурвица F=max(q min aij +
- 23. Дилемма заключенного
- 24. ПримерШвейное предприятие реализует свою продукцию через магазин.
- 25. РЕШЕНИЕ Составим математическую модель задачи. В связи
- 26. 2. Если фирма примет стратегию F1, а
- 27. Рассматривая фирму и природу в качестве двух
- 28. Слайд 28
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Теория игр
Математическая дисциплина, предметом исследования которой является методы принятия решений
в конфликтных ситуациях.
или более лиц преследующих противоположные цели.Слайд 2Игры
Дискретные
Непрерывные
Комбинаторные
Случайные
Стратегические
Игры 2-х лиц
Игры n- лиц
Антогонистич-кие
Неантогонис-кие
Коалиционные
Некоалиционные
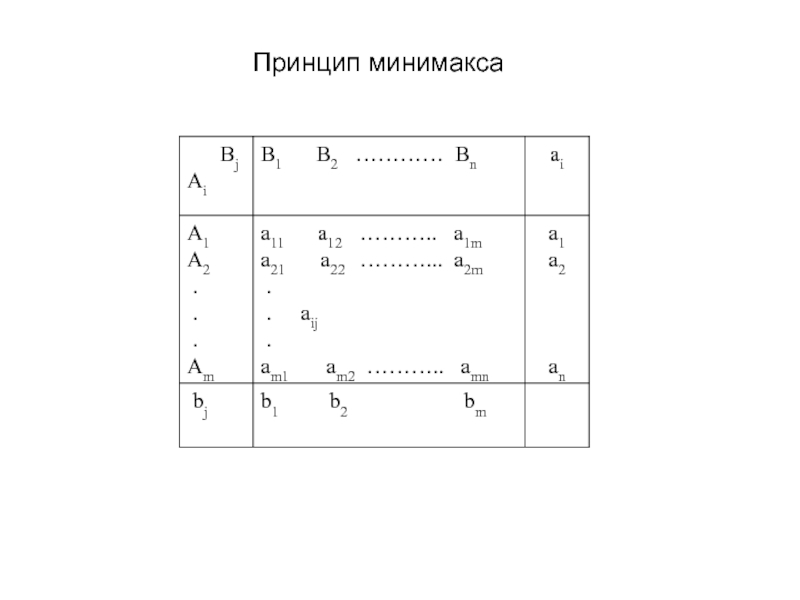
Слайд 5Принцип минимакса
Из каждой строчки выбирается минимальное значение: ai = min
aij
α = max ai; α = max
ai из min aij.α – нижняя цена игры. Игрок должен придерживаться стратегии max- min (максимином)
α гарантирует минимум, который можно получить придерживаясь максиминной стратегии.
bj = max aij ; βj = min bj ; βj = min max aij
β – верхняя цена игры Это минимаксная стратегия.
Когда α = β, то система устойчива.
Слайд 6
Пример 3. Игра «Вооружение и самолеты»
Здесь α=β, то есть система
устойчива
0.7 –это чистая цена игры
Слайд 7Игры со смешанной стратегией
α = β = ν – чистая
цена игры;
игры с седловой точкой; игры с полной информацией
(противники знают все ходы). Такие игры являются устойчивыми.
.
α ≠ β
α ≤ γ ≤β
α – нижняя цена игры
β – верхняя цена игры
Случайная величина, значением которой является стратегия игрока, называется смешанной стратегией.
Слайд 8Смешанная стратегия
Игрок А имеет m стратегий
p1, p2, ……, pm
∑ pi
=1
Игрок B – n стратегий
q1, q2, ……, qn
∑ qj =1
P = (p1, p2, ……, pm)Q = (q1, q2, ……., qn)
H(P,Q) = ∑ ∑ aij pi qj – математич.ожид-ие выигрыша игрока А в смеш.стратегии
Слайд 10p | 6 4 3 1 -1 0
1-p| -2 -1 1 0 5 4
Чистые стратегии для игрока B
W1 = 6p –
2(1-p)
W2 = 4p – (1-p)
W3 = 3p – (1-p)
W4 =
pW5 = -p – 5(1-p)
W6 = 4(1-p)
Игра 2 х 6
Слайд 12Смешанные стратегии
Пример.
Имеются 4 образца зенитных управляемых ракет: А1, А2,
А3, А4, предназначенных для стрельбы по самолетам. Известны типы самолетов
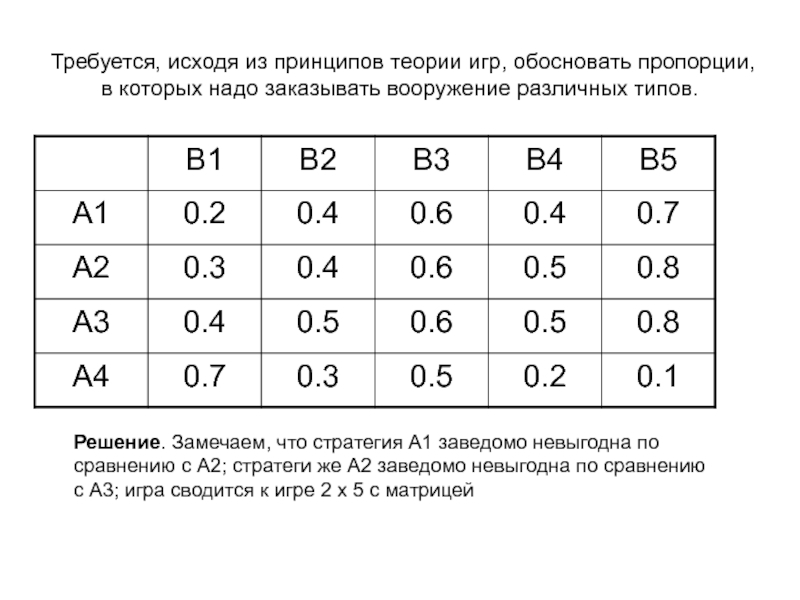
противника В1,В2,В3,В4,В5. Вероятность поражения самолета противника при применении каждого типа вооружения задана матрицей.Слайд 13Требуется, исходя из принципов теории игр, обосновать пропорции, в которых
надо заказывать вооружение различных типов.
Решение. Замечаем, что стратегия А1 заведомо
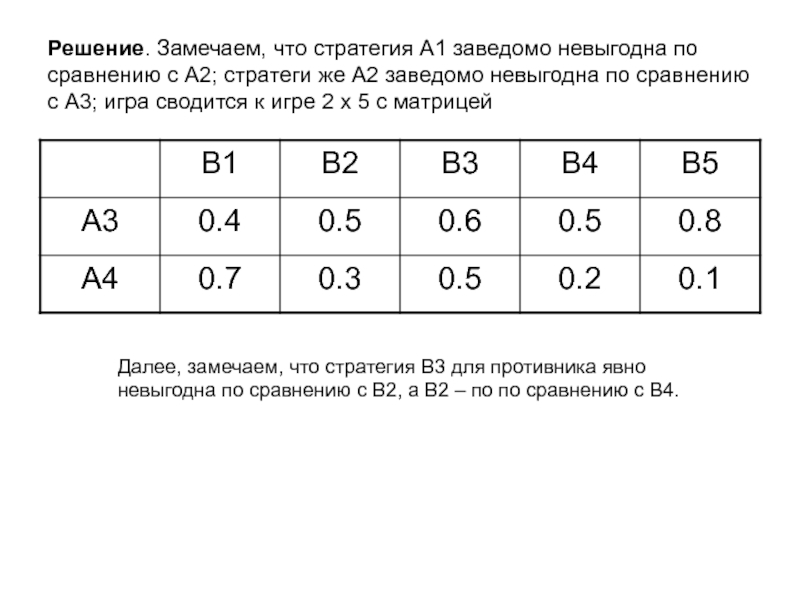
невыгодна по сравнению с А2; стратеги же А2 заведомо невыгодна по сравнению с А3; игра сводится к игре 2 х 5 с матрицейСлайд 14Решение. Замечаем, что стратегия А1 заведомо невыгодна по сравнению с
А2; стратеги же А2 заведомо невыгодна по сравнению с А3;
игра сводится к игре 2 х 5 с матрицейДалее, замечаем, что стратегия В3 для противника явно невыгодна по сравнению с В2, а В2 – по по сравнению с В4.
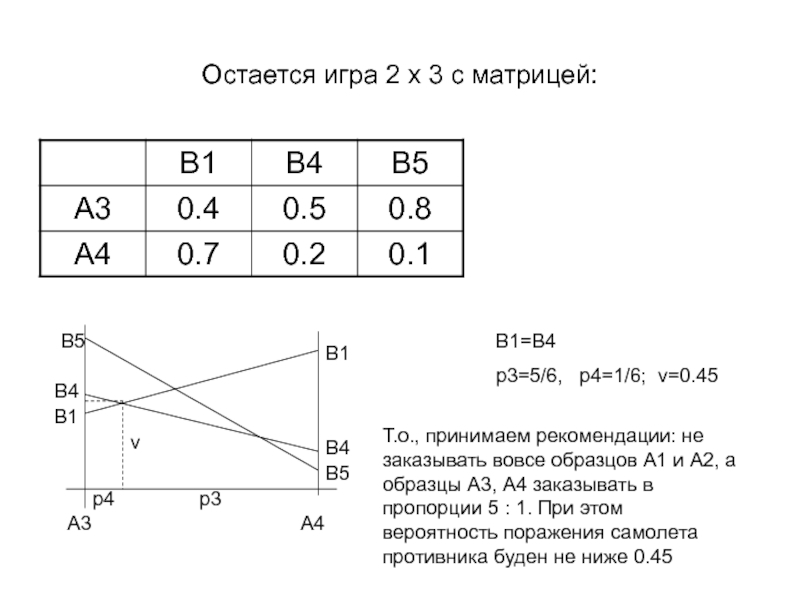
Слайд 15Остается игра 2 х 3 с матрицей:
В1
В1
В4
В4
В5
В5
p3
p4
В1=В4
p3=5/6, p4=1/6;
v=0.45
Т.о., принимаем рекомендации: не заказывать вовсе образцов А1 и
А2, а образцы А3, А4 заказывать в пропорции 5 : 1. При этом вероятность поражения самолета противника буден не ниже 0.45v
А3
А4
Слайд 16Игры против «природы»
Пусть у нас m возможных стратегий: А1, А2,
… ,Аm, а П1, П2, … ,Пn – «стратегии природы».
Может показаться, что при наличии природы задача проще, так как нет противодействия. Но при наличии сознательного противника у нас как бы снимается неопределенность.В данной ситуации (при играх с природой) неопределенность сказывается в гораздо более сильной степени.
В игре против разумного противника мы можем отбросить за него какие то невыгодные для него стратегии Вj.
В игре против природы этого делать нельзя.
В игре против природы рекомендуется использовать понятие «риска».
Риском наз.разность между выигрышем, который получил бы А, если бы знал Пj, и выигрышем, который он получит в тех же условиях, применяя стратегию Аi.
Риск: rij =bj – aij , где bj = max aij,,
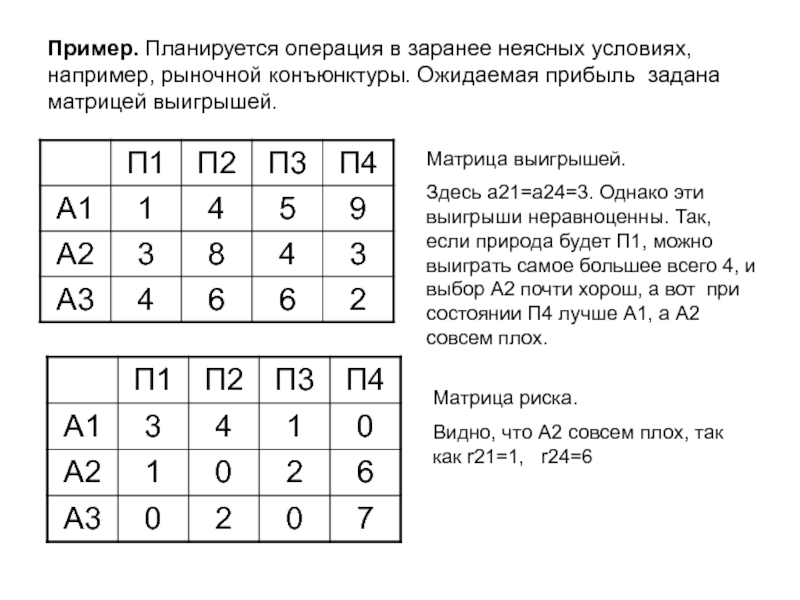
Слайд 17Пример. Планируется операция в заранее неясных условиях, например, рыночной конъюнктуры.
Ожидаемая прибыль задана матрицей выигрышей.
Матрица выигрышей.
Здесь а21=а24=3. Однако эти выигрыши
неравноценны. Так, если природа будет П1, можно выиграть самое большее всего 4, и выбор А2 почти хорош, а вот при состоянии П4 лучше А1, а А2 совсем плох.Матрица риска.
Видно, что А2 совсем плох, так как r21=1, r24=6
Слайд 18Критерий, основанный на вероятностных условиях
Проще решать задачу в условиях неопределенности,
когда известны вероятности состояний природы: qi=P(Пi).
В этом случае
среднее значение: ai*=q1 х ai1+q2 х ai2+ … + qn х ainПример. Планируется операция в заранее неизвестных метеорологических условиях. Известны вероятности.
Видно. Оптимальной стратегией игрока является его стратегия А*=А1, дающая среднтй выигрыш 5.2
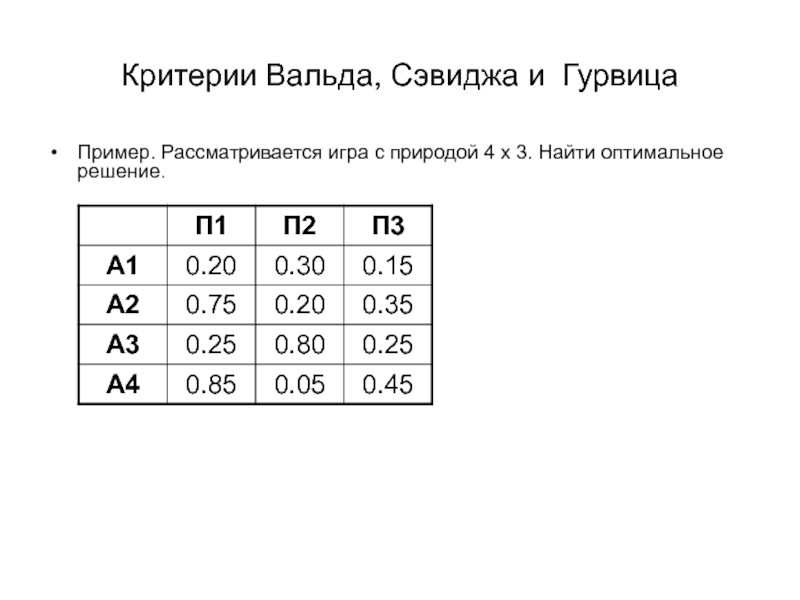
Слайд 19Критерии Вальда, Сэвиджа и Гурвица
Пример. Рассматривается игра с природой 4
х 3. Найти оптимальное решение.
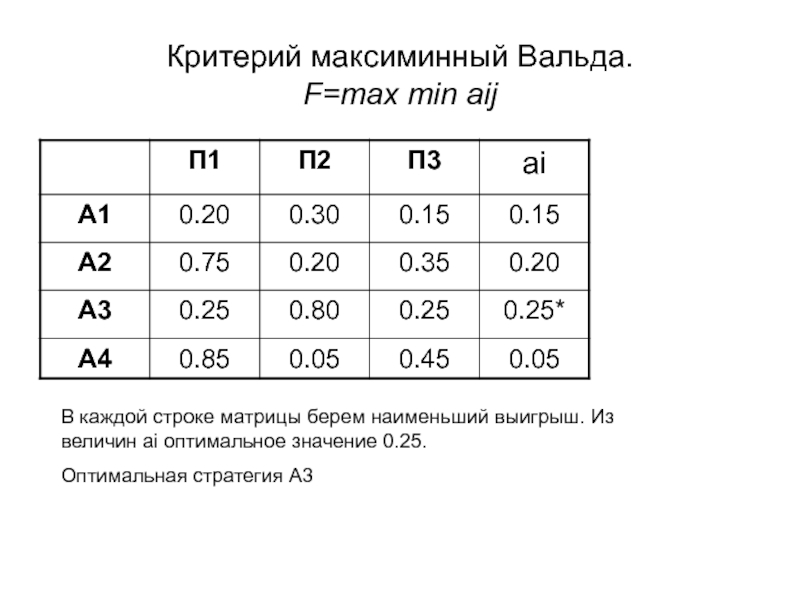
Слайд 20Критерий максиминный Вальда.
F=max min aij
В каждой строке матрицы берем наименьший
выигрыш. Из величин ai оптимальное значение 0.25.
Оптимальная стратегия А3
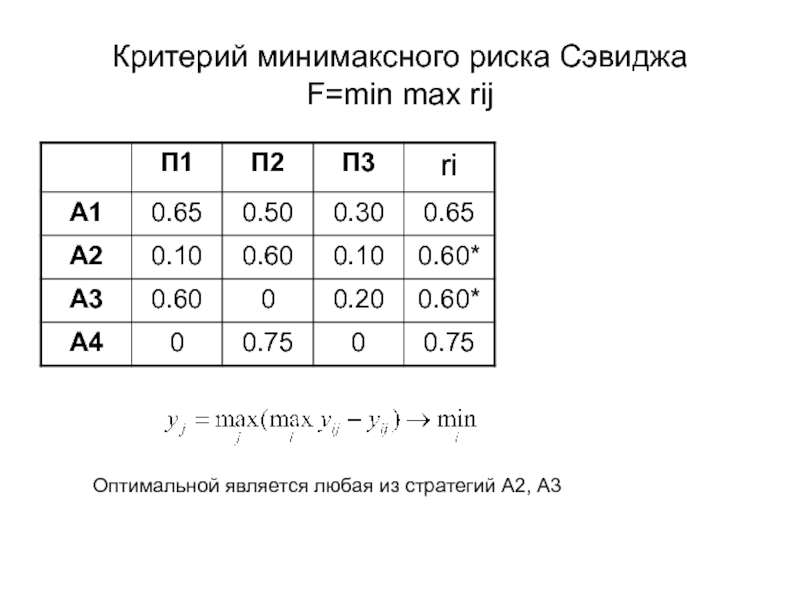
Слайд 21Критерий минимаксного риска Сэвиджа
F=min max rij
Оптимальной является любая из стратегий
А2, А3
Слайд 22Критерий пессимизма-оптимизма Гурвица
F=max(q min aij + (1-q) max aij) q=0.6
Записываем
в правых трех столбцах матрицы пессимистическую оценку выигрыша ai, оптимистическую
wi и их среднее взвешенное по формуле hi=0.6ai + 0.4wiЗдесь 0.6 легкий перевес в сторону пессимизма.
Оптимальная стратегия А3
Слайд 24Пример
Швейное предприятие реализует свою продукцию через магазин. Сбыт зависит от
состояния погоды.
В условиях теплой погоды предприятие реализует
1000 костюмов
и 2300 платьев,а при прохладной погоде - 1400 костюмов и 700 платьев.
Затраты на изготовление одного костюма равны 20, а платья - 5 рублям, цена реализации соответственно равна 40 рублей и 12 рублей.
Определить оптимальную стратегию предприятия.
Слайд 25РЕШЕНИЕ
Составим математическую модель задачи.
В связи с возможными состояниями
спроса фирма располагает двумя стратегиями:
1. F1 = (1000, 2300)
– произвести 1000 костюмов и 2300 платьев, 2. F2 = (1400, 700) - произвести 1400 костюмов и 700 платьев. Природа (рынок) располагает также двумя стратегиями:
1. D1 = погода теплая,
2. D2 = погода прохладная.
Слайд 262. Если фирма примет стратегию F1, а спрос будет находиться
в состоянии D2 (погода прохладная), то платья будут реализованы лишь
частично, и доход составит:w12 = 1000*(40-20) + 700*(12-5) – (2300-700)*5= 16900.
3.Аналогично, если фирма выберет стратегию F2,
а природа – стратегию D1 (погода теплая), то доход составит (будут недораспроданы костюмы):
w21 =1000*(40-20) + 700*(12-5) – (1400-1000)*20= 16900,
4. Если природа выберет стратегию D2, то
w22 = 1400*(40-20) + 700*(12-5) = 32900.
1. Если фирма примет стратегию F1 и спрос действительно будет находиться в первом состоянии, то есть погода будет теплой (D1), то выпущенная продукция будет полностью реализована и доход составит w11 =1000*(40-20) + 2300*(12-5) = 36100
Слайд 27Рассматривая фирму и природу в качестве двух игроков, получим платежную
матрицу игры
36100 16900
16900 32900которая будет служить игровой моделью задачи.
Поскольку максиминная стратегия игры составляет
a = max (16900, 16900) = 16900,
а минимаксная
b = min (36100, 3290) = 32900,
то цена игры лежит в диапазоне 16900 ден. ед. < v < 32900 ден.ед.