Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория множеств
Содержание
- 1. Теория множеств
- 2. Георг Кантор(03.03.1845 - 06.01.1918) немецкий математик.
- 3. Бертран Расселл18 мая 1872 — 2 февраля 1970 — английский математик, философ и общественный деятель
- 4. Феликс Эдуард Жустин Эмиль Борель(7 января 1871 — 3 февраля 1956) — французский математик и политический деятель.
- 5. Понятие множестваПод «множеством» мы понимаем соединение в
- 6. Введение в теорию множеств 1. Основные определения,
- 7. Определение 1Множество А называется подмножеством В, если
- 8. Определение 3Множества А и В называются равными,
- 9. Определение 5
- 10. 2. Операции над множествамиОпределение 1Объединением двух множеств
- 11. Объединение множествТеорема 2Пусть А, В, С – произвольные
- 12. Пересечение множествОпределение 4Пересечением множеств А и В
- 13. Теорема 5Пусть А, В, С – произвольные множества,
- 14. Объединение и пересечение множествТеорема 61)2)3)4)
- 15. Разность множеств, дополнение, симметрическая разностьОпределение 1Разностью
- 16. Разность множествТеорема 2Пусть А, В, С – произвольные
- 17. Слайд 17
- 18. Дополнение множествОпределение 4Пусть U – универсальное множество. Дополнением
- 19. Дополнение множествТеорема 51)2)3)Теорема 6(законы Моргана для дополнений)а)
- 20. Симметрическая разностьОпределение 7Симметрической разностью множеств A и B называют множествоЗадача (3 балла).Доказать, что AB
- 21. Парадокс РасселлаПусть K — множество всех множеств, которые
- 22. Другие формулировки парадокса РасселлаПарадокс Брадобрея:Одному деревенскому брадобрею
- 23. Решение задач
- 24. 1. Вычисление множеств
- 25. 2. Выражение множествПусть U={1, 2, 3, 4,
- 26. 3. Изображение множеств с помощью кругов Эйлера
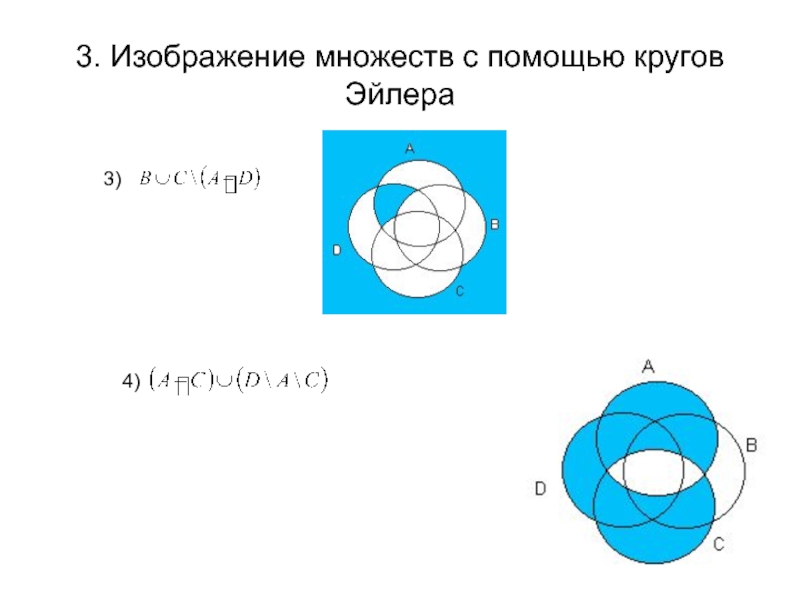
- 27. 3. Изображение множеств с помощью кругов Эйлера3) 4)
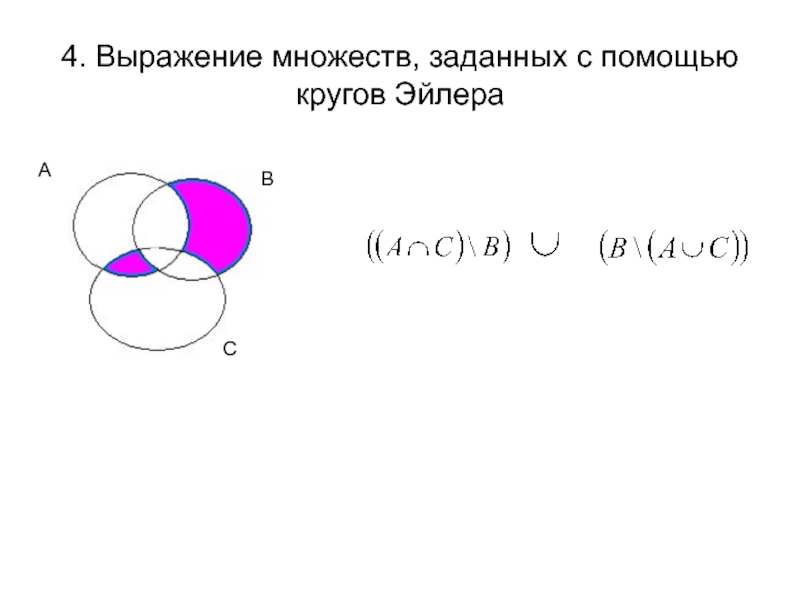
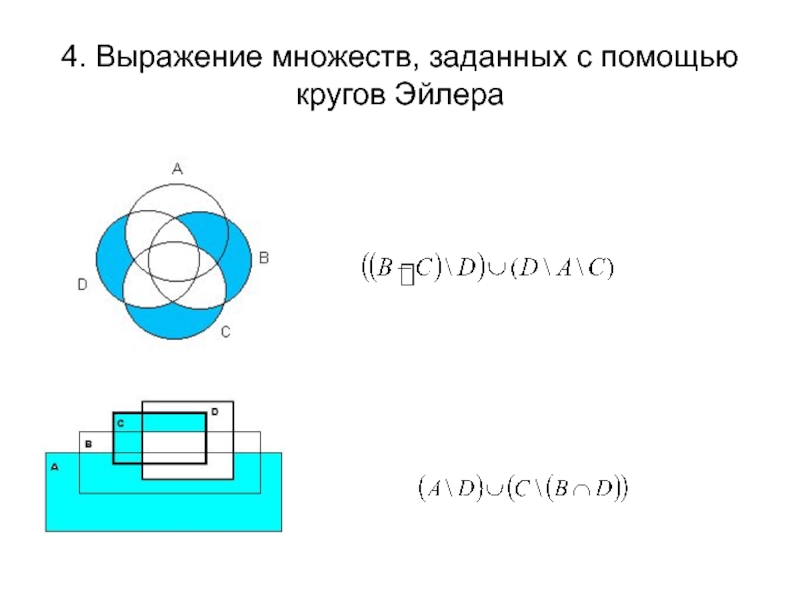
- 28. 4. Выражение множеств, заданных с помощью кругов Эйлера
- 29. 4. Выражение множеств, заданных с помощью кругов Эйлера
- 30. Декартово произведение
- 31. Декартово произведение Под упорядоченной парой (а; b)
- 32. Декартово произведениеОпределение 2а) Множество называется декартовым произведением
- 33. Декартово произведениеЗадачаИзобразить множество ПримерОчевидно, что
- 34. Декартово произведениеТеорема 3Пусть А, В, С – произвольные множества, тогда
- 35. Декартово произведениеТеорема 4Если множество А состоит из
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Феликс Эдуард Жустин Эмиль Борель
(7 января 1871 — 3 февраля 1956) —
французский математик и политический деятель.
Слайд 5Понятие множества
Под «множеством» мы понимаем соединение в некое целое M
определённых хорошо различимых предметов m нашего созерцания или нашего мышления
(которые будут называться «элементами» множества M).(Г. Кантор).
Множество есть совокупность различных элементов, мыслимая как единое целое.
(Б. Расселл)
Каждый сам знает, что он понимает под множеством.
(Э. Борель)
Слайд 6Введение в теорию множеств
1. Основные определения, терминология
Под множеством А
мы понимаем совокупность объектов произвольной природы, объединенных общим свойством Р(х).
Обозначение
Указанием
определяющего свойстваПеречислением элементов
Пример 1
Иногда второе обозначение распространяется и на некоторые бесконечные множества. Так,
N={1,2,3,...,n,...}
Z={...,-n,...,-2,-1,0,1,2,...,n,...}.
Слайд 7Определение 1
Множество А называется подмножеством В, если для любого х
(
)Обозначение:
Другими словами, символ " " есть сокращение для высказывания Теорема 2
Для любых множеств А, В, С верно следующее:
а) ;
б) и .
Слайд 8Определение 3
Множества А и В называются равными, если они состоят
из одних и тех же элементов (A=В). Другими словами, обозначение
А=В служит сокращением для высказывания.
Пример
Указать равные множества
A={0;1;2}, B = {1;0;2}, C={0;1;2;0}, D={{1;2};0},
E={1;2}, F={x:x3-3x2+2x=0}.
Теорема 4
Для любых множеств А и В А=В тогда и только тогда, когда
и
Доказательство
Доказательство этого факта основано на том, что эквивалентность равносильна конъюнкции двух импликаций
Слайд 9
Определение 5
тогда
и только тогда, когда
и .Теорема 6
Для любых множеств А, В, С, если и , то
Определение 7
Множество называется пустым, если оно не содержит ни одного элемента, то есть х не принадлежит этому множеству (для любого х).
Обозначение: .
Слайд 102. Операции над множествами
Определение 1
Объединением двух множеств А и В
называется множество
Пример
Пусть А={1,2,3,4}, B={2,4,6,8}, тогда
= {1,2,3,4,6,8}.A
B
Слайд 11Объединение множеств
Теорема 2
Пусть А, В, С – произвольные множества. Тогда:
а)
– идемпотентность объединения;
б) – коммутативность объединения;
в) – ассоциативность объединения;
г) ;
д)
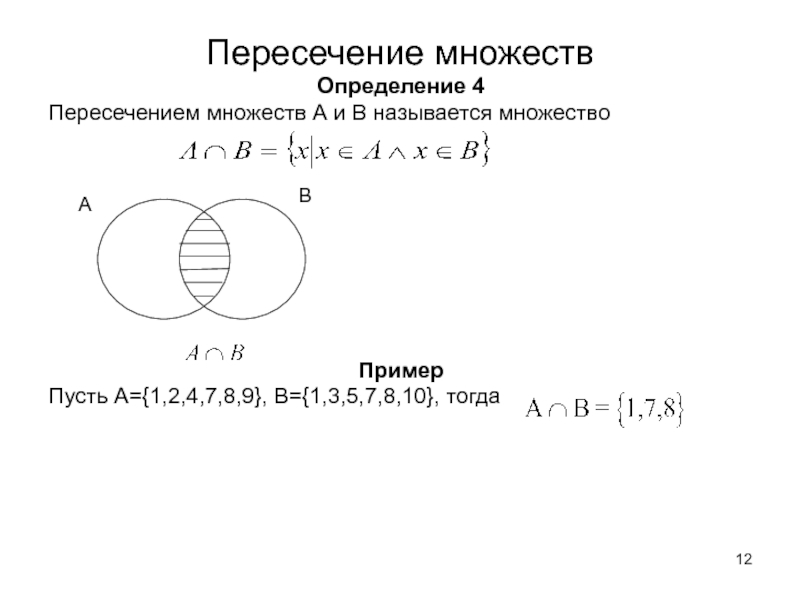
Слайд 12Пересечение множеств
Определение 4
Пересечением множеств А и В называется множество
Пример
Пусть A={1,2,4,7,8,9}, B={1,3,5,7,8,10}, тогда
A
B
Слайд 13Теорема 5
Пусть А, В, С – произвольные множества, тогда:
а)
- идемпотентность
пересечения;б) - коммутативность пересечения;
в) - ассоциативность пересечения;
г)
Пересечение множеств
Слайд 15 Разность множеств, дополнение, симметрическая разность
Определение 1
Разностью множеств A и
B называется множество
.Пример
Пусть А={1,3,4,7,8,9,10}, B={2,3,4,5,6,7}, тогда A\B={1,8,9,10}, B\A={2,5,6}.
A
B
Слайд 16Разность множеств
Теорема 2
Пусть А, В, С – произвольные множества, тогда:
1)
2)
3)
4)
Теорема 3
(законы Моргана)
а)
б)
Слайд 17
Множество U назовем "универсальным", если оно содержит все элементы и все множества являются его подмножествами. Понятие "универсального множества" у нас будет зависеть от круга задач, которые мы рассматриваем. Довольно часто под универсальным множеством понимают множество R –– множество вещественных чисел или множество С – комплексных чисел. Возможны и другие примеры. Всегда в контексте необходимо оговорить, что мы понимаем под универсальным множеством U.
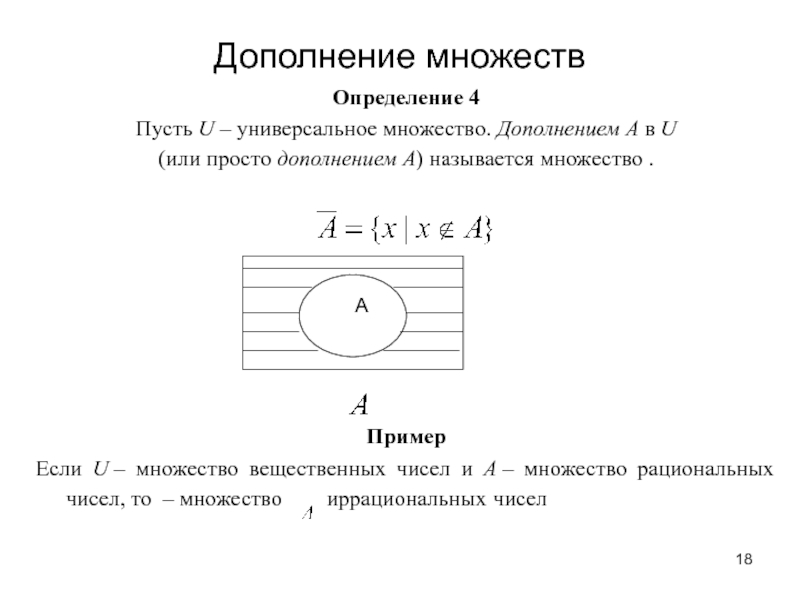
Слайд 18Дополнение множеств
Определение 4
Пусть U – универсальное множество. Дополнением А в U
(или просто дополнением А) называется множество .
Пример
Если U – множество вещественных
чисел и А – множество рациональных чисел, то – множество иррациональных чисел A
Слайд 20Симметрическая разность
Определение 7
Симметрической разностью множеств A и B называют множество
Задача
(3 балла).
Доказать, что
A
B
Слайд 21Парадокс Расселла
Пусть K — множество всех множеств, которые не содержат себя
в качестве своего элемента. Содержит ли K само себя в
качестве элемента?Слайд 22Другие формулировки парадокса Расселла
Парадокс Брадобрея:
Одному деревенскому брадобрею приказали «брить всякого,
кто сам не бреется, и не брить того, кто сам
бреется», как он должен поступить с собой?Парадокс Мэра:
В одной стране вышел указ: «Мэры всех городов должны жить не в своем городе, а в специальном Городе мэров», где должен жить мэр Города мэров?
Парадокс библиотеки:
Некая библиотека решила составить библиографический каталог, в который входили бы все те и только те библиографические каталоги, которые не содержат ссылок на самих себя. Должен ли такой каталог включать ссылку на себя?
Слайд 241. Вычисление множеств
Дано
U={1;2;3;4;5;6;7;8;9;10;11},
A={1;2;3;7;9},
B={3;4;5;6;10;11},
C={2;3;4;7;8},
D={1;7;11}.
Вычислить
множества1)
2)
3)
4)
5)
Слайд 25
2. Выражение множеств
Пусть U={1, 2, 3, 4, 5, 6, 7,
8,9},
A={1, 2, 3, 5},
B={2, 4, 6, 8},
C={1, 3, 5, 7},
D={4,
5, 7, 8}.Выразить через известные множества A, B, C, D следующие множества.
{1,2,3,4,5,7,8}=
{4,7,8}=
{2,5,6,7}=
{2,5}=
{5,7,9}=
{4,5}=
Невозможно выразить через данные множества, так как элементы 4 и 8
одновременно принадлежат или не принадлежат данным множествам.
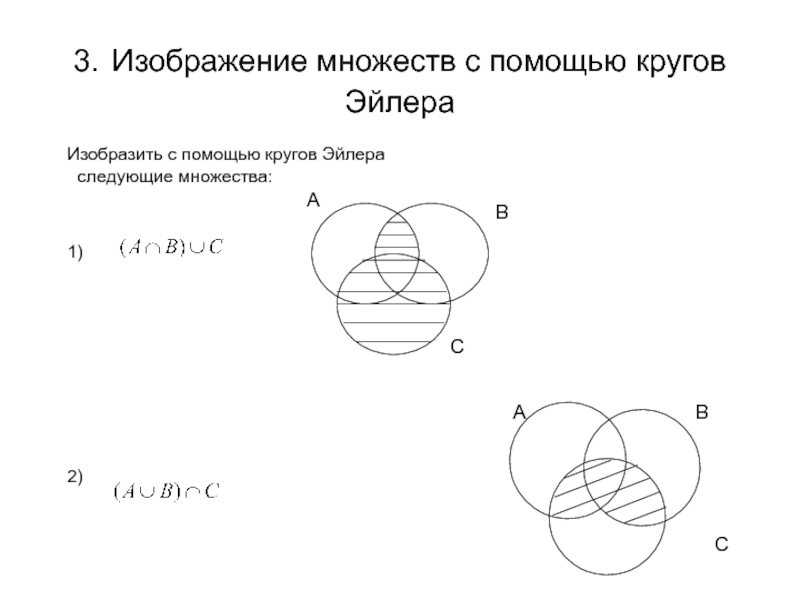
Слайд 263. Изображение множеств с помощью кругов Эйлера
Изобразить с
помощью кругов Эйлера следующие множества:
1)
2)
Слайд 31Декартово произведение
Под упорядоченной парой (а; b) мы будем понимать
двухэлементное множество,
состоящее из элементов а и b, в котором
зафиксирован порядок расположения элементов. Отметим два характерных свойства упорядоченных пар:
1) если
2)
Определение 1
Декартовым произведением множеств А и В называется множество
Пример
Пусть A={1;2}, B={a, b, c}, тогда
{(1;a);(1;b);(1;c);(2;a);(2;b);(2;c)};
{(a;1);(b;1);(c;1);(a;2);(b;2);(c;2)}.
Очевидно, что, вообще говоря,
Слайд 32Декартово произведение
Определение 2
а) Множество
называется декартовым произведением n множеств;
б)
- (n cомножителей) – n-aя декартова степень множества А;
Пример
Пусть , ,
Тогда
Слайд 33Декартово произведение
Задача
Изобразить множество
Пример
Очевидно, что
, где R-
множество действительных чисел,описывает множество всех точек декартовой плоскости
Решение
Слайд 35Декартово произведение
Теорема 4
Если множество А состоит из m элементов, а
В – из n элементов, тогда состоит из
mn элементов.Доказательство
ММИ по числу элементов множества B.
n=1.
то есть AB имеет m=m*1 элементов.
2) Допустим, что теорема верна при n=k.
3) И пусть теперь В состоит из к+1 элемента, то есть
где
Тогда , где
поэтому множество АВ состоит из mk+m=m(k+1) элементов.