Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ МНОЖЕСТВ C ООТВЕТСТВИЯ. ФУНКЦИИ. ОТОБРАЖЕНИЯ
Содержание
- 1. ТЕОРИЯ МНОЖЕСТВ C ООТВЕТСТВИЯ. ФУНКЦИИ. ОТОБРАЖЕНИЯ
- 2. Цель лекции – ознакомиться и овладеть понятием
- 3. Литература Горбатов В.А. Основы дискретной математики. М.:
- 4. ТерминыКлючевые слова: декартово (прямое) произведение множеств соответствие
- 5. Упорядоченная пара является одним из первичных понятий
- 6. Проекция вектора на осьДва вектора x, y
- 7. Координаты точки плоскости образуют упорядоченную пару: на
- 8. Декартово (прямое) произведение множеств 1Def: прямое (декартово) произведение
- 9. Декарту принадлежит координатное представление точек плоскостиМножество точек
- 10. Соответствия Def: соответствие – подмножество декартова произведения
- 11. Def: множество всех элементов yB, соответствующих элементу
- 12. Time Out
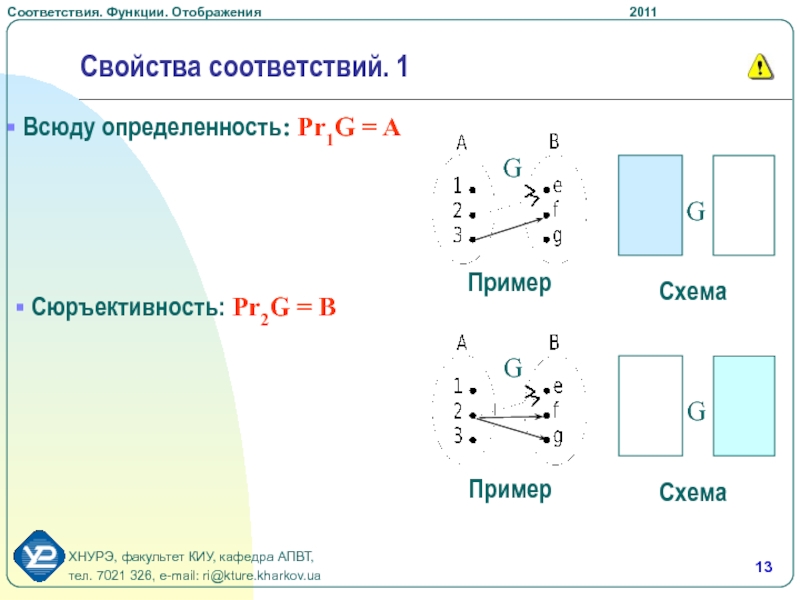
- 13. Свойства соответствий. 1 Всюду определенность: Pr1G = A Сюръективность: Pr2G = В
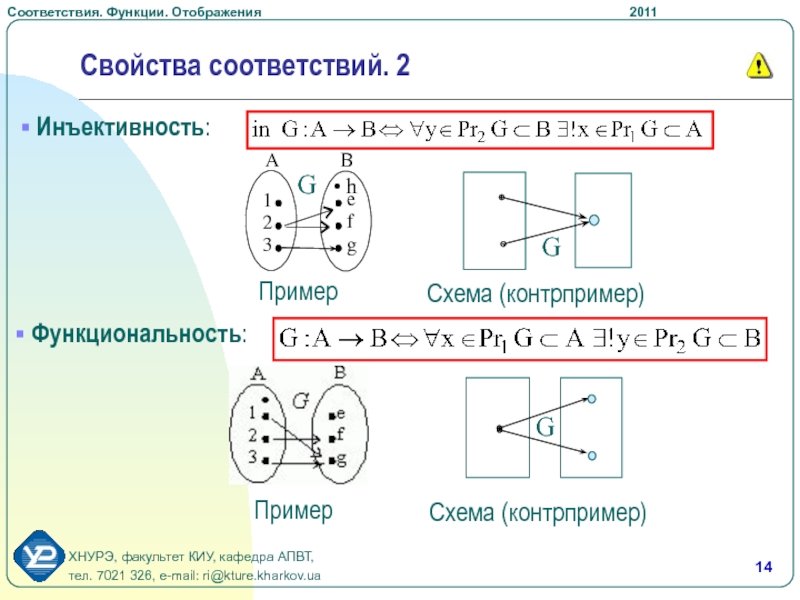
- 14. Свойства соответствий. 2 Функциональность:Пример Инъективность:
- 15. Соответствие взаимно-однозначно (биективно), если оно обладает одновременно
- 16. Соответствие G={ (x,y) | y = exp
- 17. Применение в задачах теории кодированияВиды кодирования: кодирование
- 18. Применение в задачах диагностированияПри диагностировании микросхем полупроводниковой
- 19. ВыводыСоответствие представляет собой произвольное подмножество декартова произведения
- 20. Тест-вопросы. 11. Могут ли повторяться компоненты вектора?а)
- 21. Тест-вопросы. 25. Отображение А в В это:а)
- 22. Тест-вопросы. 36. Верно ли: A,B AB=BA ?а)
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ТЕОРИЯ МНОЖЕСТВ
CООТВЕТСТВИЯ. ФУНКЦИИ. ОТОБРАЖЕНИЯ
Факультет компьютерной инженерии и управления, кафедра АПВТ,
ХНУРЭ
Слайд 2Цель лекции – ознакомиться и овладеть понятием «соответствие», изучить свойства
соответствий для применения в задачах компьютерной инженерии
Содержание:
Понятие упорядоченной
пары и вектораДекартово произведение множеств
Определение соответствия
Свойства соответствий
Взаимно-однозначное соответствие
Функции
Отображения
Примеры применения в теории кодирования и задачах диагностирования
Тема: Соответствия. Функции. Отображения
Слайд 3Литература
Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986.С.
9-12.
Тевяшев А.Д., Гусарова И.Г. Основы дискретной математики в примерах
и задачах. Харьков: ХТУРЭ, 2001. С. 11-17.Бондаренко М.Ф., Белоус Н.В., Руткас А.Г. Компьютерная дискретная математика. – Харьков: СМИТ, 2004. – 480 с.
Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Наука. Главная редакция физико-математической литературы, 1984. 4-10 с.
Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. М.: Энергия, 1980. 344 с.
Новиков Ф.А. Дискретная математика для программистов. С.-П., 2001. С. 4-24.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. 87с.
Хаханов В.И., Чумаченко С.В. Дискретная математика. Электронный учебник. ХНУРЭ: Электронная библиотека кафедры АПВТ (ауд. 320) NSERV\Library\Чумаченко\Дискретная математика\...
Слайд 4Термины
Ключевые слова:
декартово (прямое) произведение множеств
соответствие
всюду определенность
сюръективность
инъективность
функциональность
биекция (взаимная однозначность)
Базовые понятия:
множество
упорядоченная пара подмножество
Слайд 5Упорядоченная пара является одним из первичных понятий в теории множеств
Под
упорядоченной парой следует понимать двухэлементное упорядоченное множество
Вектор (кортеж) представляет собой
упорядоченный набор элементовх = (х1, х2, …, хn), где хi – координаты (компоненты)
Длина (размерность) вектора определяется количеством его координат
Основные понятия: упорядоченная пара, вектор
• Точка
Информация
Упорядоченная пара
Множество
Слайд 6Проекция вектора на ось
Два вектора x, y одинаковой размерности равны,
если их соответствующие компоненты равны:
x=y i xi=yi
Def: проекцией
вектора х=(х1, х2, …, хn) на i-ю ось называется его i-й компонент Pr i x = хiDef: пусть V – множество векторов одинаковой длины, тогда проекцией множества V на i-ю ось называется множество проекций всех векторов из V:
Слайд 7Координаты точки плоскости образуют упорядоченную пару: на первой позиции –
абсцисса, на второй – ордината. Они являются проекциями на первую
и вторую оси соответственноДано множество V векторов размерности 3:
V = { (a,b,c), (c,b,d), (b,b,d) }
Найти проекции множества V на оси
Примеры
Pr1V={a,c,b}
Pr2V={b}
Pr3V={c,d}
Слайд 8Декартово (прямое) произведение множеств 1
Def: прямое (декартово) произведение множеств A и
B есть множество всех упорядоченных пар (a,b) таких, что aA,
bB:AB={ (a,b) | aA, bB }
Примеры
1. Декартово произведение множеств А={1,2}, B={3,4,5} есть
АB = { (1,3), (1,4), (1,5), (2,3), (2,4), (2,5) }
2. A={1,2,3,4,5,6,7,8}, B={a,b,c,d,e,f,g,h}
АВ – обозначение клеток шахматной доски
Слайд 9Декарту принадлежит координатное представление точек плоскости
Множество точек плоскости RR=R2 есть
множество пар вида (a,b), aR, bR :
R2={(a,b) | aR, bR}
Декартов квадрат (А=В):
АА=А2={(a,b) | aА, bА}
Def: прямое произведение n множеств
А1А2 ¾ Аn ={(а1, а2, …… , аn)| aiАi , i=1,n}
Мощность декартова произведения множеств:
| А1А2 … Аn | = |А1 |•|А2|• ¾ •|Аn|
Рене Декарт
XVI-XVII вв.
Декартово (прямое) произведение множеств 2
Слайд 10Соответствия
Def: соответствие – подмножество декартова произведения двух множеств:
G
AB
А – область определения (множество отправления) соответствия G :
Pr1G={
x | (x,y)G }В – область значений (множество прибытия) соответствия G :
Pr2G={ y | (x,y)G }
Слайд 11Def: множество всех элементов yB, соответствующих элементу xA, называется образом
элемента х
в множестве B при соответствии G.
Def: множество
всех элементов xA, которым соответствует элемент yB, называется прообразом элемента y в множестве A при соответствии G.Пример
А={1,2,3}, B={e,f,g}
G={(1,e), (2,e)} AB
Образы и прообразы
G
образы
прообразы
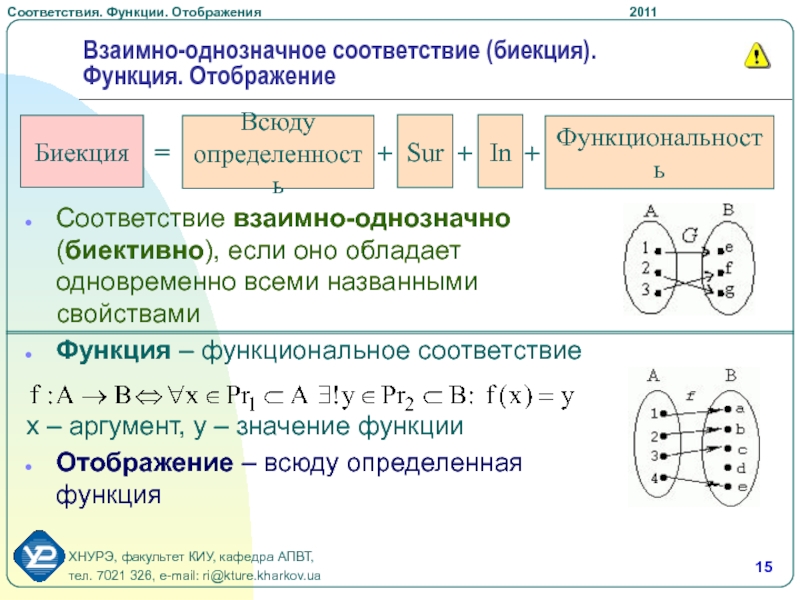
Слайд 15Соответствие взаимно-однозначно (биективно), если оно обладает одновременно всеми названными свойствами
Функция
– функциональное соответствие
x – аргумент, y – значение функции
Отображение –
всюду определенная функцияВзаимно-однозначное соответствие (биекция). Функция. Отображение
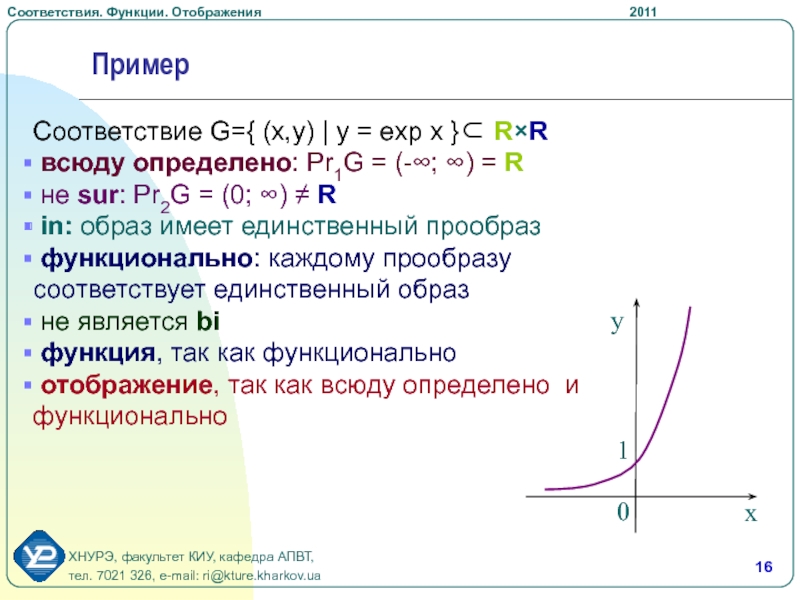
Слайд 16Соответствие G={ (x,y) | y = exp x } RR
всюду определено: Pr1G = (-; ) = R
не sur:
Pr2G = (0; ) Rin: образ имеет единственный прообраз
функционально: каждому прообразу соответствует единственный образ
не является bi
функция, так как функционально
отображение, так как всюду определено и функционально
Пример
Слайд 17Применение в задачах теории кодирования
Виды кодирования:
кодирование букв азбукой Морзе
представление чисел в системах счисления
секретные шифры
входящие и
исходящие номера в деловой переписке являются соответствиями между кодируемыми объектами и присваиваемыми им кодами
Они обладают всеми свойствами взаимно-однозначного соответствия, кроме сюръективности
Единственность образа и прообраза в кодировании гарантирует однозначность шифровки и дешифровки
Отсутствие сюръективности означает, что не каждый код имеет смысл. Например, кодирование телефонов шестизначными номерами не сюръективно
Слайд 18Применение в задачах диагностирования
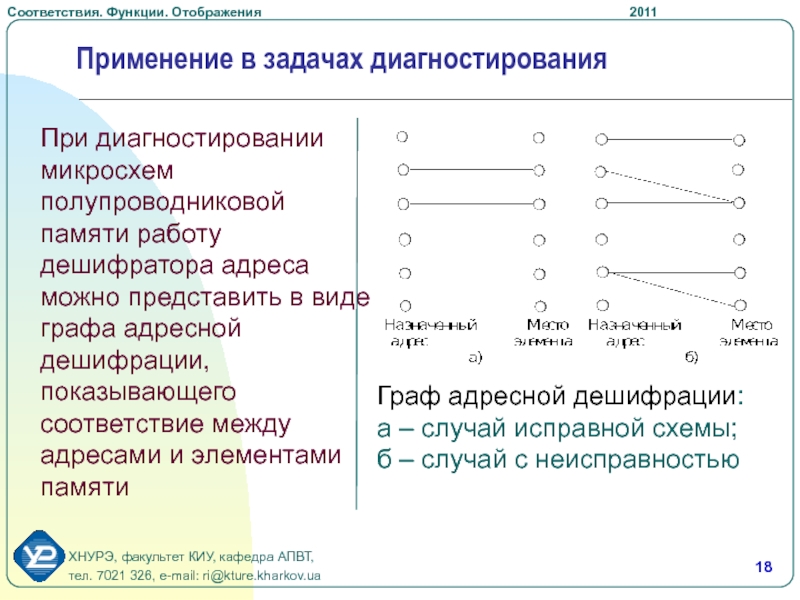
При диагностировании микросхем полупроводниковой памяти работу дешифратора
адреса можно представить в виде графа адресной дешифрации, показывающего соответствие
между адресами и элементами памятиГраф адресной дешифрации:
а – случай исправной схемы;
б – случай с неисправностью
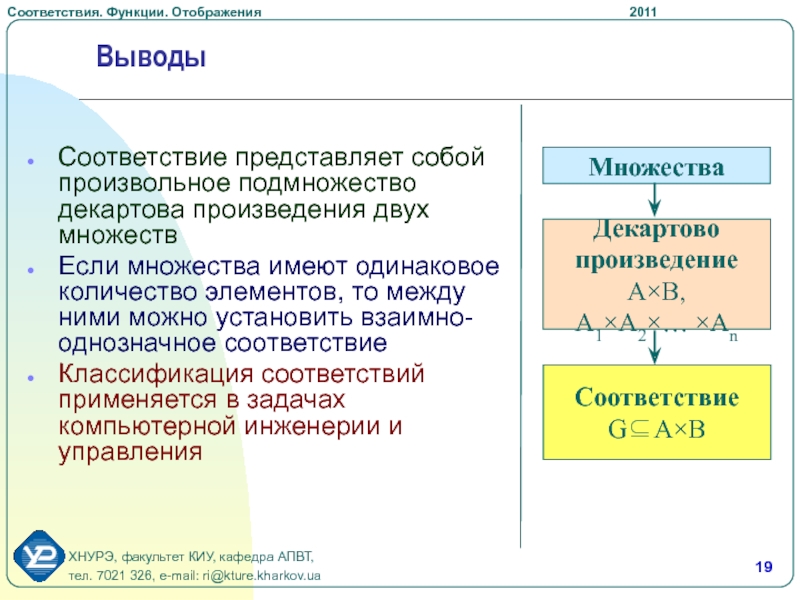
Слайд 19Выводы
Соответствие представляет собой произвольное подмножество декартова произведения двух множеств
Если множества
имеют одинаковое количество элементов, то между ними можно установить взаимно-однозначное
соответствиеКлассификация соответствий применяется в задачах компьютерной инженерии и управления
Слайд 20Тест-вопросы. 1
1. Могут ли повторяться компоненты вектора?
а) да; б) нет.
2.
Длина вектора
определяется:
а) числом различных
элементов;
б) числом координат.
3. Какое из
cоответствий
называется взаимно-
однозначным:
а) сюръективное,
инъективное и
функциональное?
б) сюръективное и
инъективное?
в) всюду определенное,
сюръективное,
инъективное и
функциональное?
Слайд 21Тест-вопросы. 2
5. Отображение А в В это:
а) частично определенная функция;
б) всюду определенная функция;
в) сюръективное соответствие;
г) инъективное соответствие.
4. Является
ли отображение биективным, если оно сюръективно и инъективно?а) да; б) нет.
Слайд 22Тест-вопросы. 3
6. Верно ли: A,B AB=BA ?
а) да;
б) нет.
7. Указать
проекцию множества A={(3,3,5), (3,3,6), (3,5,5), (3,5,6), (8,3,5), (8,3,6), (8,5,5), (8,5,6)}
на третью ось
а) PrA={3,8},
б) PrA={3,5},
в) PrA={5,6}.
8. Верно ли: |Аn| = |A|n ?
а) да
б) нет.
9. Соответствие является подмножеством
а) объединения двух множеств;
б) пересечения двух множеств;
в) теоретико-множественной разности двух множеств;
г) декартова произведения нескольких множеств;
д) декартова произведения двух множеств.