Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей и математическая статистика
Содержание
- 1. Теория вероятностей и математическая статистика
- 2. Лекция 1. Введение в теорию вероятностей Предметом
- 3. Равновозможные исходыРассмотрим некоторый опыт с конечным числом
- 4. Пусть n – число всех исходов, n(A)
- 5. Формулы комбинаторикиЧисло перестановок Число перестановок из n элементов равноСФУ Т.В. Крупкина
- 6. Выбор без возвращения Число размещений С помощью
- 7. Выбор без возвращенияЧисло сочетаний С помощью этой формулы
- 8. Статистическое определение вероятности Пусть рассматриваемый опыт можно
- 9. Статистическое определение вероятности Практика показывает, что для
- 10. Лекция 2. Основания теории вероятностейПространством элементарных исходов
- 11. Событиями мы будем называть некоторые наборы элементарных
- 12. Элементарные событияДостоверное событие Ω наступает при любом
- 13. Комбинации событийРассмотрим комбинации событий, такие, как сумма,
- 14. Суммой событий A1 и A2 называют событие
- 15. Противоположным событием к событию A называют событие
- 16. Вероятность в дискретном пространстве Чтобы определить вероятность
- 17. Несчетное множество исходовНо множество исходов не обязательно
- 18. Аксиоматическое определение вероятности Вероятность события есть числовая функция P(A), удовлетворяющая аксиомам: СФУ Т.В. Крупкина
- 19. Лекция 3. Исчисление вероятностейОпределение События A и B называются независимыми, если СФУ Т.В. Крупкина
- 20. Условная вероятность Условной вероятностью события A при условии,
- 21. Теорема сложенияСФУ Т.В. Крупкина
- 22. Теорема умножения для двух событий если соответствующие условные
- 23. Теорема (формула полной вероятности) Пусть A – случайное
- 24. Теорема (формула Байеса) Пусть A – случайное событие,
- 25. Лекция 4. Схемы испытаний Схемой испытаний Бернулли
- 26. Теорема (формула Бернулли)Обозначим через m число успехов в n испытаниях схемы Бернулли. ТогдаСФУ Т.В. Крупкина
- 27. Предельные теоремы для схемы Бернулли При числе испытаний,
- 28. Теорема Пуассона Если при n → ∞,
- 29. Приближенная формула Пуассона где λ = np.
- 30. Локальная приближенная формула Муавра –ЛапласаЛокальную приближенную формулу
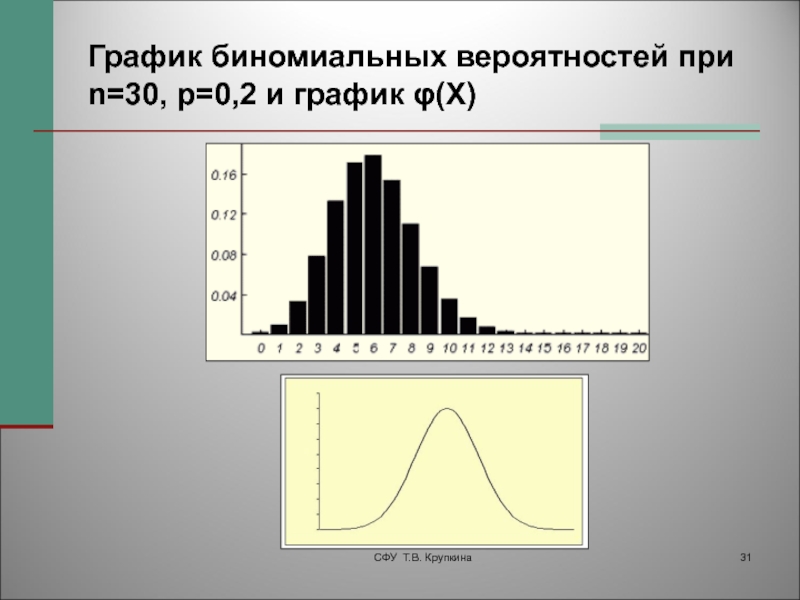
- 31. График биномиальных вероятностей при n=30, p=0,2 и график φ(X)СФУ Т.В. Крупкина
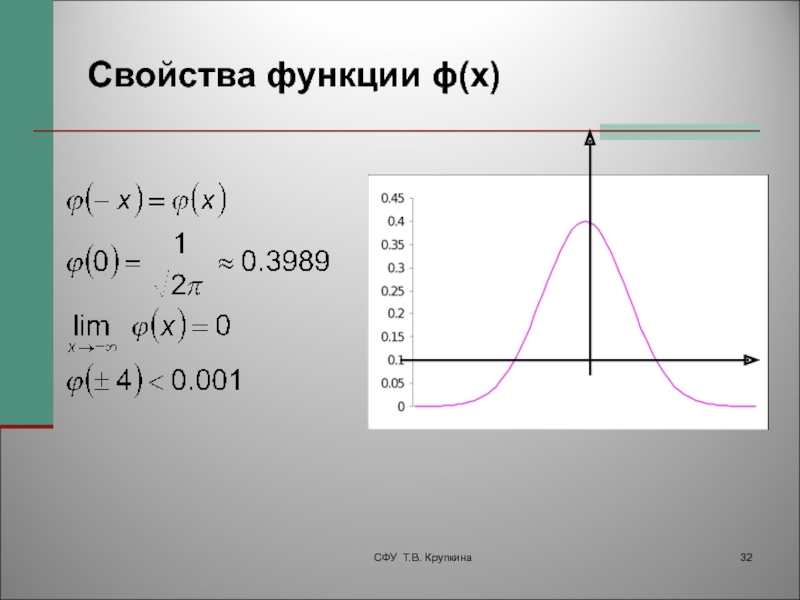
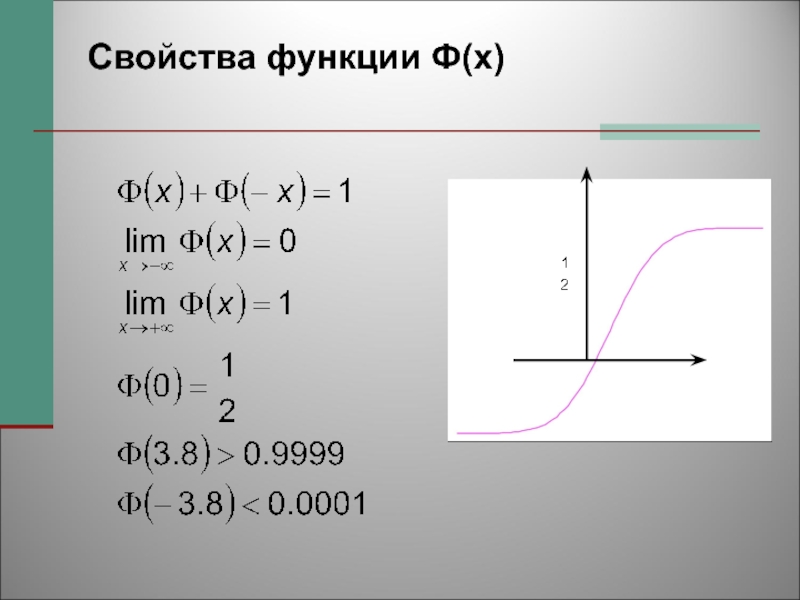
- 32. Свойства функции ϕ(x)СФУ Т.В. Крупкина
- 33. Интегральная приближенная формула Муавра –ЛапласаИнтегральную приближенную формулу
- 34. Свойства функции Ф(x)
- 35. Лекция 5. Дискретные случайные величины
- 36. Дискретные распределения Случайная величина ξ имеет дискретное распределение,
- 37. Ряд распределения Если случайная величина ξ
- 38. Биномиальное распределение B(n, p) Случайная величина ξ имеет
- 39. ПримерРаспределение вероятностей биномиально распределенной случайной величины для n = 10 и p = 0.2СФУ Т.В. Крупкина
- 40. Распределение Пуассона Pλ Сл. в. ξ имеет
- 41. Функция распределенияОпределение Функцией распределения случайной величины ξ называется
- 42. Лекция 6. Непрерывные распределения Случайная величина ξ
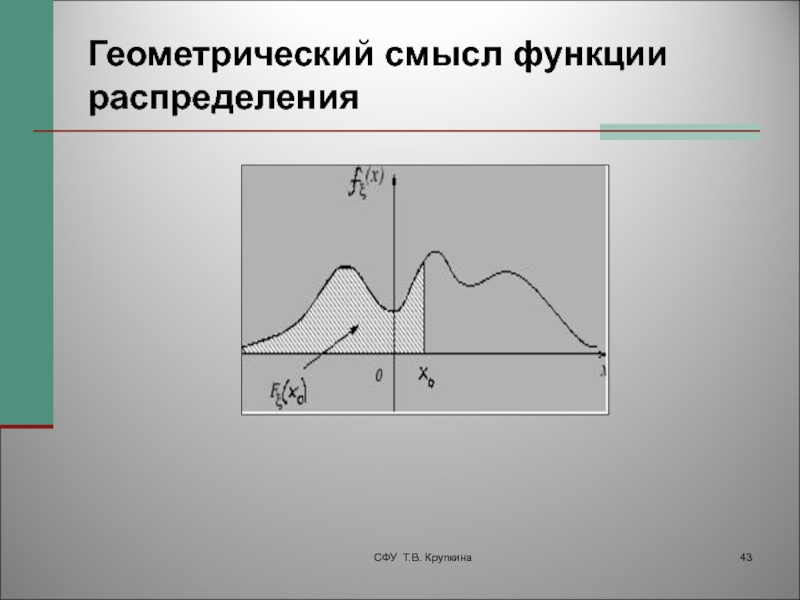
- 43. Геометрический смысл функции распределенияСФУ Т.В. Крупкина
- 44. Равномерное распределение R [a, b] СФУ Т.В. Крупкина
- 45. Нормальное распределение N (a,σ) СФУ Т.В. Крупкина
- 46. Нормальное распределение N (a,σ) Графики нормальных плотностей
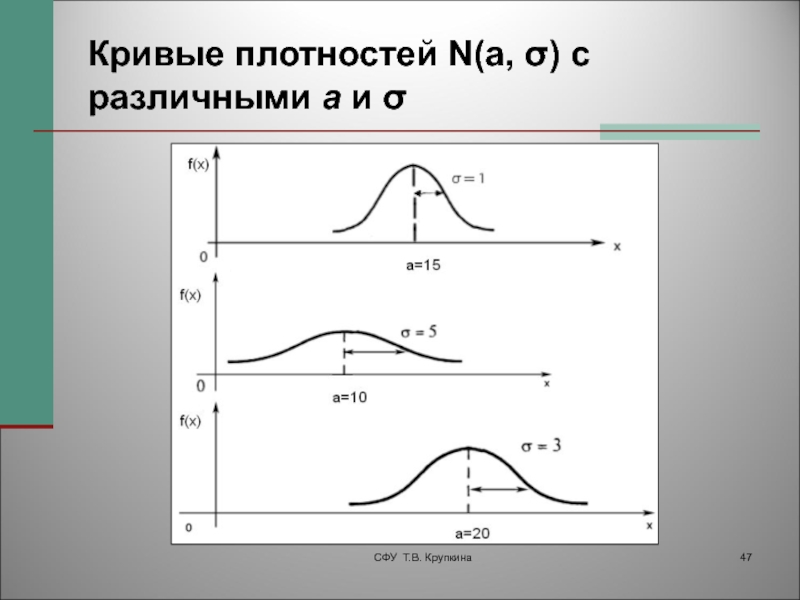
- 47. Кривые плотностей N(a, σ) с различными а и σСФУ Т.В. Крупкина
- 48. Плотность и функция распределения N(0,1)
- 49. Многомерные СВn – мерной случайной величиной ξ
- 50. Лекция 7. Числовые характеристики Математическим ожиданием Mξ
- 51. Математическим ожиданием Mξ непрерывно распределенной сл.
- 52. Математическое ожидание функции случайной величины
- 53. Дисперсия случайной величиныЕсли случайная величина ξ имеет
- 54. Числовые характеристики
- 55. Начальные и центральные моменты Начальным моментом k-го
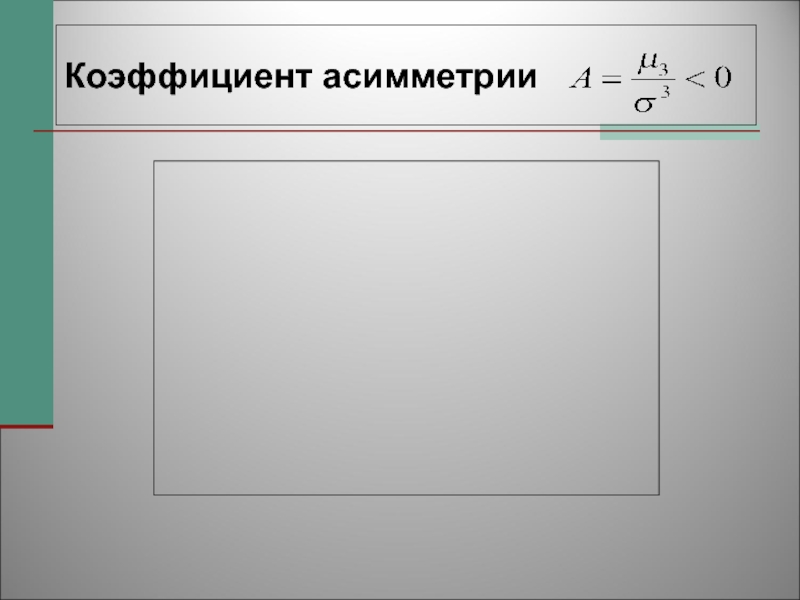
- 56. Коэффициент асимметрии
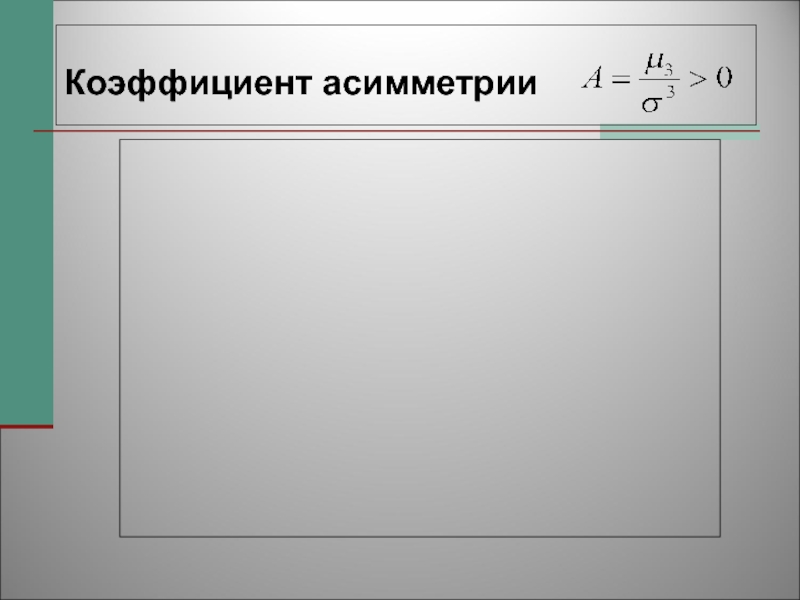
- 57. Коэффициент асимметрии
- 58. Коэффициент эксцесса
- 59. Лекция 8. Линейная зависимостьОпределение. Ковариацией случайной величины
- 60. Коэффициент корреляции Коэффициентом корреляции между случайными величинами ξ, η называется число
- 61. Свойства коэффициента корреляции1. │ρξη│≤ 1.2. Если ξ,η
- 62. Смысл коэффициента корреляции Коэффициент корреляции есть мера
- 63. Уравнение линейной регрессииУравнением линейной регрессии η на
- 64. Формулы уравнения линейной регрессииСФУ Т.В. Крупкина
- 65. Лекция 9. Условные распределенияПусть (ξ, η) –
- 66. Нахождение условной функции распределенияУсловная функция распределения случайной величины η при условии, что ξ = x
- 67. Условная плотностьЕсли условная функция распределения случайной величины
- 68. Условное математическое ожиданиеУсловным математическим ожиданием M(η/ξ =
- 69. РегрессияОпределение. Регрессией η на ξ называется случайная
- 70. Корреляционное отношениеКорреляционным отношением η на ξ называется
- 71. Лекция 10. Предельные теоремыНеравенство Маркова. Для
- 72. Сходимость по вероятностиПоследовательность случайных величин ξ1, ξ2
- 73. Закон больших чисел (ЗБЧ)Определение. Говорят, что к
- 74. Закон больших чиселСмысл: среднее значение случайных величин
- 75. ЗБЧ в форме ЧебышеваТеорема. Если для последовательности
- 76. ЗБЧ в форме БернуллиТеорема. Пусть осуществляется серия
- 77. ЗБЧ в форме ХинчинаТеорема. Для того, чтобы
- 78. Центральная предельная теорема (ЦПТ)В теоремах этой группы
- 79. Центральная предельная теорема для независимых одинаково распределенных
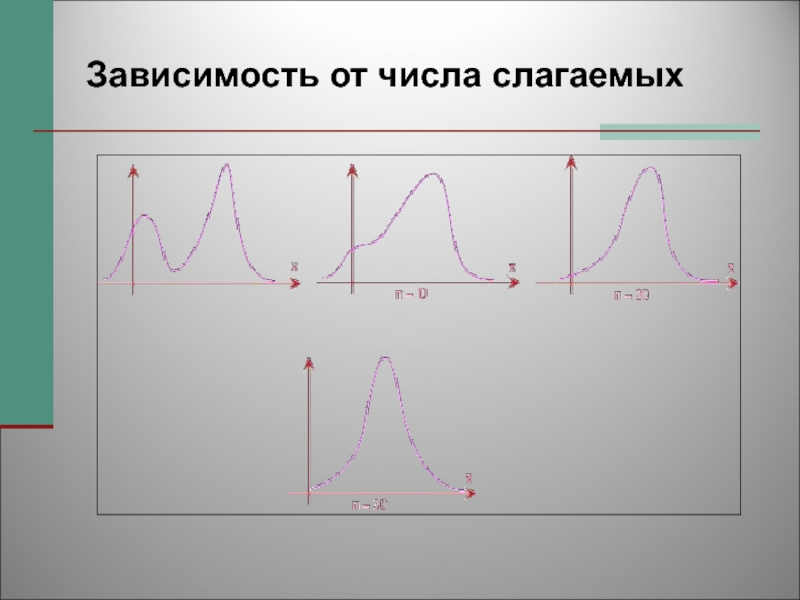
- 80. Зависимость от числа слагаемых
- 81. Практическое значение ЦПТМногие случайные величины можно рассматривать
- 82. Лекция 11. Введение в математическую статистику
- 83. Основные понятия Совокупность наблюдаемых случайных величин Х
- 84. Таким образом, мы рассматриваем генеральную совокупность как
- 85. Эмпирическая функция распределенияЭмпирической функцией распределения называется случайная
- 86. Свойства эмпирической функции распределенияПусть Fn(x) – эмпирическая
- 87. При большом объеме выборки ее элементы объединяют
- 88. Параметры группировкиРазность между максимальным иминимальным элементами выборкиназывается
- 89. Графические характеристики выборки Если на каждом интервале
- 90. Гистограмма и плотностьГистограмма относительных частот является статистическим аналогом плотности распределения генеральной совокупности. СФУ Т.В. Крупкина
- 91. Лекция 12. Числовые характеристики выборки
- 92. Числовые характеристики выборкиВыборочный коэффициент асимметрииВыборочный коэффициент эксцесса Коэффициент вариации Выборочная модаВыборочная медианаВыборочная квантиль порядка q
- 93. Способ получения выборочных формул Чтобы из формулы
- 94. Замечание Если в формуле встречается числовая характеристика,
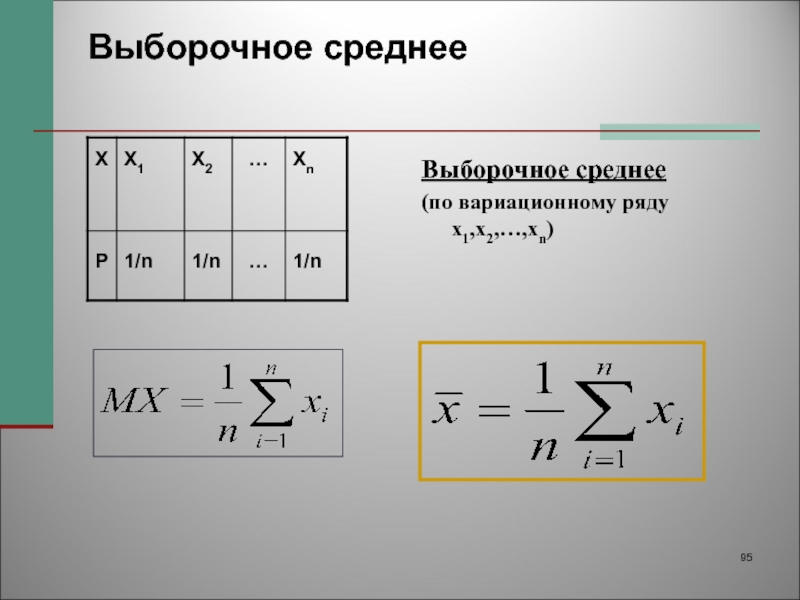
- 95. Выборочное среднее Выборочное среднее(по вариационному ряду x1,x2,…,xn)
- 96. Выборочная дисперсия
- 97. Выборочный начальный момент порядка lТеоретическийВыборочный по вариационному ряду Выборочный по статистическому ряду
- 98. Выборочный центральный момент порядка lТеоретическийВыборочный по вариационному ряду Выборочный по статистическому ряду
- 99. Лекция 13. Распределение выборочных характеристикРаспределением χ2 с
- 100. Плотность распределения χ2 при k = 7
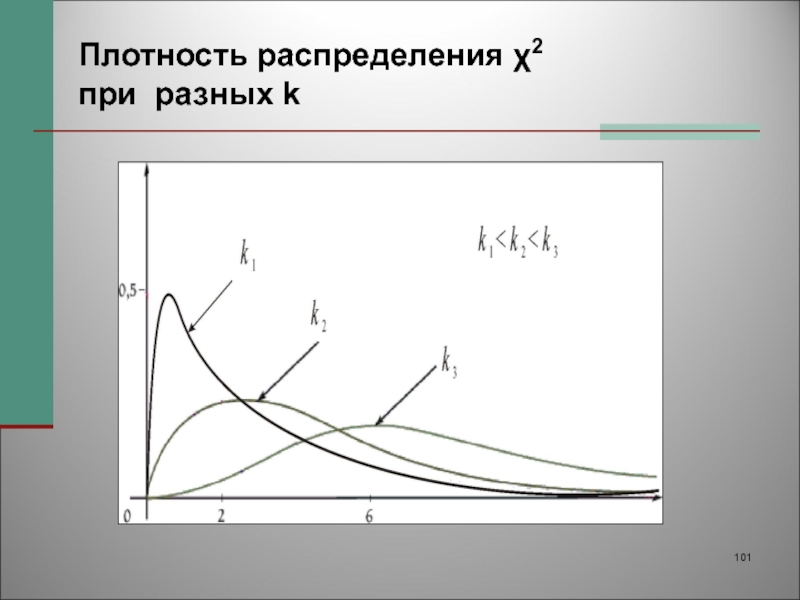
- 101. Плотность распределения χ2 при разных k
- 102. Распределение Стьюдента Распределением Стьюдента с k степенями
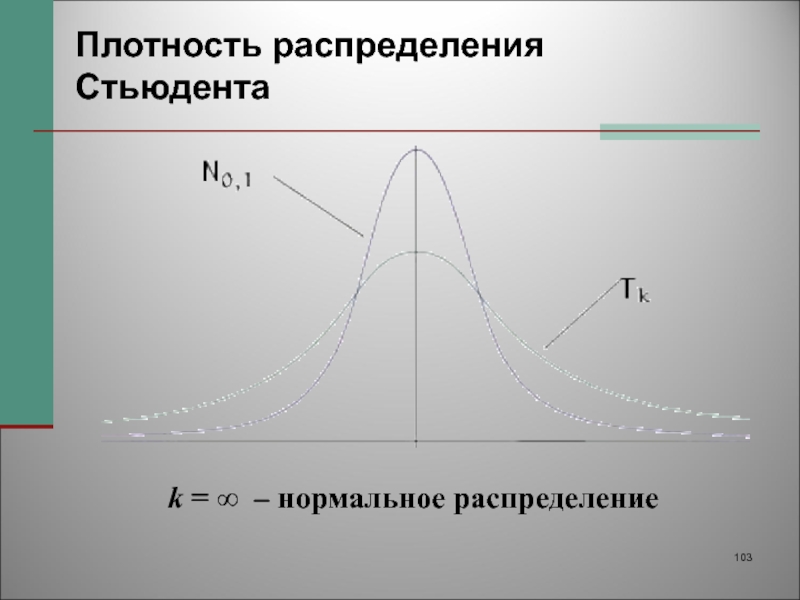
- 103. k = ∞ – нормальное распределениеПлотность распределения Стьюдента
- 104. Распределение Фишера Распределением Фишера с k1 и k2
- 105. Теорема Фишера Пусть (X1, X2,..., Xn) – выборка из N(a, σ). Тогда:
- 106. Теорема Пусть (X1, X2,..., Xn) – выборка из N(a, σ). Тогда:
- 107. Лекция 14. Точечное оценивание параметровОсновная задача математической
- 108. Точечные оценкиРассмотрим параметрическую модель (Fθ) и выборку
- 109. НесмещенностьОценка параметра θ называется несмещенной, еслиДоказывали, что
- 110. Несмещенные оценки в N(a,σ)В N(a,σ):выборочное среднее –
- 111. Состоятельность Оценка параметра θ называется состоятельной, если
- 112. Оптимальность Для параметра θ может быть предложено несколько
- 113. Нижняя граница дисперсий Для дисперсии несмещенной оценки параметра θ выполняется неравенство Рао – Крамера:
- 114. Эффективность Несмещенная оценка параметра θ называется эффективной, если ее дисперсия равна нижней границе Рао –Крамера:
- 115. Оценка максимального правдоподобия Оценкой максимального правдоподобия
- 116. Метод максимального правдоподобия Для нахождения максимума функции
- 117. Метод моментов Теоретические моменты случайной величины
- 118. Лекция 15. Интервальное оценивание параметровДоверительным интервалом уровня значимости α (0< α
- 119. Уровень значимости αЕго обычно берут равным одному
- 120. Схема построения доверительного интервалаНадо взять статистику G(x,
- 121. Доверительный интервал для параметра a распределения N(a, σ)
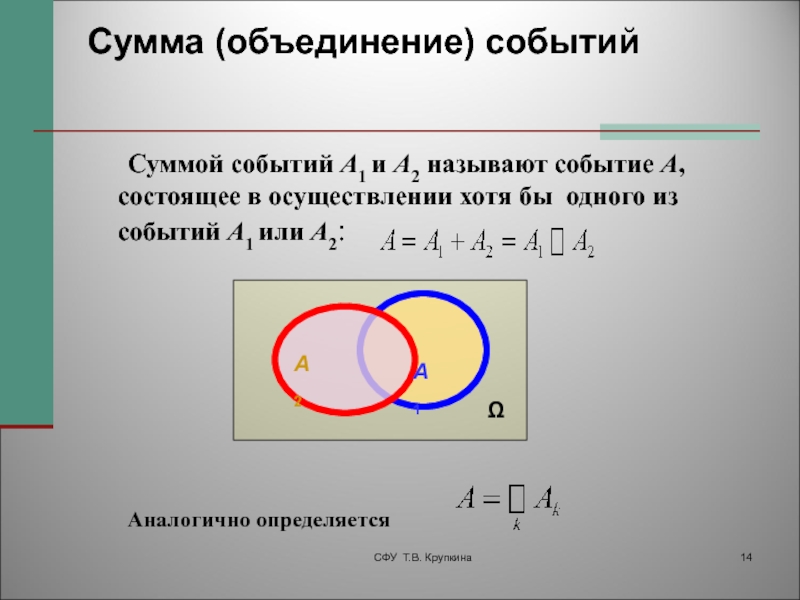
- 122. Квантили нормального распределения
- 123. Доверительный интервал для параметра a (при неизвестном σ) :
- 124. Доверительный интервал для параметра σ распределения N(a, σ)
- 125. Асимптотический доверительный интервалРазрешив неравенство относительно θ, получим доверительный интервал для параметра θ значимости α.
- 126. Лекция 16. Проверка статистических гипотезСтатистической гипотезой называется
- 127. Проверка гипотезыОпределим для малого α >0 область
- 128. Критическая областьСтатистика T(X), определенная выше,называется статистикой критерия,
- 129. Если значение статистики попадает критическую область, то H0 отвергается.
- 130. Ошибка первого родаОшибка первого рода состоит в
- 131. Ошибка второго родаОшибка второго рода состоит в
- 132. Мощность критерияМощностью критерия называется величина М= 1
- 133. Лекция 17. Проверка гипотез о параметрахОбщая схема
- 134. Общая схема проверки параметрических гипотез
- 135. Проверка гипотез о параметрах нормального распределения Гипотезы
- 136. Гипотеза о дисперсии. H0: σ = σ0.
- 137. Гипотеза о среднем. H0: a =
- 138. Гипотеза о среднем. H0: a =
- 139. Гипотеза о дисперсиях. H0: σ1 = σ2. Критерий Фишера
- 140. Гипотеза о средних. H0: a1 = a2. Критерий Стьюдента
- 141. Лекция 18. Проверка гипотез о виде распределения.
- 142. H0: F=F0. Критерий согласия КолмогороваКритерий применяется для
- 143. При n → ∞, если H0 –
- 144. Правило проверкиТаким образом, при заданном уровне значимости
- 145. Критерий согласия Пирсона χ2 Критерий применяется к
- 146. Статистика критерия ПирсонаЕсли для оценки параметров используются оценки максимального правдоподобия, то:
- 147. Правило проверкиν = k – r –1,
- 148. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Лекция 1. Введение в теорию вероятностей
Предметом теории вероятностей является
математический анализ случайных явлений, то есть разработка и применение математического
аппарата для изучения явлений, имеющих случайную природу.Главным обстоятельством, которое определяет границы применимости теории вероятностей, является наличие у изучаемых явлений свойства «статистической устойчивости».
СФУ Т.В. Крупкина
Слайд 3Равновозможные исходы
Рассмотрим некоторый опыт с конечным числом n всевозможных взаимоисключающих
друг друга исходов, которые являются равновозможными. Пусть А – некоторое
событие, связанное с этим исходом.Вероятность p(A) можно определить, как долю тех исходов, в результате которых это событие осуществляется.
СФУ Т.В. Крупкина
Слайд 4Пусть n – число всех исходов, n(A) – число благоприятных
исходов, в результате которых осуществляется событие A.
Классическое определение вероятности
СФУ Т.В.
КрупкинаСлайд 5Формулы комбинаторики
Число перестановок
Число перестановок из n элементов равно
СФУ Т.В.
Крупкина
Слайд 6Выбор без возвращения
Число размещений
С помощью этой формулы можно подсчитать,
сколько существует различных способов выбрать и разместить по различным местам
k из n различных элементов.Формула числа размещений имеет вид:
СФУ Т.В. Крупкина
Слайд 7Выбор без возвращения
Число сочетаний
С помощью этой формулы можно подсчитать, сколько
существует различных способов выбора из n элементов k, не учитывая
порядок элементов в выбранной последовательности. Формула числа сочетаний имеет вид:СФУ Т.В. Крупкина
Слайд 8Статистическое определение вероятности
Пусть рассматриваемый опыт можно повторять многократно, и пусть
N – число всех повторений опыта, а N(А) – число
тех из них, в которых осуществлялось событие А. Отношение N(А)/N называется частотой события А в данной серии испытаний.СФУ Т.В. Крупкина
Слайд 9Статистическое определение вероятности
Практика показывает, что для многих
событий частота при больших
п мало
меняется, колеблясь около некоторого
постоянного значения P*, которое можно
назвать статистической
вероятностью события А,СФУ Т.В. Крупкина
Слайд 10Лекция 2. Основания теории вероятностей
Пространством элементарных исходов Ω называется множество,
содержащее все возможные результаты данного случайного эксперимента, из которых в
эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой ω.СФУ Т.В. Крупкина
Слайд 11
Событиями мы будем называть некоторые наборы элементарных исходов, то есть
подмножества множества Ω. Говорят, что в результате эксперимента произошло событие
A, если в эксперименте произошел один из элементарных исходов, входящих в множество.СФУ Т.В. Крупкина
Слайд 12Элементарные события
Достоверное событие Ω наступает при любом исходе.
Невозможное событие
не может произойти в результате эксперимента, оно не происходит никогда.
Случайное
событие может произойти или не произойти в результате эксперимента, оно происходит иногда.СФУ Т.В. Крупкина
Слайд 13Комбинации событий
Рассмотрим комбинации событий, такие, как
сумма, произведение, разность и
т.д.
Поскольку события – это множества исходов, будем использовать соответствующие определения
для множеств.Сумма событий соответствует объединению множеств, произведение событий соответствует пересечению множеств и т.д.
СФУ Т.В. Крупкина
Слайд 14 Суммой событий A1 и A2 называют событие A, состоящее в
осуществлении хотя бы одного из событий A1 или A2:
Аналогично
определяется Сумма (объединение) событий
A1
A2
Ω
СФУ Т.В. Крупкина
Слайд 15
Противоположным событием к событию A называют событие
состоящее в том, что событие A не произошло:
A
Ω
Противоположное событие
СФУ Т.В.
КрупкинаСлайд 16Вероятность в дискретном пространстве
Чтобы определить вероятность любого события на
дискретном пространстве элементарных исходов, достаточно присвоить вероятность каждому элементарному исходу.
Тогда вероятность любого события определяется как сумма вероятностей входящих в него элементарных исходов.СФУ Т.В. Крупкина
Слайд 17Несчетное множество исходов
Но множество исходов не обязательно конечно или счетно.
Пусть, например, опыт состоит в выборе точки из отрезка [0,
1]. Исходом является любая точка, а множество точек отрезка несчетно. Как ввести вероятность в этом случае?Ответ дает аксиоматика Колмогорова.
СФУ Т.В. Крупкина
Слайд 18Аксиоматическое определение вероятности
Вероятность события есть числовая функция P(A), удовлетворяющая аксиомам:
СФУ Т.В. Крупкина
Слайд 19Лекция 3.
Исчисление вероятностей
Определение
События A и B называются независимыми, если
СФУ Т.В. Крупкина
Слайд 20Условная вероятность
Условной вероятностью события A при условии, что произошло событие
B, называется число
Считают, что
условная вероятность определена только в случае, когда P(B) > 0.
СФУ Т.В. Крупкина
Слайд 22Теорема умножения для двух событий
если соответствующие условные вероятности определены
(то есть если P(A) > 0, P(B) > 0).
Доказательство следует из определения условной вероятности.
СФУ Т.В. Крупкина
Слайд 23Теорема (формула полной вероятности)
Пусть A – случайное событие, H1, H2,
…, Hn – полная группа событий (гипотезы),
Тогда вероятность события А может
быть вычислена по формуле: СФУ Т.В. Крупкина
Слайд 24Теорема (формула Байеса)
Пусть A – случайное событие, H1, H2, …,
Hn – полная группа событий (гипотезы),
Тогда условная вероятность того, что имело
место событие Hk, если наблюдалось событие А, может быть вычислена по формуле: СФУ Т.В. Крупкина
Слайд 25Лекция 4. Схемы испытаний
Схемой испытаний Бернулли называется последовательность независимых
испытаний, в каждом из которых возможны лишь два исхода —
«успех» и «неудача», при этом «успех» в одном испытании происходит с вероятностью p, а «неудача» — с вероятностью q = 1 – p.СФУ Т.В. Крупкина
Слайд 26Теорема (формула Бернулли)
Обозначим через m число успехов в n испытаниях
схемы Бернулли. Тогда
СФУ Т.В. Крупкина
Слайд 27Предельные теоремы для схемы Бернулли
При числе испытаний, превышающем 20, вычисление
точного значения Pn(m) затруднительно. В этих случаях применяют приближенные формулы,
вытекающие из предельных теорем.Различают два случая:
когда р мало, используют приближение Пуассона,
когда р не мало (и не очень близко к единице), справедливо приближение Муавра –Лапласа.
СФУ Т.В. Крупкина
Слайд 28Теорема Пуассона
Если при n → ∞, р → 0
так, что np → λ, 0 < λ < ∞,
то для любого фиксированного m∈N справедливо:СФУ Т.В. Крупкина
Слайд 29Приближенная формула Пуассона
где λ = np. Приближенную формулу Пуассона
применяют при
n > 30,
р < 0.1,
0.1
λ = np < 10. СФУ Т.В. Крупкина
Слайд 30Локальная приближенная формула Муавра –Лапласа
Локальную приближенную формулу Муавра –
Лапласа применяют
при
n > 30, 0.1 ≤ p ≤ 0.9,
nрq > 9. СФУ Т.В. Крупкина
Слайд 33Интегральная приближенная формула Муавра –Лапласа
Интегральную приближенную формулу Муавра –
Лапласа применяют
при n > 30, 0.1 ≤ p ≤ 0.9, nрq >
9.СФУ Т.В. Крупкина
Слайд 35Лекция 5.
Дискретные случайные величины
Пусть есть случайный эксперимент,
Ω ─ пространство элементарных событий.
Определение
Случайной величиной ξ называется
функция, отображающая Ω в R.ξ: Ω → R
(То есть ξ = ξ(ω)).
Смысл: случайная величина – это числовая функция, принимающая значения случайным образом.
СФУ Т.В. Крупкина
Слайд 36Дискретные распределения
Случайная величина ξ имеет дискретное распределение, если она принимает
не более чем счетное число значений.
Значения: a1, a2,…,
Вероятности значений: pi = P(ξ = ai) > 0
СФУ Т.В. Крупкина
Слайд 37Ряд распределения
Если случайная величина ξ имеет дискретное распределение, то
рядом распределения называется соответствие ai ↔pi, которое имеет вид :
СФУ Т.В. Крупкина
Слайд 38Биномиальное распределение B(n, p)
Случайная величина ξ имеет биномиальное распределение с
параметрами n и p, где 0 ≤ p ≤ 1,
если ξ принимает значения 0, 1, 2, …n с вероятностями P{ξ = k} = Cnk pk q n –k.Случайная величина с таким распределением имеет смысл числа успехов в n испытаниях схемы Бернулли с вероятностью успеха p.
СФУ Т.В. Крупкина
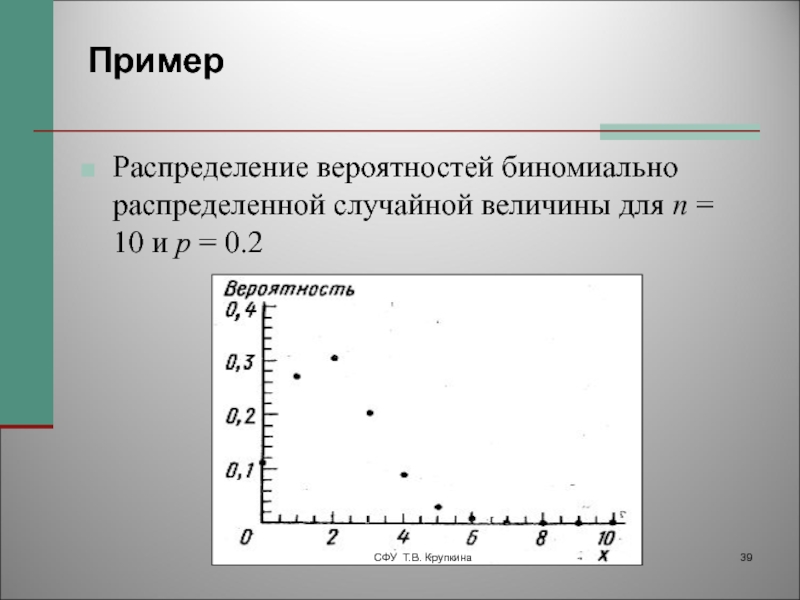
Слайд 39Пример
Распределение вероятностей биномиально распределенной случайной величины для n = 10
и p = 0.2
СФУ Т.В. Крупкина
Слайд 40Распределение Пуассона Pλ
Сл. в. ξ имеет распределение Пуассона с
параметром λ, где λ>0, если ξ принимает значения 0,
1, 2,… с вероятностямиСФУ Т.В. Крупкина
Слайд 41Функция распределения
Определение
Функцией распределения случайной величины ξ называется функция Fξ(x),
при каждом
x∈R равная
Fξ(x) = P{ξ < x}.
СФУ Т.В. Крупкина
Слайд 42Лекция 6.
Непрерывные распределения
Случайная величина ξ имеет непрерывное распределение, если
существует неотрицательная функция fξ(x) такая, что для любого x0∈R функция
распределения представима в видеПри этом функция fξ(x) называется плотностью распределения случайной величины ξ.
СФУ Т.В. Крупкина
Слайд 46Нормальное распределение N (a,σ)
Графики нормальных плотностей имеют симметричную, колоколообразную форму.
а – это величина, которая характеризует положение кривой плотности на
оси абсцисс. Изменение σ приводит к изменению формы кривой плотности, с увеличением σ кривая делается менее островершинной и более растянутой вдоль оси абсцисс.
СФУ Т.В. Крупкина
Слайд 49Многомерные СВ
n – мерной случайной величиной ξ называется вектор ξ(ω)=(ξ1(ω),
ξ2(ω), … , ξn(ω)),
компонентами которого являются одномерные случайные величины.
Функцией распределения
n–мерной случайной величины ξ называется функция Fξ1,ξ2,…,ξn(x1, x2, …, xn)= P(ξ1 < x1, …, ξn < xn)
СФУ Т.В. Крупкина
Слайд 50Лекция 7.
Числовые характеристики
Математическим ожиданием Mξ сл. вел. ξ с
дискретным распределением, задаваемым законом распределения P(ξ=xi) = pi, называется число
Смысл: Математическое ожидание – это среднее значение случайной величины.
СФУ Т.В. Крупкина
Слайд 51
Математическим ожиданием Mξ непрерывно распределенной сл. в. ξ
с с плотностью распределения fξ(x) называется число
Математическое ожидание существует,
если M|ξ| < ∞.
Математическое ожидание н.сл.в.
Слайд 53Дисперсия случайной величины
Если случайная величина ξ имеет математическое ожидание M
ξ , то дисперсией случайной величины ξ называется величина
D ξ = M(ξ - M ξ )2. Смысл: Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
Слайд 55Начальные и центральные моменты
Начальным моментом k-го порядка случайной величины
ξ называется величина
αk = Mξ k.
Центральным моментом k-го порядка
случайной величины ξ называется величина μk, определяемая формулой μk = M(ξ - Mξ )k.
Слайд 59Лекция 8. Линейная зависимость
Определение. Ковариацией случайной величины (ξ, η) называется
центральный смешанный момент второго порядка
Kξ,η = cov(ξ, η) =
M[(ξ – Mξ)∙(η – Mη)]. Ковариация есть мера линейной зависимости между ξ, η. Вычисляется по формуле
cov(ξ, η) = M(ξ∙η) – M ξ∙M η.
Слайд 60Коэффициент корреляции
Коэффициентом корреляции между случайными величинами ξ, η называется
число
Слайд 61Свойства коэффициента корреляции
1. │ρξη│≤ 1.
2. Если ξ,η независимы, то ρξη=
0.
Если │ρξη│=1, то ξ, η линейно зависимы,
то
есть существуют такие a и b, что ξ = aη + b.
Слайд 62Смысл коэффициента корреляции
Коэффициент корреляции есть мера линейной зависимости между
ξ, η.
Его модуль указывает на силу линейной связи
(чем ближе к 1, тем сильнее), а знак указывает на направление связи.
Слайд 63Уравнение линейной регрессии
Уравнением линейной регрессии η на ξ называется уравнение
ηˆ = aξ + b, параметры которого минимизируют остаточную дисперсию
S2ост= M (η – ηˆ)2 = M(η – (aξ + b))2.
Смысл. Уравнение линейной регрессии η на ξ выражает линейную зависимость η от ξ.
Слайд 65Лекция 9. Условные распределения
Пусть (ξ, η) – двумерная случайная величина.
Рассмотрим распределение η при условии, что ξ = x. Оно
называется условным.Определение. Условной функцией распределения случайной величины
η при условии, что ξ = x, называется
Fη/ξ = x = P(η < y/ξ = x).
Слайд 66 Нахождение условной функции распределения
Условная функция распределения случайной величины η
при условии, что ξ = x
Слайд 67Условная плотность
Если условная функция распределения случайной величины η при условии,
что ξ = x, непрерывна, то производная от нее называется
условной плотностью распределения случайной величины η при условии, что ξ = x.Слайд 68Условное математическое ожидание
Условным математическим ожиданием
M(η/ξ = x) случайной
величины η при условии, что ξ = x, называется
математическое ожидание, найденное с помощью условного закона распределения.Условная функция распределения, условная плотность, условное математическое ожидание обладают свойствами функции распределения, плотности, математического ожидания соответственно.
Слайд 69Регрессия
Определение. Регрессией η на ξ называется случайная величина r(ξ), равная
при каждом x условному математическому ожиданию случайной величины η при
условии, что ξ = x.Определение. Линией регрессии называется линия y = r(x), где
r(x) = M(η/ξ = x).
Слайд 70Корреляционное отношение
Корреляционным отношением η на ξ называется числовая характеристика, равная
Смысл: корреляционное отношение измеряет силу зависимости η от ξ
Слайд 71Лекция 10. Предельные теоремы
Неравенство Маркова. Для любого ε >
0
Неравенство Чебышева. Для любого ε > 0
Слайд 72Сходимость по вероятности
Последовательность случайных величин
ξ1, ξ2 ,…, ξn сходится
по вероятности
к сл. в. ξ,
если для любого
ε > 0
Слайд 73Закон больших чисел (ЗБЧ)
Определение. Говорят, что к последовательности случайных величин
ξ1, ξ2 ,…, ξn с математическими ожиданиями
Mξi = ai,
i = 0,1,…,n, применим закон больших чисел, если
Слайд 74Закон больших чисел
Смысл: среднее значение случайных величин стремится по вероятности
к среднему их математических ожиданий (то есть к постоянной величине).
Замечание.
ЗБЧ справедлив при некоторых условиях. Различные группы условий определяют разные формы закона больших чисел.
Слайд 75ЗБЧ в форме Чебышева
Теорема. Если для последовательности случайных величин {ξn}
с математическими ожиданиями Mξi=ai
и с
дисперсиями Dξi=σ2i, i=0,1,…,n, выполняются условия:сл.в. {ξn} независимы;
дисперсии всех сл.в. {ξn} ограничены одним и тем же числом, (σ2i ≤ A для всех i),
то к {ξn} применим ЗБЧ.
Слайд 76ЗБЧ в форме Бернулли
Теорема. Пусть осуществляется серия из n независимых
опытов, проводимых по схеме Бернулли с параметром p, пусть m
– число успехов, m/n – частота успехов в данной серии испытаний. ТогдаСлайд 77ЗБЧ в форме Хинчина
Теорема. Для того, чтобы к последовательности
случайных величин
{ξn} был применим ЗБЧ,
достаточно выполнения условий:
сл.в. {ξn} независимы;
сл.в. {ξn} одинаково
распределены.Тогда
Слайд 78Центральная предельная теорема (ЦПТ)
В теоремах этой группы выясняются условия, при
которых возникает нормальное распределение. Общим для этих теорем является следующее
обстоятельство: закон распределения суммы достаточно большого числа независимых случайных величин при некоторых условиях неограниченно приближается к нормальному.Слайд 79Центральная предельная теорема для независимых одинаково распределенных сл. в.
Если случайные
величины {ξn} независимы, одинаково распределены и имеют конечные математические ожидания
Mξi=a и дисперсии Dξi=σ2,… i=0,1,…,n, то при n→∞Слайд 81Практическое значение ЦПТ
Многие случайные величины можно рассматривать как сумму отдельных
независимых слагаемых.
Например: числа продаж некоторого товара;
объемы прибыли от
реализации однородного товара различными производителями; валютные курсы.
Из ЦПТ следует, что они приближенно нормально распределены.
Слайд 82
Лекция 11. Введение в математическую статистику
Математическая статистика – это раздел
математики который занимается разработкой методов сбора, описания и анализа экспериментальных
результатов наблюдений, массовых случайных явлений.Фундаментальными понятиями математической статистики являются генеральная совокупность и выборка.
СФУ Т.В. Крупкина
Слайд 83Основные понятия
Совокупность наблюдаемых случайных величин Х = (Х1, ...,
Хn) называется выборкой, сами величины Xi , i =1,..., n,
– элементами выборки, а их число n – ее объемом.Реализации выборки Х будем обозначать строчными буквами х = (x1,..., xn).
Статистической моделью
Слайд 84Таким образом, мы рассматриваем генеральную совокупность как случайную величину ξ,
а выборку – как n – мерную случайную величину
(ξ1, …, ξn), компоненты которой независимы и одинаково распределены (так же, как ξ).Такие выборки называются простыми.
Простая выборка
Слайд 85Эмпирическая функция распределения
Эмпирической функцией распределения называется случайная функция от Fn(x),
вычисляемая по формуле
где νn – число элементов выборки Х, значения
которых меньше х.
Слайд 86Свойства эмпирической функции распределения
Пусть Fn(x) – эмпирическая функция распределения, построенная
по выборке Х из распределения ξ, и Fξ(x) – соответствующая
теоретическая функция.Тогда:
Слайд 87 При большом объеме выборки ее элементы объединяют в группы, представляя
результаты опытов в виде группированного статистического ряда.
Для этого интервал,
содержащий все элементы выборки, разбивается на k непересекающихся интервалов длины h. Результаты сводятся в таблицу, называемую таблицей частот группированной выборки.Группировка выборки
Слайд 88Параметры группировки
Разность между максимальным и
минимальным элементами выборки
называется размахом выборки R.
Число
интервалов k находится из условия
2k –1 ≈ n,
где
n – объем выборки. Длину интервала h находят по формуле
h = R/k.
Все интервалы имеют одинаковую длину.
Слайд 89Графические характеристики выборки
Если на каждом интервале построить прямоугольник с
высотой ni/h, получим гистограмму.
Кривая, соединяющая середины верхних оснований
гистограммы, называется полигоном (частот). Полигон — непрерывная функция (ломаная).
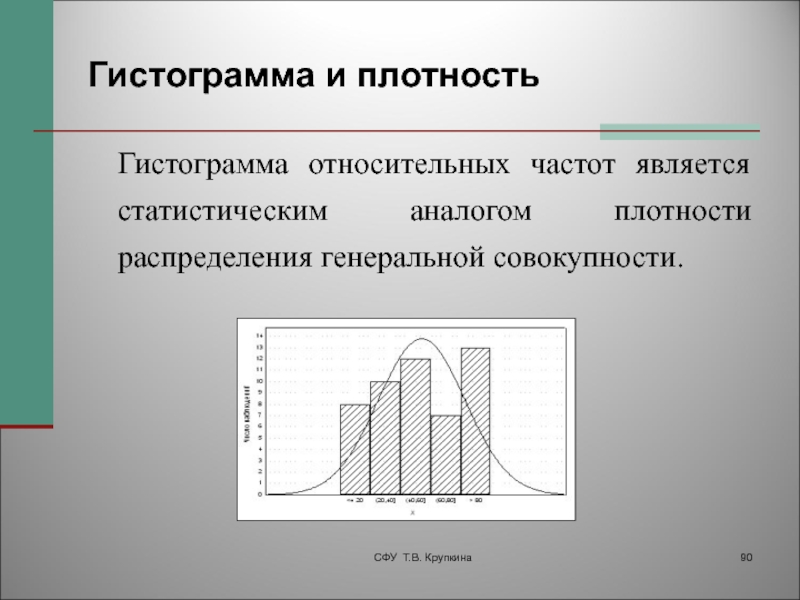
Слайд 90Гистограмма и плотность
Гистограмма относительных частот является статистическим аналогом плотности распределения
генеральной совокупности.
СФУ Т.В. Крупкина
Слайд 91
Лекция 12.
Числовые характеристики выборки
Выборочное среднее
Выборочная дисперсия
Выборочная исправленная дисперсия
Выборочное среднеквадратическое
отклонение
Выборочный начальный момент порядка l
Выборочный центральный момент
порядка l
СФУ
Т.В. КрупкинаСлайд 92Числовые характеристики выборки
Выборочный коэффициент асимметрии
Выборочный коэффициент эксцесса
Коэффициент вариации
Выборочная
мода
Выборочная медиана
Выборочная квантиль порядка q
Слайд 93Способ получения выборочных формул
Чтобы из формулы числовой характеристики сл.в.
получить формулу выборочной характеристики, нужно:
заменить обозначение сл.в. обозначением элемента выборки
(xi)заменить знак математического ожидания М[..] на
Слайд 94Замечание
Если в формуле встречается числовая характеристика, для которой уже
известна соответствующая ей выборочная, то числовая характеристика заменяется на выборочную.
Например,
Слайд 97Выборочный начальный момент порядка l
Теоретический
Выборочный по вариационному ряду
Выборочный по
статистическому ряду
Слайд 98Выборочный центральный момент порядка l
Теоретический
Выборочный по вариационному ряду
Выборочный по
статистическому ряду
Слайд 99Лекция 13. Распределение выборочных характеристик
Распределением χ2 с k степенями свободы
называется распределение случайной величины χ2(k), равной сумме квадратов k независимых
нормально распределенных по закону N(0,1) случайных величин Ui i = 1,2,…,k, то есть распределение случайной величиныСлайд 102Распределение Стьюдента
Распределением Стьюдента с k степенями свободы называется распределение
случайной величины Т(k), равной
где U имеет нормальное распределение N(0, 1).
Величина, имеющая распределение Стьюдента с k степенями свободы будет также обозначаться t(k). Слайд 104Распределение Фишера
Распределением Фишера с k1 и k2 степенями свободы называется
распределение случайной величины F(k1, k2), равной
Слайд 107Лекция 14. Точечное оценивание параметров
Основная задача математической статистики состоит в
нахождении распределения наблюдаемой случайной величины Х по данным выборки. Во
многих случаях вид распределения Х можно считать известным, и задача сводится к получению приближенных значений неизвестных параметров этого распределения.Слайд 108Точечные оценки
Рассмотрим параметрическую модель (Fθ) и
выборку (X1, X2,..., Xn)
. (То есть известен вид функции распределения F, и F
зависит от одного неизвестного параметра θ).Точечной оценкой неизвестного параметра θ
называется функция элементов выборки,
используемая для получения приближенного
значения θ.
Слайд 109Несмещенность
Оценка параметра θ называется несмещенной, если
Доказывали, что
Значит, в любом распределении, у которого математическое ожидание равно параметру, выборочное среднее есть несмещенная оценка этого параметра.
Слайд 110Несмещенные оценки в N(a,σ)
В N(a,σ):
выборочное среднее – несмещенная оценка параметра
a,
выборочная дисперсия – смещенная оценка σ2,
исправленная
выборочная дисперсия – несмещенная оценка σ2. Слайд 112Оптимальность
Для параметра θ может быть предложено несколько несмещенных оценок. Мерой
точности несмещенной оценки считают ее дисперсию
Несмещенная оценка параметра
θ называется оптимальной, если она имеет минимальную дисперсию среди всех несмещенных оценок этого параметра. Слайд 113Нижняя граница дисперсий
Для дисперсии несмещенной оценки
параметра
θ выполняется неравенство Рао – Крамера:
Слайд 114Эффективность
Несмещенная оценка параметра θ называется эффективной, если ее дисперсия равна
нижней границе Рао –Крамера:
Слайд 115Оценка максимального правдоподобия
Оценкой максимального правдоподобия (о.м.п.) неизвестного параметра
θ называют значение, при котором функция правдоподобия достигает максимума
(как функция от θ при фиксированных (X1, X2,..., Xn). Это значение параметра зависит от выборки и является искомой оценкой.Слайд 116Метод максимального правдоподобия
Для нахождения максимума функции правдоподобия L можно
искать максимум
ln L и решать уравнение
правдоподобияСлайд 117Метод моментов
Теоретические моменты случайной величины зависят от
параметра, а выборочные моменты зависят от элементов выборки. Но выборочные
приближенно равны теоретическим. Приравняем их, и получим уравнения, связывающие параметр и элементы выборки. Выразим из них параметр. Полученная функция и называется оценкой метода моментов (о.м.м.).Слайд 118Лекция 15. Интервальное оценивание параметров
Доверительным интервалом уровня значимости α (0
α
которого выполняется условие:P(I1(X) ≤ θ ≤ I2 (X)) = 1 – α.
Число 1 – α называется доверительной вероятностью, а I1(X), I2 (X)
– нижней и верхней доверительными границами.
СФУ Т.В. Крупкина
Слайд 119Уровень значимости α
Его обычно берут равным одному из чисел 0.001,
0.005, 0.01, 0.05, 0.1. Уровень значимости выражает ошибку доверительного интервала.
Чем меньше α, тем больше доверительная вероятность и тем надежнее доверительный интервал, но более надежный интервал является более широким и менее информативным. Стандартный уровень значимости α =0.05. Соответствующий доверительный интервал называется 95% –м.Слайд 120Схема построения доверительного интервала
Надо взять статистику G(x, θ), такую, что
она сама зависит от параметра θ, а ее распределение от
θ не зависит, записать уравнениеP(γ1 ≤ G(x, θ) ≤ γ2) = 1 – α,
и разрешить неравенство под знаком вероятности относительно параметра θ.
Слайд 125Асимптотический доверительный интервал
Разрешив неравенство относительно θ, получим доверительный интервал для
параметра θ значимости α.
Слайд 126Лекция 16. Проверка статистических гипотез
Статистической гипотезой называется утверждение о виде
распределения генеральной совокупности.
Проверяемая гипотеза называется нулевой и обозначается
H0. Наряду с ней рассматривают альтернативную гипотезу H1.Правило, согласно которому проверяют гипотезу H0 (принимают или отвергают), называется статистическим критерием.
Слайд 127Проверка гипотезы
Определим для малого α >0 область V так, чтобы
в случае справедливости гипотезы H0 вероятность осуществления события P(T(x) €
V ) = α.По выборке вычислим значение статистики Т = tв.
Если окажется, что tв € V, то в предположении справедливости гипотезы H0, произошло маловероятное событие и эта гипотеза должна быть отвергнута как противоречащая статистическим данным. В противном случае нет основания отказываться от гипотезы H0 .
Слайд 128Критическая область
Статистика T(X), определенная выше,
называется статистикой критерия, V –
критической областью
критерия, α – уровнем
значимости критерия (вероятностью
ошибочного отвержения гипотезы
H0, когда она верна).
В конкретных задачах величину α берут
равной 0,005; 0,01; 0,05; 0,1.
Слайд 130Ошибка первого рода
Ошибка первого рода состоит в том, что H0
отвергается, когда она верна.
Вероятность ошибки 1 – го рода
обозначается α, α=P(T€ V/ H0) (значение статистики Т
принадлежит критической области V при
условии, что верна H0) .
α – это уровень значимости.
Слайд 131Ошибка второго рода
Ошибка второго рода состоит в том, что H0
не отвергается, когда она не верна.
Вероятность ошибки 2 –
го рода обозначается β. β – это вероятность того, что значение
статистики Т не принадлежит критической
области V при условии, что верна H1.
Слайд 132Мощность критерия
Мощностью критерия
называется величина М= 1 – β.
Мощность
критерия М равна вероятности отвергнуть H0,
когда она не
верна. М – это вероятность того, что значение
статистики Т принадлежит критической
области V при условии, что верна H1.
Слайд 133Лекция 17. Проверка гипотез о параметрах
Общая схема проверки
1.Сформулировать статистическую
параметрическую
модель, нулевую и
альтернативную гипотезы, задать уровень
значимости α.
2. Выбрать
статистику Т, такую, что она сама зависит от параметра θ, а ее распределение
от θ не зависит, и различается при H0 и при H1.
СФУ Т.В. Крупкина
Слайд 134
Общая схема проверки параметрических гипотез
3. Найти критическую область V.
4.
Рассчитать по выборке значение ст –ки Тв.
5. Если Тв попадает
в критическую область V, то нулевая гипотеза отвергается (в пользу альтернативной). Если Тв не попадает в критическую область V, то нулевая гипотеза не отвергается.6. Сформулировать ответ в терминах вопроса.
Слайд 135Проверка гипотез о параметрах
нормального распределения
Гипотезы о параметрах одного распределения
(одна выборка).
Гипотезы о параметрах двух распределений (две независимые
выборки).Гипотезы о параметрах двух распределений (две парные выборки).
Слайд 137Гипотеза о среднем. H0: a = a0.
1) (X1,, X2,...,Xn)
€, N(θ1, σ), то есть параметр σ известен, а параметр
a не известен.Слайд 138Гипотеза о среднем. H0: a = a0.
2) (X1,, X2,...,
Xn) € N(θ1,θ2), то есть оба параметра неизвестны.
Слайд 141Лекция 18. Проверка гипотез о виде распределения.
Критерии согласия
Критериями согласия
называют
критерии, предназначенные для проверки
простой гипотезы H0: F = F0,
при сложнойальтернативной H1: F ≠ F0.
Для проверки гипотезы возьмем статистику
T = T(X), характеризующую отклонение
эмпирических данных от соответствующих
гипотезе теоретических значений.
Слайд 142H0: F=F0. Критерий согласия Колмогорова
Критерий применяется для непрерывных сл.в.
В качестве
статистики T выбирают величину
Dn = Dn(x) = max|Fn(x) –
F0(x)|,где Fn(x) – эмпирическая функция распределения, а в качестве критической области – область вида V = (t*,+∞).
Слайд 143При n → ∞, если H0 – верная гипотеза,
распределение
статистики √n Dn сходится к
функции Колмогорова К(t). Функция
Колмогорова
задается таблично. При практических расчетах значения К(t) можно
применять уже при n > 20.
t* находится из таблиц К(t) по заданному α.
Например, при α = 0,05 находим, что t* = 1,358.
Применение критерия Колмогорова
Слайд 144Правило проверки
Таким образом, при заданном уровне
значимости α правило проверки
гипотезы
H0 при n>20 сводится к
следующему:
если значение статистики √n Dn ≥
t*, то H0 отвергают, в противном случае
делают вывод, что статистические
данные не противоречат гипотезе.
Слайд 145Критерий согласия Пирсона χ2
Критерий применяется к группированной выборке.
Пусть n
– объем выборки (n ≥ 50),
k – число интервалов
группировки, ni – число значений, попавших в i –й интервал,
i = 1,…,k, (ni ≥ 5),
pi – теоретическая вероятность попадания одного элемента выборки в i – й интервал,
npi = niТ ( теоретические частоты).
Слайд 146Статистика критерия Пирсона
Если для оценки параметров используются оценки максимального правдоподобия,
то:
Слайд 147Правило проверки
ν = k – r –1, где r –
число параметров, оцененных
по выборке.
Критическая область имеет вид (t*, +∞),
где t* – квантиль распределения χ2 порядка 1 – α.
Если значение статистики T ≥ t*, то H0
отвергают, в противном случае делают
вывод, что статистические данные не
противоречат гипотезе.





































![Теория вероятностей и математическая статистика Равномерное распределение R [a, b] СФУ Т.В. Крупкина Равномерное распределение R [a, b] СФУ Т.В. Крупкина](/img/thumbs/9536c1e313f0c547635e16cda392597c-800x.jpg)