Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Содержание
- 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
- 2. Теория вероятностей?ОГЭ
- 3. Теория вероятностей – раздел математики, изучающий закономерности
- 4. Презентация проекта «История возникновения теории вероятностей»План сообщения:1.
- 5. История возникновения теории вероятностей Возникновение
- 6. Самые ранние работы учёных в
- 7. Под влиянием поднятых и рассматриваемых
- 8. Его работа, в которой вводятся
- 9. Важный вклад в теорию вероятностей
- 10. В первой половине XIX века
- 11. Во второй половине XIX века основной
- 12. Современный вид теория вероятностей получила
- 13. Вероятность случайного события Вероятностью события А
- 14. ЗАДАЧА НА ОПРЕДЕЛЕНИЕ КЛАССИЧЕСКОЙ ВЕРОЯТНОСТИ В сборнике
- 15. Решите самостоятельно: В сборнике билетов по
- 16. Основные виды задач
- 17. 1 вид. В соревнованиях по толканию ядра
- 18. В соревновании по толканию ядра участвуют 4
- 19. 2 вид. Фабрика выпускает сумки. В среднем
- 20. Фабрика выпускает сумки. В среднем на 80
- 21. 3 вид. В сборнике билетов по биологии
- 22. В сборнике билетов по математике всего 20
- 23. 4 вид. В среднем из 2000 садовых
- 24. В среднем из 1000 садовых насосов, поступивших
- 25. Теория вероятностей?вид задачи
- 26. ТЕСТ1. Выбери классическое определение вероятности события:
- 27. 2. Из кармана на пол выпала монета.
- 28. 3. Посеяли 100 семян. Из них взошли
- 29. 4. В коробке находятся 500 деталей, из
- 30. 5. В магазине на складе находятся 100
- 31. Ответы
- 32. Что узнали нового?Что вам не понравилось?Что вас поразило?Что хотите узнать нового?
- 33. Удачи на ОГЭ!
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Теория вероятностей – раздел математики, изучающий закономерности случайных явлений: случайные
события, случайные величины, их свойства и операции над ними
Слайд 4Презентация проекта
«История возникновения теории вероятностей»
План сообщения:
1. Первые попытки математического анализа
азартных игр
2. Работы учёных в области теории вероятностей:
а) Блез Паскаль
и Пьер Фермаб) Христиан Гюйгенс
в)Якоб Бернулли
г)Лаплас и Пуассон
д) П.Л.Чебышев, А.А.Марков и А.М.Ляпунов
е) А.Н.Колмогоров Подготовила:
Аделова А.
Слайд 5История возникновения теории вероятностей
Возникновение теории вероятностей как науки
относят к средним векам и первым попыткам математического анализа азартных
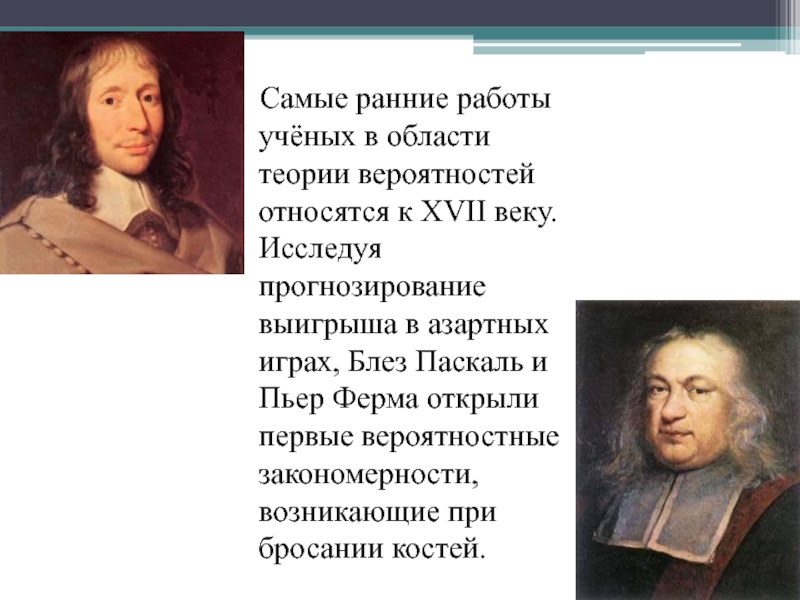
игр (орлянка, кости, рулетка). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмперическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях.Слайд 6 Самые ранние работы учёных в области теории вероятностей
относятся к XVII веку. Исследуя прогнозирование выигрыша в азартных играх,
Блез Паскаль и Пьер Ферма открыли первые вероятностные закономерности, возникающие при бросании костей.Слайд 7 Под влиянием поднятых и рассматриваемых ими вопросов решением
тех же задач занимался и Христиан Гюйгенс. При этом с
перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно.Слайд 8 Его работа, в которой вводятся основные понятия теории
вероятностей (понятие вероятности как величины шанса; математическое ожидание для дискретных
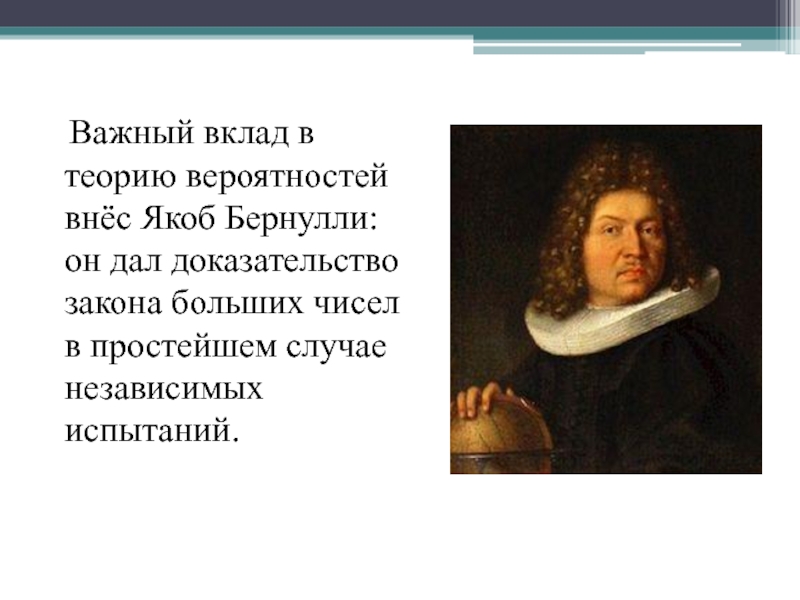
случаев, в виде цены шанса), а также используются теоремы сложения и умножения вероятностей (не сформулированные явно), вышла в печатном виде на двадцать лет раньше (1657 год) издания писем Паскаля и Ферма (1679 год).Слайд 9 Важный вклад в теорию вероятностей внёс Якоб Бернулли:
он дал доказательство закона больших чисел в простейшем случае независимых
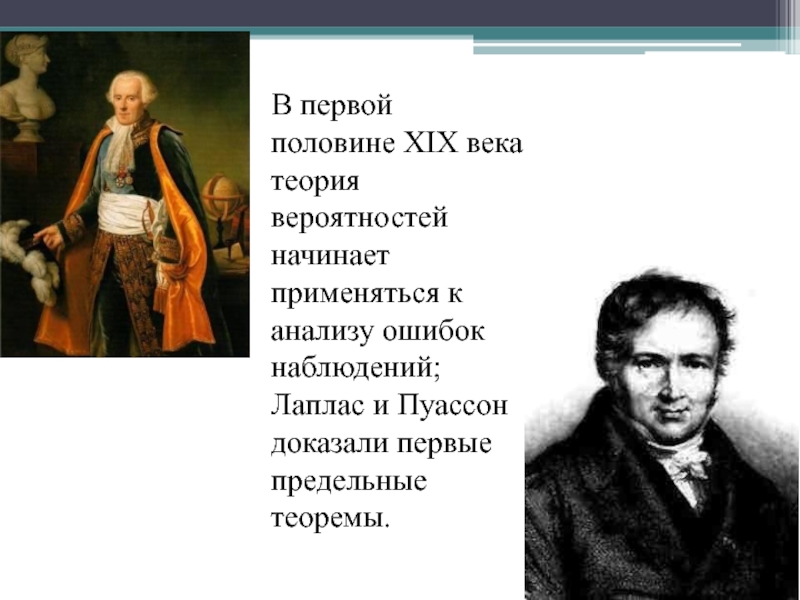
испытаний.Слайд 10 В первой половине XIX века теория вероятностей начинает
применяться к анализу ошибок наблюдений; Лаплас и Пуассон доказали первые
предельные теоремы.Слайд 11 Во второй половине XIX века основной вклад внесли русские
учёные П.Л.Чебышев, А.А.Марков и А.М.Ляпунов. В это время были доказаны
закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова.Слайд 12 Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной
Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический
вид и окончательно стала восприниматься как один из разделов математики.Слайд 13Вероятность случайного события
Вероятностью события А называется отношение числа m благоприятных
для этого события исходов к n числу всех равновозможных исходов
Вероятность
выражают в процентахВероятность события обозначается большой латинской буквой Р (от французского слова probabilite, что означает – возможность, вероятность)
Слайд 14ЗАДАЧА НА ОПРЕДЕЛЕНИЕ КЛАССИЧЕСКОЙ ВЕРОЯТНОСТИ В сборнике билетов по физике всего
50 билетов, в 12 из них встречается вопрос по конденсаторам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по конденсаторам.Решение:
N(A) =50-12=38 –билетов без конденсаторов
N=50 –всего билетов
Р(А)= =0,76 Ответ: 0,76
Слайд 15Решите самостоятельно: В сборнике билетов по химии всего 35 билетов, в
7 из них встречается вопрос по кислотам. Найдите вероятность того,
что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.Ответ: 0,8
Слайд 171 вид. В соревнованиях по толканию ядра участвуют 9 спортсменов
из Дании, 3 спортсмена из Швеции, 8 спортсменов из Норвегии
и 5 — из Финляндии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из ФинляндииРешение
Всего участвует N = 9+3+8+5=25 спортсменов.
А т.к. финнов N(A) = 5 человек, то вероятность того, что на последнем месте будет спортсмен из Финляндии
P = = 0,2
Слайд 18В соревновании по толканию ядра участвуют 4 спортсмена из Македонии,
9 спортсменов из Сербии, 7 спортсменов из Хорватии и 5
– из Словении. Порядок в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из МакедонииN(A) = 4
N = 25
P = = 0,16
Слайд 192 вид. Фабрика выпускает сумки. В среднем на 180 сумок
приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что
купленная сумка окажется качественной. Результат округлите до сотых.Решение
N(A) = 180-8 = 172 сумки качественные,
N= 180 всего сумок
P = = 0,955...≈ 0,96
Слайд 20Фабрика выпускает сумки. В среднем на 80 качественных сумок приходится
8 сумок со скрытыми дефектами. Найдите вероятность того, что купленная
сумка окажется качественной.N(A) = 80
N = 80+8=88
P = = 0,91
Слайд 213 вид. В сборнике билетов по биологии всего 35 билетов,
в 14 из них встречается вопрос по зоологии. Найдите вероятность
того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по зоологии.Решение
N(A) = 35-14=21- билет без зоологии
N= 35 – всего билетов
Вероятность равна
P = =0,6
Слайд 22В сборнике билетов по математике всего 20 билетов, в 13
из них встречается вопрос по производной. Найдите вероятность того, что
в случайно выбранном на экзамене билете школьнику не достанется вопроса по производнойN(A) = 20 – 13 = 7
N = 20
P = = 0,35
Слайд 234 вид. В среднем из 2000 садовых насосов, поступивших в
продажу, 12 подтекают. Найдите вероятность того, что один случайно выбранный
для контроля насос не подтекает.Решение
N(A) = 2000-12=1988 - насосов не подтекает
N= 2000 – всего насосов
Вероятность, что случайно выбранный насос не подтекает:
P = =0,994
Слайд 24В среднем из 1000 садовых насосов, поступивших в продажу, 4
подтекают. Найдите вероятность того, что один случайно выбранный для контроля
насос не подтекаетN(A) = 1000 – 4 = 996
N = 1000
P = = 0,996
Слайд 26ТЕСТ
1. Выбери классическое определение вероятности события:
Вероятность события -
1. это
отношение числа благоприятных для события исходов испытания к числу всех
равновероятных исходов.2. это отношение числа неблагоприятных для события исходов испытания к числу всех равновероятных исходов.
3. это отношение числа всех исходов испытания к числу благоприятных для события исходов.
4. это отношение числа всех исходов испытания к числу неблагоприятных для события исходов
Слайд 272. Из кармана на пол выпала монета. Найти вероятность того,
что выпал "орел":
2
0,5
1
0,2
0,1
Слайд 283. Посеяли 100 семян. Из них взошли 85%. Событие А
= {взошло семечко}. Чему равна вероятность события А?
0,85
85
100/85
185
Слайд 294. В коробке находятся 500 деталей, из которых 7 -
бракованные. Событие В = {наугад из коробки достали бракованную деталь} Чему
равна вероятность события В?500/7
7/500
3500
350
Слайд 305. В магазине на складе находятся 100 лампочек. Из них
10 - не кондиция. Событие С = {наугад достали хорошую лампочку}. Найти
вероятность события С: 0,190
9
0,9