Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей
Содержание
- 1. Теория вероятностей
- 2. Понятие случайной величины.Закон распределения ДСВ.Операции над случайными величинами.Числовые характеристики ДСВ.Математическое ожидание ДСВДисперсия ДСВCреднее квадратическое отклонениеСодержание презентации
- 3. Пример. Вероятность изготовления на автоматическом станке стандартной
- 4. Число появления бракованных деталей можно рассматривать как
- 5. Случайной называют величину, которая в результате испытания
- 6. Понятие случайной величины тесно связано с понятием
- 7. Примеры случайных величин:X – число попаданий при
- 8. Дискретной называют случайную величину, которая принимает отдельные,
- 9. Случайные величины будем обозначать прописными буквами латинского
- 10. Равномерный закон распределенияЗакон распределения Нормальный закон распределенияПример
- 11. Теория вероятностейДискретные случайные величины
- 12. Для дискретной случайной величины закон распределения
- 13. События Х=х1, Х=х2,..., Х=хn состоящие в том,
- 14. Закон распределенияГрафический способ.Графическое изображение ряда распределения называется
- 15. Аналитический способ.Аналитическим выражением закона распределения может быть,
- 16. Пример. Вероятность попадания стрелком в цель равна
- 17. Пример. Найти ряд распределения случайной величины, являющейся
- 18. Построим многоугольник распределения1/81/43/81/20123XPЗакон распределения
- 19. Теория вероятностейОперации над ДСВ
- 20. Две случайные величины называются независимыми, если закон
- 21. Пусть дана случайная величина Х.Произведением k∙Х случайной
- 22. Пример. Пусть дана случайная величина Х:Найти закон
- 23. m-й степенью случайной величины X, т.е.
- 24. Суммой случайных величин X и Y называется
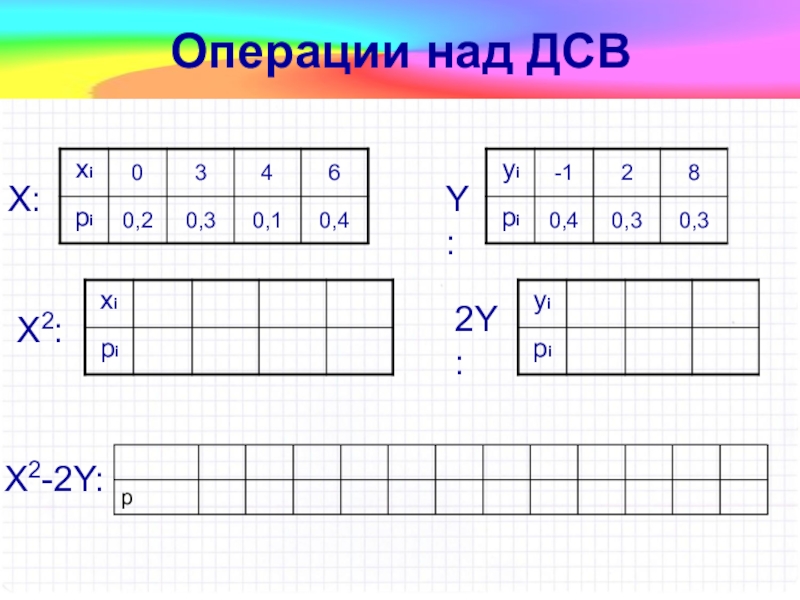
- 25. Операции над ДСВX:Y:X2-2Y:X2:2Y:
- 26. Произведением независимых случайных величин X и Y
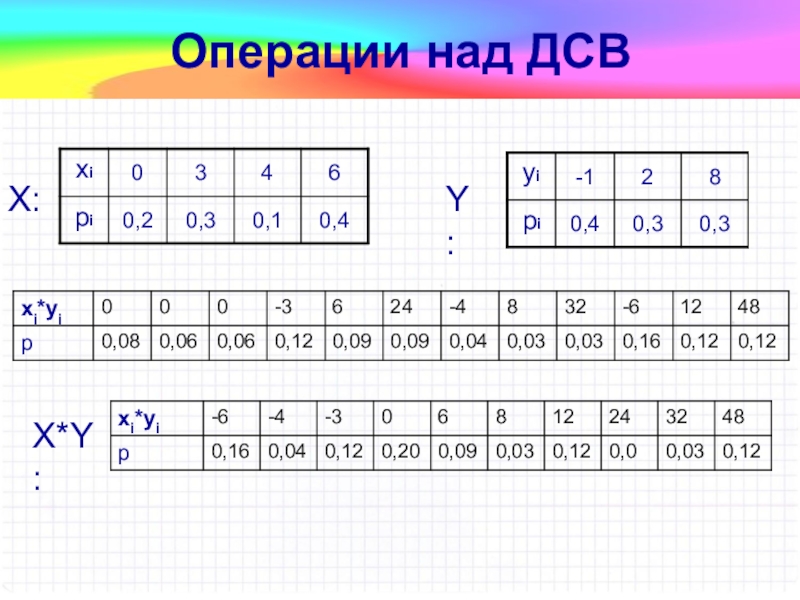
- 27. Операции над ДСВX:Y:X*Y:
- 28. Две ДСВ X и Y заданы своими
- 29. Операции над ДСВПример. Две ДСВ X и
- 30. Операции над ДСВОтвет: X+2Y:*(-3X):
- 31. Теория вероятностейЧисловые характеристики ДСВ
- 32. Задача. Известны законы распределения случайных величин Х
- 33. Математическим ожиданием, или средним значением, М(Х) дискретной
- 34. Решение. По определению математического ожидания: М(Х)=0∙0,15 +
- 35. Решение. Возможные значения случайной величины X -
- 36. т.е. ряд распределения X:Математическое ожидание ДСВНайдем математическое
- 37. Свойства математического ожидания:Математическое ожидание постоянной величины равно
- 38. Пример. Найти математическое ожидание случайной величины Z=
- 39. Пример. Даны распределения случайных величин Х и
- 40. Z=Y-2X
- 41. Пример. В результате обработки данных многолетних наблюдений
- 42. Математическое ожиданиеРешение. 1) Найдем закон распределения ДСВ
- 43. Рассмотрим две ДСВ:X:Y:ДисперсияНайдем математические ожидания этих величин:M(X)
- 44. Пусть X - случайная величина и М
- 45. Пример. Задан закон распределения дискретной случайной величины
- 46. Дисперсией (рассеянием) дискретной случайной величины называют
- 47. Пример. Вычислим дисперсию для ДСВ Х из
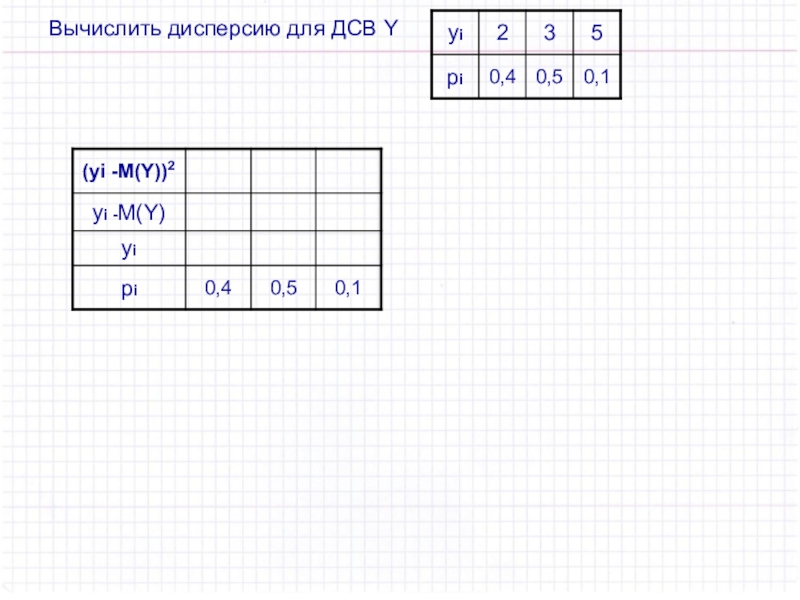
- 48. Вычислить дисперсию для ДСВ Y
- 49. Формула для вычисления дисперсии.Дисперсия равна разности между
- 50. Средним квадратическим отклонением случайной величины X называют
- 51. Свойства дисперсии:Дисперсия постоянной величины С равна нулю:
- 52. Пример. Даны две ДСВ X и Y:
- 53. Пример. Даны две ДСВ X и Y:
- 54. 2) Z =Y-X. Найдем M(Z) и D(Z),
- 55. Слайд 55
- 56. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Понятие случайной величины.
Закон распределения ДСВ.
Операции над случайными величинами.
Числовые характеристики ДСВ.
Математическое
ожидание ДСВ
Слайд 3Пример. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8.
Найти вероятности возможного числа появления бракованных деталей среди 5 отобранных.
Решение. Вероятность изготовления бракованной детали
p = 1 - 0,8 = 0,2.
Искомые вероятности находим по формуле Бернулли:
P5(0)=0,32768; P5(3)=0,0512;
P5(1)=0,4096; P5(4)=0,0064;
P5(2)=0,2048; P5(5)=0,00032.
Полученные вероятности запишем в виде таблицы:
Понятие случайной величины
Слайд 4Число появления бракованных деталей можно рассматривать как некоторую переменную (величину),
которая в результате испытания случайно может принимать одно из своих
значений 0, 1, 2, 3, 4, 5, (какое именно — заранее не известно). Этим значениям соответствую вероятности. Такая величина называется случайной.Понятие случайной величины
Слайд 5Случайной называют величину, которая в результате испытания примет одно и
только одно возможное значение, наперед не известное и зависящее от
случайных причин, которые заранее не могут быть учтены.Примеры случайных величин:
1) число родившихся детей в течение суток в г. Ярославле;
2) количество бракованных изделий в данной партии;
3) число произведенных выстрелов до первого попадания;
4) дальность полета артиллерийского снаряда;
5) расход электроэнергии на предприятии за месяц.
Понятие случайной величины.
Слайд 6Понятие случайной величины тесно связано с понятием случайного события. Здесь
также первичным служит испытание, но результат теперь характеризуется не альтернативным
исходом (появляется или нет событие), а некоторым числом (например, число k появлений события в n повторных независимых испытаниях; число очков, выбиваемых стрелком).Связь со случайным событием заключается в том, что принятие ею некоторого числового значения есть случайное событие, характеризуемое вероятностью pi.
Понятие случайной величины
Слайд 7Примеры случайных величин:
X – число попаданий при 10-ти выстрелах по
цели.
X – число родившихся мальчиков среди 100 новорожденных.
Интервал
времени между моментами прихода автобусов к остановке в пределах от нуля до пяти минут. Понятие случайной величины
В примерах 1) и 2) случайные величины могут принимать конечное число значений – такие величины называются дискретными, а в примере 3) – целый промежуток, т.е. бесконечное и несчетное число значений - такие величины называются непрерывными.
Значения X: 0,1, 2, 3, …, 10.
Значения: 0,1, 2, …,99, 100.
Значения: [ 0;5 ].
Слайд 8Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения
с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть
конечным или бесконечным, но счетным. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Число возможных значений непрерывной случайной величины бесконечно.
Понятие случайной величины
Слайд 9Случайные величины будем обозначать прописными буквами латинского алфавита X, Y,
Z,..., а их значения — соответствующими строчными буквами хi, уi,
zi,... .Наиболее полным, исчерпывающим описанием случайной величины является ее закон распределения.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Про случайную величину говорят, что она «распределена» по данному закону распределения или «подчинена» этому закону распределения.
Закон распределения
Слайд 10Равномерный закон распределения
Закон распределения
Нормальный закон распределения
Пример распределения дискретной случайной
величины
Примеры распределения непрерывной случайной величины
Слайд 12 Для дискретной случайной величины закон распределения может быть задан
в виде таблицы, аналитически (в виде формулы) и графически.
В
виде таблицы (ряд распределения).Ряд распределения -таблица (матрица), в первой строке которой перечислены в порядке возрастания все возможные значения случайной величины, а во второй - соответствующие им вероятности, т.е.
Закон распределения
Слайд 13События Х=х1, Х=х2,..., Х=хn состоящие в том, что в результате
испытания случайная величина X примет соответственно значения х1, х2,..., хn,
являются несовместными и единственно возможными (т.к. в таблице перечислены все возможные значения случайной величины), т.е. образуют полную группу.Следовательно, сумма их вероятностей равна 1. Таким образом, для любой дискретной случайной величины
Закон распределения
Слайд 14Закон распределения
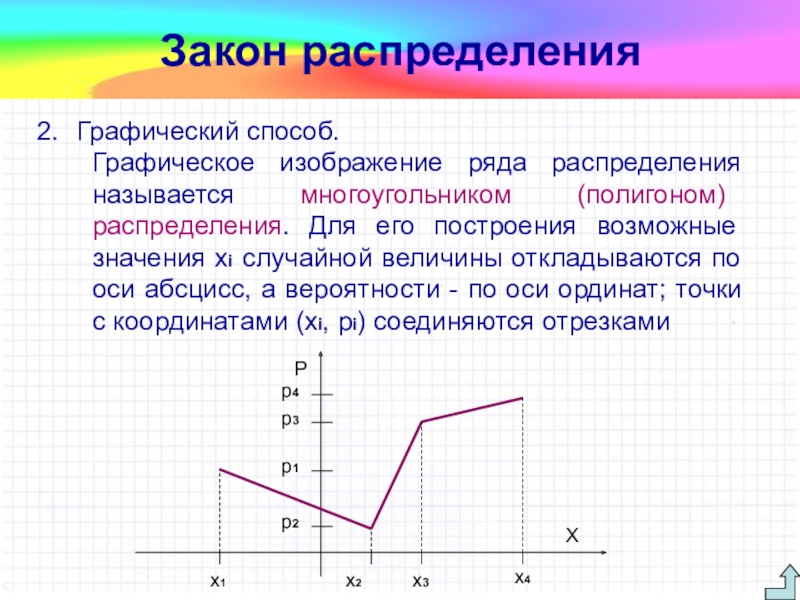
Графический способ.
Графическое изображение ряда распределения называется многоугольником (полигоном) распределения.
Для его построения возможные значения xi случайной величины откладываются по
оси абсцисс, а вероятности - по оси ординат; точки с координатами (xi, pi) соединяются отрезкамиСлайд 15Аналитический способ.
Аналитическим выражением закона распределения может быть, например формула Бернулли
(в случае биноминального распределения), формула Пуассона (в случае распределения Пуассона),
формула геометрической прогрессии (в случае геометрического распределения) и т.д.Закон распределения
Слайд 16Пример. Вероятность попадания стрелком в цель равна 0,8. Найти закон
распределения ДСВ Х - числа промахов при 5 выстрелах.
Закон
распределенияРешение.
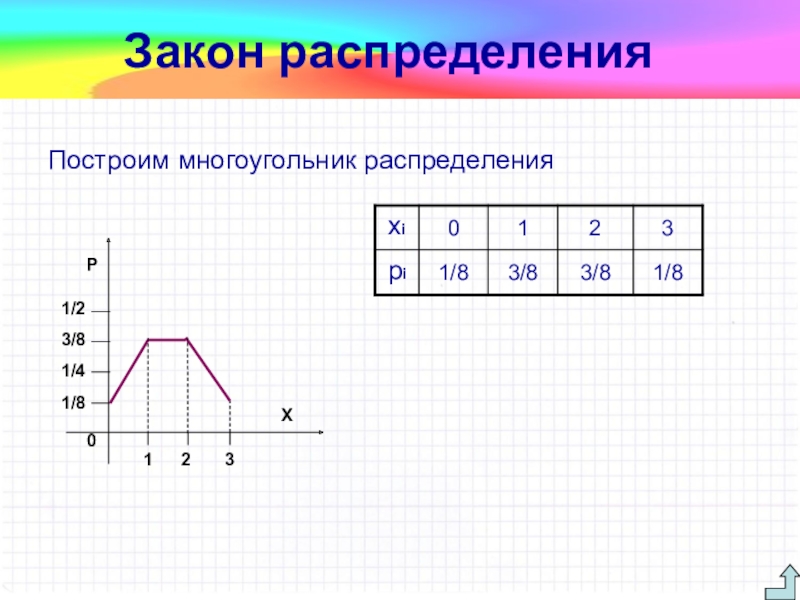
Слайд 17Пример. Найти ряд распределения случайной величины, являющейся частотой выпадения “орла”
при трех бросаниях монеты. Построить полигон распределения вероятностей.
Решение.
Закон распределения
Проверка:
1/8+3/8+3/8+1/8 = 1Х - частота выпадения “орла” при трех бросаниях монеты.
Возможные значения частоты X выпадения “орла” следующие:
0,1,2,3.
Соответствующие вероятности нетрудно подсчитать по формуле классической вероятности. Число всех возможных случаев равно 8: (ооо), (оор), (оро), (орр), (роо), (рор), (рро), (ррр).
P(X=0)= 1/8, P(X=1)= 3/8, P(X=2)= 3/8, P(X=3)= 1/8
Таким образом, запишем ряд распределения
Слайд 20Две случайные величины называются независимыми, если закон распределения одной из
них не меняется от того, какие возможные значения приняла другая
величина.В противном случае случайные величины называются зависимыми.
Например, если имеются билеты двух различных денежных лотерей, то случайные величины X и Y, выражающие соответственно выигрыш по каждому билету (в денежных единицах), будут независимыми.
Если же случайные величины X и Y выражают выигрыш по билетам одной денежной лотереи, то в этом случае X и Y являются зависимыми, ибо любой выигрыш по одному билету (X = xi) приводит к изменению вероятностей выигрыша по другому билету (Y), т.е. к изменению закона распределения Y.
Операции над ДСВ
Слайд 21Пусть дана случайная величина Х.
Произведением k∙Х случайной величины X на
постоянную величину k называется случайная величина, которая принимает значения k∙xi
с теми же вероятностями pi (i = 1, 2, ..., n).Операции над ДСВ
Слайд 22Пример. Пусть дана случайная величина Х:
Найти закон распределения случайной величины
Y = 3Х
Решение. По определению
Операции над ДСВ
Слайд 23m-й степенью случайной величины X, т.е. , называется
случайная величина, которая принимает значения с теми
же вероятностями pi (i= 1, 2, ..., n).Вернемся к предыдущему примеру. Закон распределения ДСВ
будет такой:
Операции над ДСВ
Слайд 24Суммой случайных величин X и Y называется случайная величина X+Y,
возможные значения которой равны суммам каждого возможного значения X с
каждым возможным значением Y; вероятности возможных значений X+Y для независимых величин X и Y равны произведениям вероятностей слагаемых; для зависимых величин — произведениям вероятности одного слагаемого на условную вероятность второго.Операции над ДСВ
Слайд 26Произведением независимых случайных величин X и Y называется случайная величина
XY, возможные значения которой равны произведениям каждого возможного значения X
на каждое возможное значение Y; вероятности возможных значений произведения XY равны произведениям вероятностей возможных значений сомножителей.Операции над ДСВ
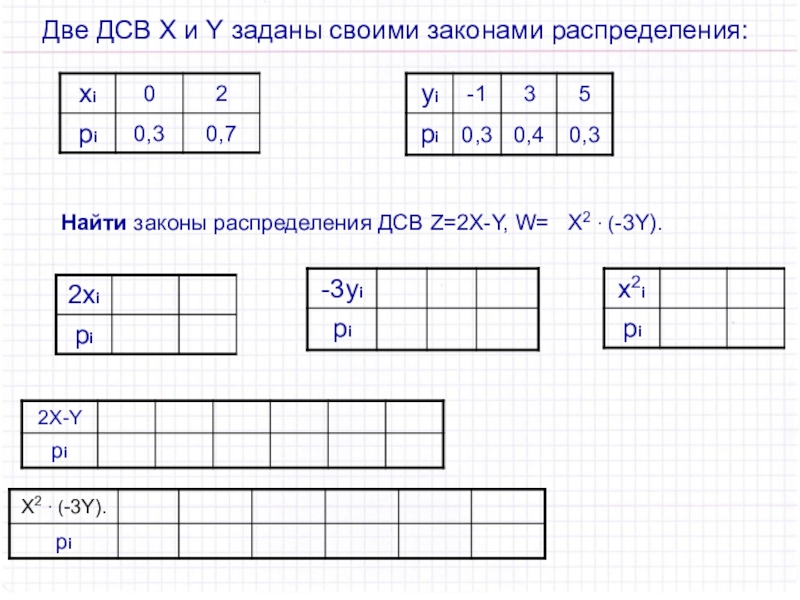
Слайд 28Две ДСВ X и Y заданы своими законами распределения:
Найти законы
распределения ДСВ Z=2X-Y, W= Х2 ∙ (-3Y).
Слайд 29Операции над ДСВ
Пример. Две ДСВ X и Y заданы своими
законами распределения:
Найти законы распределения ДСВ Z=X+2Y, W= ∙
(-3X).Решение. Запишем закон распределения для 2Y, , -3X.
2Y:
-3X:
Проверка: 0,12+0,08+0,06+0,04+0,42+0,28=1
Слайд 32Задача. Известны законы распределения случайных величин Х и Y —
числа очков, выбиваемых 1-м и 2-м стрелками.
Числовые характеристики ДСВ
X:
Y:
Необходимо выяснить, какой из двух стрелков стреляет лучше.
Решение. Очевидно, что из двух стрелков лучше стреляет тот, кто в
среднем выбивает большее количество очков.
Таким средним значением случайной величины является ее математическое ожидание.
Слайд 33Математическим ожиданием, или средним значением, М(Х) дискретной случайной величины X
называется сумма произведений всех ее значений на соответствующие им вероятности:
Математическое ожидание ДСВ
Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Слайд 34Решение. По определению математического ожидания:
М(Х)=0∙0,15 + 1∙0,11+ 2∙0,04 +
3∙0,05 + 4∙0,04 + 5∙0,1 + 6∙0,1 + 7∙0,04 +
8∙0,05 + 9∙0,12 + 10∙0,2 = 5,36M(Y)=0∙0,01 + 1∙0,03 + 2∙0,05 + 3∙0,09 + 4∙0,11 + 5∙0,24 + 6∙0,21 + 7∙0,1 + 9∙0,04 + 10∙0,02 = 5,36
Ответ: Среднее число выбиваемых очков у двух стрелков одинаковое.
Пример. Вычислить М(Х) и M(Y) в предыдущей задаче о стрелках.
Х:
Y:
Математическое ожидание ДСВ
Слайд 35Решение. Возможные значения случайной величины X - чистого выигрыша на
один билет - равны:
0 - 7 = -7 ден.
ед. (если билет не выиграл), 200 - 7 = 193, 250 - 7 = 243, 5000 - 7 = 4993 ден. ед. (если на билет выпал выигрыш соответственно видеомагнитофона, телевизора или автомобиля). Математическое ожидание ДСВ
Пример. В лотерее разыгрываются:
1 автомобиль стоимостью 5000 ден. ед.,
4 телевизора стоимостью 250 ден. ед.,
5 видеомагнитофонов стоимостью 200 ден. ед.
Всего продается 1000 билетов по 7 ден. ед. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим один билет. Найти математическое ожидание.
Учитывая, что из 1000 билетов число невыигравших составляет 990, а указанных выигрышей соответственно 5, 4 и 1, и используя классическое определение вероятности, получим:
Р(Х=-7) = 990/1000 = 0,990; P(X=193) = 5/1000 = 0,005;
Р(Х=243) = 4/1000 = 0,004; Р(X=4993) = 1/1000 = 0,001.
Слайд 36т.е. ряд распределения X:
Математическое ожидание ДСВ
Найдем математическое ожидание:
М(Х) = (-7)∙0,990
+ 193∙0,005 + 243∙0,004 + 4993∙0,001 = 0,
т.е. средний
выигрыш равен нулю.Р(Х=-7) = 990/1000 = 0,990; P(X=193) = 5/1000 = 0,005;
Р(Х=243) = 4/1000 = 0,004; Р(X=4993) = 1/1000 = 0,001.
Слайд 37Свойства математического ожидания:
Математическое ожидание постоянной величины равно самой постоянной: M(С)
= С.
Постоянный множитель можно выносить за знак математического ожидания,
т.е. М(kХ) = kМ(Х). Математическое ожидание алгебраической суммы конечного числа случайных величин равно сумме их математических ожиданий, т.е. М(Х± Y) = М(Х) ± M(Y).
Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий M(XY) = M(X)∙M(Y).
Математическое ожидание
Слайд 38Пример. Найти математическое ожидание случайной величины Z= 8Х- 5XY+ 7,
если известно, что М(Х) = 3, M(Y)= 2.
Решение. Используя
свойства 1, 2, 3, 4 математического ожидания, найдем M(Z)= M(8Х - 5XY+ 7)= M(8X) – M(5XY) + M(7)= 8M(X) – 5M(X)∙M(Y) +7 = 8∙3 - 5∙3∙2 +7 = 24 – 30 + 7 = 1
Ответ: математическое ожидание случайной величины Z равно 1.
Математическое ожидание
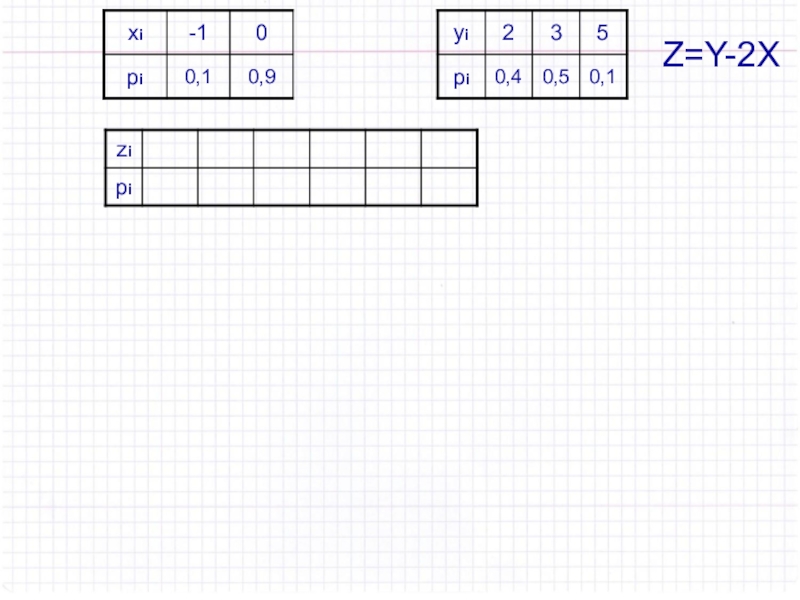
Слайд 39Пример. Даны распределения случайных величин Х и Y:
Математическое ожидание
Найти математическое
ожидание M(Z) случайной величины Z=Y-2X двумя способами:
исходя из закона распределения
Z;используя свойства математического ожидания.
Убедиться в том, что в условиях данной задачи эти свойства матожидания независимых случайных величин выполняются.
Слайд 41Пример. В результате обработки данных многолетних наблюдений получены распределения случайных
величин Х и Y – числа хозяйств в каждом из
двух районов области, в которых урожайность яровых зерновых культур может превысить 35 ц/га.Для первого района: Для второго района:
Математическое ожидание
Найти математическое ожидание M(Z) случайной величины Z=X+Y двумя способами:
исходя из закона распределения Z;
используя свойства математического ожидания.
Убедиться в том, что в условиях данной задачи эти свойства матожидания независимых случайных величин выполняются.
Слайд 42Математическое ожидание
Решение.
1) Найдем закон распределения ДСВ Z=X+Y:
Z:
Z:
M(Z) = 1∙0.02
+ 2∙0.2 +3∙0.54 + 4∙0.24 = 3
2) Вычислим матожидание ДСВ
Z=X+Y, используя свойства.Найдем M(X) и M(Y):
M(X) = 1∙0.1 + 2∙0.6 + 3∙0.3= 2.2
M(Y) = 0∙0.2 + 1∙0.8 = 0.8
M(Z) = M(X+Y) = M(X) + M(Y) = 2.2 + 0.8 =3.
Сравнив значение M(Z), полученное в пункте 1), с соответствующим ему значением, полученное в пункте 2), убеждаемся в том, что матожидания Z, найденные двумя различными способами, совпадают.
X:
Y:
Слайд 43Рассмотрим две ДСВ:
X:
Y:
Дисперсия
Найдем математические ожидания этих величин:
M(X) = -0,01∙0,5 +
0,01∙0,5 = -0,005 + 0,005 = 0.
M(Y) = -150∙0,4 +
100∙0,6 = -60 + 60 = 0Математические ожидания обеих величин одинаковы, а возможные значения различны, причем X имеет возможные значения, близкие к математическому ожиданию, а У - далекие от своего математического ожидания.
Для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
Слайд 44Пусть X - случайная величина и М (X) - ее
математическое ожидание. Рассмотрим в качестве новой случайной величины разность X
- М(Х).Отклонением называют разность между случайной величиной и ее математическим ожиданием.
Пусть закон распределения X известен:
Дисперсия
Найдем закон распределения отклонения:
X - М(Х):
Слайд 45Пример. Задан закон распределения дискретной случайной величины X.
Найти закон
распределения её отклонения.
Решение. Вычислим математическое ожидание Х:
М(Х) = 2 ∙0,2
+ 4 ∙0,8 = 0,4 + 3,2 = 3,6.Найдем возможные значения отклонения: х1 – М(Х) = 2 – 3,6 = -1,6;
х2 – М(Х) = 4 – 3,6 = 0,4.
Следовательно закон распределения отклонения будет следующим
Х – М(Х):
Дисперсия
Х:
Слайд 46
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата
отклонения случайной величины от ее математического ожидания: D(X)
= M (X – M(X))².Пусть случайная величина задана законом распределения:
Х:
Найдем закон распределения её отклонения от матожидания:
Х – M(X):
Найдем закон распределения квадрата её отклонения от матожидания:
(Х – M(X))2:
Дисперсия
Слайд 47Пример. Вычислим дисперсию для ДСВ Х из предыдущего примера.
Х:
Дисперсия
Х
– М(Х):
(Х – М(Х))2 :
D(Х) = M(X - M(X))2 =
2,56∙0,2 +0,16∙0,8 = 0.64Ответ: D(Х) = 0,64
М(Х) = 2 ∙0,2 + 4 ∙0,8 = 0,4 + 3,2 = 3,6.
Слайд 49Формула для вычисления дисперсии.
Дисперсия равна разности между математическим ожиданием квадрата
случайной величины X и квадратом ее математического ожидания:
D(X)
= M (X2)—[М (X)]2. Пример 1. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
Дисперсия
Решение. Найдем математическое ожидание М (X):
М (Х) = 2 ∙ 0,1+3 ∙ 0,6 + 5 ∙ 0,3 = 3,5.
Найдем математические ожидания М (Х2):
М(Х2) = 4 ∙ 0,1 +9 ∙ 0,6 + 25 ∙ 0,3= 13,3.
Искомая дисперсия: D(X)= M (X2)—[М (Х)]2 = 13,3 – (3,5)2 = 1,05.
Х:
Х2:
Слайд 50Средним квадратическим отклонением случайной величины X называют квадратный корень из
дисперсии:
Cреднее квадратическое отклонение
Пример. Найти среднее квадратическое отклонение ДСВ Х,
заданной законом распределения. Х:
Х2:
Вычислим М(Х) и М(Х2):
М(Х) = 1∙0,2 + 3∙0,6 + 6∙0,2 = 3,2.
М(Х2) = 1∙0,2 + 9∙0,6 + 36∙0,2 = 12,8.
D(X) = М(Х2) – [М(Х)]2 = 12.8 – 3.22 = 12.8 – 10,24 = 2,56.
Слайд 51Свойства дисперсии:
Дисперсия постоянной величины С равна нулю:
D (С)
= 0.
Постоянный множитель можно выносить за знак дисперсии, возводя
его в квадрат: D(kX) = k2D(X).
Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D(X + Y) = D(X) + D(Y).
Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D(X - Y) = D(X) + D(Y).
Дисперсия
Слайд 52Пример. Даны две ДСВ X и Y:
X:
Y:
Найти матожидание и
дисперсию ДСВ Z =X-2Y двумя способами:
Исходя из закона распределения Z;
Используя
свойства матожидания и дисперсии.Решение. 1)Составим закон распределения Z:
Слайд 53Пример. Даны две ДСВ X и Y:
X:
Y:
Найти матожидание и
дисперсию ДСВ Z =Y-X двумя способами:
Исходя из закона распределения Z;
Используя
свойства матожидания и дисперсии.Решение. 1)Составим закон распределения Z:
Z:
Z:
Числовые характеристики ДСВ
M(Z)= -5∙0,14 + -3∙0,34 + -1∙0,28 + 1∙0,28 + 3∙0,12 = -1,2.
M(Z2)= 25∙0,14 + 9∙0,34 + 1∙0,28 + 1∙0,28 + 9∙0,12 = 8,04.
D(Z)= M(Z2) - (M(Z))2 =8,04 – (-1,2)2= 6,6.
Слайд 542) Z =Y-X. Найдем M(Z) и D(Z), используя свойства этих
числовых характеристик.
X:
Числовые характеристики ДСВ
Y:
Сравнив значение M(Z) и D(Z), полученные в
пункте 1), с соответствующими им значениями, полученными в пункте 2), убеждаемся в том, что числовые характеристики Z, найденные двумя различными способами, совпадают.M(X)=1∙0,3 + 3∙0,7= 2,4; M(X2)=1∙0,3 + 9∙0,7 =6,6;
D(X)= M(Х2)- (M(Х))2 = 6,6 – 2,42 = 0,84.
M(Y)=-2∙0,2 + 0∙0,4 + 4∙0,4= 1.2; M(Y2)=4∙0,2 + 0∙0,4 + 16∙0,4 =7,2;
D(Y)= M(Y2)- (M(Y))2 = 7,2 – 1,22 = 5,76.
M(Z) =M(Y-X) = M(Y)-M(X) = 1,2 – 2,4 = -1,2.
D(Z) = D(Y-X) = D(Y) + D(X) = 5,76 + 0,84 = 6,6.