Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей и математическая статистика
Содержание
- 1. Теория вероятностей и математическая статистика
- 2. http://study.sfu-kras.ruЭлектронные курсы СФУИнститут Экономики, управления и природопользования
- 3. Электронный курс
- 4. ПособияКрупкина, Т. В. Теория вероятностей и математическая
- 5. ЭЛЕКТРОННЫЙ КАТАЛОГ НАУЧНОЙ БИБЛИОТЕКИ СФУ: ЛИТЕРАТУРА ПО ЕСТЕСТВЕННЫМ И ГУМАНИТАРНЫМ НАУКАМhttp://liber.lib.sfu-kras.ru/phpopac/elcat.phpСделать поиск по фамилии Крупкина.
- 6. Слайд 6
- 7. Слайд 7
- 8. Эконометрика : электронный учеб.-метод. комплекс : [авт.
- 9. Рекомендуемая литератураБулдык Г.М. Теория вероятностей и математическая
- 10. Полезные ссылкиhttp://www.exponenta.ru/educat/class/courses/tv/theme0/5.asphttp://teoriaver.narod.ru/ http://www.nsu.ru/mmf/tvims/chernova/tv/lec/lec.html
- 11. Промежуточный контроль 75%Контрольная «Теория вероятностей» :
- 12. Введение в теорию вероятностей Предметом теории вероятностей
- 13. Введение в теорию вероятностей Первая задача шевалье
- 14. Введение в теорию вероятностейВ настоящее время теория
- 15. Введение в теорию вероятностейВопрос о применимости вероятностных
- 16. Статистическое определение вероятности Пусть рассматриваемый опыт можно
- 17. Статистическое определение вероятности Практика показывает, что для
- 18. Классическое определение вероятностиРассмотрим некоторый опыт с конечным
- 19. Пусть n – число всех исходов, n(A)
- 20. Пример В урне 2 белых и 5 черных
- 21. Формулы комбинаторикиЧисло перестановок Число перестановок из n элементов равно
- 22. Число перестановокПример 1 Сколько существует способов расставить на полке 10 различных книг? Ответ: 10!
- 23. Число перестановокПример 2 Сколько существует различных способов распределить 5 задач по пяти вариантам? Ответ: 5!
- 24. Формулы комбинаторикиВыбор с возвращением Пусть имеется r групп,
- 25. Выбор с возвращением В частности, если
- 26. Выбор с возвращениемПример 3 Сколько существует различных способов из цифр 1, 2, …9 составить двузначное число?Ответ: 92.
- 27. Выбор без возвращения Число размещений С помощью
- 28. Число размещенийПример 4Сколько существует способов составить из
- 29. Выбор без возвращенияЧисло сочетаний С помощью этой формулы
- 30. Число сочетаний
- 31. Число сочетанийПример 5 Сколько существует способов составить из
- 32. Число способов, которыми можно разбить n различных
- 33. Число разбиений на группыПример 6 Сколько существует различных
- 34. Пример 7 В урне 2 белых и 5
- 35. Пример 8 В урне a белых и
- 36. Пример 9 Из пяти букв разрезной азбуки составлено
- 37. Пример 10 Из букв разрезной азбуки составлено слово
- 38. Элементарные исходыПространством элементарных исходов Ω называется множество,
- 39. Событиями мы будем называть некоторые наборы элементарных
- 40. ПримерБросаем один раз игральную кость. В этом
- 41. Дискретное пространствоПространство элементарных исходов назовём дискретным, если
- 42. События в дискретном пространстве ΩОпределение Произвольные подмножества
- 43. В пространстве элементарных событий Ω = {
- 44. Замечание Пустое множество и все множество
- 45. Элементарные событияДостоверное событие наступает при любом
- 46. ПримерБросаем один раз игральную кость. Выпадение более
- 47. ОпределенияСобытия называются равными (A1 = A2), если
- 48. ПримерБросаем один раз игральную кость. Событие A
- 49. Комбинации событийРассмотрим комбинации событий, такие, как сумма,
- 50. Суммой или объединением событий A1 и A2
- 51. ПримерБросаем один раз игральную кость. Событие A
- 52. Произведением или пересечением событий A1 и A2
- 53. ПримерВ условиях предыдущего примера:Событие A - выпадение
- 54. Разностью событий A1 и A2 называют событие
- 55. ПримерВ условиях предыдущего примера:Событие A - выпадение
- 56. Противоположным событием к событию A называют событие
- 57. ПримерВ условиях предыдущего примера:Событие A - выпадение
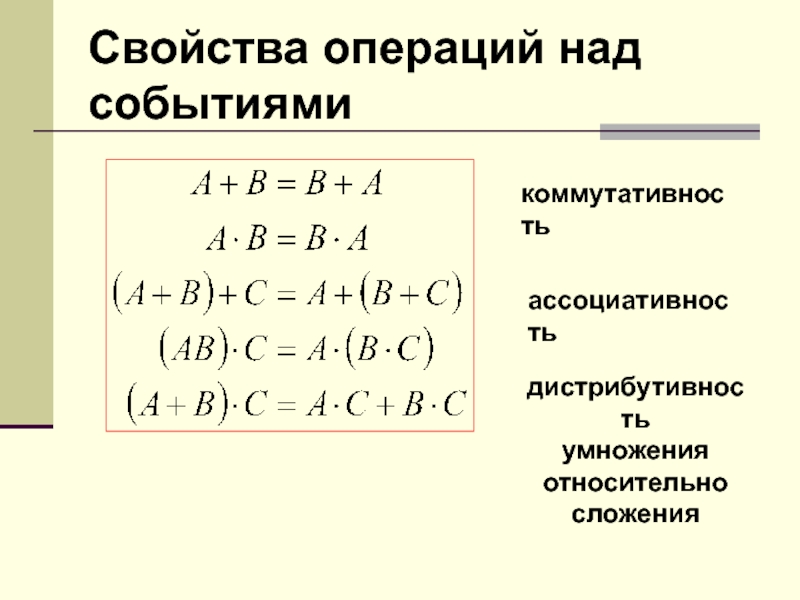
- 58. Свойства операций над событиямикоммутативностьассоциативностьдистрибутивность умножения относительно сложения
- 59. Слайд 59
- 60. Вероятность в классическом пространстве Классическая вероятность может
- 61. Описать пространство Ω элементарных исходов в случае
- 62. Решение (продолжение)Множество элементарных исходов можно задать перечислением:
- 63. Найти вероятность события A={суммарное число выпавших очков равно 6}.
- 64. По-другому этот результат можно получить, если сложить вероятности элементарных исходов
- 65. Замечание.Вероятность, вычисленная в этом примере, была найдена
- 66. Проблема!Но множество исходов не обязательно конечно или
- 67. Аксиоматическое определение вероятностиОпределение Вероятность события есть числовая функция P(A), удовлетворяющая аксиомам:
- 68. Свойства вероятности
- 69. Проблема!Если несчетно, то не всякое подмножество
- 70. – алгебраОпределение F называется –алгеброй, если
- 71. Пример 1. {, }. 2. {, A, Ā, }, где A – некоторое подмножество .
- 72. Аксиоматика КолмогороваОпределение Вероятностным пространством называется тройка (,
- 73. Геометрическое вероятностное пространство Рассмотрим какую-нибудь область (на
- 74. Эксперимент состоит в случайном выборе точки из
- 75. Пример Точка наудачу бросается на отрезок [0;1]. Вероятность
- 76. Пример Вероятность точке попасть в точку {0,5} равна
- 77. Пример (Задача о встрече) Два лица X и
- 78. Решение Будем считать интервал с 14 до
- 79. Можно считать, что эксперимент сводится к бросанию
- 80. Задача Бюффона На плоскости начерчены параллельные прямые,
- 81. Решение Возможные положения иглы (отрезка) на плоскости полностью
- 82. Обозначим через x[0,a] расстояние от середины иглы
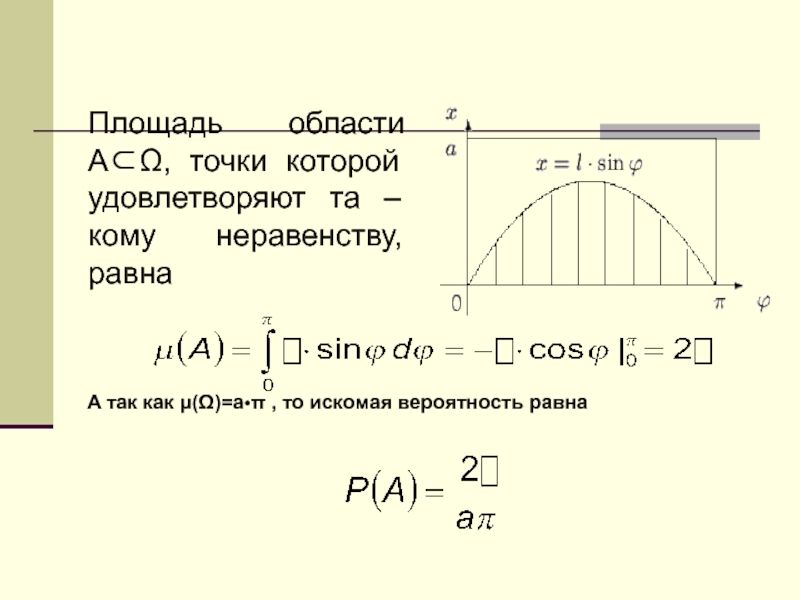
- 83. Площадь области A, точки которой удовлетворяют та
- 84. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2http://study.sfu-kras.ru
Электронные курсы СФУ
Институт Экономики, управления и природопользования
Теория вероятностей и
математическая статистика (лектор Т.В. Крупкина)
Слайд 4Пособия
Крупкина, Т. В. Теория вероятностей и математическая статистика (для
студентов экономического факультета): Учеб. пособие. /
Т. В. Крупкина, С.
В. Бабенышев, Е. С. Кирик.Красноярск: СФУ, 2008.
Крупкина, Т. В. Теория вероятностей и математическая статистика в примерах и задачах (для студентов экономического факультета): Учеб. пособие. / Т. В. Крупкина, А.И. Пыжев, С. В. Бабенышев, Е. С. Кирик.
Красноярск: СФУ, 2008
Слайд 5ЭЛЕКТРОННЫЙ КАТАЛОГ НАУЧНОЙ БИБЛИОТЕКИ СФУ:
ЛИТЕРАТУРА ПО ЕСТЕСТВЕННЫМ И ГУМАНИТАРНЫМ
НАУКАМ
http://liber.lib.sfu-kras.ru/phpopac/elcat.php
Сделать поиск по
фамилии Крупкина.
Слайд 8Эконометрика : электронный учеб.-метод. комплекс : [авт. ред.] : Теория
вероятностей и математическая статистика : учеб. Пособие
Эконометрика : электронный учеб.-метод.
комплекс : [авт. ред.] : Теория вероятностей и математическая статистика в примерах и задачах : учеб. пособиеСлайд 9Рекомендуемая литература
Булдык Г.М. Теория вероятностей и математическая статистика. Минск: Вышейш.
шк., 1989. 285 с.
Колемаев В. А., Калинина В. Н. Теория вероятностей и
математическая статистика. М.: ИНФРА-М, 2000.Крупкина Т.В., Гречкосеев А. К. Теория вероятностей и математическая статистика. Учеб. пособие. Краснояр.гос. ун –т; Красноярск, 1999. 216 с.
Слайд 10Полезные ссылки
http://www.exponenta.ru/educat/class/courses/tv/theme0/5.asp
http://teoriaver.narod.ru/
http://www.nsu.ru/mmf/tvims/chernova/tv/lec/lec.html
Слайд 11Промежуточный контроль
75%
Контрольная «Теория вероятностей» :
7
– 12 апреля (20%)
Контрольная «Математическая статистика» :
19 – 24 мая (20%)Домашние задания: (20%)
Лабораторная работа по мат. статистике, срок сдачи до 1 июня (15%)
Слайд 12Введение в теорию вероятностей
Предметом теории вероятностей является математический анализ
случайных явлений, то есть разработка и применение математического аппарата для
изучения явлений, имеющих случайную природу.Как самостоятельная наука, теория вероятностей была заложена в письмах Паскаля к Ферма в 1654г. В это время шевалье де Мере задал Паскалю два вопроса, касающиеся азартных игр.
Слайд 13Введение в теорию вероятностей
Первая задача шевалье де Мере :
сколько раз необходимо подбросить две игральные кости, чтобы вероятность выпадения
двух шестерок была больше половины?Вторая задача :
два игрока играют в азартную игру до n выигрышей. Как следует разделить между ними ставку, если игра прервана, когда первый игрок выиграл a, а второй b партий?
Слайд 14Введение в теорию вероятностей
В настоящее время теория вероятностей служит основой
для анализа тех явлений окружающего мира, которым свойственна «изменчивость», и
проявление которых не определяется однозначно условиями проводимых наблюдений.Слайд 15Введение в теорию вероятностей
Вопрос о применимости вероятностных и статистических методов
является непростым. Главным обстоятельством, которое определяет границы применимости теории вероятностей,
является наличие у изучаемых явлений свойства «статистической устойчивости».Слайд 16Статистическое определение вероятности
Пусть рассматриваемый опыт можно повторять многократно, и пусть
N – число всех повторений опыта, а N(А) – число
тех из них, в которых осуществлялось событие А. Отношение N(А)/N называется частотой события А в данной серии испытаний.Слайд 17Статистическое определение вероятности
Практика показывает, что для многих
событий частота при больших
п мало
меняется, колеблясь около некоторого
постоянного значения P*, которое можно
назвать статистической
вероятностью события А,Слайд 18Классическое определение вероятности
Рассмотрим некоторый опыт с конечным числом n всевозможных
взаимоисключающих друг друга исходов, которые являются равновозможными. Пусть А –
некоторое событие, связанное с этим исходом.Вероятность P(A) можно определить, как долю тех исходов, в результате которых это событие осуществляется.
Слайд 19Пусть n – число всех исходов, n(A) – число благоприятных
исходов, в результате которых осуществляется событие A.
Классическое определение вероятности
Слайд 20Пример
В урне 2 белых и 5 черных шаров. Из урны
вынимают наугад 1 шар. Найти вероятность, что вынут белый шар.
Решение:
Слайд 22Число перестановок
Пример 1
Сколько существует способов расставить на полке 10
различных книг?
Ответ: 10!
Слайд 23Число перестановок
Пример 2
Сколько существует различных способов распределить 5
задач по пяти вариантам?
Ответ: 5!
Слайд 24Формулы комбинаторики
Выбор с возвращением
Пусть имеется r групп, причем i –
ая группа содержит ni элементов, i = 1,
2, ..., r. Число способов, которыми можно выбрать r элементов по одному из каждой группы, равноСлайд 26Выбор с возвращением
Пример 3
Сколько существует различных способов из цифр 1,
2, …9 составить двузначное число?
Ответ: 92.
Слайд 27Выбор без возвращения
Число размещений
С помощью этой формулы можно подсчитать,
сколько существует различных способов выбрать и разместить по различным местам
k из n различных элементов.Формула числа размещений имеет вид:
Слайд 28Число размещений
Пример 4
Сколько существует способов составить из цифр 2, 3,
4, 5, 7, 8 двузначное число с различными цифрами?
Решение:
Слайд 29Выбор без возвращения
Число сочетаний
С помощью этой формулы можно подсчитать, сколько
существует различных способов выбора из n элементов k, не учитывая
порядок элементов в выбранной последовательности. Формула числа сочетаний имеет вид:Слайд 31Число сочетаний
Пример 5
Сколько существует способов составить из цифр 2, 3,
4, 5, 7, 8 сократимую дробь, выбирая два числа?
Решение:
Слайд 32 Число способов, которыми можно разбить n различных элементов на k
групп, содержащих соответственно n1, n2,…nk элементов, равно
Число разбиений
на группыСлайд 33Число разбиений на группы
Пример 6
Сколько существует различных способов разделить колоду
из 36 карт на 4 равные части?
Решение:
Слайд 34Пример 7
В урне 2 белых и 5 черных шаров. Из
урны вынимают наугад 2 шара. Найти вероятность, что оба шара
будут белыми.Решение:
Слайд 35Пример 8
В урне a белых и b черных шаров.
Из урны вынимают наугад 5 шаров. Найти вероятность, что два из них будут белыми, а три – черными.
Решение:
Слайд 36Пример 9
Из пяти букв разрезной азбуки составлено слово «КНИГА». Найти
вероятность того, что, перемешав буквы, и разложив их случайным образом,
получим то же самое слово.Ответ:
Слайд 37Пример 10
Из букв разрезной азбуки составлено слово «КОЛОБОК». Найти вероятность
того, что перемешав буквы, и разложив их случайным образом, получим
то же самое слово.Ответ:
Слайд 38Элементарные исходы
Пространством элементарных исходов Ω называется множество, содержащее все возможные
результаты данного случайного эксперимента, из которых в эксперименте происходит ровно
один. Элементы этого множества называют элементарными исходами и обозначают буквой ω.Слайд 39Событиями мы будем называть некоторые наборы элементарных исходов, то есть
подмножества множества Ω. Говорят, что в результате эксперимента произошло событие
A, если в эксперименте произошел один из элементарных исходов, входящих в множество.Слайд 40Пример
Бросаем один раз игральную кость. В этом опыте пространство элементарных
событий Ω = {1, 2, 3, 4, 5, 6}, где
элементарное событие i - выпадение i очков.Событие A - выпадение четного числа очков, A = {2, 4, 6},
событие B - выпадение числа очков, большего четырех, B = {5, 6}.
Слайд 41Дискретное пространство
Пространство элементарных исходов назовём дискретным, если оно конечно или
счётно.
Множество счётно, если существует взаимно-однозначное соответствие между этим множеством
и множеством всех натуральных чисел. Счётными множествами являются, например, множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество чётных чисел и т.д. Множество конечно, если оно состоит из конечного числа элементов.Слайд 42События в дискретном пространстве Ω
Определение
Произвольные подмножества дискретного пространства
элементарных исходов Ω называются событиями.
ВАЖНО:
Если Ω конечно или счётно, то
любое подмножество Ω может являться событием.Слайд 43В пространстве элементарных событий Ω = { 1, 2, 3,
4, 5, 6 } любой набор исходов ─ событие.
Например, {1,
3, 4, 5} или { 6 }. Слайд 44Замечание
Пустое множество и все множество тоже являются событиями.
Событие называется невозможным событием, событие – достоверным событием.
Слайд 45Элементарные события
Достоверное событие наступает при любом исходе.
Невозможное событие
не может произойти в результате эксперимента, оно не происходит никогда.
Случайное
событие может произойти или не произойти в результате эксперимента, оно происходит иногда.Слайд 46Пример
Бросаем один раз игральную кость. Выпадение более шести очков -
невозможное событие.
Выпадение не более шести очков - достоверное событие.
Выпадение от
трех до пяти очков - случайное событие.Слайд 47Определения
События называются равными (A1 = A2), если множества составляющих их
исходов совпадают:
События A1 и A2 называются несовместными, если их
множества элементарных исходов не пересекаются.Слайд 48Пример
Бросаем один раз игральную кость.
Событие A - выпадение четного
числа очков,
A = {2, 4, 6}.
Событие C - выпадение
нечетного числа очков, C = {1, 3, 5}.A и C несовместны.
Слайд 49Комбинации событий
Рассмотрим комбинации событий, такие, как
сумма, произведение, разность и
т.д.
Поскольку события – это множества исходов, будем использовать соответствующие определения
для множеств.Сумма событий соответствует объединению множеств, произведение событий соответствует пересечению множеств и т.д.
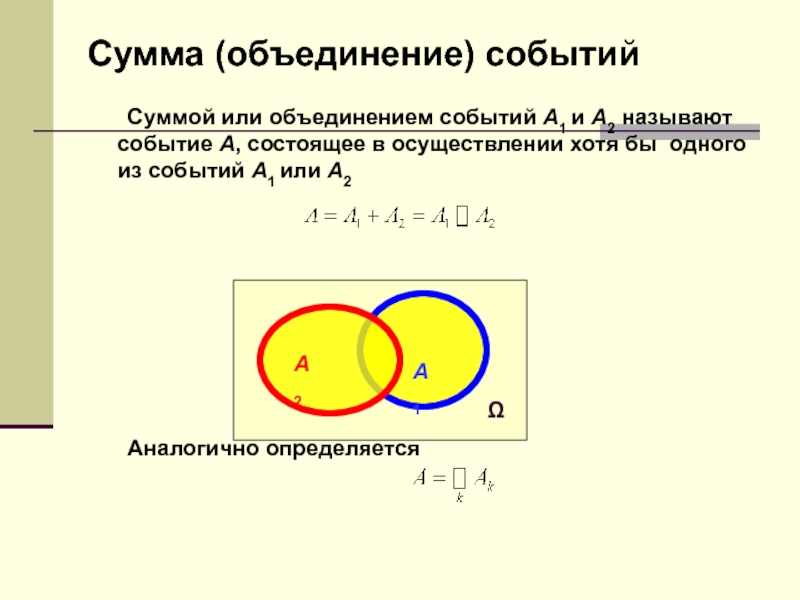
Слайд 50 Суммой или объединением событий A1 и A2 называют событие A,
состоящее в осуществлении хотя бы одного из событий A1 или
A2Аналогично определяется
Сумма (объединение) событий
A1
A2
Слайд 51Пример
Бросаем один раз игральную кость.
Событие A - выпадение четного
числа очков, A = {2, 4, 6}.
Событие B -
выпадение числа очков, большего четырех, B = {5, 6}. Событие A + B = {2, 4, 5, 6} состоит в том, что выпало либо четное число очков, либо число очков большее четырех, т.е. произошло либо событие A, либо событие B.
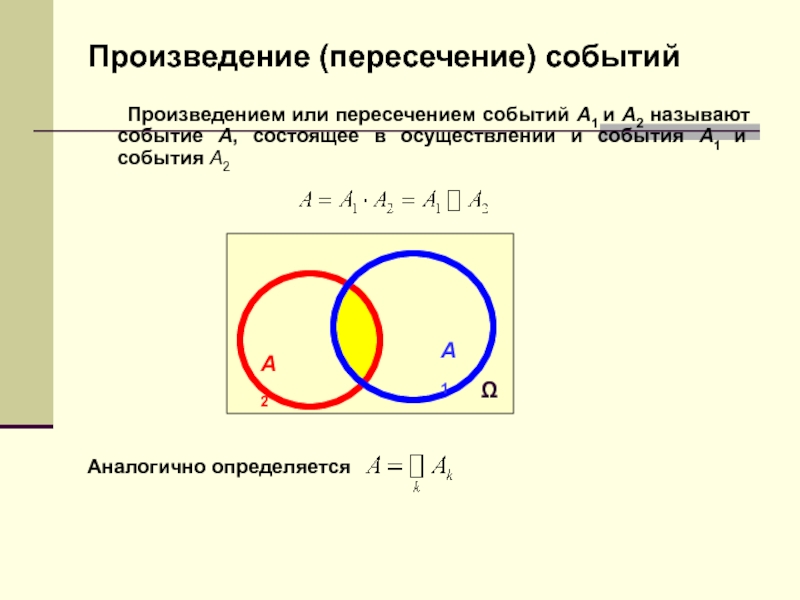
Слайд 52 Произведением или пересечением событий A1 и A2 называют событие A,
состоящее в осуществлении и события A1 и события A2
Аналогично
определяется A2
A1
Произведение (пересечение) событий
Слайд 53Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,
A = {2, 4, 6}.
Событие B - выпадение числа
очков, большего четырех, B = {5, 6}. Событие A B = {6} состоит в том, что выпало четное число очков, большее четырех, т.е. произошло и событие A, и событие B.
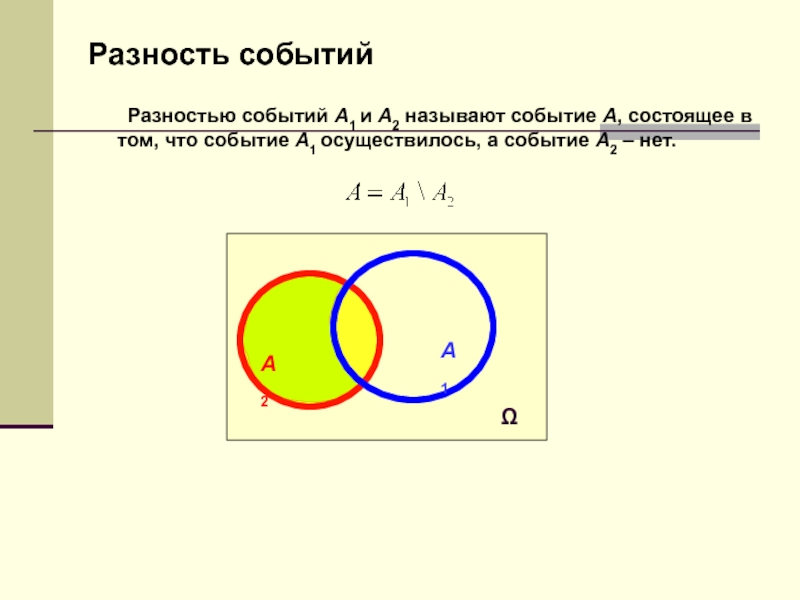
Слайд 54 Разностью событий A1 и A2 называют событие A, состоящее в
том, что событие A1 осуществилось, а событие A2 – нет.
A2
A1
Разность
событий
Слайд 55Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,
A = {2, 4, 6}.
Событие B - выпадение числа
очков, большего четырех, B = {5, 6}. Событие A\ B = {2, 4} состоит в том, что выпало четное число очков не большее четырех, т.е. произошло событие A, не произошло событие B.
Слайд 56
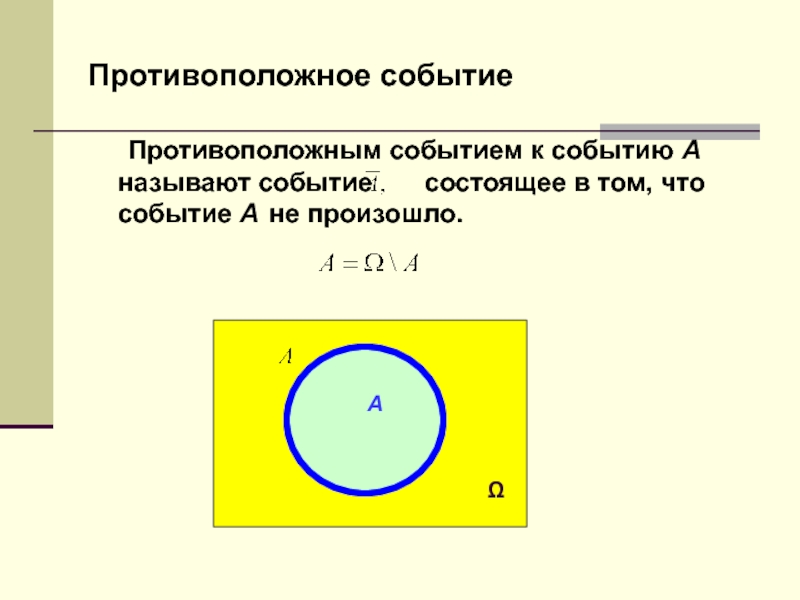
Противоположным событием к событию A называют событие
состоящее в том, что событие A не произошло.
A
Противоположное событие
Слайд 57Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,
A = {2, 4, 6}.
Событие =
{1, 3, 5} состоит в том, что выпало нечетное число очков, т.е. не произошло событие A. Слайд 58Свойства операций над событиями
коммутативность
ассоциативность
дистрибутивность
умножения
относительно
сложения
Слайд 60Вероятность в классическом пространстве
Классическая вероятность может быть записана как
где значок |A| обозначает число элементов в множестве A
(благоприятных исходов).Слайд 61 Описать пространство Ω элементарных исходов в случае бросания двух игральных
костей.
Решение
Элементарным исходом служит упорядоченная пара чисел ω
= (i, j), где i – число очков на первой кости, j – число очков на второй кости. Пример
Слайд 65Замечание.
Вероятность, вычисленная в этом примере, была найдена с помощью классического
определения вероятности. Но классическое определение можно применять только если исходы
равновозможны. А определение (*) можно применять и при неравновозможных исходах.Слайд 66Проблема!
Но множество исходов не обязательно конечно или счетно.
Пусть, например,
опыт состоит в выборе точки из отрезка [0, 1]. Исходом
является любая точка, а множество точек отрезка несчетно. Как ввести вероятность в этом случае?Слайд 67Аксиоматическое определение вероятности
Определение
Вероятность события есть числовая функция P(A), удовлетворяющая аксиомам:
Слайд 69Проблема!
Если несчетно, то не всякое подмножество является событием.
А
какие же подмножества являются событиями?
Ответ: только такие, которые входят в
так называемые –алгебры.Слайд 72Аксиоматика Колмогорова
Определение
Вероятностным пространством называется тройка (, F, P),
где
– пространство элементарных событий,
F – –алгебра подмножеств множества ,
P
– вероятностная мера, заданная на F.Слайд 73Геометрическое вероятностное пространство
Рассмотрим какую-нибудь область (на прямой, на плоскости,
в пространстве). Предположим, что «мера» конечна. Пусть случайный эксперимент состоит
в том, что мы наудачу бросаем в эту область точку.Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть A не зависит от формы или расположения A внутри , а зависит лишь от «меры» области.
Слайд 74 Эксперимент состоит в случайном выборе точки из ограниченного множества ;
F
– система подмножеств , у которых существует мера (длина, площадь,
объем и т.д. );где ||A|| – мера множества A.
Слайд 75Пример
Точка наудачу бросается на отрезок [0;1]. Вероятность точке попасть в
отрезок
[0,1; 0,5] равна 4/10 = 0,4. (Почему?)
А чему
равна вероятность точке попасть в полуоткрытый интервал [0,1; 0,5)?Тоже 4/10 = 0,4.
Слайд 76Пример
Вероятность точке попасть в точку {0,5} равна нулю, так как
мера множества, состоящего из одной точки («длина точки»), есть 0.
Вместе с тем попадание в точку {0,5} не является невозможным событием — это один из элементарных исходов эксперимента.
Слайд 77Пример (Задача о встрече)
Два лица X и Y условились встретиться
в определенном месте между двумя и тремя часами дня. Пришедший
первым ждет другого в течении 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?Слайд 78Решение
Будем считать интервал с 14 до 15 часов дня
отрезком [0,1] длиной 1 час. Пусть и –
моменты прихода X и Y (точки отрезка [0,1]).Все возможные результаты эксперимента – множество точек квадрата со стороной 1:
={(,): 0 1, 0 1} = [0,1]x[0,1]
Слайд 79 Можно считать, что эксперимент сводится к бросанию точки наудачу в
квадрат. При этом благоприятными исходами являются точки множества
A={(,): |
– | 1/6} То есть попадание в множество A наудачу брошенной в квадрат точки означает, что X и Y встретятся. Тогда вероятность встречи равна
Слайд 80Задача Бюффона
На плоскости начерчены параллельные прямые, находящиеся друг от
друга на расстоянии 2a. На плоскость наудачу брошена игла длины
2ℓ<2a. Какова вероятность того, что игла пересечет одну из прямых?Слайд 81Решение
Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины
иглы и углом поворота иглы относительно какого –либо направления. Причем
две эти переменные (положение центра и угол поворота) меняются независимо друг от друга.Слайд 82 Обозначим через x[0,a] расстояние от середины иглы до ближайшей прямой,
а через [0,] – угол между каким –то направлением прямых
и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника = [0,a]x[0,].
Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству: x ℓ•sin .




![Теория вероятностей и математическая статистика Эконометрика : электронный учеб.-метод. комплекс : [авт. ред.] : Теория вероятностей Эконометрика : электронный учеб.-метод. комплекс : [авт. ред.] : Теория вероятностей и математическая статистика : учеб. ПособиеЭконометрика](/img/tmb/4/355915/d9fca133d586d5befe6f0488df03adb6-800x.jpg)





























































![Теория вероятностей и математическая статистика Пример Точка наудачу бросается на отрезок [0;1]. Вероятность точке попасть в отрезок Пример Точка наудачу бросается на отрезок [0;1]. Вероятность точке попасть в отрезок [0,1; 0,5] равна 4/10 =](/img/tmb/4/355915/da4059d161e9fde907912055db5e6688-800x.jpg)


![Теория вероятностей и математическая статистика Решение Будем считать интервал с 14 до 15 часов дня отрезком Решение Будем считать интервал с 14 до 15 часов дня отрезком [0,1] длиной 1 час. Пусть ](/img/thumbs/a1454cc6c97e366034daf4e3cee267e0-800x.jpg)



![Теория вероятностей и математическая статистика Обозначим через x[0,a] расстояние от середины иглы до ближайшей прямой, а Обозначим через x[0,a] расстояние от середины иглы до ближайшей прямой, а через [0,] – угол между каким](/img/tmb/4/355915/502f84339c50b60e67eda41274bb2b82-800x.jpg)