Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятности и математическая статистика
Содержание
- 1. Теория вероятности и математическая статистика
- 2. Список литературыН. Ш. Кремер, Б. А. Путко,
- 3. Электронные материалы Y:\_Teachers\Guseva\ТВиМС
- 4. 1. Введение. Основные определения.
- 5. 1.1 Случайная величина. Закон распределения случайной величины.
- 6. В данном курсе мы учимся работать с
- 7. Закон распределения случайной величины содержит информацию о
- 8. В верхней строке таблицы указывают возможные значения
- 9. Если случайная величина может принимать непрерывный ряд
- 10. Вероятность того, что непрерывно распределенная случайная величина
- 11. Пример: Равномерное распределение случайной величины X ,
- 12. Чтобы перейти от непрерывного к дискретному распределению,
- 13. Совместное распределение случайных величин
- 14. Связь между случайными величинами можно описать, задав
- 15. Связь между случайными величинами не обязательно должна быть функциональной. Она может иметь статистический (стохастический) характер.
- 16. Функция случайной величины
- 17. Если каждому значению x случайной величины X
- 18. Вероятности , соответствующие значениям z и x,
- 19. Случайная величина Z может являться функцией нескольких
- 20. При построении функции нескольких случайных величин в
- 21. Для работы со случайными величинами удобно использовать
- 22. 1.2. Характеристики случайных величин
- 23. Математическое ожидание и дисперсия случайной величины.
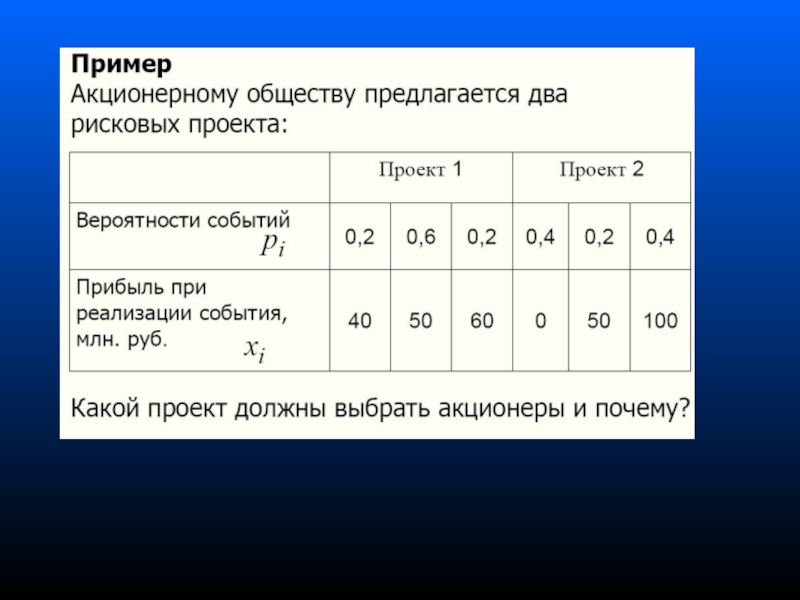
- 24. Задача. Вероятность
- 25. .
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Важной характеристикой степени связи между случайными величинами
- 30. Коэффициент корреляции представляет собой ковариацию нормированных случайных
- 31. 1.3. Связь между теорией вероятности и статистикой
- 32. Собирая статистические данные, мы получаем
- 33. В приведенной таблице величины аi задают границы
- 34. При обработке статистических данных на основе полученного
- 35. Из теоремы Бернулли (закона больших чисел) следует,
- 36. Из теоремы Чебышева следует, что наилучшей оценкой для математического ожидания случайной величины является ее среднее значение.
- 37. 2. Вычисление вероятности событий.
- 38. Испытание, исходы испытания
- 39. Полная группа событий
- 40. Вероятность, случайное событие
- 41. Случайная величина. С каждым (или несколькими сразу)
- 42. Закон распределения случайной величины содержит информацию
- 43. Пример: Закон распределения случайной величины X – числа очков, выпавших при броске игральной кости
- 44. Статистическое определение вероятности. Вероятность события оценивается на
- 45. Классическое определение вероятности.Вероятность события равна доле элементарных исходов испытания, при которых событие наступает.
- 46. При непосредственном
- 47. Размещения.
- 48. Перестановки
- 49. Сочетания:
- 50. Определение вероятности с помощью теории множеств.Вероятность события
- 51. Геометрическое определение
- 52. Рассмотрим испытание, состоящее
- 53. 3. Операции над событиями. Расчет вероятности произведения и суммы событий.
- 54. Известные вероятности
- 55. Произведение событий AB
- 56. Вероятность произведения событий
- 57. Вероятность произведения независимых событий (не влияющих друг на друга).
- 58. Невозможные и
- 59. Являются ли зависимыми события В и А ?
- 60. Сумма событий A+В
- 61. Вероятность суммы событий
- 62. Вероятность суммы несовместных событий. Несовместные события -
- 63. Противоположные события.
- 64. Противоположные события всегда образуют полную группу событий. Вероятность противоположного события
- 65. Слайд 65
- 66. Формула полной вероятности
- 67. Формула Байеса
- 68. 4. Биномиальный закон распределения дискретной случайной величины.
- 69. Формула Бернулли
- 70. Биномиальное распределение.
- 71. Математическое ожидание
- 72. Математическое ожидание
- 73. Слайд 73
- 74. .
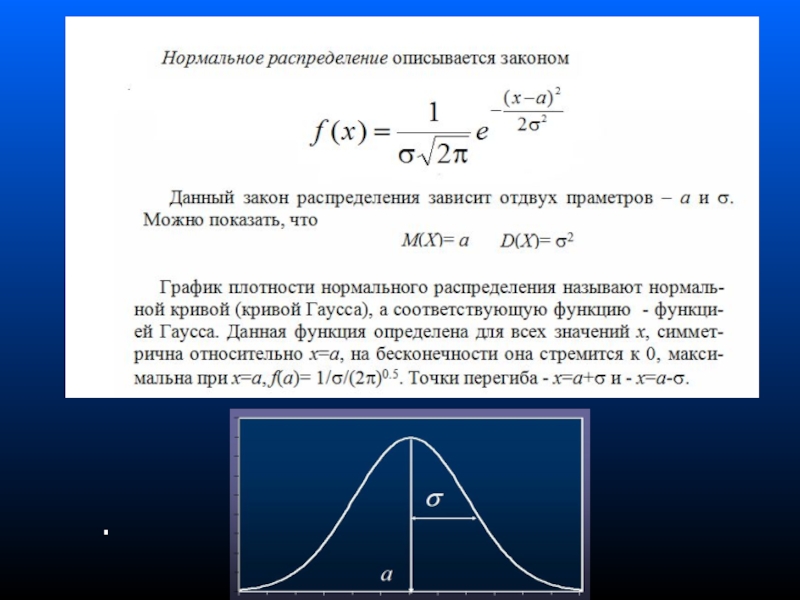
- 75. 5. Нормальное распределение непрерывной случайной величины.
- 76. .
- 77. Нормированное нормальное распределение
- 78. В случае, если
- 79. Правило «трех сигм».
- 80. Таблица вероятностей для отклонений в 1, 2 и 3 .
- 81. Центральная предельная
- 82. Скачать презентанцию
Список литературыН. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман. Математика для экономистов: от арифметики до эконометрики: учебно-справочное пособие для бакалавров. М.: Юрайт, 2012.Н.Ш. Кремер.Теория вероятности и математическая
Слайды и текст этой презентации
Слайд 1Теория вероятности и математическая статистика
Лектор -
Гусева Валентина Борисовна
доц. кафедры
информатики
Слайд 2Список литературы
Н. Ш. Кремер, Б. А. Путко, И. М. Тришин,
М. Н. Фридман. Математика для экономистов: от арифметики до эконометрики:
учебно-справочное пособие для бакалавров. М.: Юрайт, 2012.Н.Ш. Кремер.Теория вероятности и математическая статистика.
3. В.Е. Гмурман. Теория вероятностей и математическая статистика.
Слайд 6В данном курсе мы учимся работать с новым типом математических
величин – случайными величинами.
Случайная величина – это математическая величина,
принимающая одно из своих возможных значений случайным образом. Для обозначения случайных величин используют большие латинские буквы.
Пример: X – случайная величина, равная оценке студента на экзамене по статистике, или оценка.
Слайд 7Закон распределения случайной величины содержит информацию о том, какие значения
величина может принимать и насколько эти значения вероятны.
Если значения
представлены отдельными числами (случайная величина является дискретной) закон распределения задается в виде таблицы.Слайд 8 В верхней строке таблицы указывают возможные значения величины, в нижней
строке - вероятности реализации этих значений.
Когда случайная величина принимает одно
из возможных значений, этот факт можно рассматривать как наступление указанного события, обладающего определенной вероятностью.Под вероятностью события понимают количественную меру возможности наступления этого события.
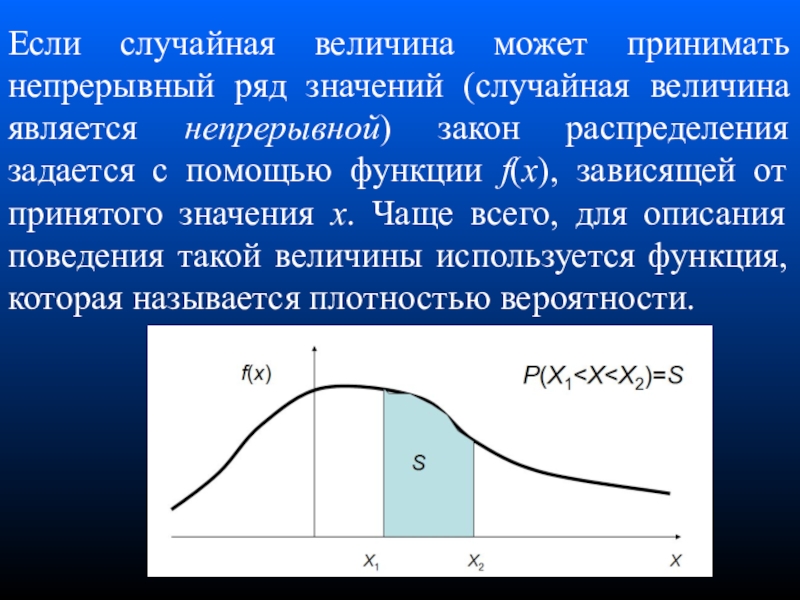
Слайд 9Если случайная величина может принимать непрерывный ряд значений (случайная величина
является непрерывной) закон распределения задается с помощью функции f(x), зависящей
от принятого значения x. Чаще всего, для описания поведения такой величины используется функция, которая называется плотностью вероятности.Слайд 10 Вероятность того, что непрерывно распределенная случайная величина примет конкретное значение,
всегда равна 0.
P(X=x0)=0. Для обозначения вероятности события используют букву
P, в скобках принято указывать событие, которому соответствует приведенная вероятность. Вероятность того, что непрерывная случайная величина примет значение, лежащее в заданном интервале, равна определенному интегралу от плотности вероятности на заданном интервале.
Слайд 11Пример: Равномерное распределение случайной величины X , принимающей значения в
интервале от a до b . Площадь закрашенной фигуры -
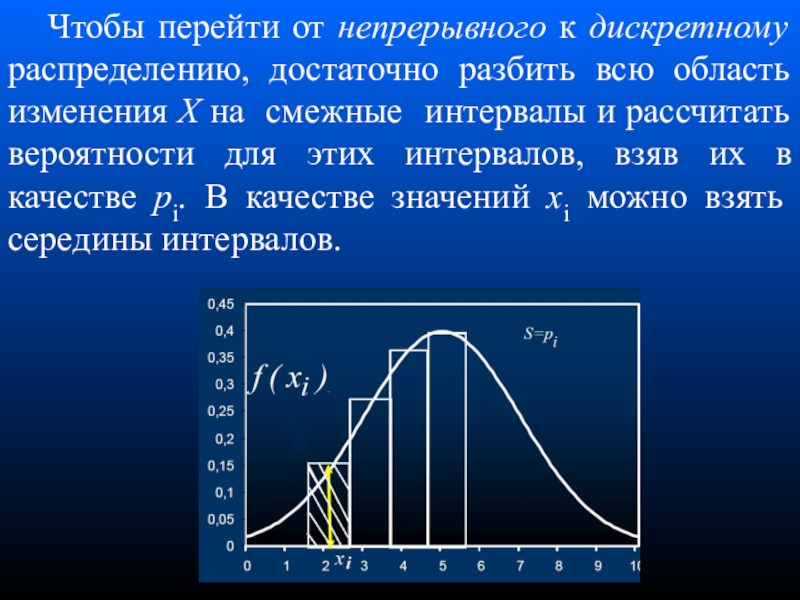
вероятность того, что значение случайной величины лежит в интервале от x1 до x2.Слайд 12 Чтобы перейти от непрерывного к дискретному распределению, достаточно разбить всю
область изменения X на смежные интервалы и рассчитать вероятности для
этих интервалов, взяв их в качестве pi. В качестве значений xi можно взять середины интервалов.Слайд 14Связь между случайными величинами можно описать, задав закон их совместного
распределения.
Для дискретных величин X и Y такой закон задается в
виде таблицы вероятностей, для непрерывных – в виде плотности вероятности совместного распределения f(x, y).
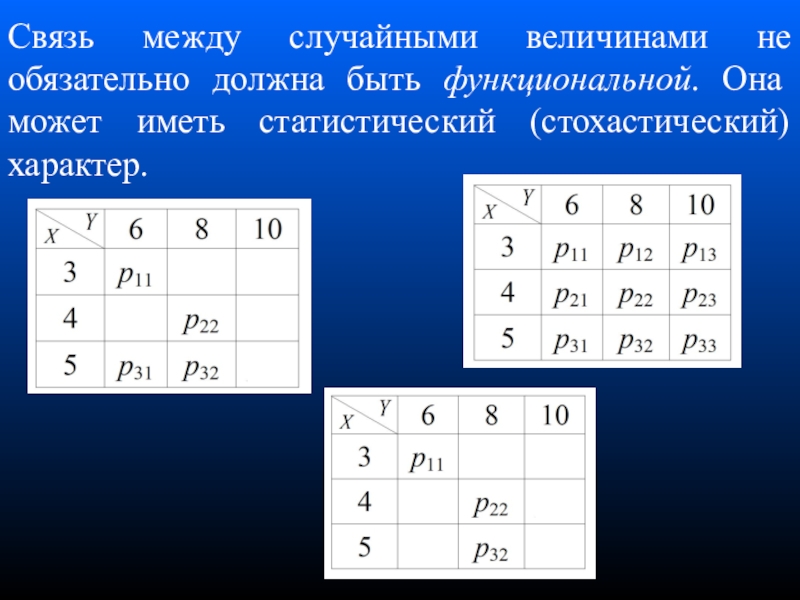
Слайд 15Связь между случайными величинами не обязательно должна быть функциональной. Она
может иметь статистический (стохастический) характер.
Слайд 17 Если каждому значению x случайной величины X поставить в соответствие
значение z=(x), мы построим новую случайную величину Z, которая является
функцией исходной случайной величины X и обозначается Z=(X).Слайд 18 Вероятности , соответствующие значениям z и x, могут не совпадать,
так как разным значениям x может соответствовать одно и то
же значение z.Слайд 19 Случайная величина Z может являться функцией нескольких случайных величин, если
ее значения вычисляются как функция возможных значений исходных величин.
Z = (X, Y), если каждой возможной паре значений x и y ставится в соответствие значение z=(x, y).Слайд 20 При построении функции нескольких случайных величин в качестве значений итоговой
величины в закон распределения включаются все возможные значения функции, полученные
из комбинации исходных случайных величин. Информация о вероятности этих значений берется из закона совместного распределения.Задача: Задав произвольно значения вероятностей pij, найдите закон распределения для случайной величины Z=X+Y, Z=XY, используя таблицы слайда 15
Слайд 21 Для работы со случайными величинами удобно использовать ряд параметров, которые
позволяют извлечь из законов распределения наиболее важную информацию. Это математическое
ожидание, дисперсия и коэффициент корреляции.Слайд 23Математическое ожидание и дисперсия случайной величины.
Математическое ожидание M(X) характеризует
некий средний уровень значений случайной величины X.
Дисперсия D(X) и среднеквадратичное
отклонение (X) (корень квадратный из дисперсии) – степень разброса отдельных значений величины X относительно этого уровня. Слайд 24 Задача.
Вероятность выиграть в лотерею
100 рублей (единственный приз) равна 0.001, вероятность ничего не выиграть
равна 0.999. Найдите математическое ожидание выигрыша, если билет стоит 1 рубль.Слайд 29Важной характеристикой степени связи между случайными величинами являются ковариация и
коэффициент корреляции.
Для дискретных случайных величин X и Y
Слайд 30Коэффициент корреляции представляет собой ковариацию нормированных случайных величин.
Здесь
-
нормированные случайные величины. Коэффициент корреляции может принимать значения в диапазоне
от -1 до 1. Если он равен 0, это может означать, что связь между величинами отсутствует, если он равен по модулю 1, то связь между величинами X и Y является функциональной.Слайд 32 Собирая статистические данные, мы получаем информацию о случайных
величинах (и их законах распределения) опытным путем. Полученные таким образом
статистические законы распределения (ряды распределения) также принято представлять в виде таблиц. В этих таблицах приводятся наблюдаемые значения случайной величины (в виде дискретных чисел или в виде интервалов, в зависимости от вида величины) и доля (процент) случаев, в которых наблюдалось данное значение.Случайные величины в статистике называют признаками, поскольку они характеризуют изучаемые свойства (признаки) объектов статистической совокупности.
Слайд 33В приведенной таблице величины аi задают границы интервалов в которых
лежат значения исследуемого признака (xi – середины интервалов), а wi
– доли объектов рассматриваемой статистической совокупности с величиной признака в указанном интервале.Слайд 34При обработке статистических данных на основе полученного эмпирического закона распределения
признака вычисляют такие параметры как среднее значение и дисперсия.
Слайд 35 Из теоремы Бернулли (закона больших чисел)
следует, что наилучшей статистической
оценкой для вероятности p события, которое может произойти в испытании,
является доля w=m/n успешных испытаний (тех, в которых это событие произошло) в серии из n испытаний.p w
при достаточно большом числе наблюдений n.
Слайд 36 Из теоремы Чебышева
следует, что наилучшей оценкой для математического ожидания
случайной величины является ее среднее значение.
Слайд 38Испытание, исходы испытания
Испытание
– совершение определенных действий, в результате которых возможно появление различных
случайных событий.Исход испытания – случайное событие, которое может произойти в результате проведения испытания. Множество исходов испытания – множество, состоящее из событий, являющихся исходами испытания.
Элементарный исход испытания – случайное событие, которое нельзя представить в виде комбинации более простых исходов испытания
Слайд 39Полная группа событий
Если случайные события
являются взаимоисключающими и в совокупности описывают все возможные исходы испытания,
они образуют полную группу событий.Пример:
Рассмотрим множество элементарных исходов испытания, состоящего в бросании игральной кости
{1, 2, 3, 4, 5, 6}.
Эти события образуют полную группу
Слайд 40Вероятность, случайное событие
Вероятность -
количественная мера возможности наступления события.
Если событие A может как
произойти (наступить), так и не произойти в ходе испытания, оно называется случайным. Вероятность случайного события A обозначается P(A). Слайд 41Случайная величина.
С каждым (или несколькими сразу) исходами испытания свяжем
определенное число. Тогда вероятности разных исходов испытания, одновременно являются вероятностями
появления указанных чисел. Все эти числа образуют множество значений некоторой случайной величины.Случайная величина X - величина, которая в результате испытания случайным образом принимает одно из множества своих возможных значений .
Слайд 42
Закон распределения случайной величины содержит информацию о том, какие значения
величина может принимать в результате испытания и какие вероятности соответствуют
ее различным значениям.Слайд 43Пример: Закон распределения случайной величины X – числа очков, выпавших
при броске игральной кости
Слайд 44Статистическое определение вероятности.
Вероятность события оценивается на основе доли
тех
испытаний серии, в которых событие произошло.
Слайд 45Классическое определение вероятности.
Вероятность события равна доле элементарных исходов
испытания, при
которых событие наступает.
Слайд 46 При непосредственном расчете вероятности в
соответствии с классическим определением могут оказаться полезными следующие формулы комбинаторики:
Формула для подсчета числа размещений
Формула для подсчета числа перестановок
Формула для подсчета числа сочетаний
Слайд 50Определение вероятности с помощью теории множеств.
Вероятность события равна сумме вероятностей
элементарных исходов испытания, при которых данное
событие наступает.
Слайд 51 Геометрическое определение вероятности.
Вероятность определяется
отношением геометрических показателей, характеризующих область наступления события и область всех
возможных исходов испытания.Слайд 52 Рассмотрим испытание, состоящее в случайном размещении
точки в прямоугольнике заданного размера. Наступлению события A соответствует попадание
точки в соответствующую область. Графическое изображение такого испытания носит название диаграммы Венна. Для определения вероятности наступления события A необходимо площадь фигуры А поделить на площадь всего многоугольника .Слайд 54 Известные вероятности относительно простых событий
можно использовать при расчете вероятностей более сложных событий, полученных путем
применения определенных операций к исходным событиям.Такими операциями являются умножение, сложение, отрицание и т.д.
Слайд 58 Невозможные и достоверные события.
Вероятность невозможного
события всегда 0, вероятность достоверного события всегда 1.
Если одно из
событий A и B является достоверным (или невозможным), события независимы.Слайд 62Вероятность суммы несовместных событий.
Несовместные события - те, что не
могут наступить одновременно в результате испытания. В этом случае их
произведение является невозможным событием. На рисунке б) события A и B несовместны, AB – невозможное событие: AB = , поэтому P (AB)=P ()=0 и Несовместные возможные события зависимы
Слайд 63 Противоположные события.
Примером противоположных событий могут служить невозможное и достоверное
событие.Слайд 64 Противоположные события всегда образуют полную
группу событий.
Вероятность противоположного события
Слайд 71 Математическое ожидание и дисперсия для
случайной величины X, распределенной по биномиальному закону.
Слайд 72 Математическое ожидание и дисперсия суммы
случайных величин.
При вычислении характеристик биномиального распределения мы использовали свойства
дисперсии и математического ожидания случайных величин, полученных в результате суммирования. Слайд 78
В случае, если распределение случайной величины
подчиняется нормальному закону с параметрами M(X)=a0, 1, вероятность
попасть на заданный интервал вычисляется по формуле:P(x1 x x2)=((x2- a)/)- ((x1- a)/),
где
x
(x)= 1/(2)0.5e-t2/2dt
0
- функция Лапласа.