Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорія ймовірностей -
Содержание
- 1. Теорія ймовірностей -
- 2. ТЕОРІЙ ЙМОВІРНОСТЕЙ. НАВІЩО?
- 3. У сучасному світі автоматизації виробництва теорія ймовірності
- 4. Основні поняття теорії ймовірностей Теорія ймовірностей вивчає
- 5. Експеримент - дослід, випробування, спостереження, виміри, результати
- 6. Класифікація подійВИРОГІДНІ –події, які обов’язково відбудуться під
- 7. Неможливе подія ніколи не відбувається в
- 8. КЛАСИФІКАЦІЯ ПОДІЙКидають два гральних кубіки:а) на першому
- 9. Ви відкрили книгу на будь-якій сторінці і
- 10. ВЗАЄМОЗВ’ЯЗОК ПОДІЙ
- 11. Вкажіть які з описаних пар подій є
- 12. а) настав ранок;б) сьогодні за розкладом 5
- 13. Чи сумісні наступні події?а) вийнята карта червоної
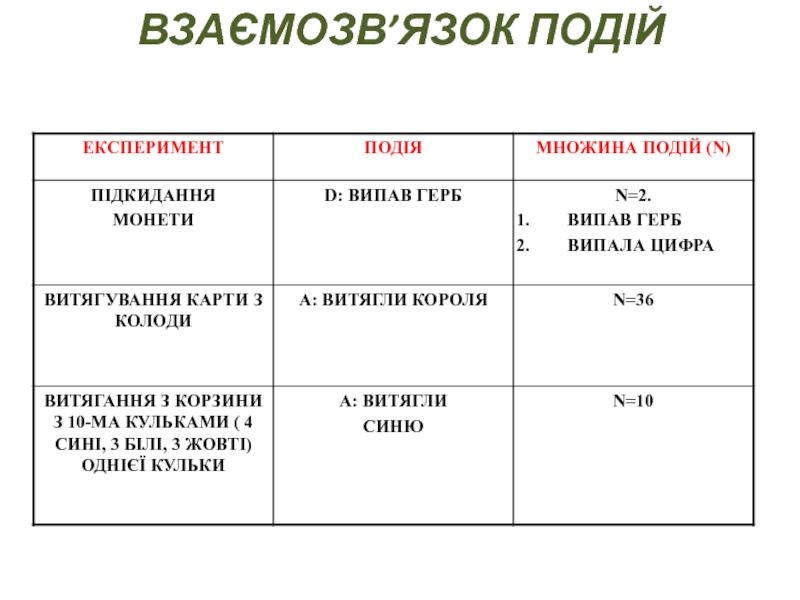
- 14. ВЗАЄМОЗВ’ЯЗОК ПОДІЙ
- 15. ВЗАЄМОЗВ’ЯЗОК ПОДІЙДва студенти одночасно складають іспит незалежно
- 16. МЕТОДІ ЗБОРУ СОЦІОЛОГІЧНИХ ДАНИХОсновні вимоги до експерименту:
- 17. ВЗАЄМОЗВ’ЯЗОК ПОДІЙПовна група подій - кілька подій
- 18. ВЗАЄМОЗВ’ЯЗОК ПОДІЙ
- 19. A1
- 20. Сумою А+В двох подій А та В
- 21. Добутком АВ двох випадкових подій називається подія,
- 22. Різницею А\B подій А та В називають
- 23. Приклад. Підкидання грального кубіка. Нехай подія А
- 24. ЯК ОБЧИСЛЮВАТИ ІМОВІРНІСТЬ ПОДІЙ?
- 25. АЛГОРИТМ обчислення ймовірності події за класичною
- 26. Отже, за умови рівноможливості елементарних подій, що
- 27. Кинуто 2 гральних кубіки. Яка ймовірність подій:
- 28. Набираючи номер телефону ви забули останню цифру
- 29. ОБЧИСЛЕННЯ ЙМОВІРНОСТІ. ПРИКЛАДУ коробці є 3 кубіки:
- 30. Наслідок 1. Якщо ймовірності незалежних подій А1,
- 31. ЗДІЙСНЕННЯ ПРИНАЙМНІ ОДНІЄЇ З НЕЗАЛЕЖНИХ ПОДІЙ. ЗАДАЧАРозв’язанняНехай
- 32. Теорема. Ймовірність суми двох несумісних подій А
- 33. В урні лежать 2 зелених, 3 червоних
- 34. Знайти ймовірність одночасного випадання 3-х очок на
- 35. Взаємно незалежними називаються такі випробування, в яких
- 36. Наслідок 1. Імовірність того, що подія А
- 37. Яка ймовірність того, що при 7 кидках
- 38. Число, яке виражає ймовірність події В за
- 39. В урні 5 білих і 7
- 40. Нехай n — кількість усіх випробувань в
- 41. .Із 10 000 довільно вибраних деталей приблизно 50
- 42. нітак Вибір формулиЧи здійснюються всі події
- 43. ФОРМУЛА ПОВНОЇ ЙМОВІРНОСТІ Формула Байєса
- 44. ФОРМУЛА ПОВНОЇ ІМОВІРНОСТІНаслідком теорем додавання та множення
- 45. АН1Н2Н3Н4НnНехай деяка подія А може відбутись з
- 46. На попередньому слайді використали формулу яка є
- 47. Підводний човен випускає по атакуючому кораблю торпеду.
- 48. З 10 пістолетів приведені до нормального бою
- 49. Розглянемо події:Подія А – студент відповів на
- 50. Формула БайесаНаслідком теореми множення і формули повної
- 51. ймовірність i -тої гіпотезиПовна група несумісних гіпотезH1,
- 52. Знайдемо ймовірність події А за формулою повної
- 53. ЯК ВСЕ ЦЕ ЗАСТОСОВУВАТИ НА ПРАКТИЦІ?НАВІЩО ПОТРІБНІ ФОРМУЛИ БАЙЄСА І НЕ ТІЛЬКИ?
- 54. Наприклад, припустімо, що хтось цікавиться, чи має
- 55. У байєсовій інтерпретації ймовірність вимірює міру впевненості.
- 56. МЕДИЦИНА Далі, уявімо, що ми з'ясували, що тій
- 57. МЕДИЦИНА Може стати несподіванкою, що хоча перебування у
- 58. Припустімо, що тест на вживання наркотиків має
- 59. ПОГАНІ ЗВИЧКИ Цей несподіваний результат виникає тому, що
- 60. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Теорія ймовірностей -
розділ математики, що вивчає закономірності випадкових явищ, які
спостерігаються при багаторазових повтореннях випробувань
Слайд 3 У сучасному світі автоматизації виробництва теорія ймовірності необхідна фахівцям для
вирішення завдань, пов'язаних з виявленням можливого ходу процесів, на які
впливають випадкові чинники.Виникла теорія ймовірностей в 17 столітті. Вперше згадувалась під час листування Б. Паскаля і П.Ферма, які проводили аналіз азартних ігор.
Радянські та російські вчені також зробили значний внесок у дослідження цього розділу математики: П.Л. Чебишев, А.А. Марков, А.М. Ляпунов, А.Н. Колмогоров.
Слайд 4Основні поняття теорії ймовірностей
Теорія ймовірностей вивчає масові випадкові події,
які характеризуються стійкою частотою їх появи.
Слайд 5Експеримент - дослід, випробування, спостереження, виміри, результати яких залежать від
випадку і які можна повторити багато разів в однакових умовах.
Основні
поняття теорії ймовірностей Слайд 6Класифікація подій
ВИРОГІДНІ –
події, які обов’язково відбудуться під час даного експерименту
позначаються
-
Неможливі –
події, які не можуть ніколи відбутися
позначаються
Випадкові –
події,
яка при повторенні досвіду іноді відбуваються, іноді ніпозначаються - A, B, C, D ...
Слайд 7
Неможливе подія ніколи не відбувається в результаті спостереження або
випробування.
Наприклад. Якщо в кошику тільки персики, то дістати з кошика
персик є достовірною подією, а дістати лимон є неможливою подією.КЛАСИФІКАЦІЯ ПОДІЙ. НЕМОЖЛИВІ
Слайд 8КЛАСИФІКАЦІЯ ПОДІЙ
Кидають два гральних кубіки:
а) на першому кубіку випало 3,
а на другому – 5 ;
б) сума отриманих на двох
кубіках очків дорівнює 1;в) сума отриманих на двох кубіках очків дорівнює 13;
г) на обох кубіках випало по 3 очки ;
д) сума очків на двох кубіках менше 15.
Випадкова подія - це така подія, яка в результаті спостереження або випробування може статися, а може і не відбутися.
Приклад.
Студент складає іспит. Іспит складено. Ця подія випадкова, тому що студент міг і не скласти іспит.
Завтра буде дощ. Подія випадкова тому, що дощ може як піти, так і не піти
Гра в лотерею. Можна щось виграти, а можна і не виграти.
Слайд 9Ви відкрили книгу на будь-якій сторінці і прочитали перший-ліпший іменник.
Виявилося що:
а) у складі обраного слова є голосна буква;
б) у
складі обраного слова є буква «О»;в) у складі обраного слова немає голосних букв;
г) у складі обраного слова є м'який знак.
КЛАСИФІКАЦІЯ ПОДІЙ. НЕМОЖЛИВІ
Слайд 11Вкажіть які з описаних пар подій є сумісними, а які
несумісними.
З набору доміно вийнята одна кісточка, на ній:
а) одне число
очок більше 3, інше число 5;б) одне число не менше 6, інше число не більше 6;
в) одне число 2, сума обох чисел дорівнює 9;
г) обидва числа більше 3, сума чисел дорівнює 7.
Події «Кинуто гральний кубік».
На верхній грані виявилося «6 очок», «парне число очок» - сумісні.
Події «Кинута гральна кістка». На верхній грані виявилося «6 очок», «5 очок» - несумісні.
ВЗАЄМОЗВ’ЯЗОК ПОДІЙ
Слайд 12
а) настав ранок;
б) сьогодні за розкладом 5 пар;
в) сьогодні перше
січня;
г) температура повітря в Киеві + 20º С
З подій скласти
пари і виявити серед них пари сумісних та несумісних подій:а) йде дощ;
б) на небі немає жодної хмаринки;
в) настало літо.
ВЗАЄМОЗВ’ЯЗОК ПОДІЙ
Слайд 13Чи сумісні наступні події?
а) вийнята карта червоної масті і вийнято
валета;
б) вийнято короля і вийнято туза.
Чи сумісні наступні події?
1) А
– у, випадковим чином, складеного квадратного рівняння є дійсні корені; Б - дискримінант рівняння від'ємний;
2) А – у, випадковим чином, складеного квадратного рівняння немає дійсних коренів;
Б - дискримінант рівняння не додатній.
Слайд 15ВЗАЄМОЗВ’ЯЗОК ПОДІЙ
Два студенти одночасно складають іспит незалежно один від одного.
Ця подія сумісна і незалежна.
Працівник отримає оплату праці в залежності
від якості її виконання.Слайд 16МЕТОДІ ЗБОРУ СОЦІОЛОГІЧНИХ ДАНИХ
Основні вимоги до експерименту: в якості контрольних
характеристик обирають найважливіші з точки зору досліджуваної проблеми, зміна контрольних
характеристик повинна залежати від тих характеристик експериментальної групи (або середовища проведення експерименту), які вводяться або змінюються самим дослідником. Такі характеристики називаються - факторними. На хід експерименту не повинні впливати ті явища, які не належать до експериментальної ситуації, але потенційно здатні змінити їїСлайд 17ВЗАЄМОЗВ’ЯЗОК ПОДІЙ
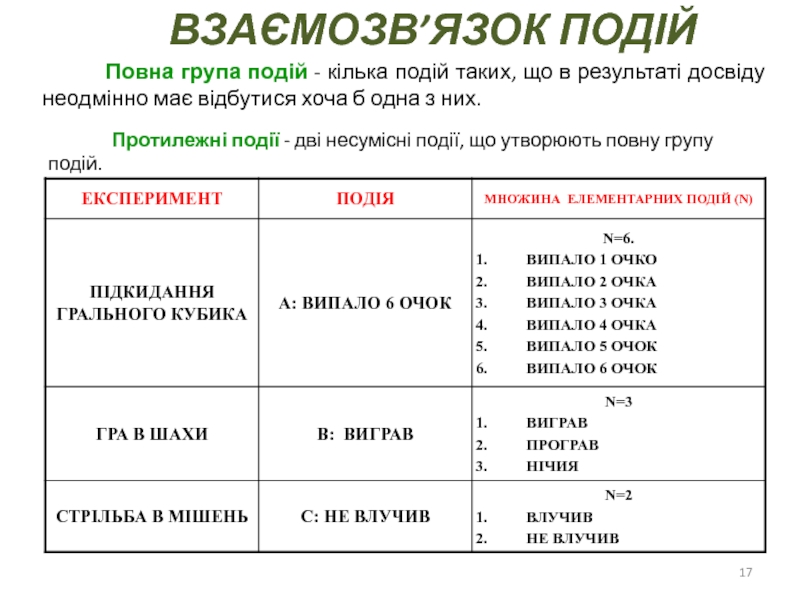
Повна група подій - кілька подій таких, що в
результаті досвіду неодмінно має відбутися хоча б одна з них.
Протилежні
події - дві несумісні події, що утворюють повну групу подій.Слайд 19 A1
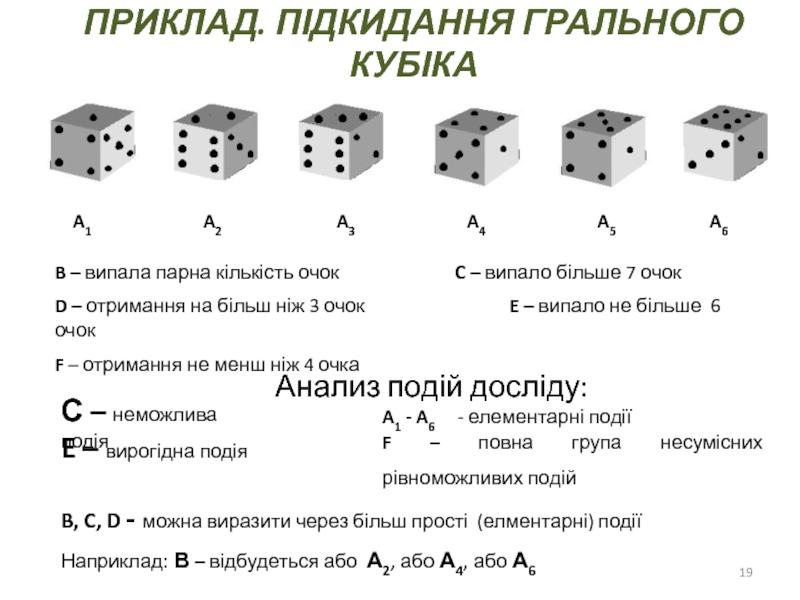
A2 A3 A4 A5 A6
B – випала парна кількість очок C – випало більше 7 очок
D – отримання на більш ніж 3 очок E – випало не більше 6 очок
F – отримання не менш ніж 4 очка
Анализ подій досліду:
С – неможлива подія
E – вирогідна подія
A1 - A6
- елементарні події
B, C, D - можна виразити через більш прості (елментарні) події
Наприклад: В – відбудеться або А2, або А4, або А6
F – повна група несумісних рівноможливих подій
ПРИКЛАД. ПІДКИДАННЯ ГРАЛЬНОГО КУБІКА
Слайд 20Сумою А+В двох подій А та В називають подію, яка
полягає у тому, що в результаті стохастичного експерименту відбувається хоча
б одна із подій.Сумою декількох подій (А1, А2, …,Аn ), відповідно, називається подія, яка полягає в тому, що відбулася хоча б одна із подій (А1, А2, …,Аn ).
Позначення: А1+ А2 +…+Аn = А1 А2 … Аn
Приклад 1. Два стрільці роблять по одному пострілу у мішень. Якщо подія А - влучення першого стрільця, а подія В - другого, то сума А + В - це хоча б одне влучення при двох пострілах.
Приклад 2. Якщо при підкиданні грального кубіка подією Аi називують отримання i очок, то отримання непарного числа очок є сумою подій А1+А2+А3.
АЛГЕБРА ПОДІЙ
Слайд 21Добутком АВ двох випадкових подій називається подія, яка полягає у
тому, що в результаті стохастичного експерименту відбуваються обидві події А
та В.Аналогічно добутком декількох подій (А1, А2, …,Аn) називається подія, яка полягає в тому, що відбулися усі події з (А1, А2, …,Аn)
Позначення: А1·А2 · … ·Аn = А1 А2 … Аn
Приклад 3. В прикладі 1 ( два постріли у мішень) подією АВ буде влучення обох стрільців.
Пример 4. Якщо подія А полягає в тому, що з колоди карт витягнута карта пікової масті, а подія В - в тому, що з колоди витягута дама, то подією АВ буде діставання з колоди дами пік.
АЛГЕБРА ПОДІЙ
Слайд 22Різницею А\B подій А та В називають подію, яка полягає
в тому, що А відбулася, а В – ні.
Пример 5.
Згадаємо приклад 1* про стрільців, де А\ В – влучення першого стрільця при не влученні другого стрілка.Пример 6. В прикладі 4 А\В – витягання з колодибудь-якої карти пікової масті, окрім дами. Навпаки, В\А – витягання дами будь-якої масті, окрім пік.
*(Приклад 1. Два стрільці роблять по одному пострілу по мішені. Подія А – влучення першого стрільця, а подія В - другого).
АЛГЕБРА ПОДІЙ
Слайд 23Приклад. Підкидання грального кубіка. Нехай подія А - «випала парна
кількість очок», а подія В - «випало число більше 3».
Тоді для суми, різниці та добутку події А і В маємо:А + В = {2,4,6} + {4,5,6} = {2,4,5,6},
А-В = {2,4,6}-{4,5,6} = {2},
АВ = {2,4,6}{4,5,6} = {4,6}.
Приклад 2. З таблиці випадкових чисел навмання взято одне число. Подія А - «число ділиться на 5»; подія В - «число закінчується нулем». Що означає подія А - В?
З визначення різниці двох подій А - В випливає, що під цією подією мається на увазі тільки ті результати, які належать безпосередньо події А і не належать події В.
А-В «число, яке ділиться на 5 і не закінчується нулем».
Таке число очевидно має закінчуватися на 5.
АЛГЕБРА ПОДІЙ
Слайд 25АЛГОРИТМ
обчислення ймовірності події
за класичною схемою
Описати експеримент, про який йдеться
в умові задачі та відповідний простір елементарних подій .
Обґрунтувати рівноможливість
елементарних подій і визначити, з яких елементарних подій складається подія А.Визначити кількість т елементарних подій простору Ω.
Визнач кількість k елементарних подій, що сприяють події А.
Обчисли ймовірність події А за формулою
Слайд 26Отже, за умови рівноможливості елементарних подій, що утворюють простір ,
ймовірність будь-якої події А обчислюється за формулою
де
k – кількість
елементарних подій, що сприяють події А, т – кількість усіх елементарних подій простору .
ОБЧИСЛЕННЯ ЙМОВІРНОСТІ
ВЛАСТИВОСТІ
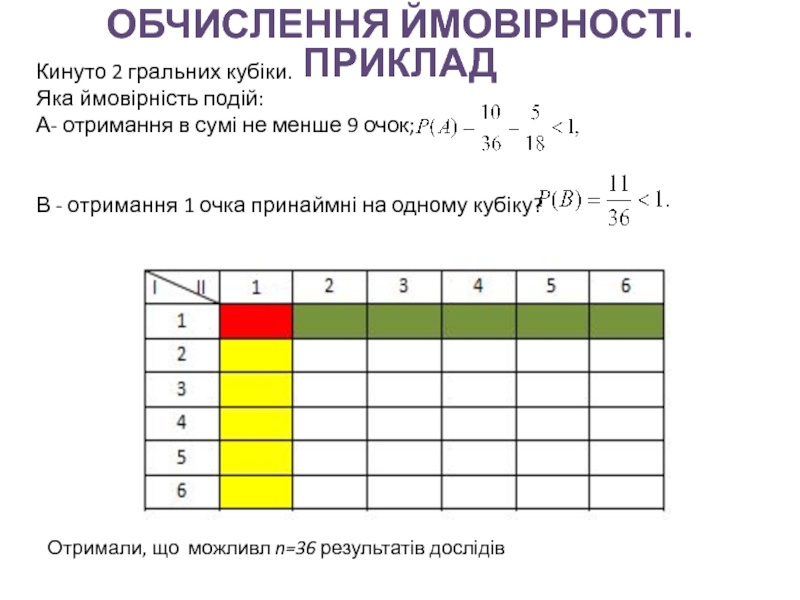
Слайд 27Кинуто 2 гральних кубіки.
Яка ймовірність подій:
А- отримання в
сумі не менше 9 очок;
В - отримання 1 очка
принаймні на одному кубіку?Отримали, що можливл n=36 результатів дослідів
ОБЧИСЛЕННЯ ЙМОВІРНОСТІ. ПРИКЛАД
Слайд 28Набираючи номер телефону ви забули останню цифру та набрали її
навмання. Яка імовірність того, що отримана потрібна цифра?
Відповідь:
0,1ОБЧИСЛЕННЯ ЙМОВІРНОСТІ. ПРИКЛАД
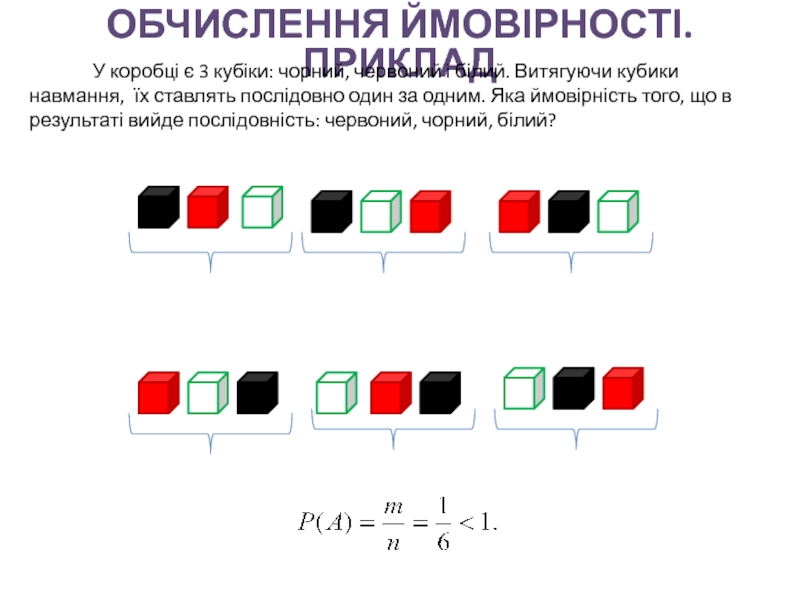
Слайд 29ОБЧИСЛЕННЯ ЙМОВІРНОСТІ. ПРИКЛАД
У коробці є 3 кубіки: чорний, червоний і
білий. Витягуючи кубики навмання, їх ставлять послідовно один за одним.
Яка ймовірність того, що в результаті вийде послідовність: червоний, чорний, білий?Слайд 30Наслідок 1. Якщо ймовірності незалежних подій А1, А2, …, Аn
однакові і рівні р, то ймовірність здійснення принаймні однієї із
нихР(А)=1–(1–р) n.
Теорема. Якщо події А1, А2, А3, …, Аn — незалежні, то ймовірність здійснення принаймні однієї з цих подій може бути виражена через ймовірність цих подій за формулою
Р(А)=1–(1–Р(А1)) (1–Р(А2)) …(1–Р(Аn)).
ЗДІЙСНЕННЯ ПРИНАЙМНІ ОДНІЄЇ З НЕЗАЛЕЖНИХ ПОДІЙ
Слайд 31ЗДІЙСНЕННЯ ПРИНАЙМНІ ОДНІЄЇ З НЕЗАЛЕЖНИХ ПОДІЙ. ЗАДАЧА
Розв’язання
Нехай подія
А —
«стрілок влучить хоча б один раз»
Стрілок робить 4 постріли по
одній і тій же мішені. Ймовірність влучення при одному пострілі дорівнює 0,9. Знайти ймовірність того, що стрілок влучить хоча б один раз.тоді за наслідком з теореми про здійснення принаймні однієї з незалежних подій:
P(A)=1-(1-0,9)4=1-0,14=1-0,0001=0,9999.
Слайд 32Теорема. Ймовірність суми двох несумісних подій А і В дорівнює
сумі ймовірностей цих подій:
якщо АВ=, то Р(А+В)=Р(А)+Р(В). ТЕОРЕМА ПРО ЙМОВІРНІСТЬ СУМИ ПОДІЙ
Наслідок 1. Сума ймовірностей подій А1, А2, …, Аn, які утворюють повну групу і попарно несумісні, дорівнює одиниці:
Р(А1)+Р(А2)+…+Р(Аn)=1.
Наслідок 2. Сума ймовірностей протилежних подій дорівнює одиниці:
Р(А)+Р(Ā)=1.
2
ТЕОРЕМА ПРО ДОБУТОК ПОДІЙ
Добутком подій А і В називається подія С, що полягає в здійсненні обох подій А і В під час одиничного випробування.
Позначається: С=АВ або С=АВ
Теорема. Ймовірність добутку двох незалежних подій А і В дорівнює добутку ймовірностей цих подій:
Р(АВ)=Р(А) Р(В)
Слайд 33В урні лежать 2 зелених, 3 червоних і 6 синіх
кульок.
З неї навмання вибирають 1 кульку. Яка ймовірність того,
що вона не червона?2
ТЕОРЕМА ПРО ЙМОВІРНІСТЬ СУМИ ПОДІЙ. ЗАДАЧА
Розв’язання
Нехай подія
А — «поява червоної кульки», тоді
Ā — «поява не червоної кульки», причому події
А і Ā — протилежні
Слайд 34Знайти ймовірність одночасного випадання 3-х очок на кожному з гральних
кубиків при одному киданні двох кубиків.
2
ТЕОРЕМА ПРО ДОБУТОК ПОДІЙ. ЗАДАЧА
Розв’язання
Нехай
подія А — «випало 3 очки на 1-му кубику»;
В — «випало 3 очки на 2-му кубику», причому події А і В — незалежні
Слайд 35 Взаємно незалежними називаються такі випробування, в яких ймовірність результату кожного
з них не залежить від того, які результати має чи
матиме решта випробувань.Схема Бернуллі: відбувається n незалежних випробувань, у кожному з яких подія А може настати чи не настати.
Ймовірність здійснення події А в кожному з випробуванні однакова і дорівнює р, ймовірність нездійснення події А є q=1–p. Треба знайти ймовірність Pm,n або Pn(m) того, що подія А настане m разів в цих n випробуваннях.
Шукану ймовірність можна обчислити за формулою Бернуллі:
або
НЕЗАЛЕЖНІ ВИПРОБУВАННЯ. СХЕМА БЕРНУЛІ
Слайд 36Наслідок 1. Імовірність того, що подія А відбудеться хоча б
один раз при проведенні n незалежних випробувань, позначається Pn(m ≥
1) і обчислюється за формулоюде p [0;1] — ймовірність настання події А у кожному випробуванні.
Наслідок 2. Найімовірніше значення m0 кількості відбувань події А при проведенні n незалежних випробувань обчислюється за формулою
де p [0;1] — ймовірність настання події А у кожному випробуванні.
НЕЗАЛЕЖНІ ВИПРОБУВАННЯ. СХЕМА БЕРНУЛІ
Слайд 37Яка ймовірність того, що при 7 кидках грального кубика 5
очок випаде рівно 3 рази?
Отже, ймовірність нездійснення події А в
кожному випробуванні також постійна і дорівнює Шукана ймовірність за формулою Бернуллі дорівнює
НЕЗАЛЕЖНІ ВИПРОБУВАННЯ. СХЕМА БЕРНУЛІ
Розв’язання
Нехай подія А — «при одному кидку випаде 5 очок». При кожному кидку ймовірність події А постійна і дорівнює
Слайд 38 Число, яке виражає ймовірність події В за умови, що подія
А вже відбулася, називається умовною ймовірністю події В відносно події
А і позначаєтьсяР(В|А) або PA(B).
Теорема. Ймовірність добутку двох залежних подій дорівнює добутку ймовірності однієї з них на умовну ймовірність другої події, якщо перша подія вже відбулася:
Р(АВ)=РA(B)Р(А).
УМОВНА ЙМОВІРНІСТЬ
Слайд 39 В урні 5 білих і 7 синіх кульок. Навмання
вибирають одну кульку, а потім другу. Знайти ймовірність того, що
із двох вийнятих кульок першою буде біла, а другою — синя.А — «перша взята кулька біла»,
;
подія В — «друга кулька буде синьою», ймовірність події В при умові , що перша — біла
Шукана ймовірність по теоремі множення ймовірностей залежних подій дорівнює
Р(АВ)=РA(B)Р(А)=
Розв’язання
Нехай подія
УМОВНА ЙМОВІРНІСТЬ. ЗАДАЧА
Слайд 40Нехай n — кількість усіх випробувань в окремій серії випробувань,
а m — кількість тих випробувань, у яких відбувається подія
А.Відношення
називається відносною частотою події А в даній серії випробувань. Виявляється, що в різних серіях випробувань відповідні частоти
для великих n практично збігаються, коливаючись навколо деякого сталого значення Р(А), яке називається
статистичною ймовірністю події А:
або
.
СТАТИСТИЧНА ЙМОВІРНІСТЬ
Слайд 41.
Із 10 000 довільно вибраних деталей приблизно 50 бракованих. Скільки приблизно
буде бракованих деталей серед 2800 таких же деталей?
З іншого
боку Звідки,
Відповідь:
Розв’язання
Нехай подія А — «поява бракованої деталі», тоді
СТАТИСТИЧНА ЙМОВІРНІСТЬ
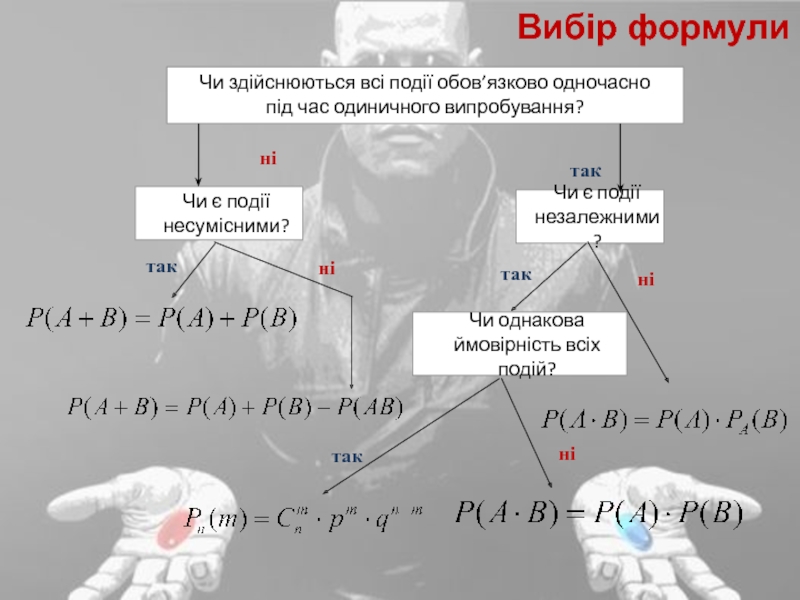
Слайд 42ні
так
Вибір формули
Чи здійснюються всі події обов’язково одночасно
під
час одиничного випробування?
Чи є події несумісними?
Чи є події незалежними?
Чи однакова
ймовірність всіх подій?ні
так
так
ні
так
ні
Слайд 44ФОРМУЛА ПОВНОЇ ІМОВІРНОСТІ
Наслідком теорем додавання та множення ймовірностей є формула
повної ймовірності.
Припустимо, що досліднику потрібно оцінити ймовірність появи якоїсь події
А. З цією метою він висуває ряд несумісних гіпотез (всі можливі рішення), які можуть спричинити за собою подію А. Перед початком експерименту усім висунутим гіпотезам приписуються приблизні ймовірності. Причому кожен дослідник може встановлювати приблизні імовірності виходячи із своїх позицій (грунтуючись на власному або іншому досвіді, наявної в його розпорядженні інформації, статистичних даних або інших можливостях).
Поява події А залежить від різних обставин (гіпотез), тому вводиться поняття - сукупності «умовних ймовірностей» (ймовірностей появи події А при виконанні тієї чи іншої гіпотези). Ці ймовірності також передбачаються дослідником, виходячи з тих же міркувань.
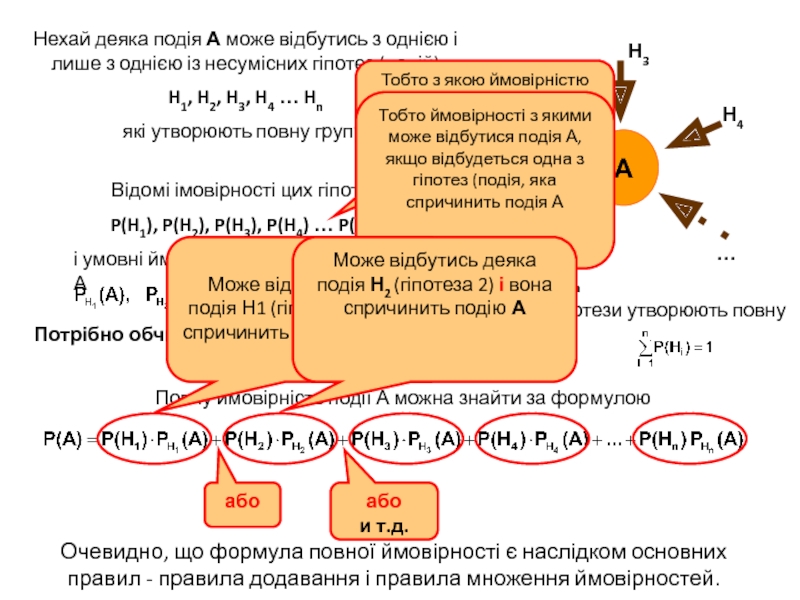
Слайд 45А
Н1
Н2
Н3
Н4
Нn
Нехай деяка подія А може відбутись з однією і лише
з однією із несумісних гіпотез (подій)
H1, H2, H3, H4 …
Hn які утворюють повну групу.
Відомі імовірності цих гіпотез
P(H1), P(H2), P(H3), P(H4) … P(Hn)
Потрібно обчислити повну ймовірність події А.
Повну ймовірність події А можна знайти за формулою
Тобто з якою ймовірністю можуть відбутися ці події (гіпотези)
і умовні ймовірності події А
Тобто ймовірності з якими може відбутися подія А, якщо відбудеться одна з гіпотез (подія, яка спричинить подія А
Може відбутись якась подія Н1 (гіпотеза 1) І вона спричинить за собою подію А
або
Може відбутись деяка подія Н2 (гіпотеза 2) і вона спричинить подію А
або
и т.д.
Очевидно, що формула повної ймовірності є наслідком основних правил - правила додавання і правила множення ймовірностей.
Слайд 46На попередньому слайді використали формулу
яка є формулою повної ймовірності:
де події Н1, Н2, …, Нn попарно несумісні і в
сумі утворюють простір елементарних подій .При цьому події Н1, Н2, …, Нn називають гіпотезами.
ФОРМУЛА ПОВНОЇ ІМОВІРНОСТІ
Слайд 47Підводний човен випускає по атакуючому кораблю торпеду. Ймовірність влучення торпеди
в носову частину корабля дорівнює 0,3; в середню - 0,5;
в кормову - 0,2; промах неможливий. Імовірність затоплення корабля при попаданні в носову частину 0,5, в середню частину - 0,9, в кормову частину - 0,6. Визначити ймовірність затоплення корабля однієї торпедою.Розглянемо події:
Подія А – корабель затоплено;
гіпотеза (подія) Н1 – торпеда влучила в носову частину корабля;
гіпотеза (подія) Н2 – торпеда влучила в середню частину корабля;
гіпотеза (подія) Н3 – торпеда влучила в кормову частину корабля.
Ймовірності гіпотез: Р(Н1)=0,3; Р(Н2)=0,5; Р(Н3)=0,2.
Умовні ймовірності події А:
Імовірність події А за формулою повної ймовірності:
Імовірність затоплення корабля однієї торпедою (при випадковому попаданні в будь-яку частину корабля) в середньому становить 72%.
ФОРМУЛА ПОВНОЇ ІМОВІРНОСТІ. ЗАДАЧА
Слайд 48З 10 пістолетів приведені до нормального бою тільки 4. З
досвіду, ймовірність виконати нормативи зі стрільби з пістолета приведеного до
нормального бою дорівнює 0,8, а з не приведеним до нормального бою - 0,3. Знайти ймовірність того, що курсант виконає нормативи, необхідні для отримання заліку, якщо він стріляє з навмання виданого йому пістолета.
Розглянемо події:
Подія А – норматив виконано;
гіпотеза (подія) Н1 – видано пістолет, який приведений до нормального бою
гіпотеза (подія) Н2 – видано пістолет, який не приведений до нормального бою
Ймовірності гіпотез: Р(Н1) = 0,4; Р(Н2) = 0,6.
Умовні ймовірності події А:
Ймовірність події А за формулою повної ймовірності:
Імовірність виконати нормативи зі стрільби з навмання виданого пістолета в середньому становить 50%.
ФОРМУЛА ПОВНОЇ ІМОВІРНОСТІ. ЗАДАЧА
Слайд 49
Розглянемо події:
Подія А – студент відповів на три поставлених питання;
Гіпотеза
(подія) Н1 – відповів відмінно;
Гіпотеза (подія) Н2 – відповів добре;
Гіпотеза
(подія) Н3 – відповів задовільноГіпотеза (подія) Н4 – відповів погано
До іспиту 6 студентів підготувалися відмінно, 8 - добре, 4 - задовільно і 2 - погано. В екзаменаційних білетах - 40 питань. Відмінно підготовлений студент знає всі питання, добре підготовлений - 32, задовільно - 20, погано - 10. Знайти ймовірність того, що навмання викликаний студент відповість на 3 поставлених йому питання.
Ймовірності гіпотез: Р(Н1)=0,3; Р(Н2)=0,4; Р(Н3)=0,2; Р(Н4)=0,1.
Умовній ймовірності
ІМОВІРНІСТЬ ПОДІЇ А
Імовірність того, що навмання викликаний студент відповість на іспиті на три поставлених йому питання в середньому становить 53%.
ФОРМУЛА ПОВНОЇ ІМОВІРНОСТІ. ЗАДАЧА
Слайд 50Формула Байеса
Наслідком теореми множення і формули повної ймовірності є так
звана
теорема гіпотез або формула Бейєса.
де Н1, Н2, …, Нn гіпотези
і Р(А) ≠ 0.Формула Байєса застосовується, коли необхідно визначити умовні ймовірності гіпотез Н1, Н2, …, Нn за умови, що подія А відбулася і порівняти їх з безумовними чи з іншими умовними ймовірностями
У теорії ймовірностей та статистіці Теоре́ма Ба́єса (або ж Зако́н Ба́єса) описує ймовірність події, спираючись на обставини, що могли би бути пов'язані з цією подією.
Слайд 51ймовірність i -тої гіпотези
Повна група несумісних гіпотез
H1, H2, H3, H4
… Hn .
Умовна ймовірність події А (сумісно із
i – тою
гіпотезою)Ймовірність події А (обчислена за формулою повної ймовірності)
Формула Байеса
Слайд 52Знайдемо ймовірність події А за формулою повної ймовірності:
Ймовірності гіпотез: Р
(Н1) = 0,357; Р (Н2) = 0,5; Р (Н3) =
0,143.Умовні ймовірності події А:
Переоцінку ймовірностей гіпотез про належність стрілка до однієї з груп після випробування проведемо за формулою Байєса:
Як видно з розрахунку, результат випробування змінив ймовірності прийнятих гіпотез і дозволяє зробити висновок про те, що найімовірніше стрілок належить до II групи.
З 14 стрільців 5 потрапляють в мішень з імовірністю 0,8; 7 - з ймовірністю 0,6 і 2 - з ймовірністю 0,5. Навмання обраний стрілок зробив постріл, але в мішень не вцілив. До якої з груп найімовірніше належить цей стрілок?
Розглянемо події:
Подія А – в мішень не влучили;
гіпотеза Н1 – постріл зробив стрілок з першої групи;
гіпотеза Н2 –постріл зробив стрілок з другої групи;;
гіпотеза Н3 – постріл зробив стрілок з третьоїгрупи;.
Формула Байеса
За умовою задачі дано умовні ймовірності влучення в мішень. Отже вірогідність не потрапити в мішень дорівнює
q = 1 – p
Сума ймовірностей гіпотез після випробування, також, як і до випробування, завжди повинна дорівнювати одиниці:
0,208+0,584+0,208=1
Слайд 54Наприклад, припустімо, що хтось цікавиться, чи має рак певна особа,
і знає вік цієї особи. Якщо рак пов'язаний з віком,
то, застосовуючи теорему Баєса, інформацію про вік осіб можливо використати для точнішої оцінки ймовірності того, що вони мають рак.Слайд 55 У байєсовій інтерпретації ймовірність вимірює міру впевненості. Теорема Баєса відтак
пов'язує міру впевненості у висловленні до та після врахування свідчення.
Наприклад, припустімо, що вважається із впевненістю 50%, що монета вдвічі ймовірніше падає орлом, ніж решкою. Якщо монета підкидається кілька разів та спостерігаються результати, то міра впевненості може рости, зменшуватися або залишатися такою ж, у залежності від результатів.
Припустімо, що ми хочемо знати ймовірність того, що якась особа має рак, але ми нічого не знаємо про неї. Незважаючи на відсутність жодних відомостей про особу, якусь імовірність може бути призначено на основі загальної поширеності раку.
Заради цього прикладу уявімо, що нею є 1%. Це є відомим як базовий рівень, або апріорна ймовірність мати рак. «Апріорна» відповідає часу до того моменту, як нас буде поінформовано про даний конкретний випадок.
МЕДИЦИНА
Слайд 56МЕДИЦИНА
Далі, уявімо, що ми з'ясували, що тій особі 65 років.
Якщо припустити, що рак та вік є пов'язаними, то цю
нову порцію інформації може бути використано для кращої оцінки ризику тієї особи мати рак. Точніше, ми хотіли би знати ймовірність того, що особа має рак, якщо відомо, що їй 65 років.Ця величина є відомою як поточна ймовірність, де «поточна» відповідає теоретичній ситуації після з'ясування інформації про даний конкретний випадок.
Для того, щоби застосувати знання про вік тієї особи в поєднанні з теоремою Баєса, потрібні дві додаткові порції інформації. Зауважте, проте, що ця додаткова інформація не стосується конкретно тієї особи. Потрібна інформація є наступною:
1. Ймовірність мати вік 65 років. Припустімо, що нею є 0.2%.
2. Ймовірність того, що особа, яка має рак, має вік 65 років. Припустімо, що нею є 0.5%.
Зауважте, що вона є більшою за попереднє значення. Це відображає той факт, що люди з раком є непропорційно 65-річними.
Слайд 57МЕДИЦИНА
Може стати несподіванкою, що хоча перебування у віці 65 років
і збільшує ризик мати рак, ймовірність тієї особи мати рак
все одно є досить низькою.Це тому, що низьким є базовий рівень раку (незалежно від віку). Це показує як важливість базового рівня, так і те, що ним зазвичай нехтують. Нехтування базовим рівнем призводить до серйозного спотворення інтерпретації статистики; отже, потрібно приділяти особливу увагу тому, щоби уникати таких помилок.
Знайомство з теоремою Баєса є одним із шляхів боротьби з природною схильністю нехтувати базовими рівнями.
Задачі із застосуванням теореми Баєса часто легше зрозуміти, застосовуючи задані в задачі умови до великого набору спостережень.
Припустімо, наприклад, що якась спільнота складається зі 100 000 людей. Відповідно до умови задачі, 1% цієї генеральної сукупності, або 1 000 людей, матимуть рак. 0.2% від цієї генеральної сукупності, або 200 людей, матимуть вік 65 років. Із 1 000 людей з раком лише 0.5%, або 5 людей, будуть 65-річними.
Таким чином, очікується, що з 200 людей, які мають вік 65 років, лише 5 матимуть рак. 5/200 = 2.5%.
Слайд 58Припустімо, що тест на вживання наркотиків має чутливість 99% та
специфічність 99%. Тобто, цей тест даватиме 99% вірних позитивних результатів
для тих, хто вживає наркотики, і 99% вірних негативних результатів для тих, хто не вживає. Припустімо, що 0.5% людей вживають наркотики. Якщо для випадково вибраної особи перевірка виявляється позитивною, то якою є ймовірність, що вона вживає наркотики? Незважаючи на видиму точність перевірки, якщо індивідуальні перевірки дають позитивний результат, то ймовірніше, що вони не вживають наркотиків, ніж що вони їх вживають. Це ще раз свідчить про важливість базових рівнів.
ПОГАНІ ЗВИЧКИ
Слайд 59ПОГАНІ ЗВИЧКИ
Цей несподіваний результат виникає тому, що кількість тих, хто
не вживає, є дуже великою у порівнянні з кількістю тих,
хто вживає; таким чином, кількість хибних позитивних результатів (0.995%) переважує кількість вірних позитивних результатів (0.495%). На конкретних цифрах, якщо перевірено 1000 осіб, то очікується 995 тих, хто не вживає наркотиків, і 5 тих, хто вживає.Із 995 тих, хто не вживає, очікується 0.01 × 995 ≃ 10 хибних позитивних результатів. Із 5 тих, хто вживає, очікується 0.99 × 5 ≃ 5 вірних позитивних результатів. Із 15 позитивних результатів лише 5, близько 33%, є істинними.
Примітка: Важливість специфічності може бути проілюстровано показуванням, що навіть якщо чутливість є 100%, а специфічність є 99%, то ймовірність того, що особа вживає наркотики, є ≈33%, але якщо специфічність змінюється до 99.5%, а чутливість падає до 99%, то ймовірність того, що особа вживає наркотики, виростає до 49.8%.