Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тепловые двигатели и нагнетатели
Содержание
- 1. Тепловые двигатели и нагнетатели
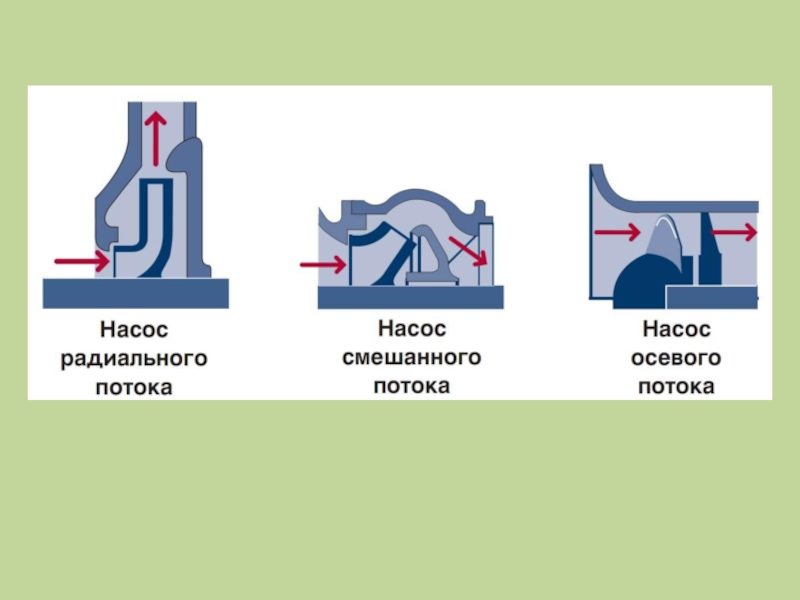
- 2. 1. Способы действия центробежных насосов и вентиляторов
- 3. Передача энергии потоку жидкости с вала центробежной
- 4. Диск 1, называемый основным или ведущим, составляет
- 5. Работа центробежных сил на пути от входа
- 6. Для рассматриваемого случая при z = const
- 7. Равенство (1) показывает, что давление, развиваемое колесом
- 8. В конструкцию центробежной машины кроме рабочего колеса
- 9. Слайд 9
- 10. 2. Уравнение Эйлера. Теоретический и действительный напоры, развиваемые рабочим колесом
- 11. Напор, развиваемый рабочим колесом центробежной машины, зависит
- 12. Введем следующие предположения:Поток имеет струйчатую структуру, т.е.
- 13. Первые два предположения осуществимы при бесконечно большом
- 14. Теоретический момент внешних сил, передаваемый потоку с
- 15. Мощность, передаваемая потоку в межлопастных каналах,(3)Теоретическая мощность
- 16. Удельная работаУдельная работа связана с напором равенством:Теоретическое значение напора определяется по формуле:Теоретическое давление определяется по формуле:(5)(6)
- 17. Основные уравнения центробежной машиныУравнение (5) называется уравнением Эйлера.(5)(3)
- 18. Из параллелограммов на входе и выходе в
- 19. – напор, обусловленный центробежной силы жидкости (газа).–
- 20. Скоростной напор, создаваемый лопастями РК, при принятых
- 21. Если выполнить межлопастные каналы так, что их
- 22. Удельная работа на закручивание передается жидкости и
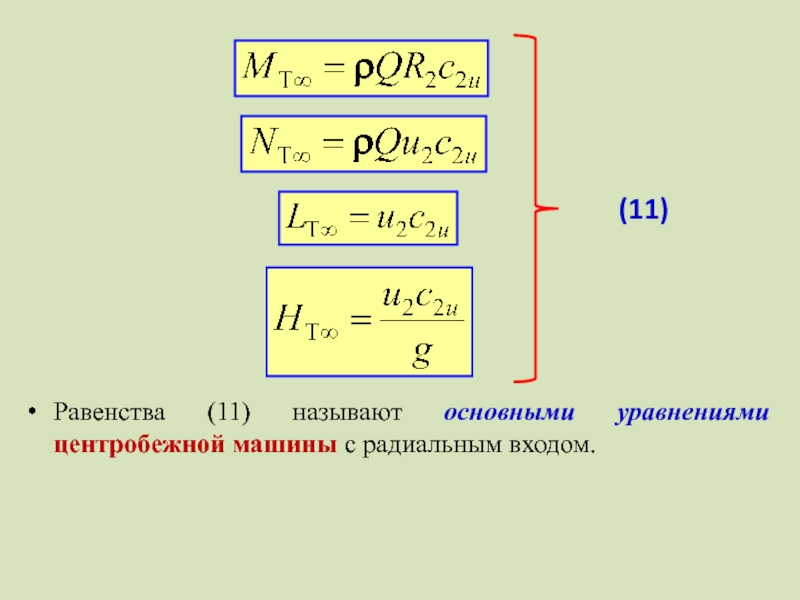
- 23. Равенства (11) называют основными уравнениями центробежной машины с радиальным входом.(11)
- 24. Действительный напор, развиваемый РК, меньше теоретического при
- 25. В действительности скорости w2 распределены по выходному
- 26. Вычисление действительного напора ведется по формулеДля современных
- 27. Формула Стодолы дает удовлетворительные практические результаты.В ориентировочных расчетах принимается μ=0,8.
- 28. 3. Уравнение энергии потока в рабочем колесе
- 29. Закон сохранения энергии газового потока в РК
- 30. Удельная энергия, сообщаемая газуВведем поправочный коэффициент μ,
- 31. Для насосов и вентиляторов (подача газовой среды
- 32. На основании равенства (16) уравнение (15) можно
- 33. Графическое представление баланса энергии центробежной машины.На рисунке
- 34. 4. Кинематика потока в рабочем колесе нагнетателя
- 35. Передачу энергии от привода жидкости осуществляет РК,
- 36. Проанализируем основные закономерности течения жидкости в межлопастном
- 37. Энергия, передаваемая потоку рабочим колесом, определяется значениями
- 38. Вектор окружной скорости u, направленный по касательной
- 39. Пусть на входе в РК (точка 1)
- 40. Из рисунков видно: абсолютную скорость потока можно
- 41. Уравнение Эйлера для работы лопастных нагнетателей, которое
- 42. В реальном вентиляторе часть давления теряется в
- 43. Большое влияние на коэффициент полного давления оказывает
- 44. Удельная полезная (индикаторная) работа, сообщенная потоку вентилятором,
- 45. Мощность на валу (эффективная мощность) Nе обычно
- 46. Статический КПД дополняет оценку эффективности вентилятора, так
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тепловые двигатели и нагнетатели
Центробежные нагнетатели (насосы и вентиляторы). Основы теории
Лекция
№30
Слайд 3Передача энергии потоку жидкости с вала центробежной машины осуществляется рабочим
колесом с кривыми лопастями.
Внутренняя полость рабочего колеса (межлопастные каналы) образуются
двумя фасованными дисками 1 и 2, и несколькими лопастями 3 (обычно кривыми).Слайд 4Диск 1, называемый основным или ведущим, составляет одно целое со
ступицей, служащей для жесткой посадки на вал насоса.
В вентиляторах основной
диск и ступица изготовляются раздельно и жестко соединяются заклепками или сваркой.Диск 2 называется покрывающим или передним. Он составляет одно целое с лопастями в насосах, а в вентиляторах соединяется с лопастями сваркой или заклепыванием.
Жидкость (газ), поступая в межлопастные каналы, вращается вокруг оси 0 – 0 рабочего колеса, под влиянием центробежных сил перемещается к периферии колеса и выбрасывается в канал, окружающее колесо.
Слайд 5Работа центробежных сил на пути от входа в межлопастные каналы
до выхода из них приводит к увеличению энергии потока.
Применим к
потоку в межлопастных каналах вращающегося рабочего колеса с вертикальной осью и постоянной шириной лопасти уравнение Бернулли, полагая потери энергии равными нулю: Слайд 6Для рассматриваемого случая при z = const уравнение Бернулли в
развернутом виде будет иметь вид
Повышение давления в потоке, проходящее через
колесо центробежной машины определяется уравнением:(1)
Слайд 7Равенство (1) показывает, что давление, развиваемое колесом центробежной машины, есть
результат двух процессов:
1) преобразования кинетической энергии относительного движения [первый член
равенства (1)];2) работы центробежных сил [второй член равенства (1)].
Слайд 8В конструкцию центробежной машины кроме рабочего колеса входят следующие основные
элементы:
подвод (входная полость) 5;
отвод (выходная полость) 4.
В некоторых машинах
подвод и отвод выполняются в виде специальных, направляющих поток лопаточных устройств.Слайд 11Напор, развиваемый рабочим колесом центробежной машины, зависит от скорости потока,
проходящее через рабочее колесо, и от размеров его.
Основная задача теории
центробежных машин состоит в установлении зависимости напора от скорости потока и размеров рабочего колеса.Кинематическая структура потока во вращающихся криволинейных каналах весьма сложна, и решение указанной задачи требует введение некоторых условий, упрощающих решение.
Полученный таким образом результат может быть скорректирован введением опытных коэффициентов.
Слайд 12Введем следующие предположения:
Поток имеет струйчатую структуру, т.е. состоит из множества
струй, повторяющих геометрическую форму лопасти;
Имеет место осевая симметрия потока,
т.е. все струи, составляющие поток, совершенно одинаковы геометрически и кинематически;Поток является плоским, т.е. градиент скорости вдоль оси, параллельной геометрической оси машины, отсутствует.
Слайд 13Первые два предположения осуществимы при бесконечно большом количестве работающих лопастей
при условии, что лопасти не имеют толщины и, следовательно, не
уменьшают проходное сечение межлопастных каналов.Параметры машины, вычисляемые при бесконечно большом количестве работающих лопастей, обозначаются индексом ∞ и называются параметрами при бесконечном количестве лопастей.
Слайд 14Теоретический момент внешних сил, передаваемый потоку с вала (в предположении
бесконечного количества лопастей и при отсутствии потерь в процессе преобразования
механической энергии в гидравлическую)где ρQ – массовый расход через
колесо; l1 и l2 – плечи скоростей
с1 и с2.
(2)
Слайд 15Мощность, передаваемая потоку в межлопастных каналах,
(3)
Теоретическая мощность (при бесконечном количестве
лопастей) может быть вычислена как произведение массы, проходящей через рабочее
колесо в секунду, на соответствующую удельную работу:(4)
Слайд 16Удельная работа
Удельная работа связана с напором равенством:
Теоретическое значение напора определяется
по формуле:
Теоретическое давление определяется по формуле:
(5)
(6)
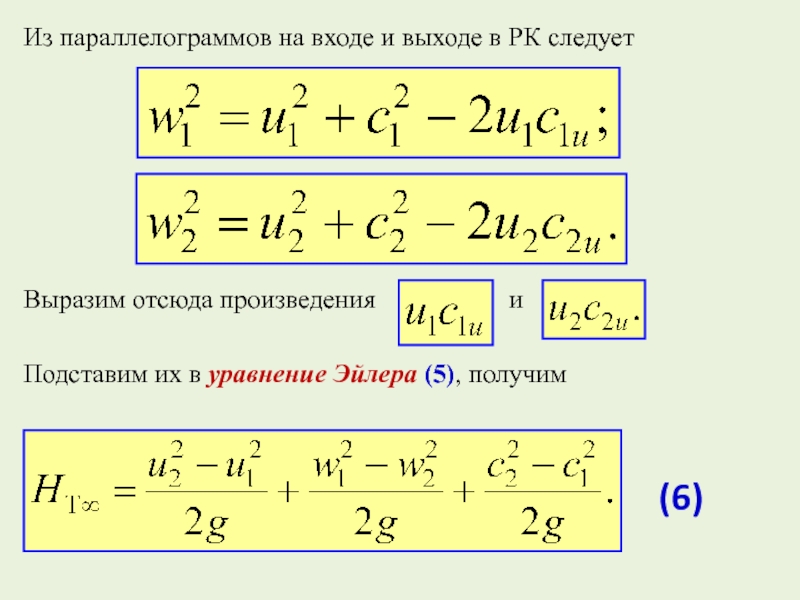
Слайд 18Из параллелограммов на входе и выходе в РК следует
Выразим отсюда
произведения
иПодставим их в уравнение Эйлера (5), получим
(6)
Слайд 19– напор, обусловленный центробежной силы жидкости (газа).
– прирост напора вследствие
преобразования кинетической энергии относительного движения межлопастных каналах.
– прирост напора вследствие
преобразования кинетической энергии абсолютного движения межлопастных каналах.Слайд 20Скоростной напор, создаваемый лопастями РК, при принятых ранее допущениях равен:
Теоретический
статистический напор составляет:
Из равенства (8) следует, что повышение статистического напора
и давления лопастным колесом центробежной машины происходит за счет работы центробежных сил и понижения кинетической энергии относительного движения.(7)
(8)
Слайд 21Если выполнить межлопастные каналы так, что их сечения по всей
длине будет постоянно, то w1=w2 и теоретическое статическое давление, развиваемое
таким колесом равно:Тангенциальная составляющая абсолютной скорости c1u характеризует закрученность потока перед входом в межлопастные каналы.
Удельная работа, затрачиваемая на закручивание, равна:
(9)
Слайд 22Удельная работа на закручивание передается жидкости и суммируется с работой,
передаваемой потоку рабочими лопастями. Удельная теоретическая энергия потока на выходе
из РК равна:При определении теоретических параметров машин, не имеющих на входе специальных устройств, закручивающих поток, основные уравнения представляются в следующем виде:
(10)
(11)
Слайд 24Действительный напор, развиваемый РК, меньше теоретического при бесконечно количестве лопастей,
Это
объясняется тем, что,
во-первых, часть энергии, получаемой потоком в межлопастных каналах,
затрачивается на преодоление гидравлического сопротивления проточной полости машины (это обстоятельство учитывают введением в расчет гидравлического КПД ηг, оценивающее совершенство проточной полости машины);во-вторых, уравнение Эйлера
получено в предположении осевой симметрии потока, т.е. при постоянном осредненном значении w2 на выходе из межлопастных каналов.
Слайд 25В действительности скорости w2 распределены по выходному сечению РК неравномерно,
и поэтому переход от НТ∞ к НТ может быть проведен
по формулегде μ<1 – поправочный коэффициент, учитывающий количество лопастей.
Уравнение Эйлера давало бы точное значение НТ в случае, когда при составлении уравнения (2) импульс потока вычислялся не по среднему значению w2=const, а с учетом действительного распределения скоростей в выходном сечении колеса.
(12)
Слайд 26Вычисление действительного напора ведется по формуле
Для современных центробежных машин ηг
= 0,80÷0,96.
Для определения поправочного коэффициента μ пользуются формулой чешского профессора
Стодолыгде z – количество лопастей РК насоса.
(13)
Слайд 27Формула Стодолы дает удовлетворительные практические результаты.
В ориентировочных расчетах принимается μ=0,8.
Слайд 283. Уравнение энергии потока в рабочем колесе машины
В машинах, перемещающие
газы, ρ = var и передача энергии потоку и теплообмен
с окружающей средой обуславливает изменение термодинамического состояния газа.Слайд 29Закон сохранения энергии газового потока в РК центробежной машины можно
записать в виде:
где соответственно для входа и выхода РК:
T1 и
T2 – абсолютные температуры газа;c1 и c2 – абсолютные скорости;
cp – теплоемкость газа при постоянном давлении;
LT – удельная энергия, сообщаемая газу;
q – количество теплоты, переходящее в окружающую среду, отнесенное к 1 кг газа.
(14)
Слайд 30Удельная энергия, сообщаемая газу
Введем поправочный коэффициент μ, получаем
Это уравнение показывает,
что механическая работа, передаваемая рабочими лопастями потоку газа, расходуется на
изменение состояния газа, приращение его кинетической энергии и частично теряется, переходя в среду, окружающую машину, в виде теплоты.(15)
Слайд 31Для насосов и вентиляторов (подача газовой среды при небольшом повышении
давления), то термодинамическое состояние потока можно полагать неизменяющимся. Температура газа
(жидкости) в процессе работы машины остается постоянной, и баланс энергии может быть записан в следующем виде:где р1 и р2 – давление на входе в РК и выходе; h – потери напора в проточной полости машины.
(16)
Слайд 32На основании равенства (16) уравнение (15) можно записать:
Следовательно, механическая работа,
сообщаемая потоку рабочими лопастями машины, повышает давление в потоке, увеличивает
кинетическую энергию его и отчасти расходуется на преодоление сопротивления проточной полости.(17)
Слайд 33Графическое представление баланса энергии центробежной машины.
На рисунке обозначено:
L1 – удельная
энергия потока на входе в РК;
Lк – удельная энергия, передаваемая
потоку в РК;L2 – удельная энергия потока на выходе из РК;
Lокр.ср – потеря энергии в окружающую среду.
Баланс энергии рабочего колеса центробежной машины
Слайд 344. Кинематика потока в рабочем колесе нагнетателя (упрощенная теория)
Конструкция рабочего
колеса насоса или вентилятора представляет собой систему лопаток, заканчивающихся острой
кромкой. Лопатки закреплены между двумя дисками, один из которых насажен на вал, соединенный с валом электродвигателя. При вращении рабочего колеса каждая лопатка вследствие циркуляционного обтекания, взаимодействуя с потоком, вызывает появление реакции, равной по величине подъемной силе. Суммарная сила воздействия лопаток на поток будет равна сумме реакций каждой лопатки.Слайд 35Передачу энергии от привода жидкости осуществляет РК, состоящее из переднего
1 и заднего 2 дисков (рисунок), между которыми с одинаковым
шагом установлены лопатки 3. Меридиональное сечение рабочего колеса характеризуется двумя параметрами: b1 – ширина при входе жидкости на лопатки; b2 – ширина на выходе. Лопатки РК обычно имеют цилиндрическую форму; их устанавливают перпендикулярно плоскости заднего диска.Схематический разрез рабочего колеса радиального вентилятора:
1 – передний диск; 2 – задний диск; 3 – лопатка
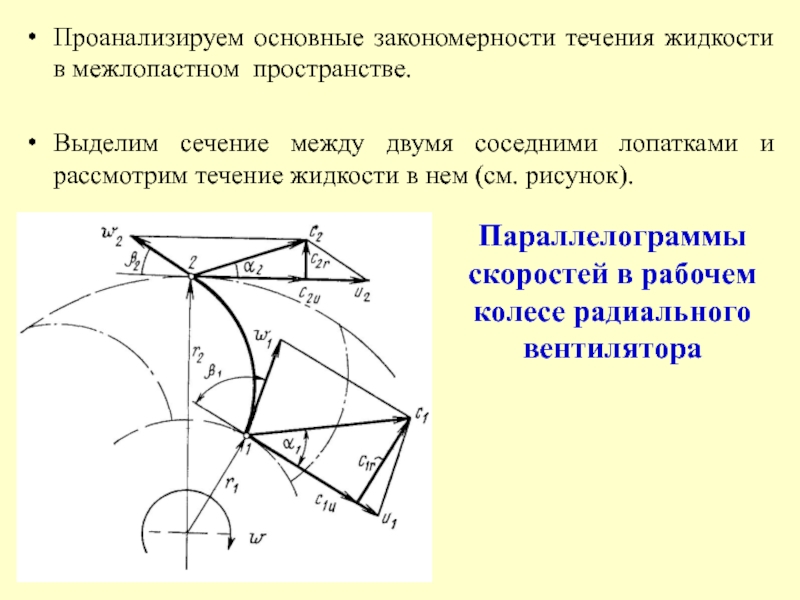
Слайд 36Проанализируем основные закономерности течения жидкости в межлопастном пространстве.
Выделим сечение между
двумя соседними лопатками и рассмотрим течение жидкости в нем (см.
рисунок).Параллелограммы скоростей в рабочем колесе радиального вентилятора
Слайд 37Энергия, передаваемая потоку рабочим колесом, определяется значениями абсолютных с, относительных
w и окружнных u скоростей при входе и выходе из
межлопастного пространства.Абсолютная скорость с – это скорость движения потока относительно неподвижного корпуса турбины (нагнетателя). Абсолютная скорость равна геометрической сумме относительной w и переносной (окружной) u скоростей.
Относительная скорость w – это скорость движения потока относительно вращающегося диска турбины (нагнетателя). Вектор ее направлен по касательной к кромке на выходе или входе в устройства турбины.
Слайд 38Вектор окружной скорости u, направленный по касательной к данной точке
устройства турбины (нагнетателя).
Векторы окружной и абсолютной скоростей образуют угол α;
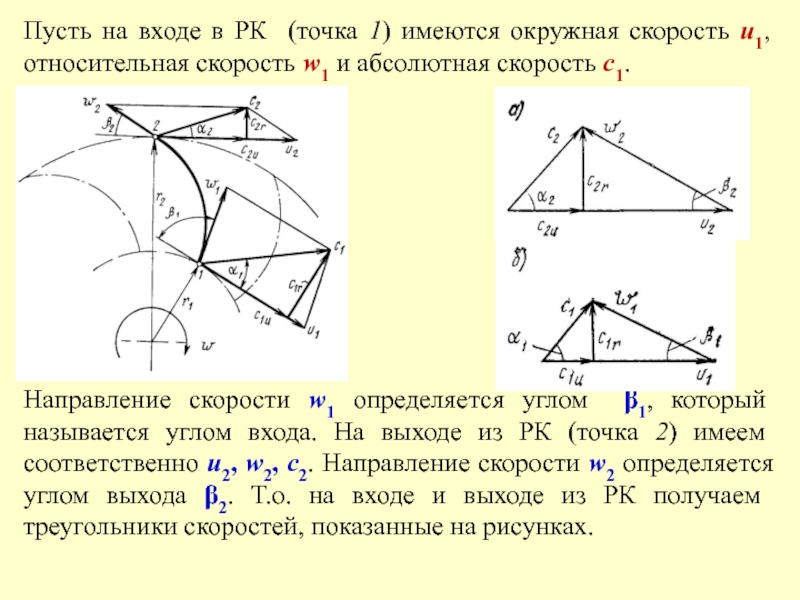
вектор относительной и окружной скоростей – угол β.Слайд 39Пусть на входе в РК (точка 1) имеются окружная скорость
u1, относительная скорость w1 и абсолютная скорость с1.
Направление скорости w1
определяется углом β1, который называется углом входа. На выходе из РК (точка 2) имеем соответственно u2, w2, с2. Направление скорости w2 определяется углом выхода β2. Т.о. на входе и выходе из РК получаем треугольники скоростей, показанные на рисунках.Слайд 40Из рисунков видно: абсолютную скорость потока можно разложить на радиальную
составляющую, равную сr = с·sinα, и окружную (тангенциальную) составляющую сu
= с·cosα, называемую скоростью закручивания.Вектор окружной скорости направленный по касательной к данной точке рабочего колеса радиусом r в сторону вращения рабочего колеса, вращающегося с угловой скоростью ωо, равен:
Слайд 41Уравнение Эйлера для работы лопастных нагнетателей, которое с учетом радиального
входа потока (с1u =0) имеет выражение в виде:
Теоретическое давление вентилятора
где
ρ – средняя плотность перемещаемого газа, кг/м3.это уравнение определяет теоретический напор вентилятора (насоса).
Слайд 42В реальном вентиляторе часть давления теряется в проточной части. Если
оценить эти потери давления гидравлическим КПД ηг = 0,6 ÷
0,9, то действительное давление вентилятора:Произведение
называется коэффициентом полного давления.
С учетом последней формулы получаем:
Слайд 43Большое влияние на коэффициент полного давления оказывает угол β2. В
зависимости от типа лопастей угол β2 изменяется в пределах от
10 до 150º, в связи с чем изменяется почти в 3 раза, от 0,35 до 1,2.Полное давление вентилятора определяют при испытаниях головного образца машины:
где р1ст, р2ст – статическое давление потока соответственно на входе и выходе вентилятора; с1 и с2 – соответствующие скорости потока.
Слайд 44Удельная полезная (индикаторная) работа, сообщенная потоку вентилятором, Дж/кг,:
Полезная мощность вентилятора,
кВт,
где Vо – объемная подача вентилятора, м3/с.
Объемная подача вентилятора Vо
определяется из выражения, м3/с,Слайд 45Мощность на валу (эффективная мощность) Nе обычно определяется при испытании
вентилятора.
Вентиляторы характеризуются двумя КПД: полным
и статическим
где рст = р2ст –
р1ст. Слайд 46Статический КПД дополняет оценку эффективности вентилятора, так как в полной
энергии, сообщаемой потоку газа, существенную долю составляет кинетическая энергия. Ориентировочно
ηст меньше η на 20 – 30%.Мощность привода вентилятора, Вт, выбирается с запасом на возможные отклонения от расчетного режима:
где ηпер – КПД передачи; при непосредственном соединении вентилятора и привода ηпер = 1,0, при клиноременной передаче ηпер = 0,92.