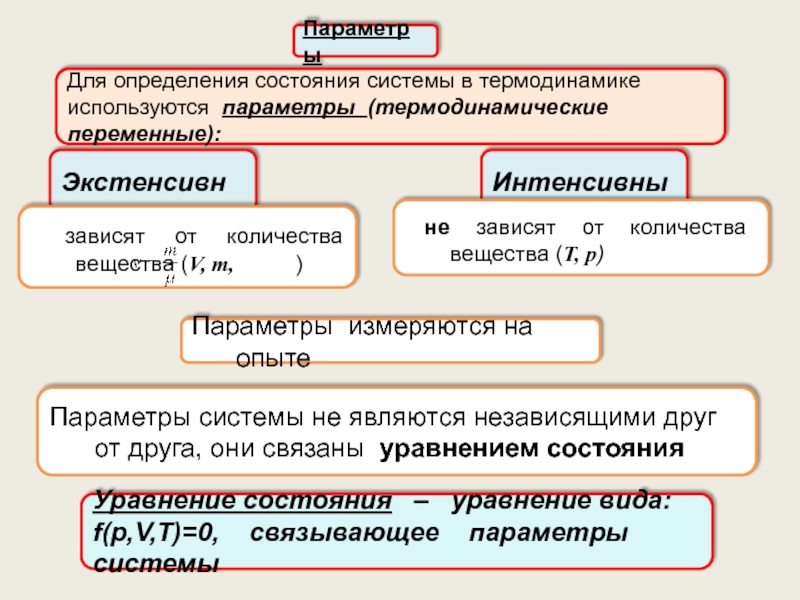
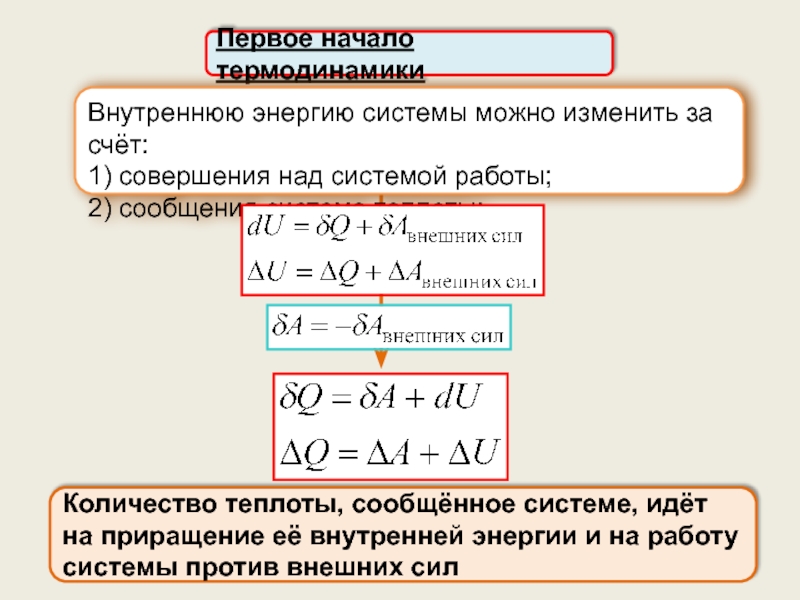
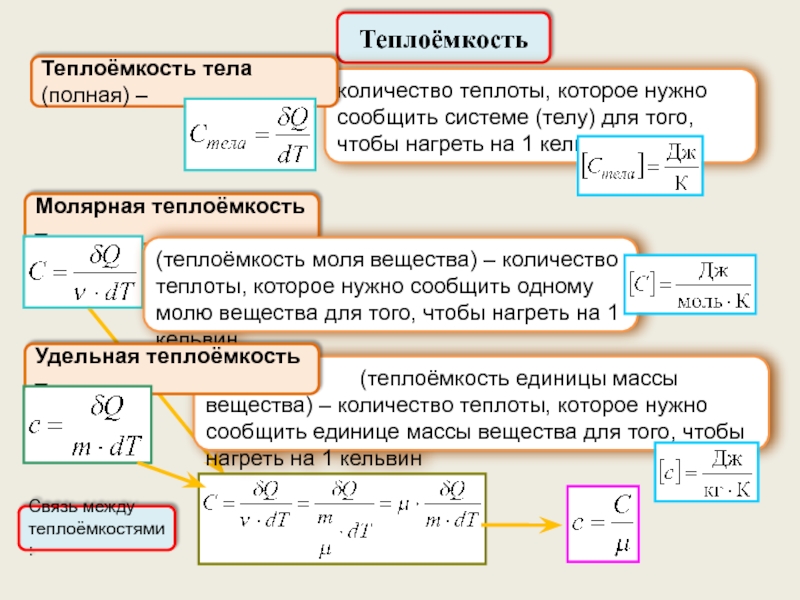
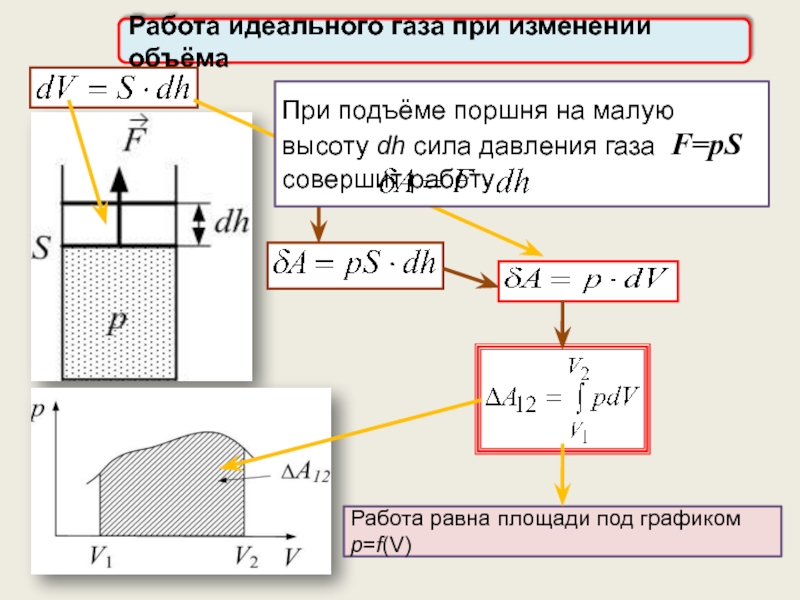
Теплоёмкость.
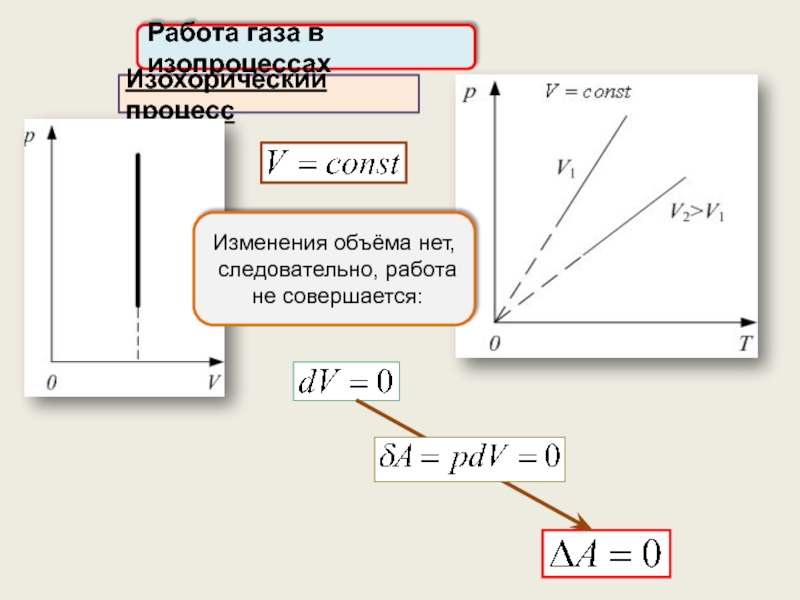
Работа идеального газа в изопроцессах.
1) Изохорический процесс 2) Изобарический процесс. Уравнение Майера
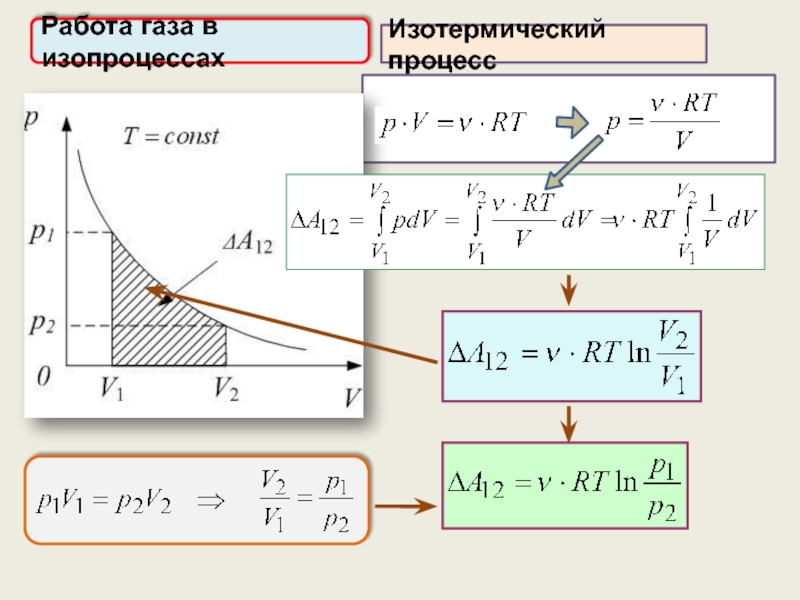
3) Изотермический процесс
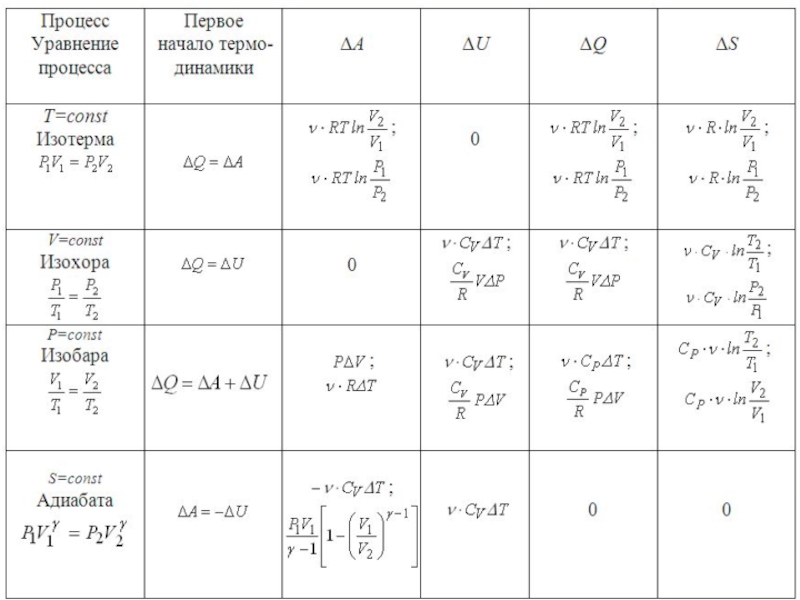
5. Применение первого начала термодинамики к изопроцессам
1) Изохорический процесс
2) Изобарический процесс
3) Изотермический процесс
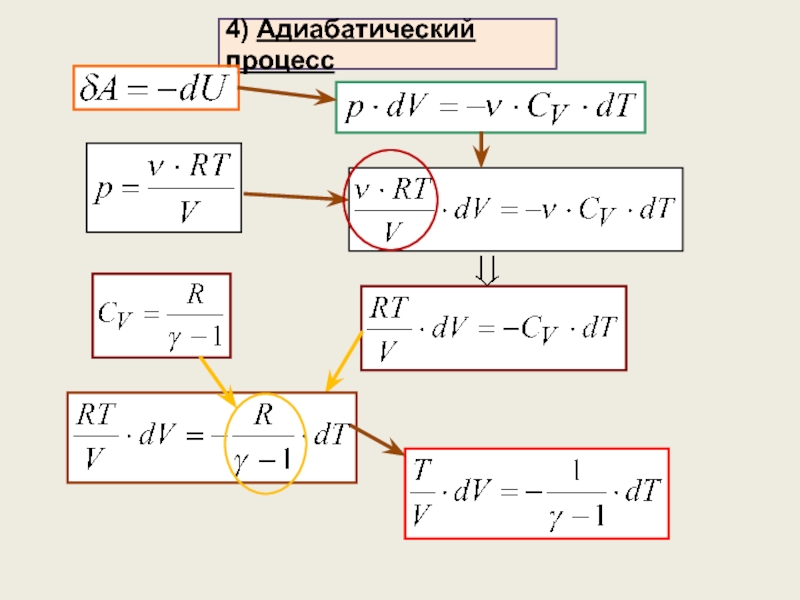
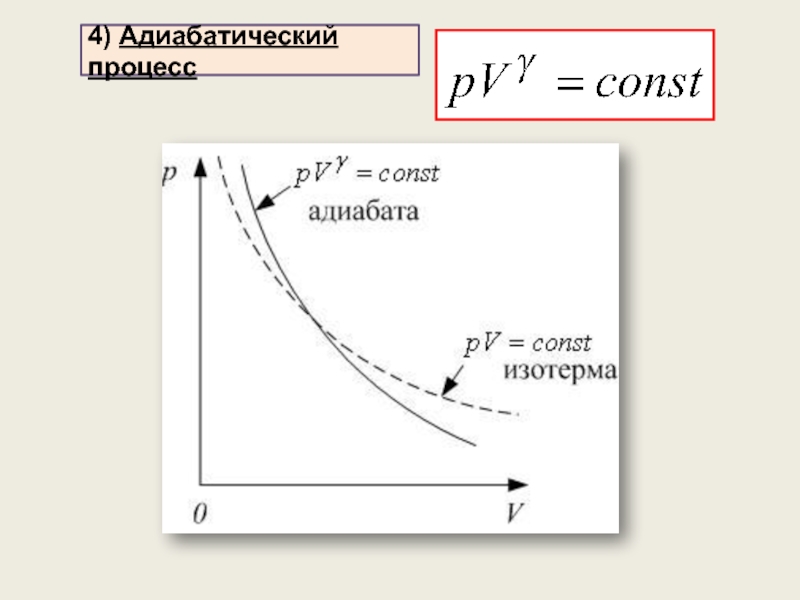
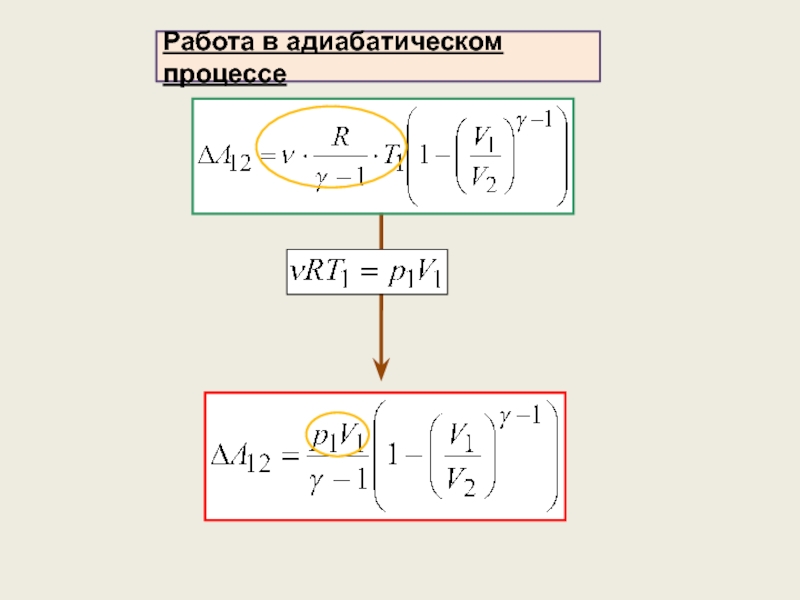
4) Адиабатический процесс (уравнение процесса, график, работа)
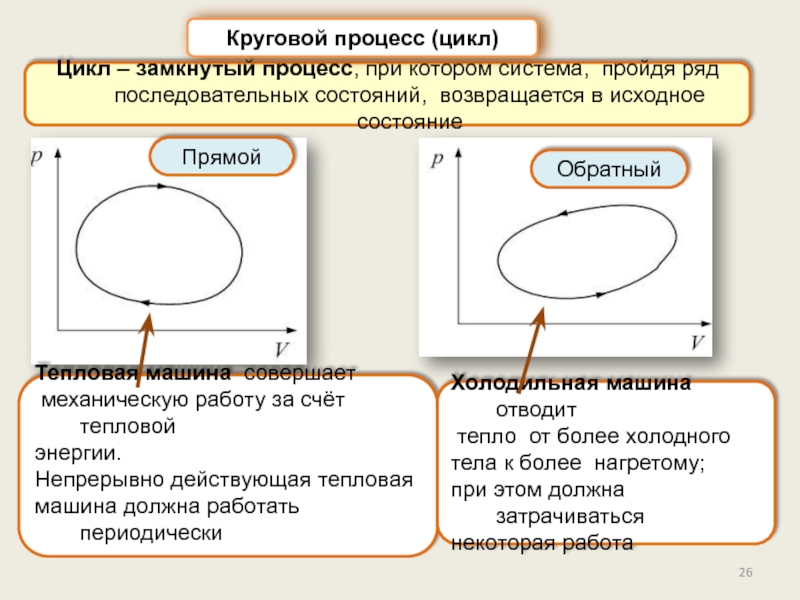
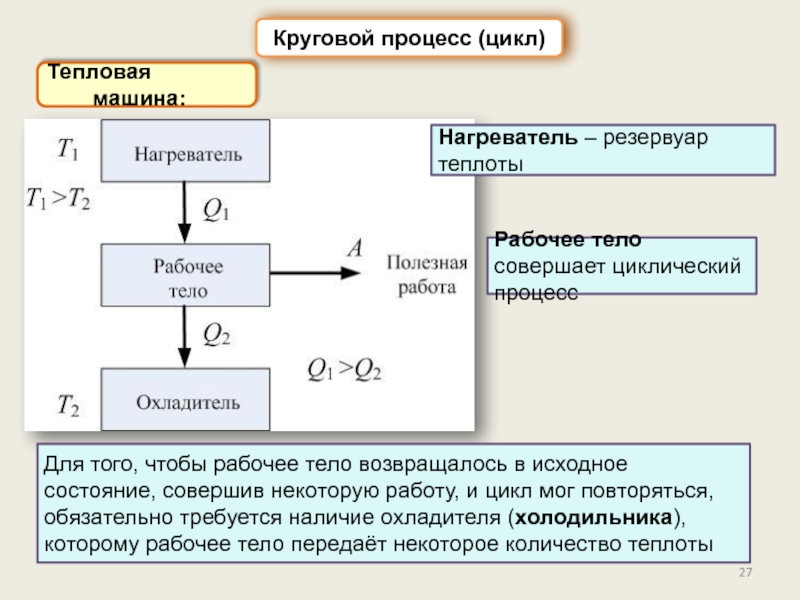
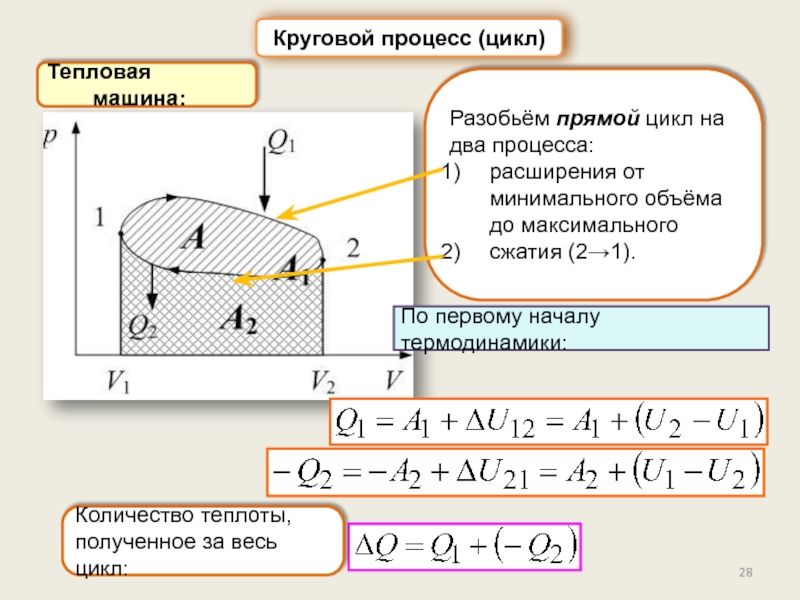
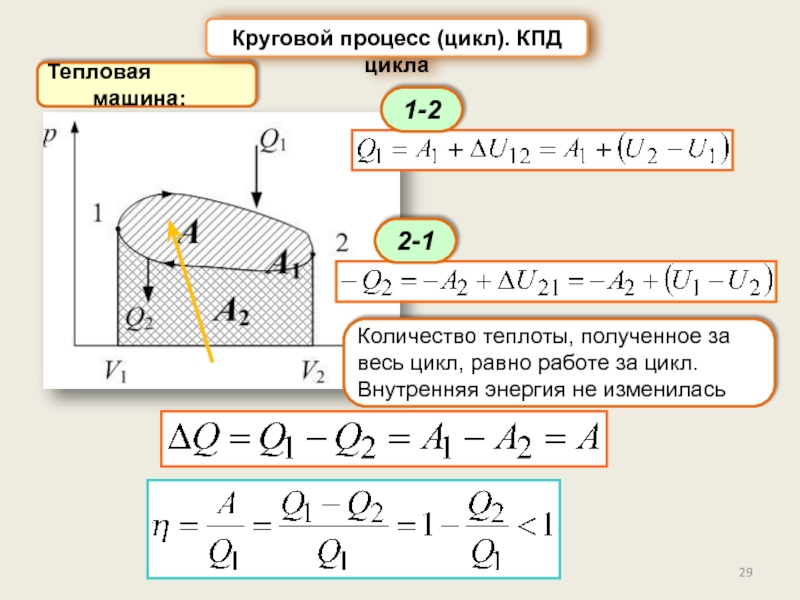
Круговой процесс (цикл). КПД цикла
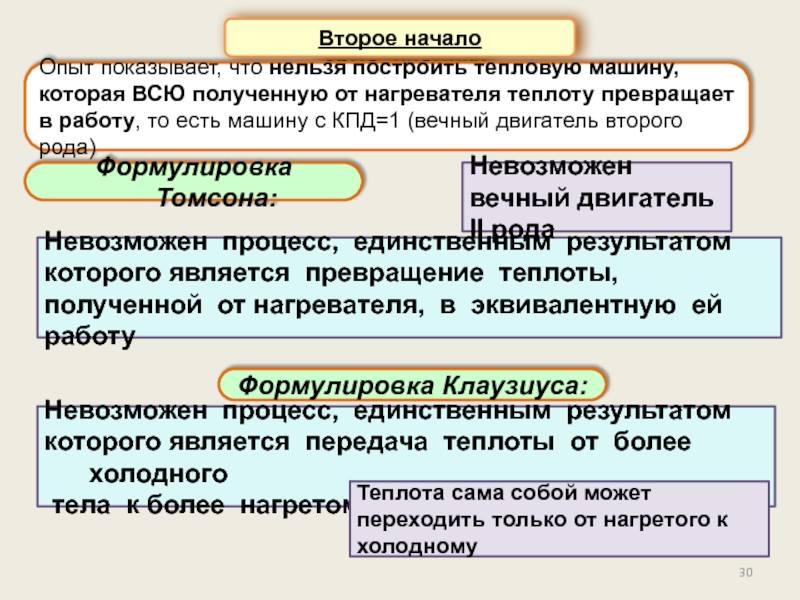
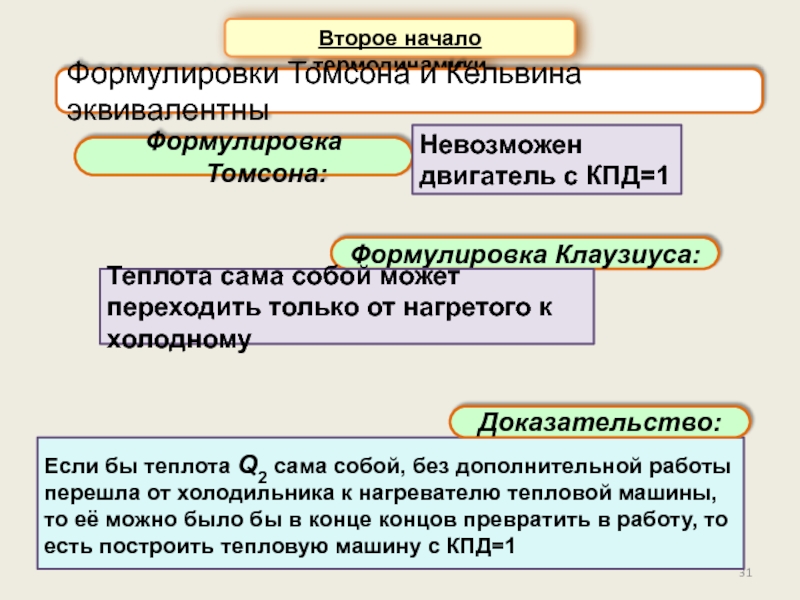
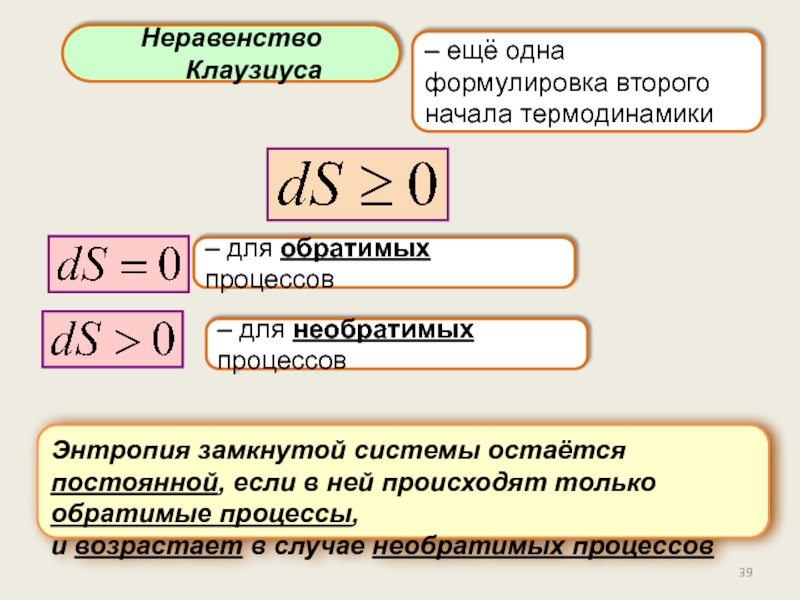
Второе начало термодинамики
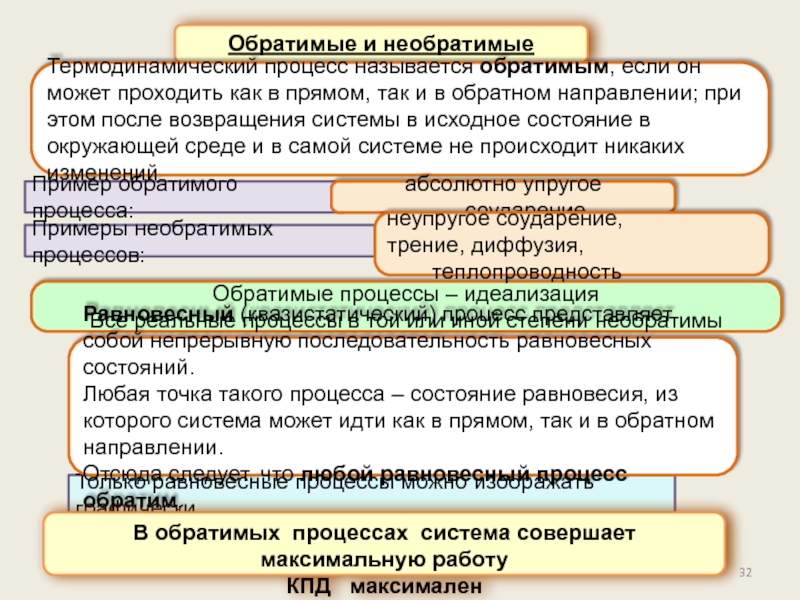
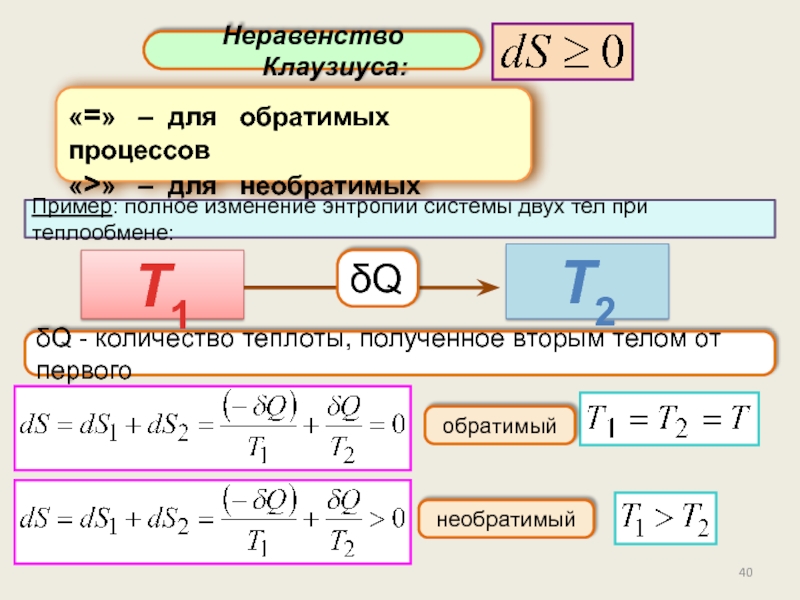
Обратимые и необратимые процессы
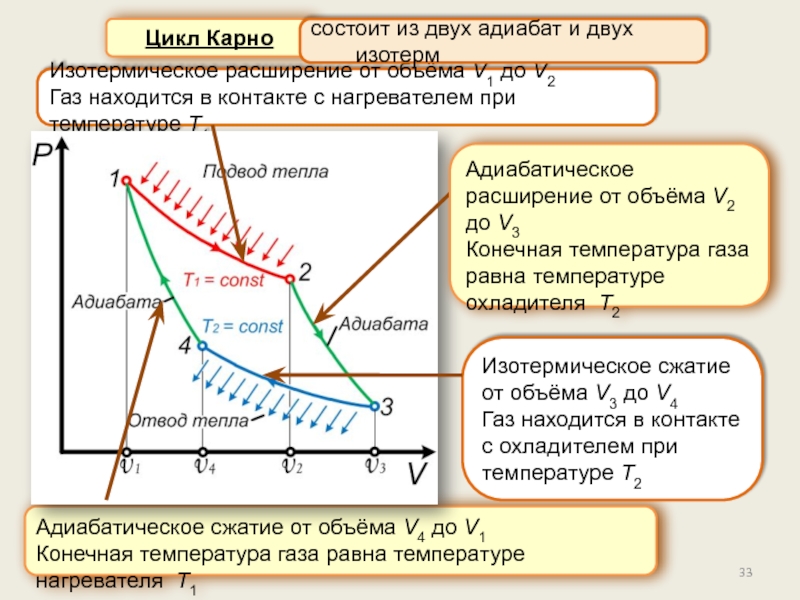
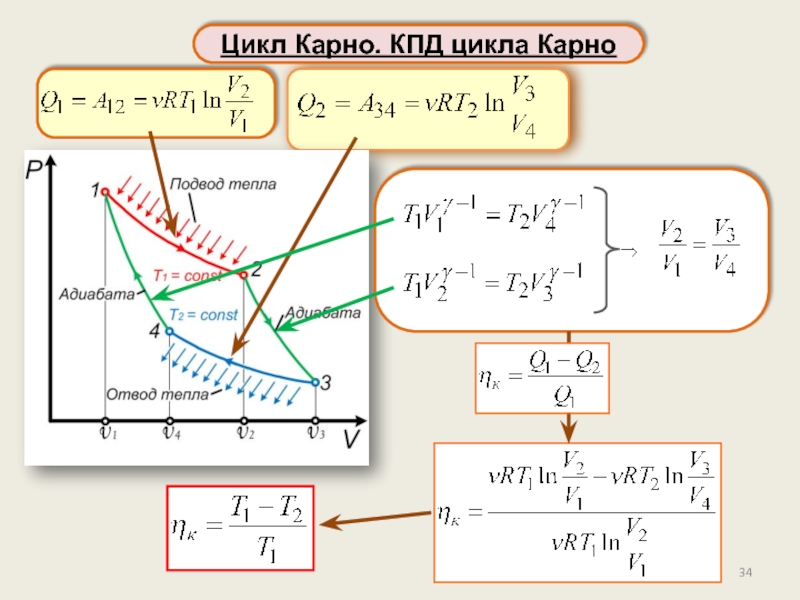
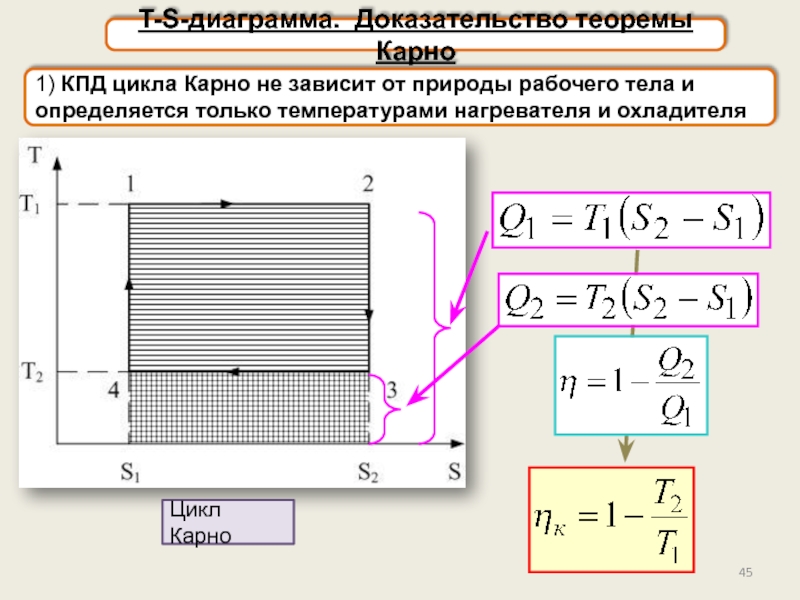
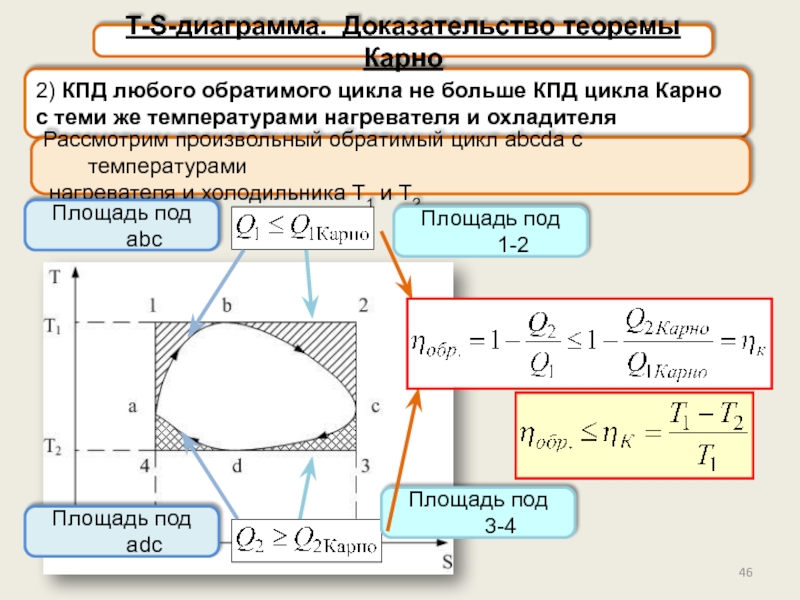
Цикл Карно. Теорема Карно.
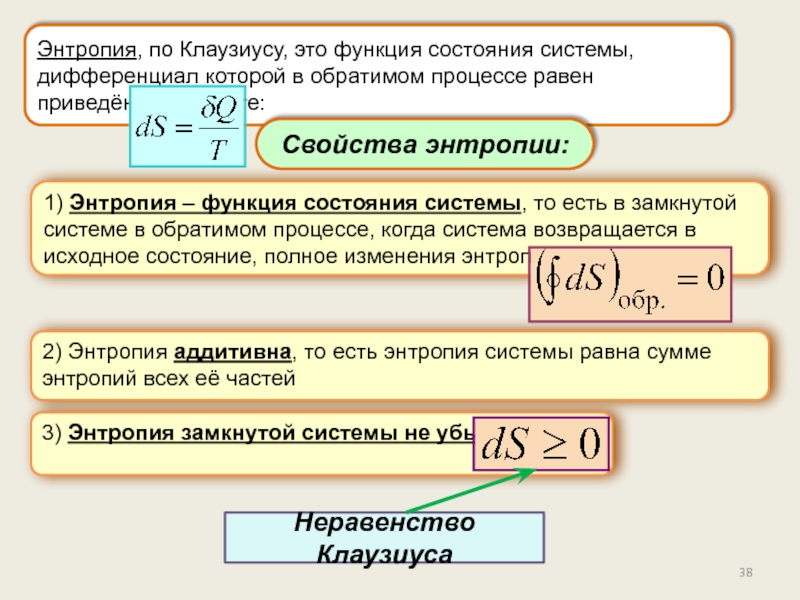
Энтропия.
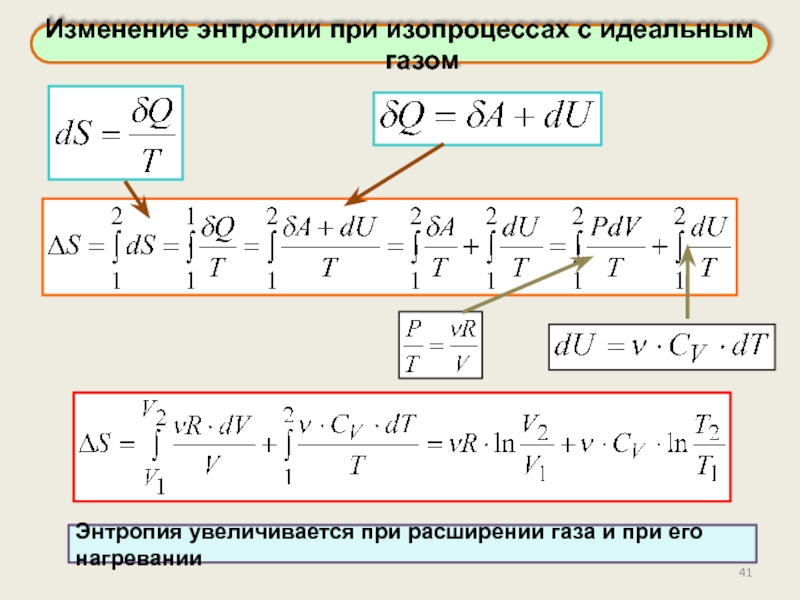
Изменение энтропии при изопроцессах с идеальным газом
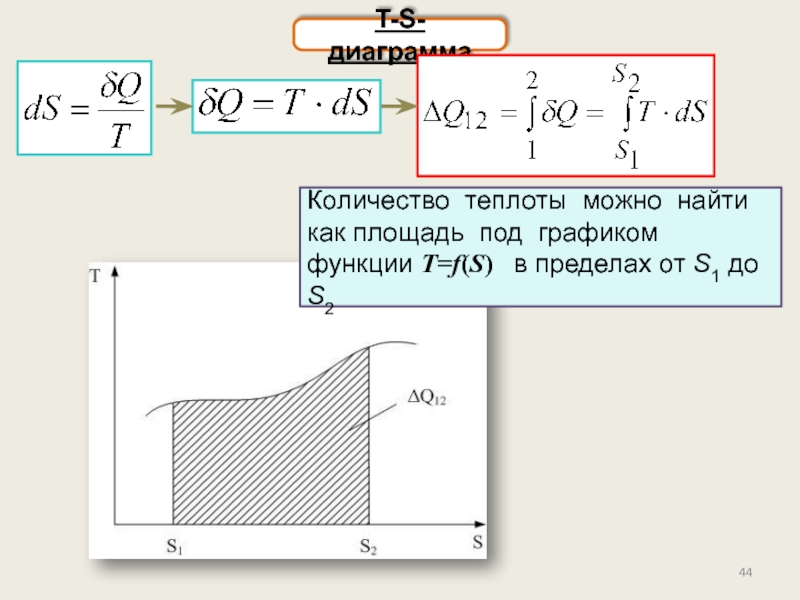
T-S-диаграмма. Доказательство теоремы Карно
Свободная энергия
Энтальпия
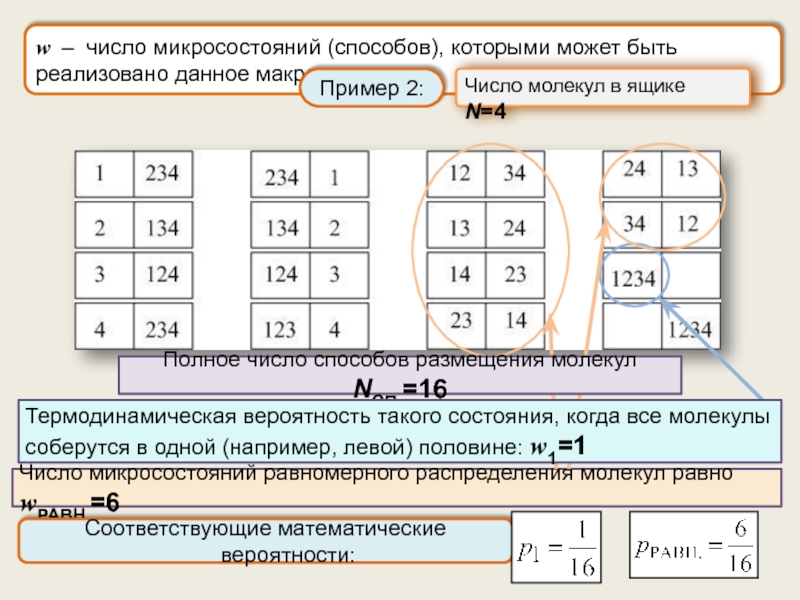
Термодинамическая вероятность состояния системы (статистический вес). Статистический смысл второго начала термодинамики
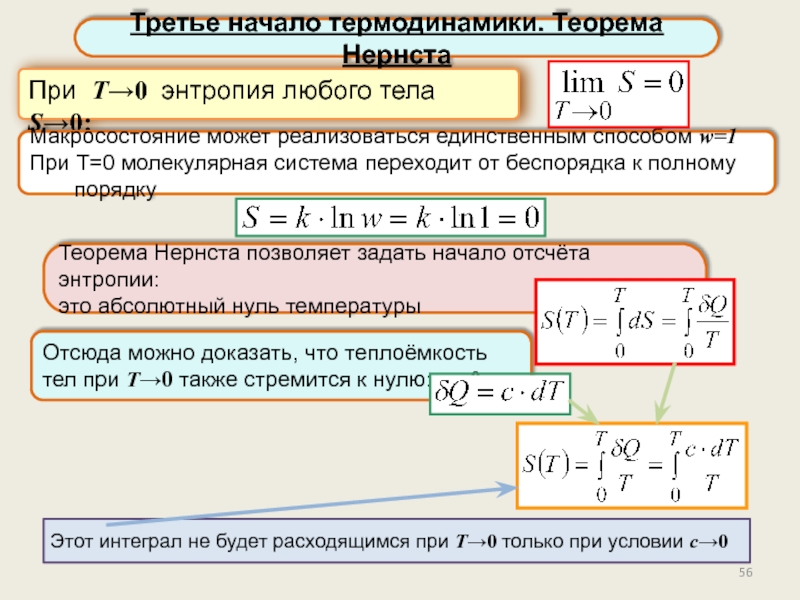
Третье начало термодинамики. Теорема Нернста
Теория тепловой смерти вселенной
Направленность физических процессов (стрела времени)
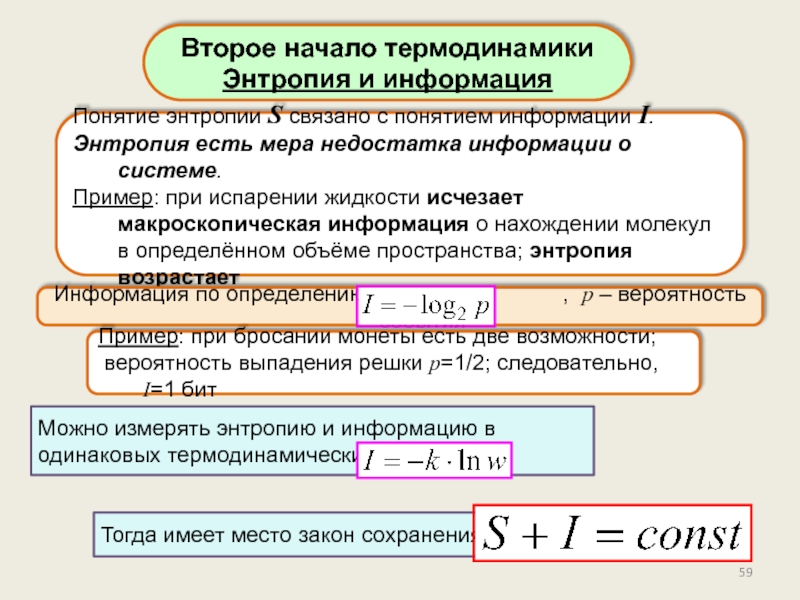
Энтропия и информация
Эволюция открытых систем. Синергетика
План